Perdas Magnéticas - Engenharia Eletrica

1
Perdas Magnéticas
J. V. Filardo, UFPR
Resumo- Este documento permite demonstrar , avaliar e medir
as perdas magnéticas apresentadas em materiais segundo a
norma ASTM
Palavras-chave—Histerese, Foucault, quadro de Epstein, Analisador de potência, materiais magnéticos
que isso também é válido para os átomos de uma estrutura
cristalina. Esses dois elétrons têm spins opostos e, como
cada elétron, quando girando em torno de si mesmo, é equivalente a uma carga se movendo, cada elétron atua como um
magneto extremamente pequeno, com os correspondentes
pólos norte e sul.
I. INTRODUÇÃO
A habilidade de certos materiais - notadamente o ferro, o
níquel, o cobalto e algumas de suas ligas e compostos - de
adquirir um alto e permanente momento magnético, é de
grande importância para a engenharia elétrica. As aplicações
de materiais magnéticos são muitas e fazem uso de quase
todos os aspectos do comportamento magnético.
Existe uma variedade extremamente grande de diferentes
tipos de materiais magnéticos e é importante saber primeiro
porque estes e somente estes materiais possuem propriedades magnéticas e em seguida saber o que leva a comportamento diferentes nestes materiais, por exemplo porque um
material carrega um momento permanente enquanto outros
não.
As pesquisas por materiais magnéticos com melhores características são motivadas pela possibilidade de redução
nas dimensões dos equipamentos e diminuição de limitações
no desempenho devido à saturação e perdas, principalmente
por Histerese e Foucault
II. REVISÃO DE CONCEITOS MAGNÉTICOS
A. Comportamento Magnético
Alguns materiais, tal como o ferro, são marcadamente magnéticos, enquanto que outros não o são. De fato, uma das
técnicas mais simples de separação de materiais ferrosos dos
nãoferrosos é através da comparação de suas propriedades
magnéticas.
A importância histórica e comercial do ferro como um material magnético deu origem ao termo ferromagnetismo, para
englobar as intensas propriedades magnéticas possuídas
pelo grupo do ferro na tabela periódica.
O ferromagnetismo é resultado da estrutura eletrônica dos
átomos. Relembremos que no máximo dois elétrons podem
ocupar cada um dos níveis de energia de um átomo isolado e
J.V. Filardo trabalha na Siemens Ltda e estuda engenharia elétrica
na
Universidade
Federal
do
Paraná
(
e-mail:
[email protected] )
Fig. 2.1 Magnetismo atômico. (a) Diamagnético. (b) Magnético.
De uma maneira geral, em um elemento o número de elétrons que tem um certo spin é igual ao número de elétrons
que tem o spin oposto e o efeito global é uma estrutura magneticamente insensível. Entretanto, em um elemento com
subníveis internos não totalmente preenchidos, o número de
elétrons com spin num sentido é diferente do número de elétrons com spin contrário (Fig 2.1). Dessa forma esses elementos têm um momento magnético global não nulo.
Como os átomos ferromagnéticos adjacentes se alinham
mutuamente, de forma a terem suas orientações numa esma
direção, um cristal ou grão contém domínios magnéticos. Os
domínios geralmente não têm dimensões superiores a 0.05
mm.
Em um material magnético desmagnetizado os domínios
estão orientados ao acaso, de forma que seus efeitos se cancelam. Entretanto, se os domínios são alinhados por um
campo magnético, o material se torna magnético (Fig 2.2). O
alinhamento de todos os domínios em uma direção origina
um efeito aditivo, o qual pode ou não permanecer após a
retirada do campo externo
Fig. 2.2 - Alinhamento de domínios.
2
Um campo magnético externo pode alinhar os domínios ferromagnéticos. Quando os domínios estão alinhados, o material está magnetizado.
Para designar quando o alinhamento magnético é permanentemente retido ou não, são usados respectivamente os
termos “material magnético duro” e “material magnético
mole”; como os materiais mecanicamente duros tendem a ser
magneticamente duros, esses termos são adequados. As
tensões residuais de um material endurecido evitam a redistribuição ao acaso dos domínios. Um material normalmente
perde essa ordenação dos domínios magnéticos quando é
recozido, já que a atividade térmica provoca a desorientação
dos domínios.
III. CURVA DE M AGNETIZAÇÃO E HISTERESE
O processo de magnetização de um material ferromagnético sob a influência de um campo externo se reduz a:
•
crescimento daqueles domínios cujos momentos
magnéticos formam o menor ângulo com a direção do campo,
•
rotação dos momentos magnéticos na direção
do campo externo.
condutor, depende da intensidade da corrente, do comprimento do condutor, da posição deste em relação ao ponto e
de um fator de proporcionalidade µ , que é a permeabilidade
do meio considerado, a equação abaixo:
B = µ. H (3.1)
fornece a relação entre a densidade de fluxo magnético B
(unidade: Tesla) e a força magnetizante H (unidade: A/m).
Para o vácuo a permeabilidade magnética µ = µ 0 é uma constante com o valor 4 ð. 10E-7 no sistema internacional; para o
ar, µ é um pouco maior que µ 0 podendo ser admitida igual a
µ 0 nas aplicações práticas.
No entanto, a permeabilidade magnética µ (unidade: H/m)
não é em geral uma constante, ou seja, B não é uma função
linear de H para algumas substâncias. Portanto, mais importante que o valor da permeabilidade, a representação usual
da relação dada pela Eq. 3.1 é através de curvas B x H.
Estas curvas variam consideravelmente de um material
para outro e para o mesmo material são fortemente influenciadas pelos tratamentos térmicos e mecânicos.
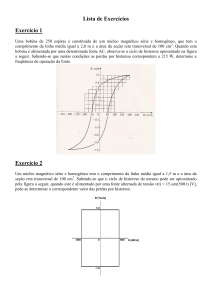
Sua obtenção é feita da seguinte forma: Para um material
inicialmente não magnetizado, ao aumentar progressivamente
a força magnetizante de 0 até Hmax na Fig. 3.3, obtém-se o
ramo 0a'. Reduzindo-se em seguida H de Hmax até zero, temse o ramo a’b’. Quando H = 0, B = 0b’. Para reduzir B a zero, é
necessário aumenta H em sentido contrário até 0c’, obtendose o ramo b’c’ da curva.
Continuando-se a fazer variar H até -Hmax tem-se o ramo
c’d’. Fazendo-se variar H de -Hmax até zero, em seguida até
Hmax e continuando deste modo, obtém-se sucessivamente
os pontos e’- f’ - a’’- b’’ - c’’ - d’’ -e’’ - f’’ - ...
0a' é a curva de magnetização crescente.
Fig. 3.1 - Esquema de orientação dos spins nos domínios.
A saturação magnética se alcança quando acaba o processo de crescimento dos domínios e os momentos magnéticos de todas as regiões imantadas espontaneamente estão
na mesma direção do campo.
Fig. 3.2 - Direções de magnetização fácil, média e difícil
para os cristais de ferro, níquel e cobalto.
Os monocristais das substâncias ferromagnéticas se caracterizam pela sua anisotropia magnética, ou seja a facilidade de magnetização dos cristais variam de acordo com a direção do campo aplicado, como se pode ver na Fig. 3.2 para os
cristais de ferro, níquel e cobalto. O processo de magnetização de um material ferromagnético é caracterizado por suas
curvas de magnetização B x H.
Lembrando que a densidade de fluxo magnético em um
ponto de um campo devido à circulação de corrente em um
Fig. 3.3 - Curva da Magnetização
A densidade de fluxo B = 0b’que permanece quando se
anula a força magnetizante H é o magnetismo remanescente.
Repetindo-se a operação acima descrita (variação de H entre
Hmax e -Hmax) um número suficiente de vezes, obtém-se uma
3
curva fechada que se repete; o material terá então atingido o
estado de magnetização cíclica simétrica (curva abcdefg na
Fig.3.3). A esta curva fechada que se obtém quando o material se acha em estado de magnetização cíclica dá-se o nome
de laço de histerese.
Para um mesmo exemplar de material ferromagnético submetido a ensaio o laço de histerese depende do valor máximo
que se dá à força magnetizante H; a Fig 3.4 apresenta vários
laços de histerese correspondentes a valores máximos diversos de H.
Em qualquer dos laços os valores de B são maiores no
ramo descendente que no ascendente; a substância ferromagnética tende a conservar o seu estado de magnetização,
isto é, tende a se opor às variações de fluxo. Essa propriedade tem o nome de histerese.
A curva na Fig. 3.4, que se obtém ligando os vértices dos
laços de histerese simétricos, correspondentes a uma determinada substância ferromagnético é a curva normal de magnetização; e é geralmente empregada no cálculo de aparelhos
e máquinas elétricas.
IV. FATORES QUE AUMETAM AS PERDAS POR
HISTERESE
•
•
•
Ferro e aço submetidos a tratamento a frio tem as
perdas por histerese aumentadas
Adição de carbono na fabricação do aço aumenta as perdas por hsiterese
Imperfeições ou impurezas dos materiais também
aumentam as perdas.
V. PERDAS POR CORRENTES PARASITAS DE
FOUCAULT
Já as perdas devido as correntes parasitas de Foucault
produzem calor pela ação das correntes (parasitas) que são
induzidas nas chapas de aço silício.
Para melhor explicação deste efeito, será considerado a figura 4, onde está representado a seção de um material magnético qualquer sendo atravessado pelas linhas de força de
fluxo estabelecidas no material.
Pelo fenômeno da indução estudado por Faraday-Lens
será estabelecido correntes na superfície da área de seção do
material magnético, conforme indicado na figura 4.
Fig. 3.4 - Laços de Histerese em Função de Hmax
Figura 4 – Representação das correntes parasitas de Foucault em um material magnético.
Percebe-se que as correntes parasitas induzidas possuem
a liberdade de circular pela superfície do material, sedo limitada apenas pela resistência elétrica do material magnético.
Portanto o quadrado da intensidade das correntes parasitas
multiplicado pela valor da resistência do caminho estabelecido por elas produz calor devido ao efeito Joule. O calor produzido é indesejável. O ideal será eliminar ou mesmo atenuar
a ação deste calor. As perdas por correntes parasitas podem
ser calculadas através da equação 4 abaixo
Onde:
Equação ( 4.0 )
Fig 3.5 – Laço de Histerese visto de um osciloscópio
PF = perdas por eddy-current;
Percebe-se através da análise de (4) que para a redução
das perdas uma das providências necessárias é diminuição
da espessura das chapas. Resultados muito satisfatórios são
4
obtidos submetendo o material aos processos de laminação,
o produto final são finas lâminas de material magnético em de
tal forma a não haver comprometimento nas características
mecânicas exigidas ao material. Outra providência refere-se a
adição de silício na aço provoca um aumento da resistividade do material e consequentemente um aumento da resistência elétrica do material. Uma última providência pode ainda
ser adotada, ou seja realizar a isolação entre as lâminas do
pacote magnético. O resultado desta ação pode ser verificado na figura 5.
material magnético. Como houve adição de silício promoveuse um aumento na resistividade do material. Estes dois fatores substituídos em (4.1) resultam em um aumento da resistência elétrica e conseqüentemente a uma redução significativa nas correntes parasitas e conseqüentemente uma redução quadrática das perdas por correntes de Foucault.
VI. EQUIPAMENTOS PARA DETERMINAÇÃO DE
PERDAS MAGNÉTICAS
A. Quadro de Epstein 25 cm
Aparelho que consiste de 04 solenóides (cada um tendo
duas bobinas) conformando os quatro lados de um circuito
magnético quadrado e um indutor mútuo para compensar o
fluxo disperso destes solenóides. A distância entre os eixos
centrais de cada par de solenóides em oposição é de 25cm ±
0,03 cm. As quatro bobinas internas, ou de potencial, são
ligadas em série de modo a somar as tensões induzidas em
cada solenóide. As bobinas externas, ou de magnetização,
também são ligadas em série de modo a somar a força magnetizante aplicada ao circuito através de uma fonte externa. O
número de espiras primárias é igual ao número de espiras
secundárias, N1=N2. O Quadro Epstein atende a norma
ASTM 343 e é adequado para trabalhar entre 25 e 400 Hz,
N1=N2=700 espiras. O material magnético a ser testado é
colocado no interior dos solenóides na forma de tiras planas
conforme figura 6
B. Analisador de Potência
Figura 5 – Detalhe do material magnético após o processo
de laminação.
A análise matemática dos procedimentos adotados podem
ser analisados através da equação (4.1)
Onde:
Equação (4.1)
RM = resistência elétrica determinado pelo caminho da
corrente;
ñ = resistividade do material magnético;
l = comprimento do material magnético;
S = área da seção do material.
Medidor digital das grandezas potência ativa, reativa e
aparente, além de outras como corrente, tensão, fator de forma de onda, etc. Além das incertezas menores que apresentam estes analisadores digitais, é que permitem realizar medições simultâneas das várias grandezas requeridas, dispensando instrumentação extra.
Para as medições de perdas específicas e separação de
perdas totais em perdas por Histerese e Foucault, os analis adores NORMA, modelo D5255-T e INFRATEK, modelo 305
A são igualmente adequados. Quando é necessário medir
Permeabilidade de pico, este último apresenta a vantagem de
fornecer diretamente o valor de pico da corrente, facilitando a
ajuste da corrente aplicada ao enrolamento de magnetização.
Quando este recurso não é disponível, deve ser empregado um resistor de valor e potência adequados para medir,
indiretamente (pelo método da queda de tensão encima deste
resistor) esta grandeza. Neste caso, o valor de pico da queda
de tensão neste resistor é mais facilmente medida com osciloscópio digital.
Sabe-se que mantendo-se a tensão constante a corrente
permanece constante se não houver variação na resistência
elétrica. Considerando que as correntes produzidas no núcleo do material magnético são devido ao fluxo nele existente
e que ele permanece constante, o único parâmetro que sofrerá variação no processo será a resistência do material. Assim
recorrendo-se a (4.1), percebe-se que para uma diminuição na
espessura do material equivale a uma diminuição da área do
AMOS
FONTE
PRIMÁR
SECUND
~
I
V
QUADRO
Montagem das
5
•
•
Fig. 6. Esquema de ligações pra o ensaio de separação de
perdas
•
VII. DETERMINAÇÃO DO EXPOENTE DE STEINMETZ E
DOS COEFICIENTES DE FOUCAULT E HISTERESE .
•
Existe uma modelagem clássica para materiais magnéticos.
Basicamente, as perdas totais (P) são o somatório das parcelas correspondentes às perdas por Histerese e por correntes parasitas ou de Foucault. Ou:
P = Kh f Bpx + Kf f2 Bp2
Onde x é conhecido como expoente de Steinmetz. Kh e Kf
são os coeficientes de Histerese e Foucault.
Medem-se as perdas totais em três condições. (1) para a
freqüência f1 e a indução de pico Bp1; (2) para a freqüência
f2 e a induçaõ de pico Bp2; (3) para a freqüência f1 e a indução Bp2. Chamando de P1, P2 e P3, respectivamente, a estas
três perdas medidas, temos:
P1 = Kh f1 Bp1x + Kf f12 Bp12 (1)
P2 = Kh f2 Bp2x + Kf f22 Bp22 (2)
P1 = Kh f2 Bp2x + Kf f22 Bp22 (3)
A solução deste sistema de equações fornece os valores
de Kh, Kf e x.


Bp2 ( P2 − a 2 P3 )

log 
 ( P2 − aP3 )Bp1 2 − a( a − 1) P1 Bp2 2 
x=
log( Bp2 / Bp1 )
Kh =
Kf =
P2 − a 2 P3
f 2 (1 − a ) Bp2 x
P2 − aP3
2
f 2 Bp2
2
a
a −1
onde
x= coeficiente de Steinmetz
Kh = coeficiente de Histerese
Kf = coeficiente de Foucault
VIII. REFERÊNCIAS BIBLIOGRAFICAS
ABNT NBR 9025 - Set / 85 “Produtos planos de
aço para fins elétricos, de grão orientado, totalmente processados” - Especificação;
ABNT NBR 5161 - 1977 “Produtos laminados
planos de aço para fins elétricos” - Método de
Ensaio;
ANSI / ASTM A 343 - 69 (Reaprovada em 1974)
“ Standard Test Method for alternating-currente
magnetic properties of materials at power frequencies using wattmeter-ammeter-voltmeter
method and 25-cm Epstein Test Frame”;
Langsdorf, Alexander, S. - “Theory of of Alternating Current Machinery” - MacGraw-Hill, 1955