Capítulo 4 - Difusão

Apoio COTED-CT

Difusão é o transporte de matéria no estado sólido, induzido
por agitação térmica.

Muitas reações e processos industriais importantes no
tratamento de materiais dependem do transporte de massa
de uma espécie sólida, liquida ou gasosa (a nível
microscópico) em outra fase sólida.

Mecanismo pelo qual a matéria é
transportada através da matéria

Os átomos, em gases, líquidos e sólidos,
estão em movimento constante e migram ao
longo do tempo;

Nos metais e ligas metálicas, a difusão dos
átomos é particularmente importante, já que
a maior parte das reações no estado sólido
envolve movimentos atômicos

Processos importantes de difusão
 A galvanização consiste na deposição de Zn sobre
aço, sendo que parte do Zn difunde para o interior do
aço
 A têmpera que consiste em evitar a difusão do
carbono para fora da austenita
 O revenido que consiste em oportunizar saída parcial
do carbono da martensita temperada, visando reduzir
tensões internas

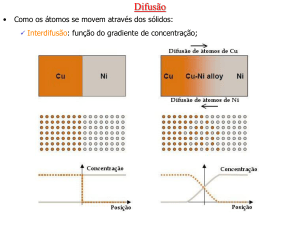
O fenômeno da difusão pode ser demonstrado
mediante o uso de um par de difusão
 Barras de dois metais diferentes, com contato íntimo

Par é aquecido por período prolongado e
resfriado até a temperatura ambiente
 Metais puros nas extremidades separados por uma
região de liga dos dois metais

Interdifusão ou difusão de impurezas



Existe uma tendência do transporte dos
átomos da região de alta concentração para a
região de baixa concentração
A difusão também ocorre nos metais puros,
porém neste caso todos os átomos que estão
mudando de posição são do mesmo tipo;
Autodifusão

Consiste simplesmente na migração passo a
passo dos átomos de uma posição para outra
na rede cristalina.

Os átomos nos materiais sólidos estão em
constante movimento, mudando
rapidamente de posição.

Representações
esquemáticas das
posições atômicas do
Cu e do Ni no interior
do par de difusão.

Concentrações de
cobre e níquel em
função da posição ao
longo do par.

Representações
esquemáticas das
posições atômicas do
Cu e do Ni no interior
do par de difusão.

Concentrações de
cobre e níquel em
função da posição ao
longo do par.

Um mecanismo envolve a troca de um átomo
de uma posição normal da rede para uma
posição adjacente a vaga ou lacuna na rede
cristalina.

O segundo tipo de difusão envolve átomos
que migram de uma posição intersticial
vizinha que esteja vazia. Esse mecanismo é
encontrado para a interdifusão de impurezas
tais como hidrogênio, carbono, nitrogênio e
oxigênio.



O regime estacionário obedece a
primeira lei de FICK;
A difusão é um processo que depende
do tempo (t);
O objetivo de saber o tempo, é saber a
rapidez que ocorre a difusão – taxa de
transferência;

expressa como fluxo
difusional (j), o qual é definido como
a massa (m) que se difunde em uma
seção transversal de área (A)
unitária do sólido por unidade de
tempo (t).
A
taxa
é
J= m/At > unidade kg/m².s ou átomos/m².s


Nesse regime o fluxo difusional não
varia com o tempo;
Um exemplo clássico é a difusão dos
átomos de um gás através de uma placa
metálica,
na
qual
as
concentrações/pressões de componente
em difusão sobre ambas as superfícies
das placas são mantidas constantes.
Figura 1: Difusão: www.feng.pucrs.br/~schroeder/Ciência%20dos%20Materiais/Difusão.ppt

Quando uma concentração “C” é
representada em função da posição ou da
distância no interior de um sólido (x), a
curva resultante é denominada perfil de
concentração e a inclinação em um ponto
particular sobre essa curva é o gradiente
de concentração.
Gradiente de concentração: dC/dx
Gradiente de concentração: ∆C/ ∆x= (Ca – Cb) /
(Xa- Xb)

Primeira lei de Fick:
Onde D é o coeficiente de difusão expresso m2
/ s. O sinal negativo indica que a direção de
difusão é contrária ao gradiente.
 Quando a difusão ocorre, de acordo com a
equação, o gradiente de concentração é a
força motriz.

Difusão em estado não estacionário
A maioria das situações práticas envolvendo difusão, ocorre
em condições de estado não estacionário.
O fluxo de difusão e o gradiente de concentração em um
ponto específico no interior de um sólido, variam ao longo
do tempo.
A figura abaixo mostra o perfil de concentração em 3
momentos diferentes do processo de difusão.
Sob condições de regime não estacionario, usa-se a equação
diferencial parcial, conhecida por segunda lei de Fick:
Se o coeficiente de difusão é independente da
composição e portanto da posição x (o que deve ser
verificado para cada caso específico) ai a equação anterior
fica:
Hipóteses a serem adotadas:
1- Antes do início da difusão os átomos do soluto em difusão
que estejam presentes no material estão uniformemente
distribuídos mantendo uma concentração Co;
2- O valor de x na superfície é zero e aumenta com a
distância para dentro do sólido;
3- O tempo zero é tomado como sendo o instante
imediatamente anterior ao início do processo de difusão.
Essas condições de contorno são representadas pelas
expressões:
As aplicações das condições de contorno acima na
segunda lei de Fick fornece a solução:
Onde Cx fornece a concentração em uma profundidade
x após decorrido um tempo t .
O termo a direita é a função erro de Gauss cujos valores
são dados em tabelas matemáticas. Uma lista parcial
aparece no próximo slide:
A solução para a segunda lei de Fick demonstra a relação que
existe entre a concentração, posição e o tempo, qual seja que
Cx, sendo uma função do parâmetro adimensional
pode ser determinado em qualquer tempo e em qualquer
posição, bastando para tanto que os parâmetros Co, Cs e D
sejam conhecidos.
Suponha que se deseje atingir uma determinada concentração
de soluto C1 em uma liga, o lado esquerdo da equação se
torna então:
Logo o lado direito da equação
também é uma constante
e subsequentemente:
Exemplo 01
Em um processo de cementação em um aço com 0.25 % de carbono a 950ºC
com uma concentração de carbono na superfície externa de 1.2% , qual deve ser o
tempo de cementação para atingir um teor de carbono de 0.8% na posição de 0.5
mm abaixo da superfície? O coeficiente de difusão do carbono no ferro nessa
temperatura é de
Solução: Problema de difusão no estado não estacionário sendo a
composição da superfície mantida constante . As condições de contorno do
problema são as seguintes:
Necessitamos determinar agora o valor de z cuja função erro é
0.4210. Deve-se usar uma interpolação:
Exemplo 02
O coeficiente de difusão do cobre no alumínio a 500ºC e 600ºC são
respectivamente 4,8 X10-14 e de 5.3 X 10-13 m2/s . Determine o tempo
aproximado a 500ºC que produzirá o mesmo resultado de difusão em termos
de concentração de cobre em um ponto específico no alumínio equivalente a
10 h de tratamento térmico a 600ºC
Solução:
Na mesma posição teremos a mesma concentração de cobre logo x é
constante assim:

Uma tecnologia que se aplica a difusão em estado
sólido é a fabricação de circuitos integrados (CI)
semicondutores.

Monocristais de silício são o material básico para a
maioria dos CI. Para que esses dispositivos CI
funcionem satisfatoriamente, concentrações muito
precisas de uma impureza (ou impurezas) devem ser
incorporadas em minúsculas regiões espaciais no
chip de silício, e uma maneira de se fazer isso é por
meio de difusão atômica.

Os dois tratamentos térmicos considerados para a difusão
de impurezas no silício durante a fabricação de circuitos
integrados são a pré-deposição e a redistribuição.

Durante a pré-deposição, os átomos de impureza são
difundidos para o interior do silício, frequentemente a
partir de uma fase gasosa, cuja pressão parcial é mantida
constante.

Na etapa de redistribuição, os átomos de impureza são
transportados mais para o interior do silício, de forma a
gerar uma distribuição de concentrações mais adequada,
porém sem aumentar o teor global de impurezas.
Problema-exemplo 5.6 (Callister, 2012)
Difusão do Boro no Silício
Átomos de boro devem difundir em uma pastilha de
silício usando ambos tratamentos térmicos de prédeposição e de redistribuição; sabe-se que a
concentração de fundo do B nessa pastilha de silício é de
1X1020 átomos/m3.
Problema-exemplo 5.6 (Callister, 2012)
Difusão do Boro no Silício
O tratamento de pré-deposição deve ser conduzido a
900oC durante 30 minutos; a concentração de B na
superfície deve ser mantida em um nível constante de
3X1026 átomos/m3. A difusão de redistribuição será
o
conduzida a 1100 C por um período de 2h. Para o
coeficiente de difusão do B no Si, os valores de Qd e D0
são 3,87 e V/átomo e 1X10-3m2/s, respectivamente.
Lista de símbolos
Símbolo
Significado
A
Área da seção transversal perpendicular à direção da difusão
C
Concentração do componente em difusão
C0
Concentração inicial do componente em difusão antes do início do
processo de difusão
Cs
Concentração superficial do componente em difusão
Cx
Concentração na posição x após um tempo de difusão t
D
Coeficiente de difusão
D0
Constante independente da temperatura
M
Massa do material em difusão
Qd
Energia de ativação para difusão
R
Constante dos gases (8,31 J/mol.K)
t
Tempo decorrido no processo de difusão
x
Coordenada de posição (ou distância) medida a direção da difusão,
normalmente a partir de uma superfície sólida





A magnitude do coeficiente de
difusão é um indicativo da taxa
segundo a qual os átomos se
difundem.
As espécies difusivas, bem como
seu
material
hospedeiro,
influenciam o coeficiente de
difusão.


A temperature tem a influência mais
marcante sobre os coeficientes e
taxas de difusão.
A dependência dos coeficientes de
difusão em relação à temperature
de dá pela equação:


A energia de ativação pode ser
considerada como a energia
necessária
para
produzir
o
movimento difusivo de um mol de
átomos.
Energia de ativação elevada resulta
em um coeficiente de difusão
pequeno.
A
constante pré-exponencial e a
energia de ativação do Fe em
cobalto são dados. Em qual
temperature o coeficiente de
difusão terá o valor de 2.1×10----ˉ¹
m²/s?
D0 = 1,1× 10ˉ⁵m²/s
Qd = 253300 J/mol
 RESPOSTA: T = 1518,0 K
 Quanto
maior a energia de ativação,
menor é a velocidade do processo e
maior a sensibilidade da velocidade
com a temperatura.
 A energia de ativação depende do tipo
de átomo, estrutura e do mecanismo.
 Geralmente a energia para uma
difusão por lacuna é maior que a
energia da difusão intersticial.
 Os
coeficientes de difusão se
modificam com os caminhos de
difusão disponíveis no material.
 Geralmente a difusão ocorre mais
facilmente em regiões estruturais
menos restritivas.
 A difusão ocorre mais rapidamente
em materiais policristalinos do que
em monocritais.
A EQUAÇÃO DE ARRHENIUS
A
temperatura tem uma grande influência sobre os
coeficientes e as taxas de difusão (CALLISTER, 2011);
A velocidade da maioria das reações químicas aumenta à
medida que a temperatura também aumenta (CINÉTICA...,
2010);
A
equação de Arrhenius, foi proposta pelo químico sueco
Svante August Arrhenius, onde a qual expressa a
dependência da constante de velocidade (k) com a
temperatura (PERUZZO e CANTO, 2012).
x
Coeficiente
angular
(b) linear
Coeficiente
y(a)
Figura 01- Gráfico de Arrhenius.
GRÁFICO DE ARRHENIUS
D0 conhecido como fator “pré-exponencial”, ele está
relacionado à frequência das colisões, mas também inclui
orientação e outros fatores (RAMOS e MENDES, 2005);
Qd é a energia de ativação. Representa a “barreira” de
energia que deve ser vencida antes que os reagentes se
tornem produtos; e é sempre positivo. Quanto maior o valor
de Qd ,menor a velocidade de uma reação a uma dada
temperatura, e maior será a inclinação da curva (ln k) x (1/T).
Uma energia de ativação alta corresponde a uma velocidade
de reação que é muito sensível á temperatura. O valor de Qd
não muda com a temperatura (RAMOS e MENDES, 2005);
GRÁFICO DE ARRHENIUS
Já
uma pequena energia de ativação indica uma velocidade de
reação que varia apenas ligeiramente com a temperatura (a
curva de Arrhenius tem uma inclinação pequena) (PERUZZO e
CANTO, 2012).
E
uma reação com energia de ativação nula, como para certas
reações de recombinação de radicais em fase gasosa, tem uma
velocidade que é virtualmente independente da temperatura
(PERUZZO e CANTO, 2012).
GRÁFICO DE ARRHENIUS
Qd
Qd
Qd
Figura 02- Gráfico de Arrhenius
– Energia de ativação –
inclinação da reta.
Fonte: CINÉTICA..., 2010.
 TABELA DE DADOS DE DIFUSÃO
Fonte: CALLISTER, 2011.
 GRÁFICO DO LOGARÍTIMO DO COEFICIENTE DE DIFUSÃO
VERSUS O INVERSO DA TEMPERATURA PARA VÁRIOS METAIS:
Fonte: CALLISTER, 2011
Quando o fluxo de difusão e o gradiente de
concentração em um ponto específico no interior de
um sólido, variam com o tempo.
Segunda lei de Fick.
Se o coeficiente de difusão é independente da
composição e portanto da posição x ai a equação
anterior fica:
FONTE: CALLISTER e RETHWISCH, 2012
Na prática, para um sólido considerado semi-infinito, em que a concentração na
superfície é mantida constante.
Dessa forma as seguintes hipóteses são adotadas:
1- Antes do início da difusão os átomos do soluto em difusão que estejam presentes
no material estão uniformemente distribuídos mantendo uma concentração Co .
2- O valor de x na superfície é zero e aumenta com a distância para dentro do sólido.
3- O tempo zero é tomado como sendo o instante imediatamente anterior ao início
do processo de difusão.
Essas condições de contorno são representadas pelas expressões:
FONTE: CALLISTER e RETHWISCH, 2012.
As aplicações das condições de contorno acima na
segunda lei de Fick fornece a solução:
Onde Cx fornece a concentração em uma
profundidade x após decorrido um tempo t .
O termo a direita é a função erro de Gauss cujos
valores são dados em tabelas matemáticas.
FONTE: CALLISTER e RETHWISCH, 2012.
A função
é a integral normalizada de probabilidade ou função de erro de
Gauss. A função de erro de Gauss é definida como:
Em que
é a variável z. Os valores da função de erro de
Gauss z=erf(y), são tabulados.
FONTE: LMDMWISCH, 2005.
FONTE: CALLISTER e RETHWISCH, 201
Aplicando-se a Equação
é possível avaliar quantitativamente a informação da Figura a
seguir num gráfico padrão único.
FONTE: LMDMWISCH, 2005.
FONTE: LMDMWISCH, 2005.
FONTE: LMDMWISCH, 2005.
FONTE: LMDMWISCH, 2005.
A importância da curva mostrada está na inter-relação
existente entre a distância, o tempo, o coeficiente de difusão e
a concentração, durante a difusão.
FONTE: LMDMWISCH, 2005.

FONTE: LMDMWISCH, 2005.
Para se produzir uma determinada concentração numa certa região de um material,
ou para se conseguir difundir para dentro do material uma certa fração da
quantidade necessária à saturação total, é necessário apenas manter o mesmo valor
de
em que L é uma dimensão que caracteriza o tamanho do objeto.
A Figura apresenta um exemplo de aço cementado. Uma barra de aço com 0,24%p
de carbono inicial foi aquecida a 870°C na presença de carbono em excesso.
FONTE: LMDMWISCH, 2005.
Solução:
Difusão no estado não estacionário
sendo a composição da superfície
mantida constante . As condições de
contorno são:
Determinar o valor de z cuja função erro
é 0.4210. Interpolando:
Então
FONTE: CALLISTER e RETHWISCH, 2012.
REFERÊCIAS
CALLISTER, William, D. Ciência e Engenharia de Materiais – Uma
introdução. 7ª ed. Rio de Janeiro: LTC, 2011.
CINÉTICA Química equação de Arrhenius. Material didático. 2010.
Disponível em:
<http://www.quimica.ufpb.br/monitoria/Disciplinas/Cinetica_quimica/material
/Cinetica_Quimica_Aula_4.pdf>. Acesso em abril de 2014.
PERUZZO, Francisco, M.; CANTO, Eduardo, L. Química na abordagem
do cotidiano. 4ª ed. São Paulo: Moderna, 2012.
RAMOS, Bruno; MENDES, Wendel, T. Parâmetros de Arrhenius: Efeito
da Temperatura na Velocidade de uma Reação. Trabalho acadêmico.
Anápolis, 2005. Disponível
em:<http://www.geocities.ws/ramos.bruno/academic/arrhenius.pdf>.
Acesso em: abril de 2014.
http://www.dem.uem.br/cleber/wpcontent/uploads/2010/03/Capitulo-5.pdf
 http://www.foz.unioeste.br/~lamat/downmateriais/materiais
cap8.pdf
 LMDM - Laboratório de Material Didático. Ciência dos
materiais – Multimídia. Centro Tecnológico de Minas
Gerais (CETEC). 2005. Disponível em:
<http://www.cienciadosmateriais.org/index.php?acao
=exibir&ca p=19&top=299>. Acesso em 03 de abril de 2014.
