Física A - Sistema de Ensino Energia

GABARITO
Física A – Extensivo – V. 7
Exercícios
01)B
Ocorre violação do princípio da conservação da energia.
Eperdida = EPI – EPII
Eperdida = m . g . hI – m . g . hII
Eperdida = 0,65 . 10 . 1,8 – 0,65 . 10 . 1,4
Eperdida = 2,6 J
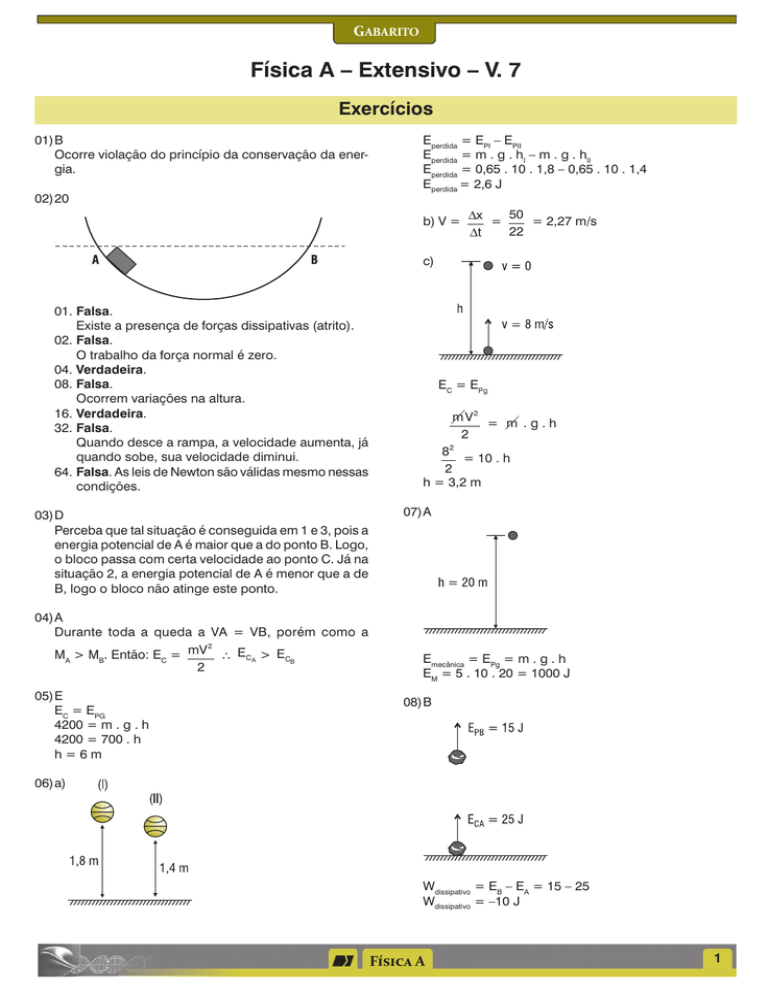
02)20
b)V =
50
∆x
=
= 2,27 m/s
22
∆t
c)
01.Falsa.
Existe a presença de forças dissipativas (atrito).
02.Falsa.
O trabalho da força normal é zero.
04. Verdadeira.
08.Falsa.
Ocorrem variações na altura.
16.Verdadeira.
32.Falsa.
Quando desce a rampa, a velocidade aumenta, já
quando sobe, sua velocidade diminui.
64.Falsa. As leis de Newton são válidas mesmo nessas
condições.
EC = EPg
82
= 10 . h
2
h = 3,2 m
07)A
03)D
Perceba que tal situação é conseguida em 1 e 3, pois a
energia potencial de A é maior que a do ponto B. Logo,
o bloco passa com certa velocidade ao ponto C. Já na
situação 2, a energia potencial de A é menor que a de
B, logo o bloco não atinge este ponto.
04)A
Durante toda a queda a VA = VB, porém como a
2
MA > MB. Então: EC = mV ∴ ECA > ECB
2
05)E
EC = EPG
4200 = m . g . h
4200 = 700 . h
h=6m
m V2
= m .g.h
2
Emecânica = EPg = m . g . h
EM = 5 . 10 . 20 = 1000 J
08)B
06)a)
Wdissipativo = EB – EA = 15 – 25
Wdissipativo = –10 J
Física A
GABARITO
Wfat = fat . d . cos 180o
– 0,5 = fat . 0,1 . (–1)
fat = 5 N
09)I. Falsa.
À medida que a altura diminui a velocidade aumenta.
II. Verdadeira.
III. Falsa.
A velocidade aumenta.
IV. Verdadeira.
c)Na posição 0 cm, temos:
EPEL = EC + Wfat
mV 2
Kx 2
=
+ Wfat
2
2
10)EMA = EM
B
ECA + EPg = EC
B
2,5 . 103 + 2 . 102 =
0, 01 . V 2
+ 0,5
2
0, 01 V 2
1,5 – 0,5 =
2
1
.
2
2
=V
0, 01
mVB 2
2
6 VB 2
∴ VB2 = 900 ∴ VB = 30 m/s
2
2700 =
V=
11)B
Em = EC + EPg + EP
Em = mV
2
+m.g.h+
Kx
2
2
200 = 10 2 m/s
2
2
EMA = EPel = Kx = 400 . 0, 2 = 8 J
2
2
EM = 80% . EMA = 80% . 8 = 6,4 J
Wfat = 6 . 4 – 8 = – 1,6 J
2
200 . 22
Em = 60 . 3 + 60 . 10 . 15 +
2
2
Em = 270 + 9000 + 400
Em = 9670 J
B
01. Falsa.
EM = EPg
B
12)D
EC = EP
6,4 - m . g . h ∴ 6,4 = 0,5 . 10 . h ∴ h = 1,28 m
02.Verdadeira.
04.Verdadeira.
08.Verdadeira.
EMA > EM
B
elástica
2
mV 2 = Kx
2
2
4 . 102
10000 . x 2
=
2
2
x=
=
14)46
elástica
2
300 . ( 0,1)
2
2
16.Falsa.
Wpeso = – ∆εPg
32.Verdadeira.
64.Falsa.
Ocorre dissipação de energia.
400
10000
x = 20 = 0,2 m ou 20 cm
100
15)E
13)a)x = 10 cm = 0,1 m
F = K . x = 300 . 0,1 = 30 N
EMA = EM
B
EPEL = EPg
Kx 2
=m.g.h
2
4 . 102 . ( 0,1)
= 0,5 . 10 . h
2
h = 0,4 m
2
b)
Física A
GABARITO
16)C
08.Verdadeira.
FR = FEL – P ∴ FR = KX – mg
FR = 500 . 0,1 – 2 . 10
FR = 30 N
16.Verdadeira.
EPgA = EMB
EMA = EM
B
EPEL = EPg
Kx 2
=m.g.h
2
500 . x 2
= 0,25 . 10 . 1
2
x = 0,1 m ou 10 cm
32.Verdadeira.
64. Falsa.
18)E
17)60
Obs.: VB = VMIM =
EMA = EM
B
gR
ECA = ECB + EPg
B
m VB 2
m VA 2
=
+ m .g.h
2
2
Vo 2 = 5 gR
2
2
Vo =
EMA = EM
B
EPg = EPEL + ECB
19)A
mV 2
Kx 2
+
m.g.h=
2
2
2V 2
500 . 0,12
2 . 10 . 0,3 =
+
2
2
6 – 2,5 = V2
V = 3, 5 m/s
01.Falsa.
V = 3, 5 m/s
02.Falsa.
EPgA = EPel + E
CB
B
04.Verdadeira.
5 gR
A V0
h
h
4
EMB = EMA
EPg B + ECB = EPgA + ECA
B
m . V0 2
m . g . h + ECB = m . g . h +
2
4
2
m
.
V
0
ECB = 3 m . g . h +
2
4
Física A
GABARITO
20)20
V2
g . 2 .  + 2 g = g(1,6) + D
2
2
VD2 = 2,8 g .  ∴ VD = 2, 8 g
04. Verdadeira.
08.Falsa.
EMA = EMD + Edissipada
EPA + E = E + E + E
CA
PD
CD
dissipada
em D . vD = 0
m . g . 2 + m . 2 . g = m . g (1,6) + Edissipada
2
Edissipada = 1,4 g
EMA = EM
C
m VA
2
m . g . hA +
g.2.+
(
2 g
2
)
2
2
=
16. Verdadeira.
Quando o pêndulo para em C, toda a energia de A
será perdida.
Como no ponto A a energia é:
2
EMA = m . g . h A + m . VA =
2
m
.
2
.
g

m . g . 2 + 2
EMA = 3 m . g 
2
C
mV
2
2
= V.c
2
2
2 g .  + g  = V . c ∴ VC2 = 6 g
2
Quando parar em C, essa energia representará o
trabalho do atrito.
21)A
hD

sen 37o =
HD = 0,6
HD =  + 0,6 = 1,6
01.Falsa.
No ponto C, temos:
FCP = T – P
m . VC 2 = T – m . g
2
mVC2
+m.g
T=
2
m . 6g
+m.g
T=
2
T = 7 m . g = 7P
02.Falsa.
EMA = EMD
EPA + E = E + E
CA
PD
CD
m . g . hA +
ECA = EP
G
B
m VA 2 = m . g . h
2
2
V2
=g.h∴h= V
2
2.g
22)B
2
m VA 2
= m . g . h + m VD
2
2
EPA = EPEL
m . g .h =
Física A
B
Kx 2
2
2
m . gR = Kx
2
m . g2R
K
2mgR
x=
K
x2 =
GABARITO
23)18
EMB = 72 %. EM
EMB = 72 . EMA
100
EMB = 72 . m . g . h
100
m VB 2 = 72 . m . 10 . 40
100
2
VB2 = 576
VB = 24 m/s
V = 24 x 3,6
V = 86,4 Km/h
01. Falsa.
02.Verdadeira.
04.Falsa.
08.Falsa.
16.Verdadeira.
32.Falsa.
64.Falsa.
EMA = EM
B
25)B
26)A
Através do gráfico, no fim da aceleração,
temos:
V = 12,5 m/s
Q = m . v = 90 . 12,5 = 1125 Kg . m/s
2
m V2 = m V ’ + m . g . h
2
2
V ’2
V2
– g . h =
(x2)
2
2
V2 – 2 . g . h = V' 2
V' = V 2 − 2 . g . h
27)D
I. Verdadeira.
t = 3s ∴ v = 15 m/s
2
2 . 152
Ec = m . v =
= 225 J
2
2
II. Verdadeira.
Entre t = 3 s e t = 5 s, a velocidade é
constante, portanto Fr = 0
III. Falsa.
Pois ∆V ≠ 0, logo ∆Q ≠ 0
IV. Verdadeira.
W = ∆εC = EC – ECO = 225 – 0 = 225 J
∆tA = ∆tB
d
d’
=
v
v’
 d
 
v
2


d’
= 

2
 V − 2 . g . h
2
d2 =
d ’2
2
2
V
V −2.g.h
d' =
d2 −
28)B
(Falsa). Impulso é uma grandeza vetorial,
podendo ser gerado ou não por uma força
instantânea.
(Verdadeira)
(Verdadeira)


(Falsa) I = ∆Q
d2 . 2 . g . h
V 2
24)A
V=0
29)B
o
I = ∆Q = mV – m Vo = 0,25 . 30 = 7,5 N . S.
30)A
Sistema isolado.
31)47
Com air bag ou sem air bag


∆QC = ∆QS
No entanto,
c/ air bag:
s/ air bag:
Física A
GABARITO
01. Verdadeira.
02.Verdadeira.
Sim, pois a variação da velocidade é a mesma.
04.Verdadeira.
Teorema do impulso.
08.Verdadeira.

∆Q é a mesma nas duas situações.
16.Falsa.
As massas dos corpos são diferentes.
Q=m.V
32. Verdadeira.
64.Falsa.


F com air bag < F sem air bag
2
a) EC = m . Vo = 0, 06 . 1 = 0,03 J
D
2
2
b)W = ∆εC = EC – EC = 0 – 0,03 = – 0,03 J
O
c)F = m . a
3 = 0,06 . a ∴ a = 50 m/s2
d)V2 = Vo2 + 2 . a . d
02 = 12 + 2 . (–50) . d
100 d = 1 ∴ d = 1 = 1 cm
100
1
∆
v
e)a =
∴ 50 =
∴ ∆t = 0,025
∆t
∆t
37)D
32)E


I = ∆Q
36)D
Quem variou mais a quantidade do movimento obteve
o maior impulso, logo alcançou a maior altura.
33)15
01.Verdadeira.
I = ∆Q
0
I = Q – Qo
0
I = ∆Q = Q – Q o
F . ∆t = m . V
F . 0,01 = 0,4 . 25
F = 1000 N
I=Q
F.t=m.v
F . 0,01 = 0,058 . 50
F = 290 N
02.Verdadeira.
Pois formam um par ação-reação
04. Verdadeira.
I=F.t
I = 290 . 0,01 = 2,9 N . S
08.Verdadeira.
Teorema do impulso.
16.Falsa.
Fexterna = 290 N
32.Falsa.
O > impulsos são iguais em módulo.
38)28 N
34)A
I = ∆Q
EPA = ECB
0
I = Q – Qo
I=m.v
I = 0,03 . 20
I = 0,6 N . S
m .g.h=
10 . 3,2 =
V2 = 64
V = 8 m/s
35)A
v0
m V2
2
V2
2
v=0
02 = VB2 – 2 . 10 . 1,8
– VB’2 = –36
fat
VB’ = 6 m/s
I = ∆Q
I = Q – Qo
I = – m . Vo
I = – 0,4 . 10
I = –4 N . S
I = ∆Q
I = m VB’ – mVB
o
VC2 = Vo2B + 2 . a . ∆x
F . t = 0,5 . 6 – 0,5 . (–8)
F . 0,25 = 3 + 4 ∴ F = 28 N
Física A
GABARITO
39)D
41)E
I = Q – Qo
I = 2 . 10 . –2 . 2
I = 16 N . S
W=F.d
m . V 2 m . Vo 2
W=
–
2
2
2 . 102
2 . 22
W=
–
2
2
W = 96 J
o
Ipeso = Q – Qo
42)A


I = ∆Q
Ipeso = –2 . 20
Ipeso = – 40 N.S.
I = QF – Q0
F . t = mVf – mV0
F . 0,03 = 0,3 . (–20) – 0,3 . 30
F = – 500 N
40)A
43)C
I.Verdadeira.
Sen θ =
h
h’
=
L
L’
h = � . sen θ

h' = � '. sen θ
EPg = EC
2
m . y . L . sen θ = mV
2
I = Área = ∆Q
I=6.N.S
∴ V =
Assim, a sua velocidade aumenta até
o instante 2 s.
2 . g . L . senθ
II. Verdadeira
F (N)
EPg = EP’ + E’C
g
m . g . L . sen θ = m . g . L' . sen θ +
m  V
 
2  2
2
m . g . L. sen θ = m . g . L' . sen θ + m V
8
2 . gL . senθ
g . L . senθ = g . L ’ . senθ +
8
L = L' + 2L
8
L' = – 2L + L
8
3
L' = L
4
Logo, x é 1 L
4
3
I1 = 6 N . S
1
7
0
2
4
2
t (s)
–2
Física A
I2 = Área2 = – 2 . 3 = – 6 . N . S
Itotal = I1 + I2 = 0
GABARITO
III.
IV.
44)
Falsa.
FR = 0 ∴ a = 0 ∴ v = CTE
Falsa.
No instante 7 s a velocidade do automóvel se anula,
porém continua havendo a atuação de uma força.
F (N)
Logo,
∆Q = 0
Assim:
Qfinal = Q0 = m . Vo
50 = 10 . Vo
Vo = 5 m/s
45)A
46)A
100
A
t (s)
5
a)Vo = 5 m/s
Qo = m . Vo =10 . 5 = 50 Kg . m/s
I = ∆Q = Área = (b + B ) h = ( 2 + 5 ) . 100
2
2
I = 350 kg . m/s
Qtotal = QO + ∆Q
Qtotal = 50 + 350 = 400 Kg . m/s
b)t = 7,5 s ∴ F = – 70 N
F = m . a ∴ – 70 = 10 . a ∴ a = – 7 m/s2
c)5 m/s.
A força cessa em t = 10 s
I = Área = I1 + I2
I = 350 – 350 = 0
A1 = I1 = 350 N . S
onde: Q1 > Q2
Logo: V1 > V2 e
F (N)
V3 = V4
47)09
Antes
100
P
A1 = I1 = 350 N.S
1
0
v
10,0
5,0
t (s)
Depois
01. Verdadeira.
2
08.Verdadeira.
–70
A2 = I2 = b . h
I2 = – 70 . 5
I2 = – 350 N . S
Física A
As demais alternativas não possuíram um vetor
resultante após a explosão horizontal para a
direita.
GABARITO
48)E
50)
–e
nêutron
+e
x
Q=0
carga do nêutron = 0
pois Qdepois = 0
já a carga dessa partícula:
0 = +e – e + x
x=0
49)E


a) Q antes = Q depois
Logo:


Q0= Q1
mVo = m1V1
m V0 = m . V1
6
V1 = 6V0


Q antes = Q depois




Q 0 = Q 3+ Q 1+ Q



Q 3 + Q 2 = QR3,2

QR3,2 =
Como:
m = m1 + m2 + m3
m
m = m1 +
+ m
2
3
m1 = m
6
2
b)Q3 = Q2
m3V3 = m2V2
m
m . V3 =
V2
2
3
Q23 + Q22 + 2Q3 . Q2 . cos 120o

QR3,2 =
1
2
(mV3 ) + (mV2 )2 + 2 . mV3 .mV2  − 2 

QR3,2 =
(m . 0, 4)2 + (m . 0, 4)2 + 2 . m . 0, 4 . m . 0, 4 .  −

QR3,2 = 0,4 m
m . 3V = m .V
0
2
2
3
V2 = 2V0
1

2
c)Início
Assim,


Q1 + ( Q 2 + Q 3) = 0,8 m + 0,4 m = 1,2 m
Emo = Eco =
m . Vo 2
2
Fim
Em = EC1 + E2 + EC3
f
Dessa forma:
Q0 = Qfim =
M0 . V0 = 1,2 m
3 m V0 = 1,2 m
2
2
mV22
Em = mV1 =+
+ mV3
2
2
2
2
2
m
2
m
(6Vo ) + 2 (2V0 ) + m3 ( 3Vo )
Em = 6
.2
.2
.2
22
2
2
Em =
m Vo = 11 mVo (aumenta)
2
V0 = 0,4 Km/h
Física A
GABARITO
51)06
01.Falsa.
No barco com metade da massa teremos o dobro
da velocidade.
02.
Q0 = Qf
0 = QA + QB ∴ 0 = mA . VA + mB . VB
–2 m . VA = m . VB ∴ – 2VA = VB
04.
08.Falsa.
16.Falsa.
As velocidades de A e B poderiam ser escritas na
seguinte forma.
VB = 2V
VA = V
2M. V 2 = MV2
EC A =
2
M(2V )
= 2MV2
2
2
ECB =
Em relação à parede d = 6 cm
54)D
Arma frouxamente


Q0 = Q fim
O = Qrifle + Qprojétil
O = mR . VR + mP . VP
–5 . VR = 0,015 . 3 . 102
VR = 0,9 m/s
52)17
01.Sistema isolado.
02.Falsa.
Possuem sentidos opostos.
04.Falsa.
A massa do sapo 1 é maior que a massa do sapo
2, logo a força que o primeiro sapo faz para se
impulsionar é maior. Desse modo, a rampa se
desloca enquanto os sapos estão no ar para a
esquerda.
08.Falsa.
Como o sistema é isolado, as quantidades de
movimento do sapo 1 e 2 são iguais em módulo.
Assim, o sapo que possui menor massa possuirá
maior velocidade de lançamento e, por consequência, maior alcance.
dsapo 2 > dsapo 1
16.As forças aplicadas no início para colocarem os
sapos e as tábuas em movimento são novamente
aplicadas no final, agora parando todo o sistema.
Arma firmemente


Q 0 = Q fim
O = Qprojétil + Qatirador+arma
O = mA . VA + mT . VT
(95 + 15) VA = 0,015 . 3 . 102
VA = 0,045
VA = 4,5 . 10–2 m/s
55)C
Qo = Qfim
O = Qcanhão + Qprojétil
– Qcanhão = Qprojétil
– 150 . V2 = 1,5 . 150
V2 = 1,5 m/s
56)C
53)E
Qo = Qfim ∴ O = Qformiga + Qlâmina
10
– Qformiga = Qlâmina
– m . VF = m VL
5
VL = – VF
5
Ou seja, a formiga tem uma velocidade 5 vezes maior do
que da lâmina. Assim, enquanto a lâmina anda 1 cm, a
formiga anda 5 cm.
Física A
Q1 + Q2 = Qconjunto
m . 3,5 + m . 1,5 = 2 m . V
V = 2,5 m/s
GABARITO
57)D


Q 0 = Q fim
O = Q1 + Q2
O = m1 . V1 + m2 . V2
– 4 . 100 = 80 . V2 ∴ V2 = –5 m/s
Vrelativo = 5 + 4 = 9 m/s
58)B
Qantes = Qdepois
0
QA + Q B = QAB
mA . VA = (mA + mB) . V
4 . 1 = (1 + 4) . V
V = 0,8 m/s
Qantes = Qdepois
Qbarro = Q(barro + carro)
2 . 4 = (2 + 6) . V'
V = 1 m/s
62)14
01.Falsa.
Q0 = Qf
O = Q1 + Q2
– 2 . V1 = 4 . V2
V1 = –2V2
02.
04.Forças internas (sistema isolado) não alteram a
posição do centro de massa.
08.Ação/reação
16.Falsa.
Sistema conservativo, a energia mecânica se conserva.
63)86
59)C
Qantes = Qdepois
Qantes = mA . VA + mB . VB
Qantes = 4 . 104 . 1 + 3 . 104 . 0,5
Qantes = 5,5 . 104 Kg . m/s
60)A
Qantes = Qdepois
M . V =  M + M  . V'


3
M . V = 4 M . V'
3
3
.V
V' =
4
61)B
Qo = mV = 10 m


Q final = Q inicial = 10 m
01.Falsa.
Qdepois = Q1 + Q2 =
02.Verdadeira.
Qdepois = Q1 + 0 =
04.Verdadeira.
Física A
m
m
. V1 =
. 20 = 10 m
2
2
Qdepois = Q1 + Q2 =
08.Falsa.
Qdepois = Q1 –
m
m
. 15 +
(–5) = 5 m
2
2
m
m
. 30 +
. (–10) = 10 m
2
2
m
. 25 = 12,5 m
2
11
GABARITO
66)A
16.Verdadeira.
m
Qdepois = Q1 + Q2 =
. 25 +
2
32. Falsa.
m
Qdepois = Q1 =
. 10 = 5 m
2
64.Verdadeira.
m
Qdepois = Q1 + Q2 =
. 50 +
2
m
. (–5) = 10 m
2
A
v
antes
v/2
m
. (–30) = 10 m
2
v
depois
v
2
64)C
Se admitirmos que, em ambos os casos, temos
o mesmo fenômeno apenas visto por dois observadores inerciais diferentes, podemos fazer
uma resolução bastante simples.
2,5
t
Situação 1
(m)
v2
v1
2
1
2.m
3
m
3
Situação 2
Quantidade de movimento antes
PA = m . v = m . v
PB = 0
Quantidade de movimento depois
v
v
PA + PB = m .
+m.
=m.v
2
2
⇒ A quantidade de movimento se conserva!
2
Ecinética antes = m . V
2
2
2
 V
 V
m 
m 
m . V2
Ecinética depois = E’CA + E’ =  2  +  2  =
CB
4
2
2
⇒ A energia cinética não se conservou.
67)B
P e l o g r á f i c o p e r c e b e m o s q u e a p ó s a c o l i s ã o
V1 – V2 = 0, ou seja, possuem a mesma velocidade, não se
afastam; colisão inelástica.
Na situação (2) devemos somar vetorialmente.
65)C
fação em módulo é igual a freação.
68)23
01.Verdadeira.
Forças externas são nulas, então o sistema é isolado.
02.Verdadeira.

Q antes = 0 (repouso)
04.Verdadeira.


Q antes = Q depois
12
Física A
GABARITO
08.Falsa.
Como a massa do astronauta é dez vezes
maior que a massa do tanque, então se a
velocidade do tanque ao ser arremessado
for de 5 m/s, a de recuo do astronauta será
de 0,5 m/s.
16.Qantes = Qdepois
Qtanque = Qtanque + astronauta
10 . 5 = (10 + 90) . V
V = 0,5 m/s
69)B
70)B
EPA = ECA
2
V2
m . g . h = m V ∴ 10 . 0,45 =
∴ V = 3 m/s
2
2
71)C


Q antes = Q depois
mbola . Vbola = mbloco . Vbloco + mbola . Vbola
2 . 3 = 10 . Vbloco + 2 Vbola
'
'
6 = 10 Vbloco
+ 2 Vbola
(1)
como e = 1
V
− Vbola
∴ 1 = Vbloco − Vbola
e = bloco
3
3
V'bloco – V''bola = 3
(2)
Resolvendo o sistema formado pelas equações 1 e 2, temos:
V'bloco = 1 m/s
V''bola = – 2 m/s
72)E
I) Antes
2 . 42
= 16 J
2
2
ECB = 4 . 2 = 8 J ⇒ ECtotal = 24 J
2
Depois
2.2 2
= 4,5 J
EC A =
2
2
ECB = 4 . 3 = 18 J ⇒ E’ctotal = 22,5 J
2
Correto. Será uma colisão parcialmente elástica.
II) Antes
Vrelativa A/B = 6 m/s
Depois
Vrelativa A/B = 5 m/s
V . af
e = rel
= 5
Vrel . ap
6
Como 0 < e < 1, é parcialmente elástica.
III) Falsa.

Q antes
EC A =
Qantes = Qdepois
70 . 6 = (70 + 50) . V'
V' = 3,5 m/s
73)D


Q antes = Q depois
Qantes = QA + QB
Qantes = 2 . 4 + 4 . (–2) = 0
m . V = 2 m . V'
V' = 2 m/s
Qdepois = colisão inelástica, os corpos seguem
juntos após a colisão.
Qdepois = (mA + mB) . V
= (2 + 4) . 8 = 6 8 Kg . m/s


Perceba que Q
≠ Q depois, logo essa situantes
EC = EP
m V2
= m .g.h
2
22 = 10 . h ∴ h = 0,2 m
2
h = 20 cm
ação é incorreta.
Física A
13
GABARITO
74)21
01.Verdadeira.
Velocidade é relativa.
02.Falsa.
mV 2
EC =
2
04.Verdadeira.
08.Falsa.
Em qualquer sistema isolado ocorre conservação da quantidade de movimento.
16.Verdadeira.
 m1 . 2 . g . d 
 m+m

2

1
2
X= V = 
2g
2g
X=d.
 m1 
 m + m 
1
2
m21 . 2 g . d
2
=
(m1+ m2 )2
2g
2
77)C
Antes
75)B
Antes
Depois
2
ECantes = 2 . 10 + 4 . 82 = 100 + 128 = 228 J
2
2
Depois
Qantes = Qdepois
0,4 . 10 = (0,4 + 0,6 ) . V'
V' = 4 m/s
Qantes = Qdepois
2 . 10 + 4 .(–8) = (2 + 4) . V
V = 2m/s
2
ECdepois = 6 . 2 = 12 J
2
Houve uma perda de 216 J.
• ECantes =
• ECdepois
m1 . V12
0, 4 . 102
=
= 20 J
2
2
2
2
= (m1 + m2 ) . V = ( 0, 4 + 0, 6 ) . 4 = 8 J
2
2
Houve uma perda de 12 J.
76)x = d . [m1/(m1+m2)]2
78)B
Antes
Antes do choque
ECA = EP
m V12 = m . g . d ∴ V1 =
2
2.g.d
Depois do choque
Movimento da batida
Qdepois = Qantes
(m1 + m2) . V = m1 . V1
m1 . V1
V=
m1 + m2
Determinação de X:
I) Verdadeira.
EC = EP
Qantes = QB = mB . VB ∴ como mB =
Qantes =
Como Qantes = Qdepois =
(m + m ) . V
1
2
2
14
2
(
)
= m1 + m2 . g . X
Física A
mA
. VB
2
mA
. VB
2
mA
2
GABARITO
2
m
II) ECantes = ECB = mB . VB = A . ( 2VA )
2
2
2
= mA . VA2
2
ECdepois = EC
A
=
2
A
= mA . V
2
Logo, houve uma perda.
2
2
mA . VA2 = mA . VA = mA . VA
2
2
III) A quantidade de movimento foi conservada.
 m 
M . V1 + (m + M) . V ∴ V = 
. V1
 m + M 
EC = (m + M) . V
=
2
=
(m + M) .
M2
(m + M)2
2
. V12
=
m2 . V12
(m + M) . 2
64.Verdadeira.
81)Antes
79)a)E M início = m . g . h
EM = m . g . h
fim
Eabsorvida = m . g . H – m . g . h =mg . (H – h)
b)EP = EC
m . g . h =
V=
Depois
2 m/s
( )
2 2
mV 2
=
2
2
Qantes = Qdepois
2 . 2 = 4 . Vm
V2
Vm =
m/s
2
Assim:
EC =
m V2
V2
∴ 10 . 0,1 =
∴
2
2
2
=2J
 2
4

mVm2
 2 
ECM =
=
2
2
Eabsorvido = 2 . 1 = 1 J
a)
2
=
4.
2
2
4 =1J
80)86
01.Falsa.
Ao se alojar, a velocidade do projétil em relação ao bloco é nula, mas o sistema está em
movimento, portanto, a energia cinética e a
quantidade de movimento não serão nulas.
02.Verdadeira. Quanto maior a velocidade do
projétil, maior será a altura atingida.
04.Verdadeira.
Em uma colisão perfeitamente inelástica
ocorre perda de energia cinética.
08.Falsa.
O sistema é isolado.
16.Verdadeira.
Ecinética_projétil + bloco = EPotencial_projétil + bloco
32.Falsa.
mV12
ECO =
2
Qantes = Qdepois
N = P = m . g = 8 . 10 = 80 N
fat = µ . N = 0,4 . 80 = 32 N
FR = m . a
32 = 8 . a ∴
b)Wfat = Edissipada = fat . d = 32 . 13,5 = 432 J
c)Análise da colisão
Qantes = Qdepois
Q1 = Q(1+2)
8 . 12 = (8 + 8) . V ∴ V = 6 m/s
em 1 caixa → fat = 32 N
em 2 caixas → fat = 64 N
Fa = m . a
64 = 16 . a ∴ a = 4 m/s2
Física A
15
GABARITO
V2 = Vo2 + 2 . a . d
O2 = 62 + 2(–4) . d
d = 4,5 m
02.Verdadeira.


Q inicial = Q fim
Q8 = m . V8
82)a)
30º
60º
Qbranca = m . 5
FR = m . a = m . ∆V = 70 . −25
∆t
0,1
FR = –17.500 N
b)v0 = 20 m/s
FR = fat
m .a=µ.m .g
a = 0,610 ∴
V2 = Vo2 + 2 . a . d
102 = 202 + 2(–6) . d
12 d = 400 – 100 ∴ d = 300 = 25 m
12
QB' = m . vB'
v = 10 m/s
c)Colisão perfeitamente elástica (juntos)
Qantes = Qdepois
1200 . 30 = (1200 + 1800) . V
V = 12 m/s.
83)90
’
’
1
Sen 30o = m VB ∴
= VB ∴ VB = 2,5 m/s
2
5
m.5
04.Falsa.
A colisão é perfeitamente elástica, ocorre portanto conservação da energia.
08.Verdadeira.
Se a quantidade de movimento no início não possui componente vertical, no fim também não haverá.
2
16.Falsa. EC = m . 5 = 25 m
O
2
2
Com base no triângulo formado na alternativa 02: 3
cos 30o = m V8 ∴
= V8 V8 = 2,5 3 m/s
2
5
m5
E
’
C8
2
)
2
= 3,125
3 m
32. Falsa.
Justamente o contrário, a energia cinética total antes é igual
à energia cinética total depois da colisão.
64.Verdadeira.
84)e = (3 .
01.Falsa.
O sistema é isolado.
16
=
(
m . 2, 5 3
Física A
2 +2.
3 )/12 ≅ 0,64