ESCOAMENTOS EM REGIME TRANSIENTE

ESCOAMENTOS EM REGIME TRANSIENTE
 Regime transiente: são escoamentos que apresentam
variação com o tempo ⇒ ∂/∂t ≠ 0
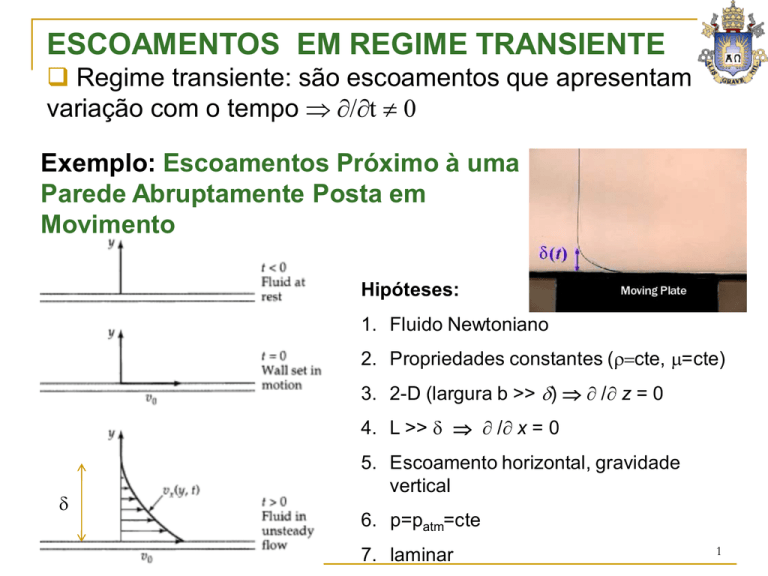
Exemplo: Escoamentos Próximo à uma
Parede Abruptamente Posta em
Movimento
Hipóteses:
1. Fluido Newtoniano
2. Propriedades constantes (ρ=cte, µ=cte)
3. 2-D (largura b >> δ) ⇒ ∂ /∂ z = 0
4. L >> δ ⇒ ∂ /∂ x = 0
δ
5. Escoamento horizontal, gravidade
vertical
6. p=patm=cte
7. laminar
1


∂ρ
+ ∇ • ( ρ V ) = 0 ⇒ ρ = cte ⇒ ∇ • V = 0
∂t
Continuidade:
∂u ∂v ∂w
+
+
= 0 ⇒ v = cte
∂x
∂y 
∂z

0 ( 5)
Condição de contorno: y=0 ; v=0
0 ( 4)


V = u( y, t ) i
v=0



D
V
2
Q.M.L. (Navier-Stokes): ρ
= ρ g −∇ p+ µ∇ V
Dt
Q. M. L - direção z e y satisfeitas de acordo com as hipótese listadas
Q. M. L - direção x
∂p
∂u
∂u
∂u
∂u
∂ 2u ∂ 2u ∂ 2u
ρ( + u
+ v
+ w ) = ρgx −
+µ( 2 + 2 + 2 )
 ∂x
∂t 
∂x 
∂y
∂z
∂x
∂y 
∂z



0(5) 
0( 4)
0( v =0)
∂ u
∂ 2u
=υ
∂t
∂ y2
υ = viscosidade
cinemática; υ = µ/ρ (m2/s)
0(3)
0( 6)
0( 4)
0(3)
Condição inicial
Condições de contorno, t >0
1) t ≤ 0 ; u =0
1) y=0; u =uo
para ∀ y
2) y→ ∞ ; u=0
2
Adimensionalizando
a velocidade
u
U=
uo
∂ U
∂ 2U
=υ
∂t
∂ y2
Espera-se que a medida que o tempo passa, δ cresce, mas a forma do perfil
mantenha-se similar. Então é conveniente adimensionalisar a coordenada
vertical com a espessura de penetração δ, tal que U= U(y/δ)
η
=
y
δ
Podemos estimar a variação da espessura de penetração δ com o tempo,
analisando a equação de momentum
∂ u
∂ 2u
=υ
∂t
∂ y2
U ≈υ U
t
δ2
η=
⇒ δ ~ υt
y
4υ t
o número 4 é introduzido por conveniência, como será visto no resultado final
Mudança de variáveis: U= U(η, τ) onde η = y/(4 υ t)0.5
e
τ=t
4
U= U(η, τ) onde η = y/(4 υ t)0.5
e
τ=t
Para introduzir a mudança de variáveis na equação de conservação, é preciso
utilizar a regra da cadeia
∂U ∂ η ∂U ∂ τ
∂ U
=
+
∂η ∂ y
∂τ ∂ y
∂y
∂U ∂ U ∂η ∂ U ∂τ
=
+
∂t
∂ η ∂t
∂ τ ∂t
mas
∂ η
=
∂t
1η
y
3/ 2
−
1
=−
( − )t
2
2 t
4υ
∂η
=
∂y
η
1
=
4υ t
y
∂τ
=0 ;
∂y
∂τ
=1
∂t
∂ U
∂ U  −η  ∂ U
=
 +
∂t
∂η  2 t  ∂τ
∂ U
∂U
=
∂y
∂η
substituindo
1
4υt
− 2η
∂ ∂ U
∂ y  ∂ y
2
 = ∂ ∂U ∂ η ∂ η = ∂ U 1
 ∂η  ∂η ∂ y  ∂ y



∂ η 2 4υt
∂U
∂U
∂2 U
+ 4τ
=
∂η
∂τ
∂ η2
Condições de contorno
1) η=0; U =Uo
2) η→ ∞ e τ=0; U=0
5
∂U
∂2 U
∂U
4τ
2
=
+
η
∂τ
∂η
∂ η2
Utilizando separação de variáveis: U(η, τ) = H(η) T(τ)
− 2η T
d H
dη
+ 4τ H
dT
dτ
=T
d2 H
d η2
4τ d T
1 d 2 H 2η d H
2
λ
=
+
=
−
T dτ
H d η2
H dη
dT
T
λ2 dτ
=−
4 τ
ln T = −
λ2
4
ln τ + ln C
T =Cτ
−
λ2
4
Condições de contorno
1) τ=0 ; T =finito ⇒ λ=0 e T = constante
T=1 e
U(η) = H(η)
6
d2 U
Resultando em
d η2
+ 2η
dU
=0
dη
Condições de contorno e inicial
1) η = 0 ; U =1
2) η → ∞ ; U → 0
A condição de contorno (1) corresponde a condição de não deslizamento, enquanto
que a condição (2) engloba a condição inicial e no infinito, pois η = y/(4 υ t)0,5
Para integrar esta equação diferencial ordinária de 2a.
ordem, observa-se que esta equação é de 1a. ordem para
dφ
+ 2η φ = 0
dη
⇒
dφ
φ
= −2 η d η
2
2
dU
−
η
−
η
⇒
= C1 e
φ = C1 e
dη
⇒
η
φ=
dU
dη
ln φ = − η 2 + ln C1
2
η
−
'
U = C1 ∫ e
dη '
0
+ C2
7
η
U = C1 ∫ e
− η '2
dη ' + C 2
0
Condições de contorno e inicial
1) η = 0 ; U =1
C1 = −
2) η → ∞ ; U → 0
1
∞
∫ e
então
⇒ C2 = 1
− η '2
=−
dη '
2
π
0
2 η − η '2
U (η ) = 1 −
dη ' = 1 − erf (η ) = erfc(η )
∫ e
π 0
erf é a função erro e erfc é a função complementar


y
)
u ( y , t ) = u o 1 − erf (

4 υ t 


y
u ( y , t ) = u o erfc(
)

4 υ t 
A espessura de penetração pode ser definida como a distância da placa onde
a velocidade é 1% de uo. Neste caso, η ≈ 2, logo
δ =4 υt
8
Exemplo: Escoamento transiente entre duas placas
paralelas
Hipóteses:
1. Fluido Newtoniano
2. Propriedades constantes (ρ=cte, µ=cte)
3. 2-D (largura w >> b) ⇒ ∂ /∂ z = 0
4. L >> b ⇒ ∂ /∂ x = 0
5. Escoamento horizontal, gravidade
vertical
6. p=patm=cte
7. laminar
Como já vimos, a equação da continuidade incompressível é
o que implica que

∇ •V = 0


V = u( y, t ) i
9
Vimos que a equação de conservação de quantidade de movimento se
reduz a
Condição inicial
Condições de contorno, t >0
∂ u
∂ 2u
=υ
1) t ≤ 0 ; u =0
1) y=0; u =vo
2
∂t
∂y
Adimensionalizando
para 0 < y ≤ b
u
U=
vo
1 ∂ U υ ∂ 2U
=
∆tref ∂ τ b 2 ∂ η 2
2) y=b, u=0
y
η=
b
⇒ ∆t ref
τ=
t
∆t ref
b2 τ = t υ
=
υ
b2
O tempo característico corresponde aproximadamente ao
tempo para o momentum se difundir em uma distância b
∂U ∂ U
=
∂τ
∂η 2
2
Condições de contorno e inicial
1) τ ≤ 0 ; U =0 2)η=0; U=1
3) η=1; U=0
10
Procura-se solução do tipo:
U = U ∞ (η ) − U t (η , τ )
U∞ é a solução em regime permanente e Ut é a parte transiente da solução que
desaparece quando t →∞
Substituindo na equação diferencial obtém-se
d 2U ∞
dη
2
∂ U t ∂ 2U t
=
∂τ
∂η 2
=0
Condições de contorno,
Condições de contorno e inicial
1) η=0; U∞ =1
1) τ=0; Ut =U∞
2) η=1, U ∞ =0
2) η=0, U t =0
3) η=1, U t =0
Primeiro vamos encontrar a solução em regime permanente
d 2U ∞
dη 2
= 0 ⇒ U ∞ = C1 η + C 2
U ∞ (η ) = 1 − η
Condições de contorno
1) η=0; U∞=1 ⇒ C2=1
2) η=1; U ∞ =0 ⇒ C1=-1
11
Para resolver
∂ U t ∂ 2U t
=
∂τ
∂η 2
Vamos assumir uma solução do tipo
U t = f (η ) g (τ )
Separação de
variáveis
Substituindo na equação diferencial e dividindo por f g obtém-se
1 d g 1 d2 f
=
d
τ
g
f dη 2
Como τ e η são variáveis independentes, e como o lado direito só depende de η
e o esquerdo de τ, então ambos os lados devem ser iguais a mesma constante.
Vamos definir esta constante como – c2, o que nos permite escrever
d g
= − c2 g
dτ
d2 f
dη
2
+ c2 f = 0
⇒
⇒
2τ
−
c
g = Ae
Problema de
Sturm-Liouville
f = B sin (c η ) + C cos (c η )
12
Ut = A e
−c 2 τ
[B sin( cη )+C cos(cη )]
Condições de contorno
1) η=0, U t =0 ⇒ C = 0
2) η=1, U t =0 ⇒ sin (c) = 0 , pois B =0 implica em solução trivial Ut=0
Porém existem infinitos valores c que satisfazem esta condição, i.e.,
são os auto-valores
cn=n π,
n= 0, ±1, ±2, ± 3, .....
Para cada auto-valores, existe uma auto-função correspondente fn e
função gn
f n = B n sin ( n π η )
n= 0, ±1, ±2, ± 3, .....
g n = An e
−n2 π 2 τ
13
Cada produto gn fn satisfaz a equação diferencial, então a solução
completa é a soma do todas as soluções particulares
Ut =
+∞
∑ Dn exp(− n 2 π 2 τ ) sin( n π η )
n = −∞
onde Dn = An Bn.
Como o termo n=0 é nulo e sin (-n πη )= - sin (n π η ), podemos omitir o
valor nulo e negativos de n.
+∞
U t = ∑ Dn exp(− n 2 π 2 τ ) sin( n π η )
n =1
Aplicando a condição inicial: τ=0, U t = U∞ temos
+∞
1 − η = ∑ Dn sin( n π η )
n =1
Para determinar as constantes Dn precisamos explorar a condição de
ortogonalidade.
14
ORTOGONALIDADE DE AUTO-FUNÇÕES
Considere a equação:
[
d2 y
]
dy
+ f1 ( x )
+ f 2 ( x ) + λ2 f 3 ( x ) y = 0
dx
d x2
Esta equação é típica em problemas uni-dimenisonais de transferência de calor e
mecânica dos fluidos.
Considere a equação submetida a condições de contorno homogêneas no
intervalo (a, b).
A solução deste problema irá gerar autofunções ϕn (x) correspondentes a
autovalores λn (x).
A equação do exemplo transiente nas placas é um caso particular desta
equação, com y = f, f1=f2=0 e f3=1. λ=c é o auto-valor
2
d f
dη 2
+ c2 f = 0
15
A equação anterior pode ser reescrita como:
dy 
d 
p (x )
+


dx 
dx 
[q (x) + λ2 ω (x)] y = 0

∫ f ( x ) dx
 p (x ) = e 1

com q (x ) = p (x ) f 2 (x )

ω (x ) = p (x ) f 3 = f 3 (x ) e ∫ f1 (x ) dx

No exemplo do escoamento transiente entre placas:
p(x) =1 ; q(x)=0
; ω (x) =1
16
Funções ortogonais: Sejam ϕn (x) e ϕm (x) duas auto-funções
correspondentes a auto-valores λn e λm distintos. Estas funções
são ortogonais num intervalo (a, b) com respeito a função peso
ω(x) pois:
b
∫ ω ( x ) ϕ n ( x ) ϕ m ( x ) dx = 0 ; ( m ≠ n )
a
Voltando ao exemplo: Para determinar as constantes Dn vamos
utilizar a condição de ortogonalidade.
+∞
1
∫ (1−η ) sin( m π η ) d η = ∑ Dn
0

 n =1
1 /( mπ )
1
∫ sin( n π η ) sin( m π η ) d η
0


quando m ≠ n
=0
=1/2 quando m = n
então
2
Dn =
nπ
n = 1, 2, 3,...
17
A solução final é
+∞  2 
 exp(− n 2 π 2 τ ) sin( n π η )
U (η , τ ) = (1 − η ) − ∑ 
n =1  n π 
Observações:
 Exceto para os primeiros instantes de tempo, a série infinita converge
rapidamente, isto é, somente os primeiros termos contribuem de forma
apreciável.
No limite dos instantes de tempo inicias, essa solução é equivalente a
solução de uma única parede colocada em movimento abruptamente.
Pois para os primeiros instantes de tempo, o movimento do fluido só
ocorre próximo a placa inferior, como se o fluido “não sentisse” a
presença da parede em y=b.
18
Exemplo: Escoamento próximo ao uma placa
oscilante com descolamento X(t)= Xo sin ωt
Hipóteses:
1. Fluido Newtoniano
2. Propriedades constantes
(ρ=cte, µ=cte)
3. 2-D (largura b >> δ) ⇒
∂ /∂ z = 0
4. L >> δ ⇒ ∂ /∂ x = 0
5. Escoamento horizontal,
gravidade vertical
u (0, t ) = dX = X o ω cos(ω t )
d t 
6. p=patm=cte
7. laminar
vo
Como já vimos


V = u( y, t ) i
∂ u
∂ 2u
=υ
∂t
∂ y2
19
Condições de contorno, t >0
1) y=0 ; u =vo cos (ω t)
2) y→ ∞, u→ 0
Deseja-se a solução periódica permanente, isto é, após o
desaparecimento do transiente inicial logo, a condição inicial não é
necessária.
As partículas de fluido estarão sujeitas a oscilações com freqüência ω,
porém com ângulo de fase e amplitude que são função somente da
posição.
Para a obtenção desta solução “permanente periódica” é
conveniente utilizar uma técnica baseada em números complexos. A
solução desejada é a solução assintótica para t → ∞.
20
Números Complexos: definições básicas
Um número é complexo quando possui uma parte imaginária, i.e., uma
parte proporcional a
i = − 1 . Este número pode ser representado
no plano como mostrado na figura.
Observações:
 Representação cartesiana: a + b i
Representação polar: r (cos θ + i sin θ) = r eiθ
ℜ (a + b i ) = a é a parte real de a + b i
ℑ{a + b i} = b é a parte imaginária
21
(a + b i )2 = a 2 - b2 + 2 a b i
(a + b i ) (a - b i ) = a 2 + b2
(a + b i )-1 = (a - b i ) /[(a + b i ) (a - b i ) ]= (a - b i ) / (a 2 + b2)
Para encontrar (-i)0,5 na forma a+bi, proceder como segue
i = a + bi ⇒ i = ( a + b i ) 2 = a 2 − b 2 + 2 a b i
⇒ a 2 − b 2 = 0 e 2 a b= 1
i =±
então
1
i
=
1
2
i
( i)
2
(1 + i )
=− i =
1
(1 + i )
2
22
Voltando ao Escoamento próximo ao
Condições de contorno, t >0
uma placa oscilante com descolamento 1) y=0 ; u =v cos (ω t)= v ℜ{ eiω t}
o
o
X(t)= Xo sin ωt
2) y→ ∞, u→ 0
Procura-se solução do tipo:
u ( y , t ) = ℜ{v o ( y ) eiωt }
vo
é uma função complexa de y , tal que u (x,t) não estará necessariamente
em fase com u (0,t).
Substituindo na equação diferencial, obtém-se
2 o
d
v
o
i
t
ω
} = υ ℜ{
e iω t }
ℜ{v ( y ) i ω e
d y2
então
iω  o
−
v = 0
d y2  υ 
d 2v o
Condições de contorno, t >0
1) y=0 ; vo =vo
2) y→ ∞, vo → 0
23
A solução é
v o = C1 e
ou
v o = C1 e
y iω / υ
+ C2 e
y (1+i ) ω / 2υ
onde usou-se o fato de que
i =±
1
− y iω / υ
+ C2 e
− y (1+i ) ω / 2υ
(1 + i )
2
Condições de contorno, t >0
1) y=0 ; vo =vo ⇒ C2 = vo
2) y→ ∞, vo → 0
⇒ C1 = 0
vo = vo e
− y (1+i ) ω / 2υ
e
u ( x, t ) = ℜ{ v o e
− y (1+i ) ω / 2υ
e iωt } = v o e
− y ω / 2υ
ℜ{e
−i( y ω / 2υ −ω t
24
}
Finalmente a solução é
u( x, t ) = v o e
− y ω / 2υ
cos(ω t − y ω / 2υ )
Observações:
 O perfil de velocidade possui a forma de uma oscilação harmônica
amortecida, cuja amplitude é v o e
− y ω / 2υ
a uma distância y possui um atraso
, na qual uma camada de fluido
y ω / 2υ com respeito ao movimento
da parede.
 A influência do movimento da placa no fluido encontra-se restrita a
y < 5 ω / 2υ
Duas camadas de fluidos, separadas uma distância igual a 2 π /
ω / 2υ ,
oscilam em fase.
25
Exemplo: Inicialização de Escoamento




=
+
+
V
u
e
v
e
v
e
em Duto Circular
θ θ
x
r
gr
r
r
D=2 R
θ
gθ

g
x
g r = − g senθ
;
gθ = − g cos θ
Hipóteses:
1. Fluido Newtoniano
5. Escoamento horizontal, gravidade
vertical
2. Propriedades constantes
(ρ=cte, µ=cte)
6. Laminar
3. 2-D (axi-simétrico) ⇒ ∂ /∂ θ = 0
7. Fluido em repouso
4. L >> R ⇒ ∂ /∂ x = 0
8. t ≥ 0, gradiente de pressão imposto
Como já vimos, a equação da continuidade incompressível é
o que implica que


V = u(r , t ) i

∇ •V = 0
26
Q. M. L - direção x




∂ u

1 ∂  ∂u 
∂p
∂u
∂u
∂u
∂ 2u

=−
 r
 +
ρ + v
+µ
+
+ vθ
+ u
2
2

t
r
r
x
∂
∂
∂
θ
∂
∂x
r ∂ r  ∂ r  r ∂θ

 





zero ( v = 0) zero ( 4) zero (5)
zero ( 4)



2
∂ u 
∂
x2 

zero (5)
 1 ∂  ∂ u 
∂p
∂u
 r

=−
+ µ
ρ
∂t
∂x
 r ∂ r  ∂ r 
Condições de contorno : 1) η=0
Condição inicial:
1) τ=0
Adimensionalizando
U=
U=finito
U=0
uµ
− ∂ p / ∂ x R2
2) η=1
r
η=
R
1 ∂  ∂U
∂U
η
=1 +
∂τ
η ∂η  ∂η



U=0
τ=
tυ
R2
27
U = U ∞ (η ) + U t (τ , η )
∂ Ut 1 ∂  ∂ Ut
η
=
∂τ η ∂η  ∂η
1 ∂  ∂U∞ 
η
 + 1 = 0
η ∂η  ∂η 
Condições de contorno : 1) η=0
1) η =0
3) τ =0
e inicial
2) η=1
U∞=finito
2) η=1
Ut=finito
Ut = - U∞



U ∞ =0
U t =0
Condições de contorno :
1 ∂  ∂U∞ 
η
 + 1 = 0
η ∂η  ∂η 
U∞ = −
η2
4
+ C1 lnη + C2
1) η=0
U∞=finito
2) η=1
U ∞ =0
⇒ C1=0
⇒ C2=1/4
1
U ∞ = (1 − η 2 )
4
28
∂ Ut 1 ∂  ∂ Ut
η
=
∂τ η ∂η  ∂η



U t (τ , η ) = T (τ ) Ξ (τ , η )
1 dT
1 1 d  dΞ 
η
 = −λ2
=
T dτ Ξ η dη  dη 
dT
= − λ2 T
dτ
⇒ T = Co exp(−λ2 τ )
1 d  dΞ 
η
 = −λ2 Ξ
η dη  dη 
Funções de Bessel
29
Funções de Bessel
d
dx
dy 

(
)
p
x
+


dx 

d  p dθ 
2 s
x
+γ x θ =0
dx 
dx 
[q (x) + λ2 ω (x)] y = 0
2

µ
=

s− p+2

Definindo 
ν = 1 − p

s− p +2
p−s≠2
1

1− p


µ
2
Ζν  γ µ x 
Solução Geral : θ = x
ν
γ


Fracioário
Real
Zero ou Inteiro
(ν = n )
Imaginário
(ν = n )
p−s=2
(soluções particulares)
Jν
Jn
Ζν
J −ν (ou Yν )
Jn
Ζν
Fracioário
Zero ou Inteiro
Obs. Se


⇒
Funções de Bessel
de 1a e 2a espécie
Funções de Bessel
Ιν
Ιn
Ι −ν (ou Κν )
In
Modificadas de
1a e 2a espécie
trate-se de equações equidimensional, cuja solução geral é do tipo
θ = xr
30
Jν (m x ) =
∞
∑
k =0
(− 1)k
(mx / 2)2k +ν
k ! Γ(k + ν + 1)
Funções de Bessel
Yν (mx ) =
cos(νπ ) Jν (mx ) − J −ν (mx )
sen(νπ )
onde função Gama:
 Γ(1) = 0! = Ι 


 Γ(1 / 2 ) = π 1 / 2 


Γ(n + 1) = n Γ(n ) = n!

π

(
)
(
)
Γ
ν
Γ
ν
1
−
=

sen(πν )

31
∞
Ι ν (mx )= ∑
Funções de Bessel
Modificada
k = 0 k ! Γ(k + ν + 1)
Κν (mx )=
Io(x)
1
0
(mx 2 )2k +ν
π Ι −ν (mx ) − Ι ν (mx )
2
sen(νπ )
I1(x)
I2(x)
K2(x)
K1(x)
Ko(x)
32
Derivadas das Funções de Bessel:
[
]
mxν Ζ
d ν

ν −1(mx )
x Ζν (mx ) = 
ν
dx

− mx Ζν −1(mx )
[
para Ζ = J , Y , I
para Ζ = Κ
]
− mx −ν Ζ
para Ζ = J , Y , K
d −ν

ν +1(mx )
x Ζν (mx ) = 
ν Ζ
dx

mx
para Ζ = Ι
ν +1(mx )

Caso
especial,
para
ν =0
− m Ζ 1 (mx )
d
[Ζ  (mx )]= 
d x
m Ζ 1 (mx )
para Ζ = J , Y , Κ
para Ζ = Ι
( )
m Ζ ν −1 (mx ) − ν Ζ ν (mx )
d
x
[Ζ ν (mx )]= 
d x
m Ζ ν −1 (mx ) − ν x Ζ ν (mx )
( )
( )
− m Ζ ν +1 (mx ) + ν Ζ ν (mx )
d
x
[Ζ ν (mx )]= 
d x
m Ζ ν +1 (mx ) + ν x Ζ ν (mx )
para Ζ = J , Y , Κ
para Ζ = Κ
para Ζ = J , Y , Κ
para Ζ = Ι
33
Voltando ao problema
d  dΞ  2
η
 + λ Ξ η = 0
dη  dη 
d  p dθ 
2 s
x
+γ x θ =0
dx 
dx 
p−s≠2
p = 1; s = 1; µ = 1; v = 0;
função peso w(η) = η
Ξ = C1 J o (λ η ) + C2 Yo (λ η )
Ξ n = An exp(−λ n2 τ ) J o (λn η )
2

µ
=

s− p+2

Definindo 
ν = 1 − p

s− p +2
γ=λ
real
Condições de contorno :
1) η=0
Ξ = finito
⇒ C2=0
2) η=1
Ξ=0
⇒
Jo(λn)=0
∞
U t = ∑ An exp(−λ n2 τ ) J o (λn η )
n =1
34
Condição inicial :
τ =0
Ut = - U∞
1 1
∞
1
2
− (1 − η ) = ∑ An J o (λn η )
4
n =1
An =
2
∫ − (1 − η ) η J o (λn η ) dη
0 4
1
2
∫ η J o (λn η ) dη
0
An = −
(
J 2 (λn ) /( 2λ2n )
0,5 [ J o (λn )]2 + [ J1(λn )]2
An = −
J1(λn ) / λ3n
0,5[ J1(λn )]2
)
mas
J 2 (λn )
2λ2n
=
J1(λn )
λ3n
−
J o (λn )
2λ2n
J o (λn ) = 0
An = −
2
λ3n J1(λn )
∞
1
2
2
U = (1 − η ) − ∑
exp(−λ n2 τ ) J o (λn η )
3
4
n =1 λn J1(λn )
35
As primeras raizes da função de Bessel encontram-se na tabela
abaixo para valores positivo de n inteiro. Podem ser encontradas em
Mathematica usando o comando BesselJZero[n, k].
J 2 (λ n )
J 3 (λ n )
J 4 (λ n )
J 5 (λ n )
3.8317
5.1356
6.3802
7.5883
8.7715
7.0156
8.4172
9.7610 11.0647 12.3386
n
J o (λ n )
J 1 (λ n )
1
2.4048
2
5.5201
3
8.6537 10.1735 11.6198 13.0152 14.3725 15.7002
4 11.7915 13.3237 14.7960 16.2235 17.6160 18.9801
5 14.9309 16.4706 17.9598 19.4094 20.8269 22.2178
36
∞
1
2
2
U = (1 − η ) − ∑
exp(−λ n2 τ ) J o (λn η )
3
4
n =1 λn J1(λn )
Grafico de V x t
1
tau=0.0
tau=0.1
tau=0.2
tau=0.3
tau=0.4
reg perm
0.9
0.8
0.7
eta=r/R
0.6
0.5
0.4
0.3
0.2
0.1
0
-0.05
0
0.05
0.15
0.1
Velocidade U_{adim)
0.2
0.25
0.3
37
clc;
clear;
nn=1;
lambda_old(nn)=1;
for nn=1:1:12;
dif=1;
for iter=1:1:100
lambda(nn)=lambda_old(nn)+besselj(0,lambda_old(nn))/besselj(1,lambda_old(nn));
dif=abs(lambda(nn)-lambda_old(nn));
lambda_old(nn)=lambda(nn);
end
lambda_old(nn+1)=lambda_old(nn)+2.5;
end
lambda
38
for i=1:1:5
tau(i)=0.1*(i-1);
for j=1:1:11
eta(j)=0.1*(j-1);
vel_infty(j)=0.25*(1-eta(j)*eta(j));
velocidade_t(j)=0;
for n=1:1:12
dn=-2/(lambda(n)^3*besselj(1,lambda(n)));
velocidade_t(j)=velocidade_t(j)+
dn*exp(-lambda(n)^2*tau(i))*besselj(0,lambda(n)*eta(j));
end
vel(I,j)=vel_infty(j)+velocidade_t(j);
end
for j=1:1:11
vel_1(j)=vel(1,j);
vel_2(j)=vel(2,j);
vel_3(j)=vel(3,j);
vel_4(j)=vel(4,j);
vel_5(j)=vel(5,j);
end
figure(1)
plot(vel_1 ,eta,vel_2,eta,vel_3,eta,vel_4,eta,vel_5,eta,vel_infty,eta);
legend('tau=0.0','tau=0.1','tau=0.2','tau=0.3','tau=0.4','reg perm') ;
title('Grafico de V x t');
ylabel('eta=r/R');
xlabel('Velocidade U_{adim)');
39