'
$
Fı́sica III - 4320301
Escola Politécnica - 2011
GABARITO DA PR
&
%
28 de julho de 2011
Questão 1 (a) (1,0 ponto) Use a lei de Gauss para calcular o vetor campo elétrico produzido por
um fio retilı́neo infinito com densidade linear de carga λ.
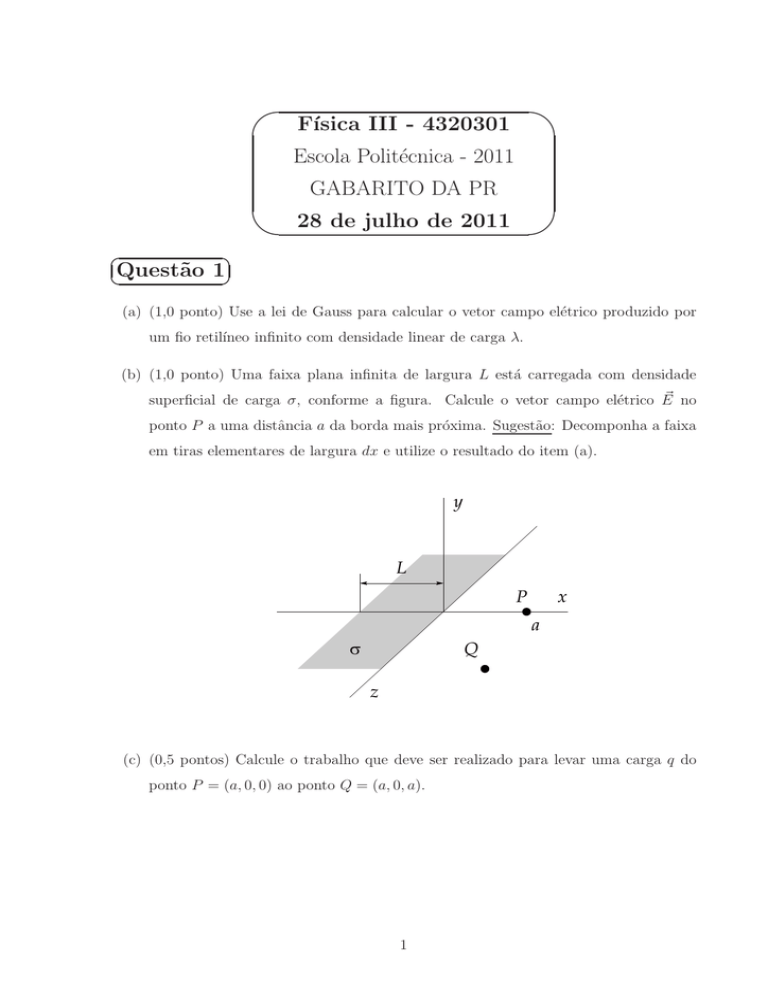
(b) (1,0 ponto) Uma faixa plana infinita de largura L está carregada com densidade
~ no
superficial de carga σ, conforme a figura. Calcule o vetor campo elétrico E
ponto P a uma distância a da borda mais próxima. Sugestão: Decomponha a faixa
em tiras elementares de largura dx e utilize o resultado do item (a).
y
L
P
x
a
σ
Q
z
(c) (0,5 pontos) Calcule o trabalho que deve ser realizado para levar uma carga q do
ponto P = (a, 0, 0) ao ponto Q = (a, 0, a).
1
Solução da questão 1
~ = E(r)b
(a) Devido à simetria cilı́ndrica E
r , onde r é a distância ao fio. Tomando-se
uma superfı́cie gaussiana cilı́ndrica, de altura h e raio r centrada no fio, obtemos
Z
λ
~ · dA
~ = 2πrhE(r) = Qint = λh .
E
Logo E(r) =
.
ǫ0
ǫ0
2πǫ0 r
S
(b) Uma tira de largura dx tem densidade linear de carga na direção z igual a σdx.
Usando o resultado do item (a), o campo elétrico produzido por uma tira entre x e
x + dx no ponto P é
~ =
dE
σdx
~ı.
2πǫ0 (a − x)
y
x+dx
x
P
−L
x
a
Q
σ
z
O campo total é
~ = σ~ı
E
2πǫ0
Z
0
−L
σ
dx
ln
=
a−x
2πǫ0
a+L
~ı.
a
~ é perpendicular a d~l ao longo do segmento de reta P Q. Logo
(c) E
Z Q
~ · d~l = 0.
W = −q
E
P
2
Questão 2 Considere duas cascas esféricas condutoras concêntricas sendo que a casca interior possui
raio a e a exterior raio b. O espaço entre as cascas é preenchido uniformemente com um
material cuja resistividade é ρ. Entre os duas cascas é aplicada uma diferença de potencial
tal que a corrente da casca interna para a externa é I0 . As respostas dos itens abaixo
deverão ser dadas em função apenas dos dados do problema que são a, b, I0 e ρ.
b
a
I0
ρ
(a) (1,0 ponto) Calcule o vetor densidade de corrente a uma distância r (a < r < b) do
centro das esferas.
(b) (0,5 ponto) Determine o vetor campo elétrico entre as cascas esféricas.
(c) (0,5 ponto) Usando o campo elétrico obtido em (b), calcule a diferença de potencial
V da esfera interna relativamente à esfera externa (V = Va − Vb ).
(d) (0,5 ponto) Calcule a resistência do sistema.
3
Solução da questão 2
(a) Densidade de corrente
A relação entre a corrente e a densidade
de corrente é dada por
Z
~ = J(r)4πr 2
I=
J~ · dA
S
r
S
Logo,
~ = I0 b
J(r)
er
4πr 2
(b) O campo elétrico é calculado com a lei de Ohm
1~
ρI0
~
J~ = E
=⇒ E(r)
ebr
=
ρ
4πr 2
(c) A diferença de potencial entre as cascas é
V = Va − Vb = −
Za
~ · d~ℓ = − ρI0
E
4π
Za
1
ρI0
dr =
2
r
4π
b
b
(d) A resistência é
V
ρ
R=
=
I0
4π
4
1 1
−
a b
1 1
−
a b
.
Questão 3 A figura abaixo mostra a seção reta de um condutor cilı́ndrico infinito, oco, com raio
interno a e raio externo b. Pelo condutor passa uma corrente I uniformemente distribuı́da
na seção reta e dirigida para fora da página.
1111111111111111111
0000000000000000000
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
0000000000000000000
1111111111111111111
a
r
b
Usando a lei de Ampère, calcule:
(a) (0,5 ponto) o vetor campo magnético na cavidade do condutor (0 < r < a);
(b) (1,0 ponto) o vetor campo magnético no interior do condutor (a < r < b);
(c) (0,5 ponto) o vetor campo magnético no exterior do condutor (r > b).
(d) (0,5 ponto) Esboce as linhas de campo magnético nas três regiões.
5
Solução da questão 3
A lei de Ampère afirma que
I
~ · d~ℓ = µ0 Itotal ,
B
C
onde Itotal é a corrente que atravessa uma superfı́cie aberta limitada pela curva C.
~ tem simetria cilı́ndrica: B
~ = B(r) ϕ.
Neste problema o campo B
b Assim, é conveniente
escolher para C um cı́rculo com centro no eixo do cilindro e contido num plano perpen-
~ k d~ℓ e
dicular a este eixo, como é sugerido na figura. Neste caso, B
I
I
~
~
Bdℓ = 2πrB(r) .
B · dℓ =
C
C
Substituindo na lei de Ampére obtemos
B(r) =
µ0
Itotal .
2πr
(a) Na cavidade do condutor (0 < r < a) Itotal = 0 e
~ = ~0 .
B(r) = 0 =⇒ B
(b) No interior do condutor (a < r < b) a densidade de corrente é
J=
I (r 2 − a2 )
I
2
2
=⇒
I
=
π(r
−
a
)J
=
.
total
π(b2 − a2 )
b2 − a2
O campo magnético é
µ0 I
B(r) =
2π(b2 − a2 )
r 2 − a2
r
µ0 I
~ =
=⇒ B
2π(b2 − a2 )
r 2 − a2
r
ϕ
b .
(c) No exterior do condutor (r > b) Itotal = I e
B(r) =
(d) Linhas de campo.
µ0 I
~ = µ0 I ϕ
=⇒ B
b .
2πr
2πr
As linhas de campo são cı́rculos
b
concêntricos conforme a figura ao lado.
a
As flechas indicam o sentido do campo
~ que é tangente às linhas de campo.
B
B
6
Questão 4 No circuito da figura a chave 2 está aberta e a chave 1 está fechada há muito tempo,
encontrando-se o circuito numa situação estacionária.
1
ε
R1
2
L
R2
(a) (0,5 ponto) Determine a corrente I0 através do indutor.
(b) (1,0 ponto) No instante t = 0 a chave 2 é fechada e simultaneamente a chave 1 é
aberta. Escreva a equação diferencial e obtenha a corrente I(t) através do indutor
para t ≥ 0.
(c) (1,0 ponto) Mostre que a energia total dissipada no resistor R2 para t ≥ 0 é igual à
energia que estava armazenada no indutor.
7
Solução da questão 4
(a) No regime estacionário o indutor se comporta como um condutor com resistência
nula. Portanto,
I0 =
ε
.
R1
(b) Após abrirmos a chave 1 e fecharmos a chave 2, obtemos um circuito RL cuja
equação diferencial é
dI
L + R2 I = 0 =⇒
dt
ZI
Zt
R2
dI
=−
I
L
I0
dt =⇒ ln
I0
I
=−
R2
t ⇔ I = I0 e−R2 t/L .
L
0
(c) A potência dissipada é dada por
Ediss =
Z∞
0
2
R2 I dt =
R2 I02
Z∞
−2R2 t/L
e
0
dt = −
R2 I02
∞
1
L −2R2 t/L = LI02
e
2R2
2
0
que é igual à energia armazenada inicialmente no indutor.
8
Formulário
qq ′(~r − ~r′ )
F~ =
,
4πǫ0 |~r − ~r′ |3
Z
dq
q(~r − ~r′)
1
~
,
E=
r̂,
′
3
4πǫ0 |~r − ~r |
4πǫ0
r2
Z
I
~
~
~
~ · dA
~ = qint ,
U = −~p · E, ΦE = E · dA,
E
ǫ0
~
F~ = q E,
~ =
E
q
,
V =
4πǫ0 |~r − ~r′ |
VB − VA = −
ZB
1 X qi
V =
,
4πǫ0 i ri
1 X qi qj
U=
,
4πǫ0 i<j rij
p = qd,
~
~τ = ~p × E,
1
V =
4πǫ0
~ · d~ℓ,
E
A
1
1
1
=
+
+ ... ,
Ceq
C1 C2
σ
E= ,
ǫ
ǫ
u = E2,
2
U=
I
C = Q/V,
Q2
CV 2
QV
=
=
,
2C
2
2
~ · dA
~ = qint−liv ,
ǫ0 κE
dq
,
r
~ = −∇V,
~
E
Ceq = C1 + C2 + ... ,
ǫ
= κ,
ǫ0
I=
Z
u=
ǫ0 2
E ,
2
dQ
= n|q|vd A,
dt
E=
E0
,
κ
J~ = n|q|~vd ,
dℓ
V2
dR = ρ , V = RI, V = E −Ir, P = V I = I 2 R =
,
A
R
Z
I
~
~
~ · dA
~ = 0, dF~ = Id~ℓ × B,
~
~
ΦB = B · dA,
B
µ
~ = I A,
ρ(T ) = ρ0 [1+α(T −T0 )],
~ + q~v × B,
~
F~ = q E
~
~τ = ~µ × B,
~
U = −~µ · B,
~
~ = µ0 I dℓ × r̂ ,
dB
4π r 2
F
µ 0 I1 I2
=
,
ℓ
2πr
~ 0 = µ0 H,
~
~ m = µ0 M
~, M
~ = χm H,
~
B
B
Z
I
d
~
~ · dA,
~ Φtotal = Nφespira = LI,
~
B
E · dℓ = −
dt
u=
B2
,
2µ0
U=
LI 2
,
2
u=
B2
,
2µ
9
E =−
I
~ · d~ℓ = µ0 Iint ,
B
dΦm
,
dt
Φtotal
= N2 φespira = M21 I1 ,
21
µ = κm µ0 = (1 + χm )µ0 .