Universidade Federal do Pará Centro de Ciências Exatas e Naturais

Universidade Federal do Pará
Centro de Ciências Exatas e Naturais
Departamento de Física
Laboratório Básico III
Experiência 03
CIRCUITO R.L.C. EM SÉRIE (RESSONÂNCIA).
1. OBJETIVO
Estudar o comportamento de um circuito RLC série em ressonância.
.
2. FUNDAMENTOS TEÓRICOS
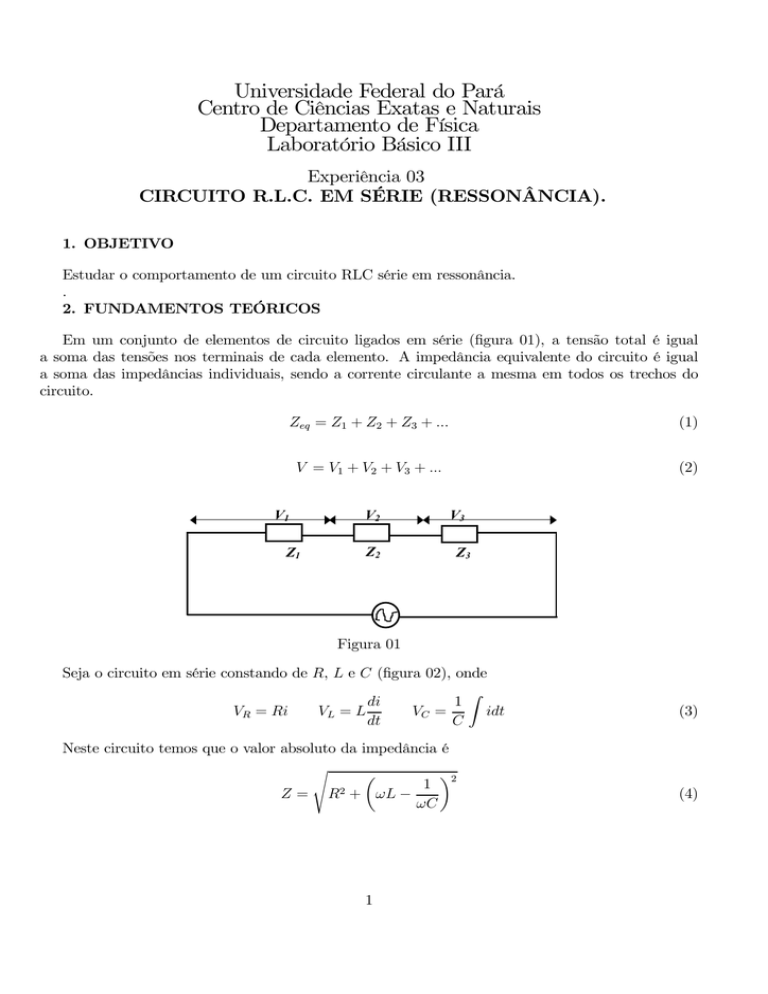
Em um conjunto de elementos de circuito ligados em série (figura 01), a tensão total é igual
a soma das tensões nos terminais de cada elemento. A impedância equivalente do circuito é igual
a soma das impedâncias individuais, sendo a corrente circulante a mesma em todos os trechos do
circuito.
Zeq = Z1 + Z2 + Z3 + ...
(1)
V = V1 + V2 + V3 + ...
(2)
V1
Z1
V2
Z2
V3
Z3
Figura 01
Seja o circuito em série constando de R, L e C (figura 02), onde
Z
di
1
VC =
idt
VL = L
VR = Ri
dt
C
Neste circuito temos que o valor absoluto da impedância é
s
¶2
µ
1
Z = R2 + ωL −
ωC
1
(3)
(4)
1 /ω C
ωL
R
VR
VC
VL
i
Figura 02
Para este circuito o ângulo de fase é dado por
µ
ωL −
φ = arctan
R
1
ωC
¶
.
(5)
Este circuito estará em ressonância quando a reatância do mesmo for nula, X = 0, isto é, quando
o circuito se tornar puramente resistivo. Nestas condições teremos que XL = XC , implicando que
1
ω = ω0 = √
LC
(6)
Assim teremos que para um circuito RLC em ressonância, sua freqüência será dada por
f0 =
1
√
2π LC
[Hz]
(7)
O amortecimento relativo de um oscilador é expresso por um número para o qual usa-se em geral a
letra Q como símbolo representativo. Q é denominado “F ator de Qualidade”, sendo definido como
Q = 2π
máxima energia armazanada
energia média dissipada por ciclo
(8)
Para o circuito RLC em série aqui considerado, o fator de qualidade é dado pela expressão
Q=
ωL
1
=
R
ωCR
(9)
O fator de qualidade de um circuito R.L.C. em série pode também ser expresso em função da
largura de faixa ou banda (B) e da freqüência de ressonância.
Q=
ω0
f0
f0
=
=
ω2 − ω1
f2 − f1
B
(10)
onde f1 e f2 são denominadas freqüências de corte, ou freqüências dos pontos de meia potência, e
imax
Vmax
correspondem aos pontos em que i = √ ou V = √ sendo a potência fornecida igual a metade
2
2
do valor máximo obtido em ressonância.
2
3. QUESTÕES
1. Na condição de ressonância, o que acontece com o valor da impedância e o valor da corrente?
Por que?
2. Qual o valor do ângulo de fase na condição de ressonância?
3. Em um circuito RLC em série ressonante, a energia armazenada é constante?
4. Demonstre as expressões do fator de qualidade. Dê o significado físico.
Q=
ωL
R
e
Q=
f0
B
5. Mostre que a freqüência de ressonância é a média geométrica das freqüências de corte ou
freqüências de meia potência.
p
f0 = f1 .f2
6. Nas freqüências de meia potência inferior e superior, o que ocorre com as reatâncias indutivas
e capacitivas?
7. Demonstre que
Z=
s
¶2
µ
1
R2 + ωL −
ωC
e
µ
ωL −
φ = arctan
R
8. Na condição de ressonância, tensão e corrente estão em fase. Por que?
4. MATERIAL UTILIZADO
-
Resistência
Indutor
Capacitor
Gerador de audio
Cabos de conexão
Papel milimetrado (traga de casa)
5. PROCEDIMENTO EXPERIMENTAL
1. Monte o circuito da figura abaixo
R
L
VR
VL
A
4Ω
3
C
VC
1
ωC
¶
2. Certifique-se de que a montagem está correta, chame o professor ou monitor.
3. Faça uma previsão teórica da freqüência de ressonância. Verifique se é compatível com as
freqüências fornecidas pelo gerador.
4. Verifique a escala da fonte de freqüência.
5. Obtenha a curva de ressonância qualitativamente, variando a freqüência em um intervalo
largo ao redor do valor por você previsto e observe as indicações nos multitestes (voltímetros e
amperímetros). Agora que você já tem uma idéia geral de como se comportarão os elementos, vamos
efetuar as medidas de fato. Observe no amperímetro quando a corrente inverte o sentido e nos
voltímetros, quando VL = VC .
6. Varie a freqüência (escolha intervalos adequados) e anote em uma tabela os respectivos valores
de I, VR , VL , VC e V .
f
I
VR
VL
VC
V
Obs.
7. Troque o valor da resistência e faça novas medidas.
6. TRATAMENTO DE DADOS
1. Construa as curvas I x f, VR x f, VL x f e VC x f . Observação: construa o gráfico para as
diferentes resistências no mesmo eixo para você poder comparar melhor.
2. Construa os gráficos Z x f , XC x f , XL x f e R x f , todos em um mesmo gráfico.
3. Determine a freqüência de ressonância. Compare o valor teórico e o valor experimental.
4. Determine o fator de qualidade experimentalmente na freqüência de ressonância e compare
com o valor teórico determinado para a mesma freqüência. Qual a influência do valor de R?
5. Qual o valor da largura de banda de sua experiência? Determine-o.
6. Determine as reatâncias indutivas e capacitivas para as freqüências dos pontos de meia potência.
7. Faça um comentário geral após comparar os diferentes gráficos obtidos para diferentes resistências.
4
7. BIBLIOGRAFIA
1. RESNICK, R. , HALIDAY, D. , Fundamentos da Física, Volume IV, 6a Edição, Livros Técnicos
Científicos, 1996
2. SERWAY, R. A., Física, Volumes IV, , 3a Edição, Livros Técnicos e Científicos, 1992.
3. RAMOS, Luis Antônio Macedo, Física Experimental, Porto Alegre, Mercado Aberto, 1984.
4. DANO, Higino S., Física Experimental I e II, Caxias do Sul, Editora da Universidade de
Caxias do Sul, 1985.
5. SILVA, Wilton Pereira, CLEIDE M. D. , Tratamento de Dados Experimentais, 2a Edição, João
Pessoa, Editora Universitária, 1998.
6. VUOLO, Jose Henrique, Fundamentos da Teoria de Erros, 2a Edição, Editora Edgar BLUCHER
7. GOLDEMBERG, JOSÉ, Física Geral e Experimental, Volume II.
5