Questõesdecinemática4

 Prof. A.F.Guimarães Questões Cinemática 4 – Gráficos Questão 1 s(m)
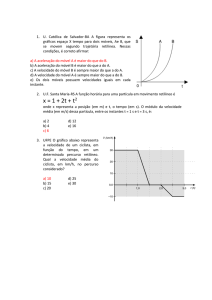
instante 3s, depois mais 2m do instante 4s até o instante 6s e finalmente 3m do instante 8s até o (UEL) O gráfico a seguir representa o movimento instante 10s. O item está certo. de uma partícula. Letra “E”. Questão 2 7
6
5
4
3
2
1
0
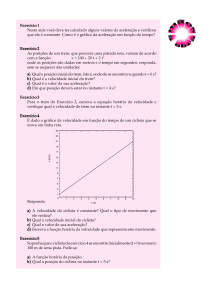
(UFES) Uma partícula move‐se numa trajetória retilínea com a velocidade mostrada no gráfico a seguir. 12
0
1
2
3
4
5
6
7
8
10
9 10 11 12
v(m/s)
t(s)
Analise as afirmativas seguintes: I. A velocidade escalar média entre t = 4s e t = 6s é de ‐1m s ‐1. II. O módulo do deslocamento entre t = 4s e t = 10s é de 1m. III. A distância total percorrida desde t = 0 até t = 10s vale 8m. A( ). Somente I é correta. B( ). Somente I e II são corretas. C( ). Somente I e III são corretas. D( ). Somente II e III são corretas. E( ). I, II e III são corretas. 8
6
4
2
0
0
2
3
4
5
6
7
8
9
10
t(s)
Determine: a) o deslocamento da partícula no intervalo 0s a 9s; b) a velocidade média no intervalo 0s a 9s; c) a aceleração no instante 5s. Resolução: a) Podemos determinar o espaço percorrido por meio do cálculo da área da figura formada no gráfico (V x t). Assim, teremos: B ⋅ h 9 ⋅10
A∆ =
=
= 45
2
2
∴ ∆S = 45m.
b) Utilizando a definição de velocidade escalar média, teremos: ∆S 45
vm =
=
= 5m ⋅ s−1. ∆t
9
c) A aceleração pode ser obtida a partir da inclinação da reta entre os instantes 4s e 9s. Resolução: I. No trecho entre os instantes t = 4s e t = 6s, a inclinação da reta fornecerá a velocidade escalar média. Assim, ∆S 3 − 5
vm =
=
= −1m ⋅ s−1. ∆t
2
O movimento entre esses instantes é retrógrado. Certo o item. II. A variação do espaço vale: ∆S = S − S0 = 6 − 5 = 1m . O item está certo. III. A distância total percorrida é dada por: d = 3 + 2 + 3 = 8m . Do gráfico, podemos observar que o móvel percorreu 3m do instante 0 até o 1 www.profafguimaraes.net 1
Ou da definição de aceleração escalar média. Letra “B”. Assim, teremos: Questão 4 ∆v 0 −10
am =
=
= − 2 m ⋅ s −2 . ∆t
5
(UFPR) O gráfico a seguir representa a velocidade em função do tempo para uma partícula em Neste trecho o movimento é progressivo e movimento retilíneo. Com base nesse gráfico, é retardado. correto afirmar que: Questão 3 40
(FUVEST) Um automóvel faz uma viagem em 6 horas e sua velocidade escalar varia em função do tempo aproximadamente como mostra o gráfico. A velocidade escalar média do automóvel na viagem é: v(km h‐1) 60 30 0 1 2 3 4 5 6 t h) A( ). 35 km h ‐1; B( ). 40 km h ‐1; C( ). 45 km h ‐1; D( ). 48 km h ‐1; E( ). 50 km h ‐1; 30
v(m/s)
20
10
0
‐10 0
4
6
8
10
12
14
16
18
20
‐30
t(s)
(01)No instante t = 6s a velocidade é nula. (02)No intervalo entre t = 2s e t = 4s a velocidade é negativa. (04)No intervalo entre t = 0 e t = 6s a aceleração vale ‐5m s ‐2. (08)Entre t = 12s e t = 14s a aceleração é positiva. (16)O deslocamento da partícula no intervalo entre t = 0 e t = 6s vale 45 m. (32)O valor de velocidade no instante t = 4s não volta a se repetir em nenhum instante posterior. Soma: Resolução: 01‐ Observando o gráfico, podemos concluir que a velocidade é nula no instante t = 6s. Certo. 02‐ A partir do gráfico, podemos observar que a velocidade é positiva nesse intervalo de tempo. Errado. 04‐ A partir da inclinação da reta, podemos determinar a aceleração do móvel. ∆v 0 − 30
am =
=
= −5m ⋅ s−2 . ∆t
6
Certo. 08‐ Observando o gráfico, a partir do instante t = 10s, a inclinação da reta mostra que a velocidade é crescente, portanto a aceleração é positiva. Certo. Resolução: Previamente, determinaremos o espaço percorrido pelo móvel durante as 6 horas de movimento. Por meio do cálculo das áreas formadas no gráfico (V x t), teremos o referido espaço. Assim, At = 30 ⋅ 2 + 60 ⋅ 3 = 240
∴ ∆S = 240km.
Utilizando a definição de velocidade escalar média, teremos: ∆S 240
vm =
=
= 40km ⋅ h−1. ∆t
6
2 www.profafguimaraes.net 2
‐20
16‐ A partir da área da figura formada no gráfico (V x t) entre os referidos instantes podemos determinar o espaço percorrido. Assim, teremos: B ⋅ h 30 ⋅ 6
A∆ =
=
= 90
2
2
∴ ∆S = 90m.
Errado. 32‐ O valor da velocidade para o instante t = 4s volta a se repetir após o instante t = 14s. Errado. Soma: 13. t = 6s e t = 2s poderemos determinar os referidos valores. Assim, para t = 6s, temos: 0 = 6v0 −18 g p ⇒ v0 = 3 g p . (5.1) Para t = 2s, temos: 8 = 0 + 2v0 − 2 g p ⇒ v0 − g p = 4. (5.2) Utilizando o resultado (5.1) em (5.2) temos: 3 g p − g p = 4 ⇒ g p = 2 m ⋅ s −2 . Utilizando o resultado (5.1), temos: v0 = 3 g p = 6m ⋅ s−1. Questão 5 (FUVEST) A figura representa o gráfico posição‐
tempo do movimento de um corpo lançado verticalmente para cima com velocidade inicial v0, na superfície de um planeta. Qual o valor: a) 2m s ‐2. b) 6m s ‐1. Questão 6 (UNICAMP) O gráfico a seguir representa aproximadamente a velocidade de um atleta em função do tempo em uma competição olímpica. 10
posição(m)
8
6
4
Velocidade (m/s)
2
0
0
1
2
3
4
5
6
7
tempo(s)
a) da aceleração da gravidade na superfície do planeta? b) da velocidade inicial v0? 14
12
10
8
6
4
2
0
0
4
6
8
10 12 14 16 18 20
tempo(s)
Resolução: Considerando que o gráfico de (S x t) é uma parábola, podemos então utilizar a equação horária do espaço para determinar a aceleração e a velocidade inicial. Assim, temos: g t2
h = h0 + v0t − p . 2
A posição inicial do móvel, observando o gráfico é dada por h0 = 0. Utilizando os dados dos instantes a) Em que intervalo de tempo o módulo da aceleração tem o menor valor? b) Em que intervalo de tempo o módulo da aceleração é máximo? c) Qual é a distância percorrida pelo atleta durante os 20 s? d) Qual a velocidade média do atleta durante a competição? Resolução: 3 www.profafguimaraes.net 2
a) e b) Observando o gráfico podemos determinar a aceleração no intervalo de 0 a 6 s: ∆v 12
a0→6 =
= = 2 m ⋅ s −2 . ∆t
6
Já no intervalo de 16 a 20 s, a aceleração é negativa e vale: ∆v 10 −12
1
a16→20 =
=
= − m ⋅ s −2 . ∆t 20 −16
2
No intervalo de 6 a 16 s, a aceleração é nula. Assim, a aceleração possui o menor módulo no intervalo de 6 a 16s e possui maior módulo no intervalo de 0 a 6 s. c) O espaço percorrido pelo atleta será dado pela área no gráfico (V x t). Assim, tomaremos a área de dois trapézios, do intervalo de 0 a 16s e do intervalo de 16 a 20 s. Teremos: (16 +10)12
A1 =
= 156.
2
(12 +10) 4
A2 =
= 44.
2
∴ ∆S0→20 = 156 + 44 = 200m.
d) ∆S 200
vm =
=
= 10m ⋅ s−1. ∆t
20
A( ). A velocidade escalar inicial é nula e a aceleração é de ‐6 m s ‐2. B( ). A velocidade escalar inicial é 48 m s ‐1 e a aceleração escalar é de 6 m s ‐2. C( ). A aceleração escalar é de ‐39 m s ‐2. D( ). A velocidade escalar média no intervalo de zero a 2 s é de 9 m s ‐1. E( ). O espaço inicial é de 45 m, a velocidade escalar inicial é nula e a aceleração escalar é de +6 m s ‐2. Resolução: Se o vértice da parábola se encontra no eixo s, significa então que a velocidade escalar inicial é nula. Assim, tomando o valor do espaço igual a 48m com o seu respectivo instante t = 1 s, teremos: at 2
S = S0 + v0t +
2 (7.1) a
48 = S0 + .
2
Agora tomando o espaço igual a 57 m com seu respectivo instante t = 2 s, teremos: 57 = S0 + 2a . (7.2) Utilizando os resultados (7.1) e (7.2), teremos: a
57 − 48 = 2a − ⇒ 18 = 3a
2
−2
∴ a = 6m ⋅ s .
Logo o espaço inicial vale: Questão 7 57 = S0 + 12 ⇒ S0 = 45m. (ITA) A curva da figura é a representação gráfica da equação horária de um movimento retilíneo. Letra “E”. Ela é constituída por um trecho de um ramo de parábola cujo vértice está localizado no eixo s. Questão 8 Neste movimento: (UDESC) Dois ciclistas, A e B, partem da mesma s(m) posição no instante t = 0 e movimentam‐se no 57 mesmo sentido e em trajetória retilínea. Na figura 48 são mostrados os gráficos da velocidade em função do tempo dos dois ciclistas. t(s) 0 1 2 4 www.profafguimaraes.net II. O espaço percorrido pelo ciclista A, no intervalo de 0 a 15 s, é dado pela área do triângulo: 15 ⋅ 3
= 22,5 ∴ ∆S A = 22,5m. AA =
2
O espaço percorrido pelo ciclista B, para esse mesmo intervalo de tempo, é dado pela área do trapézio: (15 + 5)⋅ 3
= 30 ∴ ∆S B = 30m AB =
2
Como eles partiram simultaneamente da mesma posição, o ciclista B se encontra à frente do ciclista A. Logo o item está errado. III. O espaço percorrido pelo ciclista A, no intervalo de tempo de 0 a 20 s, é dado pela área do triângulo: 20 ⋅ 4
= 40 ⇒ ∆S A = 40m. AA =
2
O espaço percorrido pelo ciclista B, nesse mesmo intervalo de tempo, é dado pela área do trapézio: (20 + 10)⋅ 3
= 45 ⇒ ∆S B = 45m. AB =
2
O ciclista B ainda se encontra à frente do ciclista A. Item errado. IV. Utilizando os mesmos procedimentos acima, temos: 25 ⋅ 5
= 62,5 ⇒ ∆S A = 62,5m.
AA =
2
(25 +15)⋅ 3
AB =
= 60 ⇒ ∆S B = 60m.
2
O ciclista A percorreu 62,5 m enquanto o ciclista B percorreu 60 m. Como eles partiram simultaneamente do mesmo espaço, o ciclista A ultrapassou o ciclista B e se encontra a 2,5 m à frente. Item correto. Letra “B”. 6,0
v(m/s)
5,0
4,0
A
3,0
B
2,0
1,0
0,0
0,0
5,0
10,0
15,0
20,0
25,0
t(s)
Leia com atenção e analise as afirmações sobre os gráficos. I. A aceleração do ciclista B no intervalo de t = 0 a t = 10,0s foi maior do que a aceleração do ciclista A no intervalo de t = 0 a t = 25,0 s. II. No instante t = 15,0 s, o ciclista A ultrapassou o ciclista B. III. Decorridos 20,0 s, o ciclista A estava na frente do ciclista B. IV. Decorridos 25,0 s, o ciclista A estava na frente de B e a distância entre eles era igual a 2,5 m. Assinale a alternativa correta: A( ). Todas as afirmativas estão corretas; B( ). Somente estão corretas as afirmações I e IV; C( ). Somente estão corretas as afirmações I, III e IV; D( ). Somente estão corretas as afirmações II e III; E( ). Somente estão corretas as afirmações II, III e IV. Resolução: I. No intervalo de 0 a 10s, o ciclista B, desenvolveu uma aceleração dada por: ∆v
3
= = 0,3m ⋅ s−2 . aB =
∆t 10
O ciclista A, no intervalo de 0 a 25 s, desenvolveu uma aceleração dada por: ∆v
5
=
= 0, 2m ⋅ s−2 . aA =
∆t 25
Logo o item está correto. 5 www.profafguimaraes.net Questão 9 vm =
(UNICAMP) A figura a seguir mostra o esquema simplificado de um dispositivo colocado em uma rua para controle de velocidade de automóveis (dispositivo popularmente chamado de radar). Os sensores S1 e S2 e a câmera estão ligados a um computador. Os sensores enviam um sinal ao computador sempre que são pressionados pelas rodas de um veículo. Se a velocidade do veículo está acima da permitida, o computador envia um sinal para que a câmera fotografe sua placa traseira no momento em que esta estiver sobre a linha tracejada. Para um certo veículo, os sinais dos sensores foram os seguintes: d=2m
S2 S1 Câmera Computador Figura 1
S1 t(s) S2 0,1 0,2 0,3 t(s) Figura 2
a) Determine a velocidade do veículo em km h ‐1. b) Calcule a distância entre os eixos do veículo. Ou ainda, 20 ⋅ 3, 6 = 72km ⋅ h−1. b) No instante em que as rodas traseiras passam pelo sensor 1, as rodas dianteiras percorrem uma distância x para além do sensor 2. De acordo com o gráfico, esse instante vale 0,15s. Então, poderemos determinar x. O intervalo de tempo que as rodas dianteiras levam para percorrer x vale 0,15 – 0,1 = 0,05 s. Assim, x = vm ⋅∆t ⇒ x = 20 ⋅ 0, 05 = 1m. Logo, a distância entre os eixos vale: 2 + 1 = 3m. Questão 10 (DESAFIO) O espaço (e) de uma partícula variou com o tempo (t), conforme indica o diagrama a seguir: e(m) D e10
C 16 B 10 e0 A 0 1 2 3 4 5 6 7 8 9 10 t(s) No gráfico, os trechos AB, e CD são arcos de parábola, ao passo que o trecho BC é um segmento de reta. Determine: a) o espaço inicial (e0) da partícula; b) a aceleração escalar no trecho CD; c) o espaço (e10) da partícula em t = 10 s. Resolução: a) De acordo com o gráfico, o intervalo de tempo para que as rodas dianteiras percorram a distância que separam o dois sensores é de 0,1 s. Assim, podemos determinar a velocidade escalar média do automóvel utilizando a distância de 2 m entre os dois sensores. Logo, Resolução: Vamos, previamente, fazer algumas observações. Por se tratar de arco de parábola, vamos admitir então que o ponto A é o vértice do arco AB. Assim, podemos concluir que a velocidade da partícula no ponto A é nula. Para o 6 www.profafguimaraes.net ∆S
2
=
= 20m ⋅ s−1 . ∆t 0,1
arco CD vamos fazer a mesma colocação. Ou seja, o ponto D é o vértice do arco CD e a velocidade da partícula no ponto D também será nula. No segmento BC, a partícula executa um MU (movimento uniforme), pois, o gráfico é uma reta. Desta forma, a velocidade da partícula durante todo o intervalo de tempo de 5 até 7s é constante e vale: ∆S B→C 6
= = 3m ⋅ s−1. (10.1) vB →C =
∆t B→C
2
a) Para o arco AB podemos escrever a expressão para a velocidade escalar média dada por: ∆S A→ B v A + vB
vmA→B =
=
∆t A→ B
2
10 − e0 0 + 3
=
5
2
20 − 2e0 = 15
∴ e0 = 2,5m.
b) Para o arco CD podemos escrever a expressão da aceleração escalar instantânea dada por: ∆vC → D
a = constante = am =
∆tC → D
0−3
= −1m ⋅ s−2 .
a=
3
c) A equação horária para o trecho CD é dada por: 2
a (t D − tC )
e10 = eC + vC (t D − tC ) +
2
2
1⋅ 3
e10 = 16 + 3 ⋅ 3 −
2
∴ e10 = 20,5m.
7 www.profafguimaraes.net