LISTA ESPECIAL DE FÍSICA
1º ano
FÍSICA
Prof. Tourinho e
Prof Wesley
2º Bimestre
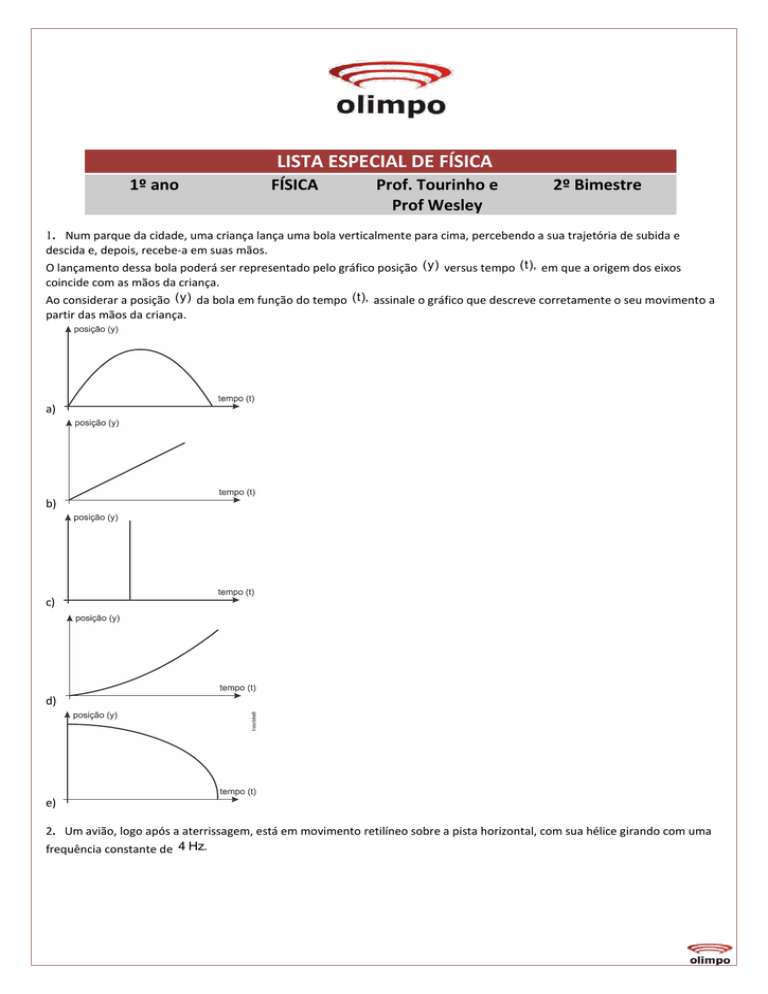
1. Num parque da cidade, uma criança lança uma bola verticalmente para cima, percebendo a sua trajetória de subida e
descida e, depois, recebe-a em suas mãos.
O lançamento dessa bola poderá ser representado pelo gráfico posição (y) versus tempo (t), em que a origem dos eixos
coincide com as mãos da criança.
Ao considerar a posição (y) da bola em função do tempo (t), assinale o gráfico que descreve corretamente o seu movimento a
partir das mãos da criança.
a)
b)
c)
d)
e)
2. Um avião, logo após a aterrissagem, está em movimento retilíneo sobre a pista horizontal, com sua hélice girando com uma
frequência constante de 4 Hz.
Considere que em um determinado intervalo de tempo a velocidade escalar desse avião em relação ao solo é constante e igual a
2 m s, que cada pá da hélice tem 1m de comprimento e que π 3. Calcule:
a) a distância, em metros, percorrida pelo avião enquanto sua hélice dá 12 voltas completas.
b) o módulo da velocidade vetorial instantânea, em m s, de um ponto da extremidade de uma das pás da hélice do avião, em
relação ao solo, em determinado instante desse intervalo.
3. A partir do repouso, um foguete de brinquedo é lançado verticalmente do chão, mantendo uma aceleração constante de
5,00 m s2 durante os 10,0 primeiros segundos. Desprezando a resistência do ar, a altura máxima atingida pelo foguete e o
tempo total de sua permanência no ar são, respectivamente, de
a) 375 m e 23,7 s.
b) 375 m e 30,0 s.
c) 375 m e 34,1s.
d) 500 m e 23,7 s.
e) 500 m e 34,1s.
4. Um balão dirigível sobe verticalmente, com velocidade constante de 90,0 km h em relação ao solo, e, a uma altura de
80,0 m do chão, um de seus passageiros arremessa um objeto com velocidade vertical e para cima de 18,0 km h, em relação
ao piso do cesto do balão. Em quantos segundos, o objeto retorna para a mão do passageiro?
a) 5,0
b) 4,0
c) 3,0
d) 2,0
e) 1,0
5. Dois objetos A e B de massas 400 g e 800 g, respectivamente, são lançados a partir do solo verticalmente para cima, ao
mesmo tempo e com velocidades iniciais idênticas.
Em um contexto no qual a resistência do ar é desprezada, analise as afirmativas que seguem.
I. O objeto A atingirá uma altura que será o dobro da atingida pelo objeto B.
II. A aceleração de A é a mesma de B.
III. O objeto A atingirá a altura máxima antes do objeto B.
IV. Os dois objetos gastarão o mesmo tempo para atingir a altura máxima.
Está correto apenas o que se afirma em:
a) II e IV.
b) I e IV.
c) III e IV.
d) I e II.
e) II e III.
6. Um corpo foi lançado verticalmente para cima com uma velocidade inicial V0 e após certo tempo ele alcança a altura
2
máxima HMAX . Desprezando o atrito do ar, e considerando g 10m / s , podemos afirmar que quando a sua velocidade foi
reduzida de um quinto (1/ 5) o corpo alcança uma altura, calculada em percentagem da altura HMAX , de
a) 15.
b) 25.
c) 50.
d) 46.
e) 36.
7. Em uma experiência de cinemática, estudantes analisaram o movimento de um objeto que foi lançado verticalmente para
cima a partir do solo. Eles verificaram que o objeto passa por um determinado ponto 0,5 s depois do lançamento, subindo, e
passa pelo mesmo ponto 3,5 s depois do lançamento, descendo. Considerando que essa experiência foi realizada em um local
2
onde a aceleração da gravidade é igual a 10 m s e que foram desprezadas quaisquer formas de atrito no movimento do
objeto, os estudantes determinaram que a velocidade de lançamento e altura máxima atingida pelo objeto em relação ao solo
são, respectivamente, iguais a:
a) 20 m s e 10 m
b) 20 m s e 20 m
c) 15 m s e 11,25 m
d) 15 m s e 22,50 m
8. Um objeto é lançado para baixo, na vertical, do alto de um prédio de 15 m de altura em relação ao solo. Desprezando-se a
resistência do ar e sabendo-se que ele chega ao solo com uma velocidade de 20 m / s, a velocidade de lançamento, em m / s, é
dada por
a) 10.
b) 15.
c) 20.
d) 25.
9. Maria brinca em um carrossel, que gira com velocidade constante. A distância entre Maria e o centro do carrossel é de
4,0 m. Sua mãe está do lado de fora do brinquedo e contou 20 voltas nos 10 min em que Maria esteve no carrossel.
Considerando essas informações, CALCULE:
a) A distância total percorrida por Maria.
b) A velocidade angular de Maria, em rad s.
c) O módulo de aceleração centrípeta de Maria.
10. Em uma obra de construção civil, uma carga de tijolos é elevada com uso de uma corda que passa com velocidade
constante de 13,5 m s e sem deslizar por duas polias de raios 27 cm e 54 cm. A razão entre a velocidade angular da polia
grande e da polia menor é
a) 3.
b) 2.
c) 2 3.
d) 1 2.
11.
Uma partícula percorre a trajetória circular de centro C e raio R. Os vetores velocidade (v) e aceleração (a) da partícula no
instante em que ela passa pelo ponto P da trajetória, estão representados na figura acima. O vetor velocidade e o vetor
m
aceleração formam um ângulo de 90. Se | v | 10,0 e R 2,00 m, o módulo da aceleração (| a |) será igual a
s
m
a) 4,00 2
s
m
b) 5,00 2
s
m
c) 20,00 2
s
m
d) 40,00 2
s
m
e) 50,00 2
s
12. Anemômetros são instrumentos usados para medir a velocidade do vento. A sua construção mais conhecida é a proposta
por Robinson em 1846, que consiste em um rotor com quatro conchas hemisféricas presas por hastes, conforme figura abaixo.
Em um anemômetro de Robinson ideal, a velocidade do vento é dada pela velocidade linear das conchas. Um anemômetro em
que a distância entre as conchas e o centro de rotação é r 25 cm, em um dia cuja velocidade do vento é v 18 km / h, teria
uma frequência de rotação de
Se necessário, considere π 3.
a) 3 rpm.
b) 200 rpm.
c) 720 rpm.
d) 1200 rpm.
13. Durante os festejos do Círio de Nazaré, em Belém, uma das atrações é o parque de brinquedos situado ao lado da Basílica,
no qual um dos brinquedos mais cobiçados é a Roda Gigante, que gira com velocidade angular ω, constante.
Considerando-se que a velocidade escalar de um ponto qualquer da periferia da Roda é V 1m s e que o raio é de 15 m,
pode-se afirmar que a frequência de rotação f, em hertz, e a velocidade angular ω, em rad s, são respectivamente iguais a:
a)
b)
c)
d)
e)
1
30π
1
15π
1
30π
1
15π
1
30π
2
15
2
e
15
1
e
15
1
e
15
1
e
30π
e
14. A figura abaixo representa um móvel m que descreve um movimento circular uniforme de raio R, no sentido horário, com
velocidade de módulo V.
Assinale a alternativa que melhor representa, respectivamente, os vetores velocidade V e aceleração a do móvel quando
passa pelo ponto I, assinalado na figura.
a)
b)
c)
d)
e)
15. Um automóvel desce uma rampa, com velocidade constante. Considere que o pneu tem diâmetro 60 cm e que gira sem
deslizar. Se o tempo para o pneu dar uma volta completa for 0,314 s, a velocidade do carro, em m s, é
a) 60 0,314.
b) 12.
c) 60.
d) 3,14.
16. Um pequeno motor a pilha é utilizado para movimentar um carrinho de brinquedo. Um sistema de engrenagens transforma
a velocidade de rotação desse motor na velocidade de rotação adequada às rodas do carrinho. Esse sistema é formado por
quatro engrenagens, A, B, C e D, sendo que A está presa ao eixo do motor, B e C estão presas a um segundo eixo e D a um
terceiro eixo, no qual também estão presas duas das quatro rodas do carrinho.
Nessas condições, quando o motor girar com frequência fM , as duas rodas do carrinho girarão com frequência fR . Sabendo que
as engrenagens A e C possuem 8 dentes, que as engrenagens B e D possuem 24 dentes, que não há escorregamento entre
elas e que fM 13,5 Hz, é correto afirmar que fR , em Hz, é igual a
a) 1,5.
b) 3,0.
c) 2,0.
d) 1,0.
e) 2,5.
17. A invenção e o acoplamento entre engrenagens revolucionaram a ciência na época e propiciaram a invenção de várias
tecnologias, como os relógios. Ao construir um pequeno cronômetro, um relojoeiro usa o sistema de engrenagens mostrado. De
acordo com a figura, um motor é ligado ao eixo e movimenta as engrenagens fazendo o ponteiro girar. A frequência do motor é
de 18 rpm, e o número de dentes das engrenagens está apresentado no quadro.
Engrenagem
Dentes
A
24
B
72
C
36
D
108
A frequência de giro do ponteiro, em rpm, é
a) 1.
b) 2.
c) 4.
d) 81.
e) 162.
18. Um astronauta, em um planeta desconhecido, observa que um objeto leva 2,0 s para cair, partindo do repouso, de uma
altura de 12 m.
A aceleração gravitacional nesse planeta, em m / s2 é:
a) 3,0
b) 6,0
c) 10
d) 12
e) 14
19. A castanha-do-pará (Bertholletia excelsa) é fonte de alimentação e renda das populações tradicionais da Amazônia. Sua
coleta é realizada por extrativistas que percorrem quilômetros de trilhas nas matas, durante o período das chuvas amazônicas. A
castanheira é uma das maiores árvores da floresta, atingindo facilmente a altura de 50m. O fruto da castanheira, um ouriço,
tem cerca de 1kg e contém, em média, 16 sementes. Baseando-se nesses dados e considerando o valor padrão da aceleração
2
da gravidade 9,81m / s , pode-se estimar que a velocidade com que o ouriço atinge o solo, ao cair do alto de uma castanheira,
é de, em m / s, aproximadamente,
a) 5,2.
b) 10,1.
c) 20,4.
d) 31,3.
e) 98,1.
20. Um corpo A é abandonado de um ponto situado a 10 metros acima do solo. No mesmo instante, um corpo B é lançado
verticalmente de baixo para cima com velocidade v 0 suficiente para que possa atingir 10 metros de altura.
Desprezando a resistência do ar, chamando respectivamente v A e vB as velocidades de A e B quando se encontram a 5
metros de altura, o valor da razão v A vB , em módulo é
a) 4
b) 2
c) 1
d) 1 2
21. Um paraquedista salta de um avião e cai livremente por uma distância vertical de 80m, antes de abrir o paraquedas.
2
Quando este se abre, ele passa a sofrer uma desaceleração vertical de 4m / s , chegando ao solo com uma velocidade vertical
de módulo 2m / s. Supondo que, ao saltar do avião, a velocidade inicial do paraquedista na vertical era igual a zero e
2
considerando g 10m / s , determine:
a) O tempo total que o paraquedista permaneceu no ar, desde o salto até atingir o solo.
b) A distância vertical total percorrida pelo paraquedista.
22. Vários corpos idênticos são abandonados de uma altura de 7,20m em relação ao solo, em intervalos de tempos iguais.
Quando o primeiro corpo atingir o solo, o quinto corpo inicia seu movimento de queda livre. Desprezando a resistência do ar e
2
adotando a aceleração da gravidade g 10,0 m / s , a velocidade do segundo corpo nessas condições é
a) 10,0 m / s
b) 6,0 m / s
c) 3,0 m / s
d) 9,0 m / s
e) 12,0 m / s
23. Considere um computador que armazena informações em um disco rígido que gira a uma frequência de 120 Hz. Cada
unidade de informação ocupa um comprimento físico de 0,2 μm na direção do movimento de rotação do disco. Quantas
informações magnéticas passam, por segundo, pela cabeça de leitura, se ela estiver posicionada a 3 cm do centro de seu eixo,
como mostra o esquema simplificado apresentado abaixo?
(Considere π 3.)
6
a) 1,62 10 .
6
b) 1,8 10 .
8
c) 64,8 10 .
8
d) 1,08 10 .
24. Um internauta brasileiro reside na cidade de Macapá situada sobre o equador terrestre a 0 de latitude. Um colega seu
reside no extremo sul da Argentina. Eles conversam sobre a rotação da Terra. Assinale a afirmativa CORRETA.
a) Quando a Terra dá uma volta completa, a distância percorrida pelo brasileiro é maior que a distância percorrida pelo
argentino.
b) O período de rotação para o argentino é maior que para o brasileiro.
c) Ao final de um dia, eles percorrerão a mesma distância.
d) Se essas pessoas permanecem em repouso diante de seus computadores, elas não percorrerão nenhuma distância no espaço.
25. Analise a figura abaixo.
Na figura acima temos um dispositivo A que libera partículas a partir do repouso com um período T 3 s. Logo abaixo do
dispositivo, a uma distância H, um disco contém um orifício que permite a passagem de todas as partículas liberadas pelo
dispositivo. Sabe-se que entre a passagem das duas partículas, o disco executa 3 voltas completas em torno de seu eixo. Se
elevarmos o disco a uma altura H 4 do dispositivo, qual das opções abaixo exibe o conjunto de três velocidades angulares w ',
em rad s, possíveis para o disco, de forma tal, que todas as partículas continuem passando pelo seu orifício?
Dado: considere π 3
a) 2 3, 5 3, e 8 3
b) 2, 3 e 5
c) 4 3, 8 3, e 12 3
d) 4, 7 e 9
e) 6, 8 e 12
26. Recentemente, foi instalada, em Passo Fundo, uma ciclovia para que a população possa andar de bicicleta. Imagine que, em
um final de semana, pai e filho resolveram dar uma volta, cada um com sua respectiva bicicleta, andando lado a lado, com a
mesma velocidade. Admitindo-se que o diâmetro das rodas da bicicleta do pai é o dobro do diâmetro das rodas da bicicleta do
filho, pode-se afirmar que as rodas da bicicleta do pai, em relação às da bicicleta do filho giram com:
a) o dobro da frequência e da velocidade angular.
b) a metade da frequência e da velocidade angular.
c) a metade da frequência e a mesma velocidade angular.
d) a mesma frequência e a metade da velocidade angular.
e) a mesma frequência e o dobro da velocidade angular.
27. Uma pessoa do alto de um prédio solta uma bola e mede o módulo da posição da bola em função do tempo. A figura,
abaixo, mostra o esboço do gráfico da posição em relação ao tempo.
Assinale a alternativa que representa o esboço dos gráficos em relação à velocidade tempo e à aceleração tempo,
respectivamente.
a)
b)
c)
d)
e)
28. Em um certo planeta, um corpo é atirado verticalmente para cima, no vácuo, de um ponto acima do solo horizontal. A
2
altura, em metros, atingida pelo corpo é dada pela função h(t) At Bt C, em que t está em segundos. Decorridos 4
segundos do lançamento, o corpo atinge a altura máxima de 9 metros e, 10 segundos após o lançamento, o corpo toca o solo.
A altura do ponto de lançamento, em metros, é
a) 0
b) 2
c) 3
d) 5
e) 6
29. As máquinas cortadeiras e colheitadeiras de cana-de-açúcar podem substituir dezenas de trabalhadores rurais, o que pode
alterar de forma significativa a relação de trabalho nas lavouras de cana-de-açúcar. A pá cortadeira da máquina ilustrada na
figura abaixo gira em movimento circular uniforme a uma frequência de 300 rpm. A velocidade de um ponto extremo P da pá
vale
(Considere π 3. )
a) 9 m/s.
b) 15 m/s.
c) 18 m/s.
d) 60 m/s.
30. Uma das modalidades de corridas de automóveis muito populares nos Estados Unidos são as corridas de arrancadas, lá
chamadas de Dragsters Races. Estes carros são construídos para percorrerem pequenas distâncias no menor tempo. Uma das
características destes carros é a diferença entre os diâmetros dos seus pneus dianteiros e traseiros. Considere um Dragster cujos
pneus traseiros e dianteiros tenham respectivamente diâmetros de d1 1,00 m e d2 50,00 cm.
Para percorrer uma distância de 300,00 m, a razão (n1 / n2 ), entre o número de voltas que os pneus traseiros e dianteiros,
supondo que em nenhum momento haverá deslizamento dos pneus com o solo, será:
a) 150,00
b) 50,00
c) 25,00
d) 2,00
e) 0,50
31. Um professor utiliza essa história em quadrinhos para discutir com os estudantes o movimento de satélites. Nesse sentido,
pede a eles que analisem o movimento do coelhinho, considerando o módulo da velocidade constante.
Desprezando a existência de forças dissipativas, o vetor aceleração tangencial do coelhinho, no terceiro quadrinho, é
a) nulo.
b) paralelo à sua velocidade linear e no mesmo sentido.
c) paralelo à sua velocidade linear e no sentido oposto.
d) perpendicular à sua velocidade linear e dirigido para o centro da Terra.
e) perpendicular à sua velocidade linear e dirigido para fora da superfície da Terra.
32. Em uma experiência didática, cinco esferas de metal foram presas em um barbante, de forma que a distância entre esferas
consecutivas aumentava em progressão aritmética. O barbante foi suspenso e a primeira esfera ficou em contato com o chão.
Olhando o barbante de baixo para cima, as distâncias entre as esferas ficavam cada vez maiores. Quando o barbante foi solto, o
som das colisões entre duas esferas consecutivas e o solo foi gerado em intervalos de tempo exatamente iguais.
A razão de os intervalos de tempo citados serem iguais é que a
a) velocidade de cada esfera é constante.
b) força resultante em cada esfera é constante.
c) aceleração de cada esfera aumenta com o tempo.
d) tensão aplicada em cada esfera aumenta com o tempo.
e) energia mecânica de cada esfera aumenta com o tempo.
33. Em um dia de calmaria, um garoto sobre uma ponte deixa cair, verticalmente e a partir do repouso, uma bola no instante t0
= 0 s. A bola atinge, no instante t4, um ponto localizado no nível das águas do rio e à distância h do ponto de lançamento. A
figura apresenta, fora de escala, cinco posições da bola, relativas aos instantes t 0, t1, t2, t3 e t4. Sabe-se que entre os instantes t2 e
2
t3 a bola percorre 6,25 m e que g = 10 m/s .
Desprezando a resistência do ar e sabendo que o intervalo de tempo entre duas posições consecutivas apresentadas na figura é
sempre o mesmo, pode-se afirmar que a distância h, em metros, é igual a
a) 25.
b) 28.
c) 22.
d) 30.
e) 20.
34. Para serrar ossos e carnes congeladas, um açougueiro utiliza uma serra de fita que possui três polias e um motor. O
equipamento pode ser montado de duas formas diferentes, P e Q. Por questão de segurança, é necessário que a serra possua
menor velocidade linear.
Por qual montagem o açougueiro deve optar e qual a justificativa desta opção?
a) Q, pois as polias 1 e 3 giram com velocidades lineares iguais em pontos periféricos e a que tiver maior raio terá menor
frequência.
b) Q, pois as polias 1 e 3 giram com frequências iguais e a que tiver maior raio terá menor velocidade linear em um ponto
periférico.
c) P, pois as polias 2 e 3 giram com frequências diferentes e a que tiver maior raio terá menor velocidade linear em um ponto
periférico.
d) P, pois as polias 1 e 2 giram com diferentes velocidades lineares em pontos periféricos e a que tiver menor raio terá maior
frequência.
e) Q, pois as polias 2 e 3 giram com diferentes velocidades lineares em pontos periféricos e a que tiver maior raio terá menor
frequência.
35. Um objeto é abandonado do alto de um prédio de altura 80 m em t = 0. Um segundo objeto é largado de 20 m em t = t 1.
Despreze a resistência do ar.
Sabendo que os dois objetos colidem simultaneamente com o solo, t 1 vale:
2
Considere g = 10 m/s .
a) 1,0 s.
b) 2,0 s.
c) 3,0 s.
d) 4,0 s.
e) 5,0 s.
36. Um caminhão de carga tem rodas dianteiras de raio Rd 50 cm e rodas traseiras de raio Rt 80 cm. Em determinado
trecho do trajeto plano e retilíneo, percorrido sem deslizar e com velocidade escalar constante, a frequência da roda dianteira é
igual a 10 Hz e efetua 6,75 voltas a mais que a traseira.
Considerando π 3, determine:
a) A velocidade escalar média do caminhão, em km h.
b) A distância percorrida por ele nesse trecho do trajeto.
37. Uma pedra A é lançada para cima com velocidade inicial de 20 m/s. Um segundo antes, outra pedra B era largada de uma
altura de 35 m em relação ao solo. Supondo o atrito com o ar desprezível, no instante em que elas se encontram, é correto
afirmar que:
01) a aceleração da pedra A tem sentido oposto à aceleração da pedra B.
02) o módulo da velocidade da pedra B é de 20 m/s.
04) o módulo da velocidade da pedra A é de 10 m/s.
08) a distância percorrida pela pedra A é de 16 m.
16) a posição da pedra B em relação ao solo é de 20 m.
38. Uma esfera de dimensões desprezíveis é largada, a partir do repouso, de uma altura igual a 80 m do solo considerado
horizontal e plano. Desprezando-se a resistência do ar e considerando-se a aceleração da gravidade constante e igual a
10 m / s2 , é correto afirmar-se que a distância percorrida pela esfera, no último segundo de queda, vale
a) 20 m.
b) 35 m.
c) 40 m.
d) 45 m.
e) 55 m.
39. Três bolinhas idênticas, são lançadas na vertical, lado a lado e em sequência, a partir do solo horizontal, com a mesma
velocidade inicial, de módulo igual a 15 m/s para cima. Um segundo após o lançamento da primeira, a segunda bolinha é
lançada. A terceira bolinha é lançada no instante em que a primeira, ao retornar, toca o solo.
2
Considerando g = 10 m/s e que os efeitos da resistência do ar ao movimento podem ser desprezados, determine
a) a altura máxima (hmax) atingida pela primeira bolinha e o instante de lançamento da terceira bolinha.
b) o instante e a altura H, indicada na figura, em que a primeira e a segunda bolinha se cruzam.
40. Uma bola cai em queda livre a partir do repouso. Quando a distância percorrida for h, a velocidade será v1 . Quando a
v2
distância percorrida for 16h a velocidade será v 2 . Calcule a razão v . Considere desprezível a resistência do ar.
1
41. Uma pedra, partindo do repouso, cai verticalmente do alto de um prédio cuja altura é “h”. Se ela gasta um segundo (1s)
para percorrer a última metade do percurso qual é o valor em metros (m) que melhor representa a altura “h” do prédio?
2
Desconsidere o atrito com o ar, e considere o módulo da aceleração da gravidade igual a 9,8 m s .
a) 80,6 m
b) 100,2 m
c) 73,1 m
d) 57,1 m
e) 32,0 m
42. Em um local onde g 10m / s , um objeto é lançado verticalmente para cima, a partir do solo terrestre. O efeito do ar é
desprezível.
O objeto atinge 20% de sua altura máxima com uma velocidade de módulo igual a 40 m/s. A altura máxima atingida pelo objeto
vale:
a) 200 m
b) 150 m
c) 100 m
d) 75 m
2
43. Numa pista circular de diâmetro 200 m, duas pessoas se deslocam no mesmo sentido, partindo de pontos diametralmente
opostos da pista. A primeira pessoa parte com velocidade angular constante de 0,010 rad/s, e a segunda parte,
simultaneamente, com velocidade escalar constante de 0,8 m/s.
As duas pessoas estarão emparelhadas após (use π com duas casas decimais)
a) 18 minutos e 50 segundos.
b) 19 minutos e 10 segundos.
c) 20 minutos e 5 segundos.
d) 25 minutos e 50 segundos.
e) 26 minutos e 10 segundos.
TEXTO PARA A PRÓXIMA QUESTÃO:
Nesta prova adote os conceitos da Mecânica Newtoniana e as seguintes convenções:
2
O valor da aceleração da gravidade: g = 10 m/s .
O valor π = 3.
A resistência do ar pode ser desconsiderada.
44. Na modalidade de arremesso de martelo, o atleta gira o corpo juntamente com o martelo antes de arremessá-lo. Em um
treino, um atleta girou quatro vezes em três segundos para efetuar um arremesso. Sabendo que o comprimento do braço do
atleta é de 80 cm, desprezando o tamanho do martelo e admitindo que esse martelo descreve um movimento circular antes de
ser arremessado, é correto afirmar que a velocidade com que o martelo é arremessado é de:
a) 2,8 m/s
b) 3,0 m/s
c) 5,0 m/s
d) 6,4 m/s
e) 7,0 m/s
TEXTO PARA A PRÓXIMA QUESTÃO:
Um objeto é lançado da superfície da Terra verticalmente para cima e atinge a altura de 7,2 m.
(Considere o módulo da aceleração da gravidade igual a 10 m / s2 e despreze a resistência do ar.)
45. Sobre o movimento do objeto, são feitas as seguintes afirmações.
I. Durante a subida, os vetores velocidade e aceleração têm sentidos opostos.
II. No ponto mais alto da trajetória, os vetores velocidade e aceleração são nulos.
III. Durante a descida, os vetores velocidade e aceleração têm mesmo sentido.
Quais estão corretas?
a) Apenas I.
b) Apenas II.
c) Apenas I e II.
d) Apenas I e III.
e) Apenas II e III.
Gabarito:
Resposta da questão 1:
[A]
A posição em função do tempo de um objeto em lançamento vertical varia quadraticamente, indicando o gráfico de uma
parábola, sendo o movimento de subida retardado e a descida acelerado. O movimento é retilíneo uniformemente retardado na
subida até a altura máxima atingida pelo objeto e a descida passa a ser acelerada sendo em ambos os trechos a aceleração igual
à da gravidade.
Resposta da questão 2:
Dados: fhel 4 Hz; vav 2 m s; hel 1m; π 3.
a) O tempo gasto pela hélice para realizar 12 voltas completas corresponde a:
1
Δt 12T 12
fhel
1
sendo T f
o período de cada ciclo da hélice.
hel
Substituindo na equação os valores de parâmetros conhecidos, tem-se que:
12 12
Δt
3s
fhel
4
A distância percorrida pelo avião no intervalo de tempo Δt 3 s, é:
ΔS vav Δt 2 3 6 m
b) A velocidade vetorial instantânea da extremidade de uma das hélices será uma composição da velocidade da extremidade da
hélice relativa ao avião, v t , e a velocidade do avião em relação ao solo, v av :
lembrando que o símbolo na segunda figura representa um vetor perpendicular ao plano do papel, "saindo" do mesmo.
Da composição vetorial, conclui-se que
v 2 v t 2 vav 2 v v t 2 vav 2
A velocidade do avião v av possui módulo conhecido e igual a 2 m s.
A velocidade v t , ou melhor, o seu módulo, é obtido da seguinte forma:
v t ω hel 2 π fhel hel 2 3 4 1 24 m s
Substituindo-se os parâmetros conhecidos na equação do módulo da velocidade total, obtém-se:
v 242 22 242 24 m s
Resposta da questão 3:
[A]
H0 0 m
t1 10 s
a1 5 m s2
a2 g 10 m s2
2
1ª etapa: foguete sobe do chão durante 10 s com aceleração de 5 m s .
1
H1 H0 Vo t a1t12
2
5
H1 102 H1 250 m (i)
2
V1 V0 a1t1
V1 50 m / s
(ii)
2ª etapa: foguete continua subindo com desaceleração da gravidade até atingir a altura máxima H2 .
V22 V12 2a2 (H2 H1)
0 502 2 ( 10) (H2 250)
H2 375 m
(iii)
V2 V1 a2 (t 2 t1)
0 50 ( 10) (t 2 10)
t2 5 s
(iv)
Depois dos 10 s subindo, o foguete subiu por mais 5 s, até adquirir velocidade zero.
3ª etapa: Foguete desce com aceleração da gravidade.
1
H3 H2 V2 Δt a Δt 2
2
0 375 0 5t 32
t3 8,7 s
t t t1 t 2 t3 t t 10 5 8,7 t t 23,7 s
Portanto, conforme indica a alternativa [A], a altura máxima atingida será de 375 m e o tempo total de 23,7 s.
Resposta da questão 4:
[E]
1ª opção:
Ajustando as velocidades em relação ao solo no Sistema Internacional de Unidades:
1m / s
Balão: vb 90 km / h 3,6 km / h 25 m / s
1m / s
Objeto: v0 18 90 km / h 3,6 km / h 30 m / s
Tomando as velocidades em relação ao solo, as equações das posições dos móveis em relação ao tempo são:
Balão: h 80 25t (1)
2
Objeto: h 80 30t 5t (2)
Para que o objeto retorne à mão do passageiro é necessário que a posição indicada pelo balão seja a mesma do objeto,
portanto, fazendo a igualdade das duas equações:
80 25t 80 30t 5t 2
25t 30t 5t 2
5t 2 5t 0
t2 t 0
t t 1 0
Resolvendo a equação de segundo grau incompleta, as raízes são:
t ' 0 s e t '' 1 s.
Logo, após o lançamento, o objeto retorna ao passageiro em apenas 1 segundo.
2ª opção:
Considerando o balão como um sistema inercial, usamos somente a informação do objeto efetuando um lançamento vertical
com velocidade inicial referida ao balão.
1m / s
Objeto: v0 18 km / h 3,6 km / h 5 m / s
Usando a equação horária da velocidade para o lançamento vertical, v v 0 gt.
Sabendo-se que a velocidade final terá sentido contrário da velocidade inicial, mas de mesmo módulo e usando a aceleração da
2
gravidade g 10 m / s :
5 5 10t t 1 s
Resposta da questão 5:
[A]
[I] Falsa. Sendo as velocidades iniciais iguais e cada um tendo como aceleração a gravidade, ambas vão atingir a altura máxima e
chegar ao solo ao mesmo tempo.
[II] Verdadeira. Ambos estão sujeitos à ação da gravidade.
[III] Falsa. Como já mencionado em [I], os dois corpos chegam juntos na altura máxima.
[IV] Verdadeira. Os movimentos são idênticos.
Resposta da questão 6:
ANULADA
Gabarito Oficial: [E]
Gabarito SuperPro®: Anulada.
Para os dois lançamentos do mesmo ponto, considerando primeiramente o lançamento para a altura máxima:
HMAX V0 t
g 2
t
2
Mas na altura máxima, a velocidade neste ponto é nula, então o tempo de subida pode ser colocado em termos da velocidade
inicial.
V
V V0 g t 0 V0 g t t 0
g
Substituindo o tempo na equação anterior, temos:
2
V
V2
g V
HMAX V0 0 0 HMAX 0
g 2 g
2g
A velocidade para o segundo lançamento foi reduzida de um quinto (1/ 5) : :
V
4V0
V0 ' V0 0
5
5
Para o lançamento com menor velocidade:
4V0
g
H
t ' t ' 2
5
2
Da mesma forma, na altura máxima para esse lançamento, a velocidade é nula neste ponto:
4V0
4V0
4V0
V
g t' 0
g t't'
5
5
5g
Substituindo na expressão da altura:
H
4V0 4V0 g 4V0 2
16V02 16V02
16V02
H
H
5
5g 2 5g
25g
50g
50g
Finalmente, dividindo as duas expressões das alturas:
H
HMAX
16V02
50g
2
V0
2g
H
HMAX
32
H
0,64
50 HMAX
Logo, a altura do segundo lançamento chega a 64% do primeiro, tendo assim, uma questão sem alternativa correta e, portanto
devendo ser ANULADA.
Observação: Se fosse perguntado a diferença em percentual entre os dois lançamentos ou ainda se a velocidade inicial fosse
reduzida à um quinto teríamos a resposta correta como indicada pela banca.
Resposta da questão 7:
[B]
Como, em relação à mesma horizontal, o tempo de subida é igual ao de descida, o tempo total de movimento é 4 segundos;
então o tempo de descida, em queda livre, é 2 segundos. Aplicando as equações da queda livre:
v 20 m/s.
v gt 10 2
g 2 10 2
2 h 20 m.
h t
2
2
Resposta da questão 8:
[A]
2
Dado: v 20m s; h 15m; g 10 m s .
Aplicando a equação de Torricelli:
v 2 v 02 2gh v 0
v 2 2gh
202 2 10 15
100
v 0 10 m s.
Resposta da questão 9:
a) A distância percorrida é igual ao número de voltas (n) vezes o comprimento de cada volta.
d n2π R 20 2π 4
b) ω
n2π 20 2π
Δt
10 60
d 160π m .
ω
π
rad/s.
15
2
4 π2
π
2
c) ac ω R 4
225
15
ac 0,018 π2 m/s2 .
Resposta da questão 10:
[D]
A velocidade linear é a mesma para as duas polias.
v G vM ω G R G ω M R M
ωG
ωM
RM
RG
27
54
ωG
ωM
1
.
2
Resposta da questão 11:
[E]
O módulo da aceleração centrípeta é dado por:
ac
v2
R
Assim, teremos:
ac
10 m s 2
2m
ac 50 m s2
Resposta da questão 12:
[B]
Dados: v 18 km/h 5 m/s; r 25 cm 0,25 m; π 3.
v 2 πr f f
v
5
5
5
Hz
60 rpm
2 π r 2 3 0,25 1,5
1,5
Resposta da questão 13:
[C]
V 2 πR f f
ω 2πf 2π
V
1
2 π R 2 π 15
1
30 π
Resposta da questão 14:
ω
1
rad/s.
15
f
1
Hz.
30 π
f 200 rpm.
[C]
No movimento circular uniforme (MCU) a velocidade é representada por um vetor tangente ao círculo em cada ponto ocupado
pelo móvel, com isto, apesar do módulo da velocidade permanecer constante, ao longo do movimento o vetor velocidade altera
sua direção e sentido, sendo, portanto, um movimento acelerado em que a aceleração é sempre perpendicular ao vetor
velocidade apontando para o centro da curva, chamada de aceleração centrípeta. Assim, a alternativa correta é a [C].
Resposta da questão 15:
ANULADA
Questão anulada no gabarito oficial.
Dados: D 60cm 0,6m; T 0,314s.
ΔS π D 3,14 0,6
v
v 6m/s.
Δt
T
0,314
Resposta da questão 16:
[A]
Os raios das engrenagens (R) e os números de dentes (n) são diretamente proporcionais. Assim:
RA RC nA
8
1
.
RB RD nB 24 3
- A e B estão acopladas tangencialmente:
v A v B 2 π fA R A 2 π f B R B f A R A f B R B .
R
1
fB fM A fM
RB
3
Mas : fA f M f M R A f B R B
fB
fM
3
.
- B e C estão acopladas coaxialmente:
fM
fC f B
.
3
- C e D estão acopladas tangencialmente:
v C vD 2 π f C R C 2 π f D R D fC RC f D R D .
Mas : f D f R f C RC f R R D
FR
13,5
9
fM 1
R
fR fC C fR
RD
3 3
fR
fM
9
f R 1,5 Hz.
Resposta da questão 17:
[B]
No acoplamento coaxial as frequências são iguais. No acoplamento tangencial as frequências (f) são inversamente
proporcionais aos números (N) de dentes;
Assim:
fA fmotor 18 rpm.
fB NB fA NA fB 72 18 24 fB 6 rpm.
fC fB 6 rpm.
f N f N f 108 6 36 f 2 rpm.
D
D
D D C C
A frequência do ponteiro é igual à da engrenagem D, ou seja:
f 2 rpm.
Resposta da questão 18:
[B]
Com a equação da altura em função do tempo do movimento de queda livre, calculamos a aceleração.
gt 2
2h
g
2
t2
2 12 m
g
6 m / s2
2
2
s
h
Resposta da questão 19:
[D]
Aplicando a equação de Torricelli à queda livre, temos:
v2 2 gh v
2 g h 2 9,81 50
981
v 31,3 m/s.
Resposta da questão 20:
[C]
Temos situações semelhantes para os dois corpos, pois ambos percorrem 5 m com as mesmas acelerações sendo que as
condições de contorno também são similares, logo as velocidades em módulo serão iguais e sua razão será 1.
Outra possibilidade é calcular usando os conhecimentos de lançamento vertical e queda livre.
Para o corpo A, que cai em queda livre, usando o referencial positivo para baixo e a equação de Torricelli:
v 2 v02 2gΔh v v02 2gΔh
v A 02 2 10 5 v 10 m / s
Para o corpo B, que sobe na vertical, usando o referencial positivo para cima, primeiramente descobrimos a velocidade inicial e
depois a velocidade na posição de 5 m :
v 2 v02 2gΔh v0 v 2 2gΔh
v0 02 2 10 10 v0 10 2 m s
E a intensidade da velocidade a 5 m de altura:
vB
10 2
2
2 10 5 v 10 m / s
v A 10
Então, v 10 1.
B
Resposta da questão 21:
a) Tempo total do salto até atingir o solo: t t1 t 2
No primeiro momento, na queda livre do paraquedista.
ΔS1 v o t
80
a t12
2
10 t12
2
t12 16
t1 4 s
Encontrando a velocidade no final do primeiro momento,
v1 v o a t1
v1 10 4
v1 40 m s
Assim, achando o tempo do segundo momento, temos que:
v 2 v1 a t 2
2 40 4 t 2
t 2 9,5 s
Por fim, o tempo total será:
t t1 t 2 4 9,5
t 13,5 s
b) A distância total percorrida: ΔSt ΔS1 ΔS2
A distância percorrida no primeiro momento foi dada no enunciado (80 m). Para o segundo momento, temos que:
v 22 v12 2 a ΔS2
22 402 2 4 ΔS2
402 22
8
ΔS2 199,5 m
Δ S2
Logo,
ΔSt 80 199,5
ΔSt 279,5 m
Resposta da questão 22:
[D]
Calculando o tempo de queda:
h
1 2
g t q tq
2
2h
g
2 7,2
10
1,44 t q 1,2 s.
A figura mostra os cinco corpos e o tempo (t) de movimento de cada um deles.
A velocidade do 2º corpo é:
v v0 g t v 0 10 0,9
v 9 m/s.
Resposta da questão 23:
[D]
- Espaço ocupado por cada informação:
L 0,2 μm 2 107 m.
- Comprimento de uma volta:
C 2 π r 2 3 3 102 18 102 m.
- Número de informações armazenadas em cada volta:
n
C 18 102
9 105.
L
2 107
- Como são 120 voltas por segundo, o número de informações armazenadas a cada segundo é:
N n f 9 105 120
N 1,08 108.
Resposta da questão 24:
[A]
Em relação ao eixo de rotação da Terra, o raio da trajetória seguida pelo argentino (r) em relação a esse eixo é menor que o raio
da trajetória seguida pelo brasileiro (R), na linha do equador. Após uma volta completa as distâncias percorridas são:
Argentino : dA 2 π r
Brasileiro: dB 2 π R
Rr
dB dA .
Resposta da questão 25:
[E]
Observação: suponha-se que o disco execute 3 voltas completas entre as passagens de duas bolinhas consecutivas.
Independente da altura de queda, passada uma bolinha, a próxima passa depois de 3 segundos. Assim, para que ocorra o
proposto, o disco deve executar, no mínimo, 1 volta a cada 3 s, ou voltas inteiras a partir desse valor. Portanto as frequências
possíveis são:
1 2 3 4 5 6
f , , , , , ,... Hz.
3 3 3 3 3 3
Sendo ω 2 π f, fazendo π 3, as possíveis velocidades angulares são:
1 2 3 4 5 6
ω 2 3 , , , , , ,... ω 2, 4, 6 , 8 , 10, 12 , 14,... rad/s.
3 3 3 3 3 3
Resposta da questão 26:
[B]
A velocidade das rodas em função da frequência é dada pelo produto da distância percorrida em uma volta completa
(circunferência das rodas) e a frequência.
v 2πRf πDf
Igualando as velocidades do pai (1) e do filho (2), temos:
v1 v 2
π D1 f1 π D2 f2
Como o diâmetro das rodas da bicicleta do filho é a metade das rodas da bicicleta do pai:
D
π D1 f1 π 1 f2
2
Simplificando,
f
f1 2
2
Conclui-se que a frequência de giro das rodas da bicicleta do pai é a metade em relação a do filho.
Com relação à velocidade angular, partimos da sua relação com a velocidade linear:
v ωR
Como as velocidades do pai (1) e do filho (2) são iguais:
ω1 R1 ω2 R2
Dado que:
R
R2 1
2
R
ω1 R1 ω2 1
2
ω2
ω1
2
Encontramos a relação entre as velocidades angulares, com a bicicleta do pai sendo a metade da bicicleta do filho.
Resposta da questão 27:
[A]
Considerando desprezível a resistência do ar, a bola desce em queda livre até que, num determinado instante, ela para
abruptamente.
Assim, a velocidade escalar aumenta linearmente com o tempo, anulando-se instantaneamente, enquanto que a aceleração
escalar é constante, até se anular, também, instantaneamente, como mostram os gráficos da alternativa [A].
Resposta da questão 28:
[D]
Para um lançamento vertical com referencial no solo e trajetória orientada para cima, as funções horárias da altura e da
velocidade são:
g 2
h t t v 0 t h0
2
v t v g t
0
2
Comparando com a equação dada, h(t) At Bt C, temos:
g
A 2 g 2 A
v 0 B
h C
0
A função horária da velocidade em termos dos parâmetros dados fica:
v t B 2 A t v t B 2 A t.
No instante t = 4 s, o corpo atinge o ponto mais alto, sendo nula a velocidade na altura de 9 m. Assim:
v 4 0 B 2 A 4 0 B 8 A .
2
h 4 9 A 4 8 A 4 C 9 16 A C 9. I
No instante t = 10 s, o corpo atinge o solo (h = 0). Assim:
h 10 0 A 10 8 A 10 C 0 20 A C 0 A
2
C
20
II.
Substituindo (II) em (I):
180
C
16
C 9 16 C 20 C 180 C
36
20
C 5 m.
Resposta da questão 29:
[C]
Dados: f = 300 rpm = 5 Hz; π = 3; R = 60 cm = 0,6 m.
A velocidade linear do ponto P é:
v ω R 2 f R 2 3 5 0,6
v 18 m/s.
Resposta da questão 30:
[E]
Nota: a construção do segundo parágrafo está confusa. Deveria ser:
"Para percorrer uma distância de 300,00 m, a razão (n1 / n2 ), entre os números de voltas que os pneus traseiros e dianteiros
efetuam, supondo...".
Para qualquer distância percorrida (D), a razão entre os números de voltas dadas é a mesma.
D n1 2 π d1
n1 d 2 0,5
n1 2 π d1 n2 2 π d 2
D
n
2
π
d
n2 d1
1
2
2
n1
0,5.
n2
Resposta da questão 31:
[A]
Como o módulo da velocidade é constante, o movimento do coelhinho é circular uniforme, sendo nulo o módulo da componente
tangencial da aceleração no terceiro quadrinho.
Resposta da questão 32:
[B]
A questão está mal formulada.
Tratando-se de uma queda livre, independente do que diz o restante do enunciado, a única alternativa correta é a assinalada,
[B].
Além disso, o enunciado pode levar a entender que para qualquer razão da referida PA entre as distâncias consecutivas, os
intervalos de tempo sejam iguais, o que não é verdade.
Os intervalos de tempo somente são iguais se a razão da PA entre essas distâncias for 2 h, sendo h a altura em que se encontra a
2ª esfera (B), uma vez que a 1ª (A) está em contato com o solo, conforme ilustra a figura, fora de escala.
Da equação da queda livre, calculamos o tempo de queda de cada uma das esferas, B, C, D e
E.
t queda
tB
t
C
2H
g
tD
tE
2h
g
8h
2
g
2h
g
18 h
3
g
2h
g
32 h
4
g
2h
g
O intervalo de tempo entre dois sons consecutivos de uma esfera batendo sobre a outra é igual ao tempo de queda da esfera B:
Δt
2h
.
g
Resposta da questão 33:
[E]
1ª Solução:
De acordo com a “Regra de Galileo”, em qualquer Movimento Uniformemente Variado (MUV), a partir do repouso, em
intervalos de tempo iguais e consecutivos(Δt1, Δt 2 , ..., Δt n )a partir do início do movimento, as distâncias percorridas são: d;
3 d; 5 d; 7 d;...;(2 n – 1) d, sendo d, numericamente, igual à metade da aceleração. A figura ilustra a situação.
Dessa figura:
6,25
d 1,25 m.
5
h 16 d h 16 1,25 h 20 m.
5 d 6,25 d
2ª Solução
Analisando a figura, se o intervalo de tempo Δt entre duas posições consecutivas quaisquer é o mesmo, então:
t2 2 t; t3 3 t e t3 4 t.
Aplicando a função horária do espaço para a queda livre até cada um desses instantes:
1
1
S
g t 2 S 10 t 2 S 5 t 2 .
2
2
S 5 t 2
2
2
2
S3 5 t3
S2 5 2 Δt
2
S2 20 Δt 2
S3 5 3 Δt
2
2
S3 45 Δt
S3 S2 25 Δt 2 6,25 25 Δt 2
Δt 2 0,25.
Aplicando a mesma expressão para toda a queda:
h 5 t 24
h 5 4 Δt
2
h 80 Δt 2 80 0,25
h 20 m.
Resposta da questão 34:
[A]
A velocidade linear da serra é igual à velocidade linear (v) de um ponto periférico da polia à qual ela está acoplada.
Lembremos que no acoplamento tangencial, os pontos periféricos das polias têm mesma velocidade linear; já no acoplamento
coaxial (mesmo eixo) são iguais as velocidades angulares (ω), frequências (f) e períodos (T) de todos os pontos das duas polias.
Nesse caso a velocidade linear é diretamente proporcional ao raio (v = ω R).
Na montagem P:
– Velocidade da polia do motor: v1.
– Velocidade linear da serra: v3P.
v 3P ω3P R3
ω2P ω3P
v 2P
ω2P
R2
v v
1
2P
v 3P
v1 R3
R2
.
v 3P ω2P R3
I
Na montagem Q:
– Velocidade da polia do motor: v1.
– Velocidade linear da serra: v2Q.
v 3P
v 2P
R2
R3
v 2Q ω2Q R2
ω2Q ω3Q
v 3Q
ω3Q
R3
v
3Q v1
v 2Q
v1 R2
R3
v 2Q ω3Q R2 v 2Q
v 3Q
R3
R2
II
.
Dividindo (II) por (I):
v 2Q
v 3P
v1 R2
R3
R2
v1 R3
2
R
2 .
v 3P R3
v 2Q
Como R2 R3 v 2Q v3P.
Quanto às frequências, na montagem Q:
f
R
v3Q v1 f3Q R3 f1 R1 3Q 1 .
f1
R3
Como R1 R3 f3Q F1.
Resposta da questão 35:
[B]
Chamemos os objetos de A e de B. O tempo t1 pedido é a diferença entre os tempos de queda, tA e tB, respectivamente.
Para obter a expressão do tempo de queda, usamos a função horária do espaço.
2 80
16 t A 4 s
t A
2 H
1
10
H g t 2q t q
t1 t A tB 4 2
2
g
2 20
4 tB 2 s
tB
10
t1 2 s.
Resposta da questão 36:
a) v 2πRf, para a roda dianteira, temos:
v 2.3.0,5.10 30m / s , convertendo para km/h (multiplicando por 3,6),
v 108km / h
b) Como podemos perceber, o enunciado não fornece o tempo para a roda dianteira efetuar 6,75 voltas a mais que a traseira,
porém, sabemos que o deslocamento das rodas são iguais, assim temos:
ΔST ΔSD
n.2π.RT (n 6,75).2π.RD em que “n” representa do número de rotações da roda traseira.
Logo:
n.0,8 (n 6,75).0,5
0,8n 0,5n 3,375
0,3n 3,375
3375
n
11,25
300
Logo:
ΔST n.2π.RT
ΔST 11,25.2.3.0,8
ΔST 54m
Resposta da questão 37:
02 + 04 = 06
Vamos supor que a pedra A tenha sido lançada do solo, onde se adota o referencial, com trajetória orientada para cima.
Analisando cada uma das proposições:
01) Incorreta: a aceleração de ambas as pedras é a aceleração da gravidade local, a = -g.
02) Correta: como a pedra B é largada 1 segundo antes, seu tempo de movimento é t + 1, em relação à pedra A.
Adotando referencial no solo, as equações das alturas das pedras são:
1
hA h0A v 0A t a t 2 hA 20 t 5 t 2
2
h h v t 1 1 a t 12 h 35 5 t 12
B
0B
0B
B
2
Para calcular o instante de encontro, igualamos as duas equações:
20 t 5 t 2 35 5 t 1
30 t 30
2
20 t 5 t 2 35 5 t 2 10 t 5
t 1 s.
A velocidade da pedra B nesse instante é:
vB v 0B g t 1
vB 10 1 1
v B 20 m / s.
Em módulo:
vB 20m / s .
04) Correta: v A v 0A g t 20 10 1
v A 10 m / s.
08) Incorreta: até o instante de encontro, a distância percorrida pela pedra A é:
SA
1 2
2
g t 5 1
2
SA 5 m.
16) Incorreta: a posição da pedra B no instante de encontro é:
hB 35 5 1 1 15 m.
2
Resposta da questão 38:
[B]
Calculando o tempo de queda:
h
g t2
2
2h
2 80
4 s.
g
10
t
O último segundo de queda corresponde ao intervalo de 3 a 4 segundos. Sendo a velocidade inicial nula, calculemos as
velocidades nesses instantes:
v 3 10 3 30 m / s;
v v0 g t
v 4 10 4 40 m / s.
Aplicando a equação de Torricelli nesse intervalo:
v 24 v 32 2 g S
402 302 20 S
1.600 900 700
20
20
S 35 m.
S
Resposta da questão 39:
2
Dados: v0 = 15 m/s; a = –g = –10 m/s .
a) Aplicando a equação de Torricelli:
v 2 v02 2 a ΔS
v 2 v02 2 g h .
No ponto mais alto, a velocidade se anula e a altura é igual à altura máxima.
02 152 20 hmáx
hmáx
225
20
hmáx = 11,25 m.
O instante de lançamento da terceira bolinha (t3) é o instante em que a primeira bolinha atinge o solo, tempo total dessa
bolinha. Calculemos esse tempo (tT).
Da função horária da velocidade:
v v0 g t
v 15 10 t .
No ponto mais alto a velocidade se anula e o tempo é tempo de subida (tsub). Então:
0 15 10 t sub
t sub 1,5 s.
O tempo total é o dobro do tempo de subida. Assim:
t3 t T 2 t sub 2 1,5 t3 = 3 s.
b) Como a segunda bolinha é lançada 1 s depois, seu tempo de movimento é (t –1). Assim, da equação horária do espaço, as
equações das alturas para as duas bolinhas são:
g 2
h1 15 t 5 t 2 (I)
h1 v 0 t 2 t
g
2
2
h2 15 t 1 5 t 1
h2 v 0 t 1 t 1
2
2
h2 25 t 5 t 20 (II)
Igualando (I) e (II):
2
2
15 t – 5 t = 25 t – 5 t – 20 10 t = 20 t = 2 s.
Substituindo esse valor em I e II:
h 15 2 5 2 2 30 20 h 10 m
1
1
2
h2 15 2 1 5 2 1 15 5 h2 10 m
H 10 m.
Resposta da questão 40:
A queda livre é um MUV. Vale então a equação de Torricelli.
2
v 2 2gh
v2
v
1
2gh
1
V 2 V02 2.a.S 2
1
v 4
2g.16h 16
1
v 2 2g.16h
v2
Resposta da questão 41:
[D]
Supondo que ele gasta “t” segundos para efetuar a queda toda, a primeira metade foi percorrida em “(t – 1)” segundos. Sendo
assim:
1 2
gt
1 2
2
2
2
2
2
gt g(t 1) t 2t 4t 2 t 4t 4 0
h 1
2
g(t 1)2
2 2
h
t
t 3,4s
4 16 4x1x2 4 2 2
2 2
2
2
t 0,6s
O tempo deve ser maior que 1. Portanto, t = 3,4s.
1
1
h gt 2 x9,8x3,42 57m .
2
2
Resposta da questão 42:
[C]
A figura mostra o movimento do corpo:
Aplicando Torricelli, vem:
V 2 V02 2aΔS 0 402 2x10x0,8H 16H 1600 H 100m .
Resposta da questão 43:
[E]
Dados: D = 200 m r = 100 m; 2 0,01 rad/s; 3,14 .
A velocidade da pessoa mais rápida é:
v 2 2r 0,01 100 1 m / s.
Como partem de pontos diametralmente opostos, a distância (d) entre eles é meia volta. d r 3,14 100 314 m.
A pessoa mais rápida leva vantagem (velocidade relativa v rel ) de 0,2 m/s.
O tempo para tirar essa diferença é:
t
d
314
1570 s
v rel 0,2
t 26 min e 10 s.
Resposta da questão 44:
[D]
V ωR
Δθ
4x2π
.R
x0,8 6,4m / s .
Δt
3
Resposta da questão 45:
[D]
Em todo o movimento, a aceleração é g .
Na subida v é para cima, na descida, para baixo e no ponto mais alto v 0 .












