Determinação da massa do quark top Introdução A famosa equação

Determinação da massa do quark top
Introdução
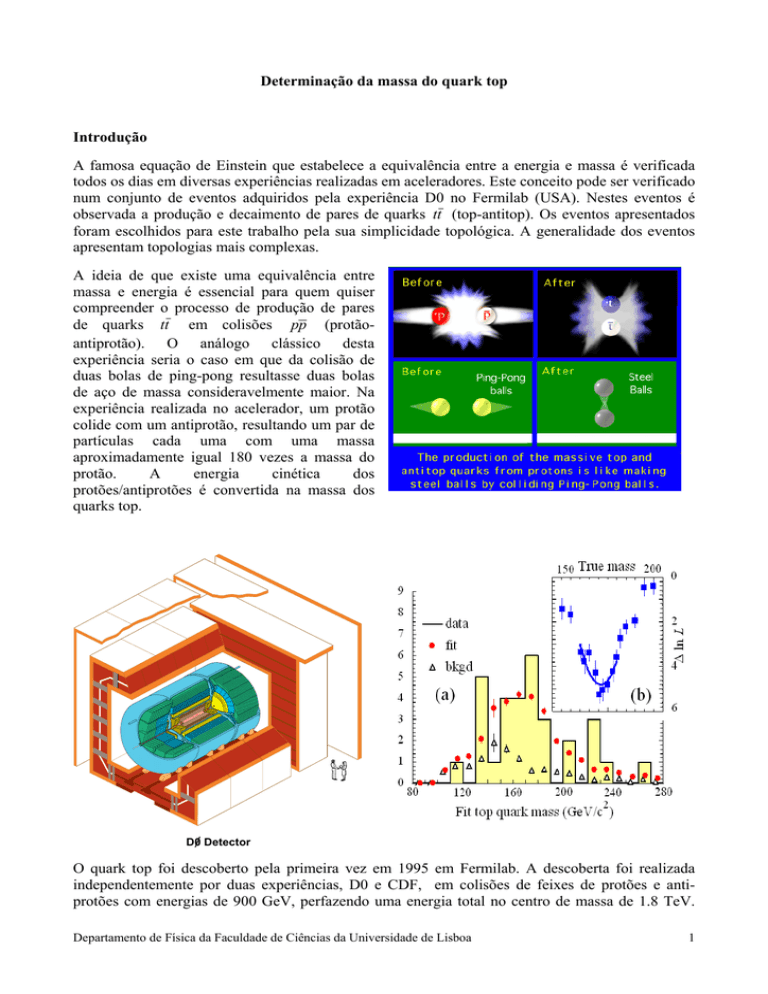
A famosa equação de Einstein que estabelece a equivalência entre a energia e massa é verificada
todos os dias em diversas experiências realizadas em aceleradores. Este conceito pode ser verificado
num conjunto de eventos adquiridos pela experiência D0 no Fermilab (USA). Nestes eventos é
observada a produção e decaimento de pares de quarks tt (top-antitop). Os eventos apresentados
foram escolhidos para este trabalho pela sua simplicidade topológica. A generalidade dos eventos
apresentam topologias mais complexas.
A ideia de que existe uma equivalência entre
massa e energia é essencial para quem quiser
compreender o processo de produção de pares
de quarks tt em colisões pp (protãoantiprotão). O análogo clássico desta
experiência seria o caso em que da colisão de
duas bolas de ping-pong resultasse duas bolas
de aço de massa consideravelmente maior. Na
experiência realizada no acelerador, um protão
colide com um antiprotão, resultando um par de
partículas cada uma com uma massa
aproximadamente igual 180 vezes a massa do
protão.
A
energia
cinética
dos
protões/antiprotões é convertida na massa dos
quarks top.
D0 Detector
O quark top foi descoberto pela primeira vez em 1995 em Fermilab. A descoberta foi realizada
independentemente por duas experiências, D0 e CDF, em colisões de feixes de protões e antiprotões com energias de 900 GeV, perfazendo uma energia total no centro de massa de 1.8 TeV.
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
1
Esta energia será partilhada entre a massa e energia cinética das partículas resultantes da colisão. Na
figura abaixo encontra-se uma representação que esquematiza uma colisão pp seguida de produção
e decaimento de um par tt .
Esquema da colisão pp .
Partículas detectadas em D0.
Esta é de facto uma de entre muitas possibilidades. O quark top é uma partícula de vida média
extremamente curta (da ordem de 4×10-25 s), que se desintegra dando origem a um quark b e a um
bosão W (mediador da interacção fraca). As partículas que resultam desta desintegração são também
elas instáveis, desintegrando-se em voo. Assim obtemos a cadeia de desintegrações que está
representada abaixo
t
b + W
lν ou jj
q + W
lν ou jj
j
em que q é um quark u ou c, j um jacto de partículas e o leptão l pode ser um electrão e, muão µ ou
tau τ. Um jacto é um conjunto de partículas, que aparecem segundo um cone e que resultam da
hadronização de um quark. Uma vez que nunca se observaram quarks isolados a hadronização é o
processo pelo o qual um quark após ter sido criado se agrupa com outros quarks para dar origem às
partículas detectadas. Nos eventos que irão ser estudados o bosão W resultante da desintegração do
quark b desintegra-se dando origem a um muão e a um neutrino. Este muão que aparece incluído no
jacto, possui uma energia pequena e ajuda a identificar a presença do quark b no evento. Por outro
lado consideram-se eventos em que o bosão W resultante da desintegração do top se desintegra em
dois jactos de partículas. Esta é a situação esquematizada na figura acima.
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
2
Energia, Massa e Momento
Para o cálculo da massa do quark top é essencial compreender-se o processo da determinação do
“momento em falta” do neutrino. Uma vez conhecido este momento teremos todos os ingredientes
necessários para o cálculo da massa do top.
A relação relativista para a energia total E de uma partícula livre estabelece que
E 2 = p 2c 2 + m 2c 4
em que p é o momento linear, c a velocidade da luz e m a massa da partícula. Neste domínio da
física é útil usar-se o sistema de unidades em que as energias são expressas em GeV, o momento em
GeV/c e a massa em GeV/c2. Este sistema de unidades é na prática equivalente ao sistema “natural”
de unidades onde se faz c=1. As equações vêm então simplificadas pelo facto do factor c
“desaparecer” das mesmas. A equação acima ficará então, E 2 = p 2 + m 2 ficando reforçada a
equivalência entre massa e energia. Define-se então massa invariante M de um sistema de n
partículas a partir da equação
M =
(∑ E ) − (∑ pr )
2
2
i
i
.
Esta quantidade é um invariante de Lorentz (não depende do referencial de inércia em que é
calculado) e é conservada na colisão. No caso da colisão de dois feixes de partículas de igual massa
r
r
m e energia E e que fazem entre si um ângulo de 180º, têm-se que p1 = − p2 pelo que o termo
r
2
∑ pi é nulo será nulo nesse caso. Ficamos então com M = (2 E ) = 2 E e portanto, se na colisão
produzirmos duas partículas em repouso e de massa m' igual teremos m' = E . Este é por exemplo o
caso em que a colisão é entre partículas elementares como um electrão e um positrão. Para produzir
um par partícula-antipartícula em repouso basta nesse caso “sintonizar” a energia do feixe para o
valor da massa da partícula a produzir. As colisões estudas em Fermilab foram contudo entre
protões e antiprotões. Estas partículas apresentam estrutura interna, sendo cada uma delas
constituída por três quarks (antiquarks). A colisão faz-se então entre um dos quarks do protão e um
dos antiquarks do antiprotão, não sendo necessário que a sua energia seja igual, pelo que o termo
r
∑ pi não será em geral nulo. No entanto, e uma vez que os feixes encontram-se alinhados entre si,
o momento linear só tem componente segundo a linha de feixe, pelo que o momento linear no plano
perpendicular à direcção do feixe é sempre nulo. No caso de eventos planares (eventos que se
encontram na prática contidos no plano perpendicular à linha de feixe) o momento linear segundo a
linha de feixe é também nulo (ou quase). Nestas condições é possível usar a expressão
M = 2mtop =
(∑ E )
2
i
para obtermos a massa do top a partir do valor das energias dos produtos da
colisão, uma vez que sendo o momento total conservado, esse valor é o mesmo antes e depois da
colisão. Embora os eventos planares não sejam os mais frequentes, existem alguns exemplos, onde
esta técnica pode ser utilizada.
No entanto um problema ainda fica por resolver. Do decaimento do W directamente descendente do
quark top resulta um neutrino muito energético que escapa à detecção. Assim a soma das energias
detectadas não perfaz 2mtop . Para avaliarmos a energia transportada pelo neutrino teremos que
recorrer à conservação do momento linear. Como foi explicado, a soma das componentes dos
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
3
momentos lineares no plano perpendicular deve resultar nula. A soma de todos os momentos
r
r
lineares visíveis pvis deverá ser simétrica ao momento do neutrino pυ que se escapa (momento “em
falta”)
n −1
r
r
r
p vis = ∑ pi = − pυ .
i =1
Por sua vez, como o neutrino tem uma massa desprezável tem-se que Eυ = pυ , pelo que se obtêm o
termo de energia que faltava para poder-se calcular a massa do quark top.
Procedimento Experimental
São fornecidos quatro eventos. Três deles são simulados em computador e um, o evento Run
92704 Event 14022, é real. Na figura abaixo estão duas projecções deste evento. Uma segundo o
plano perpendicular ao feixe, e outra, num plano que contem o feixe. Pode verificar-se que este
evento cumpre de forma aproximada o requisito de ser planar. Neste evento são visíveis jactos de
partículas, que resultam da hadronização quarks. Nos detectores, os jactos podem ser vistos como
conjuntos de deposições de energia nos detectores (as “torres” nas figuras).
Os eventos que vão ser estudados encontram-se segundo um corte transversal do detector. Os
detectores de altas energias são frequentemente constituídos por várias camadas de sub-dectores que
desempenham diferentes funções (ver figura abaixo).
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
4
Determinação da massa do top
Para cada evento determine o "momento em falta" através da soma de todos os momentos visíveis,
não esquecendo que o momento é uma grandeza vectorial! Nos gráficos, a torre magenta já indica a
direcção provável tomada pelo neutrino. Uma vez obtido o momento linear do neutrino, determine a
soma de todos os momentos (ou energias já que as massas envolvidas são pequenas) e obtenha a
massa do quark top dividindo esse valor por dois.
Momento (GeV/c)
Evento
Jacto1
Jacto 2
Jacto3
Jacto4
Muão
Duro
Muão
Suave
Neutrino Massa
Top
(GeV/c2)
Referências:
Tony M. Liss and Paul L. Tipton, Scientific American, Setembro 1997
B.R.Martin & G.Shaw, "Particle Physics", Wiley 1997
http://www-ed.fnal.gov
Departamento de Física da Faculdade de Ciências da Universidade de Lisboa
5