lista_va1_1ano_resolvida

Professora FLORENCE
1. Um ponto material desloca-se sobre uma reta e sua velocidade em função do tempo é
dada pelo gráfico. Pedem-se:
a) a equação horária da velocidade (função de v = f(t))
v(m/s)
b) o deslocamento do ponto material entre os instantes 0 e 2 s.
c) a velocidade escalar média entre 0 e 2 s.
d) a classificação do movimento em acelerado ou retardado.
9
Resposta:
a) v = 5 + 2t
b) 14 m
c) v = 7 m/s
d) acelerado
5
0
2
Resolução:
a) v = f(t)
A velocidade inicial é determinada quando t = 0, portanto v 0 = 5 m/s.
A aceleração pode ser calculada pelo gráfico através da tangente do ângulo α.
a = tg α  a = Δv/Δt  a = (v – v0)/(t - t0)
a = (9 – 5)/(2 – 0)  a = 4/2  a = 2 m/s2
Assim a função horária da velocidade fica:
v = v0 + at  v = 5 + 2t
b) Em um gráfico de v x t podemos calcular o deslocamento pela área do gráfico
abaixo da curva.
Este gráfico forma uma área que é um trapézio, assim temos:
Área  S 
(BaseMaior  basemenor ).altura
2
Área  S 
(9  5).2
2
c) v 
 ΔS = 14 m
S
14
 v
 v = 7 m/s
t
2
d) Como a aceleração é positiva a = 2 m/s2 e v > 0 durante todo o movimento, temos:
a>0
v>0
movimento
acelerado
Página 1 de 12
t(s)
Professora FLORENCE
2. O gráfico representa a velocidade de dois carros A e B que percorrem uma trajetória
retilínea.
a) Os carros A e B realizam um movimento uniformemente variado? Justifique sua
resposta
v
b) Qual dos carros tem maior aceleração? Por quê?
A
B
t
0
Resolução:
a) sim, ambos apresentam a velocidade variando linearmente com o tempo.
b) O carro A está mais acelerado, a reta que indica a velocidade tem maior inclinação
que a reta que indica a velocidade do carro B.
3. As funções horárias das velocidades de dois corpos em movimento são vA = 4t e vB =
30 – 5t (no SI). Construa, num mesmo sistema de dois eixos, os gráficos dessas funções.
Resolução:
Para construir o gráfico do movimento dos dois carros deve-se fazer a tabela abaixo
usando as funções dos carros.
Assim:
v(m/s)
t(s)
vA= 0 + 4t
VB =30 – 5t
0
0
30
1
4
25
2
8
20
3
12
15
4
16
10
30
20
A
10
B
t(s)
0
1
2
3
4
Página 2 de 12
Professora FLORENCE
4. (Unicamp – SP) A tabela mostra os valores da velocidade de um atleta da São
Silvestre em função do tempo, nos segundos iniciais da corrida.
t(s)
0,0
v(m/s) 0,0
1,0
1,8
2,0
3,6
3,0
5,4
4,0
7,2
5,0
9,0
a) Esboce o gráfico da velocidade do atleta em função do tempo.
b) Calcule a aceleração do atleta nos primeiros 5 s da corrida.
Resposta:
a) fazer gráfico de v x t
b) 1,8 m/s
Resolução:
a) Da tabela retiramos os dados para o gráfico. Três pontos é o suficiente para
esboçar um gráfico.
v(m/s)
9
5,4
1,8
α
t(s)
0
1
3
5
b) O cálculo da aceleração pode ser feito pelo gráfico, através da tangente do ângulo
α. Também pode ser realizado utilizando os dados da tabela.
tg 
v
v
90
 tg  tg 
 a
 a = 1,8 m/s2
t
t
50
6. (Fuvest – SP) Um trem de metrô parte de uma estação com aceleração uniforme até
atingir, após 10 s, a velocidade escalar de 90 km/h, que é mantida durante 30 s para
então desacelerar uniformemente durante 10 s até parar na estação seguinte.
a) Represente graficamente a velocidade escalar em função do tempo.
b) Calcule a distância entre as duas estações.
Resposta:
a) fazer gráfico
b) 1,0 km/h
Página 3 de 12
Professora FLORENCE
Resolução:
a) Na primeira parte o trem vai aumentando a velocidade até atingir a velocidade de 90
km/h = 25 m/s, para isso ele leva o tempo de 10 s.
90km / h
 25m / s
3,6
Após isso, o trem mantém a velocidade de 25 m/s durante 30 s, portanto a velocidade
é constante entre os tempos 40 s e 10 s (40 – 10 = 30 s).
Depois ocorre a desaceleração em 10 s, portanto tempo total do percurso 50 s, até
que a velocidade atinja o valor 0.
v(m/s)
25
t(s)
0
10
40
50
b) Em um gráfico de v x t podemos calcular a distância através da área do gráfico
abaixo da curva.
Este gráfico forma uma área que é um trapézio, assim temos:
Área  S 
(BaseMaior  basemenor ).altura
2
Área  S 
(50  30).25
2
 ΔS = 1000 m  ΔS = 1 km
7. (FUFPI) O gráfico abaixo representa a velocidade escalar, em função do tempo, para
o movimento de um corpo que se desloca em linha reta.
a) Qual a aceleração escalar no instante t = 5,0 s?
b) Em que instante a velocidade escalar vale 8,0 m/s?
Página 4 de 12
Professora FLORENCE
v(m/s)
Resposta:
a) 4 m/s
b) 3s
20
6
0
t(s)
5
-4
Resolução:
a) O cálculo da aceleração pode ser feito pelo gráfico, através da tangente do ângulo
α.
tg 
v
v
0  20
 a
 a = – 4 m/s2
 tg  tg 
t
t
50
Obs: deveríamos esperar uma aceleração negativa, pois a reta do gráfico é
decrescente e sua inclinação já nos mostrava esse fato.
b) para determinarmos a velocidade de um móvel em qualquer tempo, escrevemos
sua equação horária v = v0 + at. Para esse movimento temos a seguinte equação:
v0 = 20 m/s  a aceleração foi calculada no item acima a= – 4 m/s2  v = 20 – 4t.
Para determinar o tempo quando a velocidade for igual a 8 m/s, fazemos:
v = 20 – 4t  8 = 20 – 4t  8 – 20 = – 4t  – 12 = – 4t  t 
 12
t=3s
4
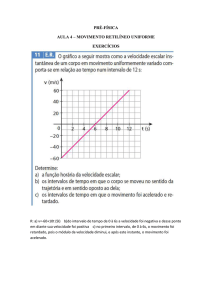
7. A velocidade escalar de um móvel sobre uma trajetória retilínea varia com o tempo
de acordo com o gráfico.
a) Qual a distância percorrida pelo móvel no intervalo de 0 a 20 s?
b) Qual a velocidade escalar média de 0 a 20 s?
c) Em quais intervalos de tempo o movimento é acelerado?
v(m/s)
10
12
0
4
8
16
20
t(s)
-10
Página 5 de 12
Professora FLORENCE
Resposta:
a) 120 m
b) 6 m/s
c) 0 a 4 s e entre 16 e 20 s
Resolução:
a) Em um gráfico de v x t a distância percorrida é calculada pela área do gráfico abaixo
da curva. Para esse gráfico temos duas áreas para calcular, área do triângulo e a área
do trapézio. Após o cálculo somaremos as áreas:
Áreas  D 
Cálculo da área do triângulo:
Área  d1 
(Base. Altura )

2
Área  d1 
(10.8)
 d1 = 40 m
2
Cálculo da área do trapézio:
Área  d 2 
(BaseMaior  basemenor ).altura
2
Área  d 2 
(12  4).(10)
2
 |d2| = 80 m
Distância total = d1 + |d2| = 40 + 80  D = 120 m
b) Para determinar a velocidade utilizamos a distância calculada no item acima e o
tempo total que o móvel levou para percorrê-la, pelo gráfico o tempo é de 20 s.
v
S
120
 v
 v = 6 m/s
t
20
c) Pelo gráfico observamos que o movimento é acelerado de 0 a 4 s e entre 16 s a 20
s.
8. (IFSC 2011) De acordo com o texto, 4 quilômetros é a distância do chão até a altura
do avião. Se um objeto pequeno for solto dessa altura, quanto tempo em segundos
levaria para chegar ao solo? (Despreze a resistência do ar e considere a aceleração
gravitacional do local de 10m / s2 ).
a) 800 s .
b) 2065 s
c) 2865 s
d) 4443 s
e) 9998 s
Resposta:
Página 6 de 12
Professora FLORENCE
[A]
Dados: h = 4 km = 4.000 m; g = 10 m/s2.
Da equação da queda livre:
h
1 2
gt
2
 t
2h

g
2  4.000 
10
 t  800 s.
9. (Fuvest 2010) Na Cidade Universitária (USP), um jovem, em um carrinho de rolimã,
desce a rua do Matão, cujo perfil está representado na figura a seguir, em um sistema de
coordenadas em que o eixo Ox tem a direção horizontal.
No instante t = 0, o carrinho passa em movimento pela posição y = y0 e x = 0.
Dentre os gráficos das figuras a seguir, os que melhor poderiam descrever a posição x e
a velocidade v do carrinho em função do tempo t são, respectivamente,
a) I e II.
b) I e III.
c) II e IV.
d) III e II.
e) IV e III.
Resposta:
[A]
Página 7 de 12
Professora FLORENCE
A situação proposta sugere que consideremos, no início, movimento acelerado e, a
seguir, movimento uniforme. Por isso os gráficos I e II são os que melhor representam
as variações espaço  tempo e velocidade  tempo, respectivamente.
10. (CFTMG 2010) O gráfico da velocidade em função do tempo representa o
movimento de uma partícula.
Esse movimento pode ser classificado como ____________ no intervalo de tempo
compreendido entre __________.
A opção que completa, corretamente, as lacunas acima é
a) acelerado, zero e 1 h.
b) acelerado, zero e 2 h.
c) desacelerado, zero e 1 h.
d) desacelerado, 1 h e 2 h.
Resposta:
[C]
No intervalo de 0 a 1 h, a velocidade escalar é positiva e tem módulo decrescente.
Então, o movimento é progressivo e desacelerado.
No intervalo de 1 h a 2 h, a velocidade escalar é negativa e tem módulo crescente.
Então, o movimento é regressivo (ou retrógrado) e acelerado.
11. (Enem 2ª aplicação 2010) Rua da Passagem
Os automóveis atrapalham o trânsito.
Gentileza é fundamental.
Não adianta esquentar a cabeça.
Menos peso do pé no pedal.
O trecho da música, de Lenine e Arnaldo Antunes (1999), ilustra a preocupação com o
trânsito nas cidades, motivo de uma campanha publicitária de uma seguradora
brasileira. Considere dois automóveis, A e B, respectivamente conduzidos por um
motorista imprudente e por um motorista consciente e adepto da campanha citada.
Ambos se encontram lado a lado no instante inicial t = 0 s, quando avistam um
semáforo amarelo (que indica atenção, parada obrigatória ao se tornar vermelho). O
Página 8 de 12
Professora FLORENCE
movimento de A e B pode ser analisado por meio do gráfico, que representa a
velocidade de cada automóvel em função do tempo.
As velocidades dos veículos variam com o tempo em dois intervalos: (I) entre os
instantes 10s e 20s; (II) entre os instantes 30s e 40s. De acordo com o gráfico, quais são
os módulos das taxas de variação da velocidade do veículo conduzido pelo motorista
imprudente, em m/s2, nos intervalos (I) e (II), respectivamente?
a) 1,0 e 3,0
b) 2,0 e 1,0
c) 2,0 e 1,5
d) 2,0 e 3,0
e) 10,0 e 30,0
Resposta:
[D]
Pelo gráfico, percebe-se que o motorista imprudente é o condutor do veículo A, que
recebe acelerações e desacelerações mais bruscas.
De 10 s a 20 s: |a(I)| =
De 30 s a 40 s: a(II) =
30  10 20
 |a(I)| =

20  10 10
0  30
30

 a(II)
40  30
10
2,0 m/s2.
= 3,0 m/s2.
12. (Unemat 2010) Um corpo possui movimento retilíneo, com velocidade variando
no decorrer do tempo, conforme o gráfico abaixo.
Página 9 de 12
Professora FLORENCE
Assinale a alternativa correta.
a) A aceleração do corpo é nula no intervalo de tempo IV.
b) A aceleração do corpo é constante no intervalo de tempo IV.
c) A aceleração do corpo é nula no intervalo de tempo I.
d) A aceleração do corpo é maior no intervalo de tempo III do que no intervalo de
tempo I.
e) A aceleração do corpo é variável nos intervalos de tempo II e IV.
Resposta:
[B]
Como o movimento é retilíneo, a aceleração tem módulo igual ao módulo da aceleração
escalar, dado por:
| a |
| v |
.
t
Assim:
aI = aII (constante)  0; aIII = 0; aIV  0 (constante)
13. (Pucpr 2010) Um motociclista dirige uma motocicleta ao longo de uma estrada reta
como mostrado no diagrama velocidade x tempo.
A respeito dessa situação, assinale a alternativa correta:
a) Entre os instantes t = 3 s e t = 5 s o movimento é acelerado.
b) A aceleração no intervalo de tempo entre t = 5 s e t = 7 s vale – 4 m/s2.
c) O deslocamento do motociclista entre os instantes t = 3 s e t = 5 s foi de 20 m.
d) A aceleração no intervalo de tempo entre t = 5 s e t = 7 s vale 2 m/s 2 .
e) A aceleração no intervalo de tempo entre t = 0 e t = 3 s é nula.
Resposta:
[B]
Analisemos cada intervalo:
Página 10 de 12
Professora FLORENCE
– De 0 a 3 s: o movimento é uniformemente acelerado; a aceleração escalar é
a1 =
v1 8
2
  2,7 m/s .
t1 3
O espaço percorrido é calculado pela “área” de 0 a 3 s
S1 
38
 12 m.
2
– De 3 s a 5 s: o movimento é uniforme, com velocidade escalar v2 = 8 m/s.
O espaço percorrido é:
S2 = v2 t2  8  2 = 16 m.
– De 5 s s 7 s: o movimento é uniformemente retardado; a aceleração escalar é:
a3 =
v 3 0  8 8
2


 4 m/s .
t 3 7  5
2
O espaço percorrido é:
S3 
28
 8 m.
2
14. (Ufrgs 2010) Observe o gráfico a seguir, que mostra a velocidade instantânea V em
função do tempo t de um móvel que se desloca em uma trajetória retilínea. Neste
gráfico, I, II e III identificam, respectivamente, os intervalos de tempo de 0s a 4s, de 4s
a 6s e de 6s a 14s.
Nos intervalos de tempo indicados, as acelerações do móvel valem, em m/s2,
respectivamente,
a) 20, 40, e 20.
b) 10, 20 e 5.
c) 10, 0 e -5.
d) -10, 0 e 5.
e) -10, 0 e -5.
Resposta:
Página 11 de 12
Professora FLORENCE
[C]
Como a trajetória é retilínea, a aceleração restringe-se à componente tangencial ( a t ),
que, em módulo, é igual a aceleração escalar (a), dada pela taxa de variação da
velocidade (v) em relação ao tempo (t).
a=
v
t
I. aI =
. Usando essa expressão em cada um dos intervalos:
40  0
40
 aI = 10 m/s2.
II. aII = 0 (não houve variação da velocidade)
III. aIII =
0  40 40

14  6
8
 aIII = – 5 m/s2.
Página 12 de 12