Halliday Fundamentos de Física Volume 2

Halliday
Fundamentos de Física
Volume 2
www.grupogen.com.br
http://gen-io.grupogen.com.br
O GEN | Grupo Editorial Nacional reúne as editoras Guanabara Koogan, Santos, Roca, AC Farmacêutica,
LTC, Forense, Método, E.P.U. e Forense Universitária
O GEN-IO | GEN – Informação Online é o repositório de material suplementar dos livros dessas editoras
www.grupogen.com.br
http://gen-io.grupogen.com.br
Capítulo 12
Equilíbrio e Elasticidade
12.1 Física e Equilíbrio
• O que faz com que um objeto permaneça estável
na presença de forças?
• Em que condições os objetos se deformam?
12.2 Equilíbrio
As duas condições para o estado de equilíbrio são
as seguintes:
1. O momento linear do centro de massa deve ser
constante.
2. O momento angular em relação ao centro de
massa, ou em relação a qualquer outro ponto,
deve ser constante.
A pedra da Fig. 12-1 é um exemplo de um objeto
que está em equilíbrio estático. Nessa situação,
as duas condições acima são satisfeitas.
Figura 12-1 Uma pedra em equilíbrio.
Embora a sustentação pareça precária,
a pedra está em equilíbrio estático.
(Symon Lobsang/Photis/Jupiter
Images Corp.)
12.3 As Condições de Equilíbrio
Outro requisito para o equilíbrio estático:
12.4 O Centro de Gravidade
Exemplo: equilíbrio estático
Exemplo: equilíbrio estático
Exemplo: equilíbrio estático (cont.)
Exemplo: equilíbrio estático
12.6: Estruturas Indeterminadas
12.7: Elasticidade
A tensão é definida como a força por unidade de área que produz uma
deformação.
Tensão e deformação são proporcionais; a constante de
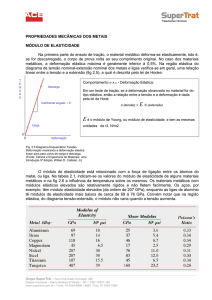
proporcionalidade é chamada de módulo de elasticidade.
12.7: Elasticidade: Tração e Compressão
No caso de uma tração ou compressão, a
tensão é definida como F/A, onde F é o
módulo de uma força aplicada
perpendicularmente a uma área A do objeto.
A deformação é a grandeza adimensional
∆L/L que mede a variação relativa do
comprimento do objeto.
No caso de uma tensão trativa ou
compressiva, o módulo de elasticidade é
chamado de módulo de Young e
representado pelo símbolo E.
12.7: Elasticidade: Cisalhamento
No caso do cisalhamento, a tensão também é uma força por unidade de área,
mas o vetor força está no plano da área e não na direção perpendicular a esse
plano. A deformação é a razão adimensional ∆x/L, onde ∆x e L são as
grandezas mostradas na figura. O módulo de elasticidade correspondente é
chamado de módulo de cisalhamento e representado pelo símbolo G.
12.7: Elasticidade: Tensão Hidrostática
Na figura, a tensão é a pressão p que o fluido exerce sobre o objeto, onde a
pressão é definida como força por unidade de área.
A deformação é ∆V/V, na qualV é o volume original do objeto e ∆V é o valor
absoluto da variação de volume.
O módulo de elasticidade correspondente é chamado de módulo de
elasticidade volumétrico e representado pelo símbolo B. Dizemos que o
objeto está sob compressão hidrostática e a pressão pode ser chamada de
tensão hidrostática.
12.7: Elasticidade
Exemplo: tensão e deformação de uma barra
Exemplo: mesa bamba
Tomamos a mesa e o cilindro de aço como nosso sistema. A
situação é a da figura, exceto pelo fato de que agora temos
um cilindro de aço sobre a mesa. Se o tampo da mesa
permanece nivelado, as pernas devem estar comprimidas da
seguinte forma: cada uma das pernas mais curtas sofreu o
mesmo encurtamento (vamos chamá-lo de ∆L3) e, portanto,
está submetida à mesma força F3. A perna mais comprida
sofreu um encurtamento maior, ∆L4 e, portanto, está
submetida a uma força F4 maior que F3.