Exemplos de seleção de fuso de esferas

510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
Exemplos de seleção de fuso de esferas
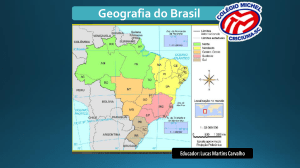
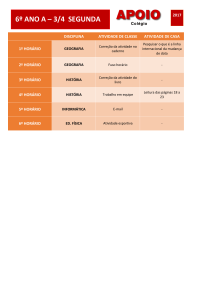
Equipamentos de transferência de alta velocidade (uso horizontal)
[Condições de seleção]
Massa da mesa
Massa de trabalho
Comprimento do curso
Velocidade máxima
Tempo de aceleração
Tempo de desaceleração
Número de recíprocas por minuto
Folga
Precisão no posicionamento
m1 = 60 kg
m2 = 20 kg
ℓS = 1000 mm
Vmax = 1 m/s
t1 = 0,15 s
t3 = 0,15 s
n = 8 min-1
0,15 mm
0,3 mm/1000 mm
(Faça o posicionamento
pela direção negativa)
Repetição de precisão no posicionamento 0,1 mm
Quantidade mínima de alimentação s = 0,02 mm/pulso
Vida útil de serviço desejada 30000 h
Motor propulsor
servomotor CA
Velocidade nominal de rotação:
3.000 min-1
Momento de inércia do motor Jm = 1×10‒3 kg•m2
Engrenagem de redução Nenhuma (acoplamento direto)A= 1
Coeficiente de atrito da superfície do guia  = 0,003 (rolamento)
Resistência da superfície do guia f = 15 N (sem carga)
Massa da peça
+
Massa da mesa
m2
+
m1
Eixo da gaiola
de esferas
Fuso de esferas
Motor
Castanha do
fuso de esferas
[Itens de seleção]
Diâmetro do eixo
Avanço
Modelo da castanha
Precisão
Folga axial
Método de suporte do eixo
Motor propulsor
B15-69
510BZ
[Seleção de precisão do ângulo de avanço e folga axial]
 Seleção de precisão do ângulo de avanço
Para obter precisão no posicionamento de 0,3 mm/1.000 mm:
±0,09
±0,3
=
1000
300
A precisão do ângulo de avanço deve ser 0,09 mm/300 mm ou maior.
Logo, selecione o grau de precisão a seguir para o fuso de esferas (consultar a Tabela1 na página
B15-20).
C7 (erro de distância percorrida: 0,05 mm/300 mm)
O grau de precisão C7 está disponível para ambos os fusos de esfera laminados e os de precisão.
Suponha que um fuso de esferas laminado foi selecionado para essa situação devido ao seu menor
custo.
 Seleção da folga axial
Para satisfazer a folga de 0,15 mm, é necessário selecionar um fuso de esferas com folga axial de
0,15 mm ou menor.
Portanto, um modelo de fuso de esferas laminado com eixo de 32 mm de diâmetro ou menor atende
ao requisito de folga axial de 0,15 mm ou menor (consulte a Tabela13 na página B15-27).
Portanto, um modelo de fuso de esferas laminado com eixo de 32 mm de diâmetro ou menor e grau
C7 de precisão é selecionado.
[Seleção de um eixo]
 Suposição do comprimento do eixo
Suponha que o comprimento total da castanha seja 100 mm e o comprimento da ponta do eixo seja
100 mm.
Portanto, o comprimento total é determinado pelo modelo a seguir, baseado no comprimento de
curso de 1.000 mm.
1000 + 200 = 1200 mm
Portanto, o comprimento do eixo será de 1.200 mm.
 Seleção de um avanço
Com a velocidade nominal de rotação do motor propulsor sendo 3.000 min-1 e a velocidade máxima
sendo 1 m/s, o avanço do fuso de esferas é obtido da maneira a seguir:
1×1000×60
3000
= 20 mm
Portanto, é necessário selecionar um tipo com avanço de 20 mm ou maior.
Além disso, o fuso de esferas e o motor podem ser montados em acoplamento direito, utilizando
uma engrenagem de redução. A resolução mínima por rotação de um servomotor CA é obtida baseada na revolução do codificador (1.000 p/rev; 1.500 p/rev) fornecido como acessório padrão para o
servomotor CA, conforme indicado abaixo.
1000 p/rev (sem multiplicação)
1500 p/rev (sem multiplicação)
2000 p/rev (dobrado)
3000 p/rev (dobrado)
4000 p/rev (quadruplicado)
6000 p/rev (quadruplicado)
B15-70
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
Para cumprir a quantidade mínima de alimentação de 0,02 mm/pulso, que é o requisito de seleção,
os dados abaixo devem ser aplicados.
Avanço
20 mm —— 1000 p/rev
30 mm —— 1500 p/rev
40 mm —— 2000 p/rev
60 mm —— 3000 p/rev
80 mm —— 4000 p/rev
 Seleção do diâmetro do eixo
 Seleção de um método de suporte de eixo
Como o tipo pressuposto possui um comprimento de curso longo de 1.000 mm e opera na alta velocidade de 1 m/s, selecione a configuração fixo-apoiado ou fixo-fixo para o suporte do eixo.
No entanto, a configuração fixo-fixo requer uma estrutura complicada, e necessita de alta precisão
na instalação.
Consequentemente, a configuração fixo-apoiada é selecionada com método de apoio do eixo.
B15-71
Fuso de esferas
Os modelos de fuso de esferas que atendem aos requisitos definidos na seção [Seleção de precisão do ângulo de avanço e folga axial] na página B15-70: um fuso de esferas laminado com
eixo de 32 mm de diâmetro ou menor; e o requisito definido na seção [Seleção de um eixo] na página B15-70: um avanço de 20, 30, 40, 60 ou 80 mm (consulte a Tabela20 na página B1535) são os determinados a seguir.
Diâmetro do eixo Avanço
15 mm —— 20 mm
15 mm —— 30 mm
20 mm —— 20 mm
20 mm —— 40 mm
30 mm —— 60 mm
Como o comprimento do eixo deve ser 1.200 mm, como indicado na seção [Seleção de um eixo]
na página B15-70, o diâmetro de 15 mm do eixo é insuficiente. Portanto, o fuso de esferas
deve possuir um eixo com diâmetro de 20 mm ou maior.
Consequentemente, existem três combinações de diâmetros de eixo e avanços que atendem aos
requisitos: eixo com diâmetro de 20 mm/avanço de 20 mm; 20 mm/40 mm; e 30 mm/60 mm.
510BZ
 Estudo da carga axial permitida
Cálculo da carga axial máxima
Resistência da superfície do guia
f = 15 N (sem carga)
Massa da mesa
m1 = 60 kg
Massa de trabalho
m2 = 20 kg
Coeficiente de atrito da superfície do guia
 = 0,003
Velocidade máxima
Vmax = 1 m/s
Aceleração gravitacional
g = 9,807 m/s2
Tempo de aceleração
t1 = 0,15 s
Consequentemente, os valores requisitados são obtidos da maneira a seguir.
Aceleração:
α=
Vmax
= 6,67 m/s2
t1
Durante a aceleração de avanço:
Fa1 = • (m1 + m2) g + f + (m1 + m2) • = 550 N
Durante movimento uniforme de avanço:
Fa2 = • (m1 + m2) g + f = 17 N
Durante a desaceleração de avanço:
Fa3 = • (m1 + m2) g + f ‒ (m1 + m2) • = ‒516 N
Durante a aceleração regressiva:
Fa4 = ‒• (m1 + m2) g ‒ f ‒ (m1 + m2) • = ‒550 N
Durante movimento regressivo uniforme:
Fa5 = ‒• (m1 + m2) g ‒ f = ‒ 17 N
Durante a desaceleração regressiva:
Fa6 = ‒• (m1 + m2) g ‒ f + (m1 + m2) • = 516 N
Portanto, a carga axial máxima aplicada no fuso de esferas é a seguinte:
Famax = Fa1 = 550 N
Portanto, se não há problema com o diâmetro de 20 mm do eixo e um avanço de 20 mm (menor
diâmetro menor da rosca de 17,5 mm), então o diâmetro de 30 mm do eixo atende aos requisitos.
Consequentemente, os cálculos a seguir para a carga de flambagem e a carga de compressão e
tensão permitidas do eixo são executados ao supormos que o diâmetro do eixo seja 20 mm e o
avanço, 20 mm.
B15-72
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
Carga de flambagem no eixo
Fator de acordo com o método de montagem
Supondo que o método de montagem da seção entre
gem deve ser considerada, é “fixo-fixo: “
Distância entre as duas superfícies de montagem
Diâmetro menor da rosca do eixo
2=20 (consulte B15-38)
a castanha e o mancal, onde a flambaℓa=1100 mm (estimativa)
d1=17,5 mm
4
P1 = η2 •
4
d1
4
4
17,5
2 ×10 = 20×
2 × 10 = 15500 N
ℓa
1100
Carga de compressão e tensão permitidas do eixo
P2 = 116 × d12 = 116 × 17,52 = 35500 N
Portanto, a carga de flambagem e a carga de compressão e tensão permitidas do eixo são, ao
menos, iguais à carga axial máxima. Consequentemente, um fuso de esferas que atenda a esses
requisitos pode ser utilizado sem problemas.
 Estudo da velocidade de rotação permitida
Velocidade máxima de rotação
● Diâmetro do eixo: 20 mm; avanço: 20 mm
Velocidade máxima Vmax= 1 m/s
Avanço
Ph= 20 mm
Fuso de esferas
3
Nmax =
Vmax × 60×10
–1
= 3000 min
Ph
● Diâmetro do eixo: 20 mm; avanço: 40mm
Velocidade máxima Vmax= 1 m/s
Avanço
Ph= 40 mm
3
Nmax =
Vmax × 60×10
–1
= 1500 min
Ph
● Diâmetro do eixo: 30 mm; avanço: 60 mm
Velocidade máxima Vmax= 1 m/s
Avanço
Ph= 60 mm
3
Nmax =
Vmax × 60×10
–1
= 1000 min
Ph
B15-73
510BZ
Velocidade de rotação permitida determinada pela velocidade perigosa do eixo
Fator de acordo com o método de montagem
2=15,1 (consulte B15-40)
Supondo que o método de montagem para a seção entre a castanha e o mancal, onde a velocidade perigosa deve ser considerada, é “fixo-fixo: “
ℓb=1100 mm (estimativa)
Distância entre duas superfícies de montagem
● Diâmetro do eixo: 20 mm; avanço: 20 mm e 40 mm
Diâmetro menor da rosca do eixo
d1=17,5mm
N1 = λ2×
d1
7
7
–1
17,5
2 × 10 = 2180 min
2 10 = 15,1×
1100
ℓb
● Diâmetro do eixo: 30 mm; avanço: 60 mm
Diâmetro menor da rosca do eixo
N1 = λ2×
d1= 26,4mm
d1
7
7
–1
26,4
10 = 15,1×
2 × 10 = 3294 min
2
1100
ℓb
Velocidade de rotação permitida determinada pelo Valor DN
● Diâmetro do eixo: 20 mm; avanço: 20 mm e 40 mm (fuso de esferas de avanço amplo)
Diâmetro da esfera de centro a centro
D= 20,75 mm
N2 =
–1
70000
70000
=
= 3370 min
D
20,75
● Diâmetro do eixo: 30 mm; avanço: 60 mm (fuso de esferas de avanço amplo)
Diâmetro da esfera de centro a centro
D= 31,25 mm
N2 =
–1
70000
70000
=
= 2240 min
D
31,25
Portanto, com um fuso de esferas que possua um eixo com diâmetro de 20 mm e avanço de
20 mm, a velocidade de rotação máxima excede a velocidade perigosa.
No entanto, uma combinação de eixo de 20 mm de diâmetro e avanço de 40 mm, ou uma de eixo
de 30 mm de diâmetro e avanço de 60 mm, cumpre o requisito de velocidade perigosa e o valor
DN.
Consequentemente, um fuso de esferas com eixo de 20 mm de diâmetro e avanço de 40 mm, ou
um eixo com 30 mm de diâmetro e avanço de 60 mm, é selecionado.
[Seleção de castanha]
 Seleção de um modelo de castanha
Modelos de fuso de esferas laminado com eixo com diâmetro de 20 mm e avanço de 40 mm, ou
um eixo com diâmetro de 30 mm e avanço de 60 mm, são variações de modelos WTF de fuso de
esferas laminado de avanço amplo.
WTF2040-2
(Ca=5,4 kN, C0a= 13,6 kN)
WTF2040-3
(Ca=6,6 kN, C0a= 17,2 kN)
WTF3060-2
(Ca=11,8 kN, C0a= 30,6 kN)
WTF3060-3
(Ca=14,5 kN, C0a= 38,9 kN)
B15-74
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
 Estudo da carga axial permitida
Estudo da carga axial permitida do modelo WTF2040-2 (C0a = 13,6 kN).
Supondo que o modelo é utilizado em equipamentos de transferência de alta velocidade e que
uma carga de impacto é aplicada durante a desaceleração, defina o fator de segurança estática (fS)
como 2,5 (consulte Tabela1 na página B15-47).
C 0a
13,6
=
= 5,44 kN = 5440 N
fS
2,5
A carga axial permitida obtida é maior que a carga axial máxima de 550 N. Portanto, não ocorrerão
problemas com esse modelo.
Cálculo da distância percorrida
Velocidade máxima
Vmax= 1 m/s
Tempo de aceleração
t1 = 0,15 s
Tempo de desaceleração t3 = 0,15 s
● Distância percorrida durante a aceleração
ℓ1, 4 =
Vmax • t1
1 × 0,15
×103 = 75 mm
× 103 =
2
2
● Distância percorrida durante o movimento uniforme
Vmax • t1 + Vmax • t3
1 × 0,15 + 1×0,15
×103 = 850 mm
× 103 = 1000 –
2
2
● Distância percorrida durante a desaceleração
ℓ3, 6 =
Vmax • t3
1 × 0,15
× 103 = 75 mm
×103 =
2
2
Com base nas condições acima, a relação entre a carga axial aplicada e a distância percorrida é
mostrada na tabela abaixo.
Movimento
Carga axial aplicada Distância percorrida
ℓN(mm)
FaN(N)
N° 1: durante a aceleração
de avanço
550
75
N° 2: durante o movimento
uniforme de avanço
17
850
N° 3: durante a desaceleração de avanço
‒516
75
N° 4: durante a aceleração
regressiva
‒550
75
N° 5: durante o movimento
regressivo uniforme
‒17
850
N° 6: durante a desaceleração regressiva
516
75
＊ O subscrito (N) indica um número de movimentos.
Como a direção da carga (expressa com um sinal de positivo ou negativo) é revertida com Fa3, Fa4
e Fa5, calcule a carga axial média em ambas as direções.
B15-75
Fuso de esferas
ℓ2, 5 = ℓS –
510BZ
Carga axial média
● Carga axial média na direção positiva
Como ocorre variação na direção da carga, calcule a carga axial média supondo que Fa3, 4, 5 = 0N.
3
Fm1 =
Fa1 × ℓ1 + Fa2 × ℓ2 + Fa6 × ℓ6
= 225 N
ℓ1 + ℓ2 + ℓ3 + ℓ4 + ℓ5 + ℓ6
3
3
3
● Carga axial média na direção negativa
Como ocorre variação na direção da carga, calcule a carga axial média supondo que Fa1, 2, 6 = 0N.
3
Fa3 × ℓ3 + Fa4 × ℓ4 + Fa5 × ℓ5 = 225 N
ℓ1 + ℓ2 + ℓ3 + ℓ4 + ℓ5 + ℓ6
3
Fm2 =
3
3
Como Fm1 = Fm2, suponha que a carga axial média seja Fm = Fm1 = Fm2 = 225 N.
Vida nominal
Fator de carga
Carga média
Vida nominal
fW= 1,5 (consulte Tabela2 na página B15-48)
Fm= 225 N
L (rev)
3
L=
( f CaF ) × 10
w·
6
m
Número pressuposto do
modelo
Capacidade de carga
nominal
Ca(N)
Vida nominal
L(rev)
WTF 2040-2
5400
4,1×109
WTF 2040-3
6600
7,47×109
WTF 3060-2
11800
4,27×1010
WTF 3060-3
14500
7,93×1010
B15-76
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
Média de revoluções por minuto
Número de recíprocas por minuto
Curso
● Avanço: Ph= 40 mm
Nm =
n = 8 min-1
ℓS= 1000 mm
2 ×n ×ℓs
2 × 8 × 1000
=
= 400 min–1
40
Ph
● Avanço: Ph= 60 mm
Nm =
2 ×n ×ℓs
2 × 8 × 1000
=
= 267 min–1
60
Ph
Calculando a vida útil de serviço com base na vida nominal
● WTF2040-2
Vida nominal
L=4,1×109 rev
Média de revoluções por minuto
Nm = 400 min-1
Lh =
L
=
60× Nm
4,1× 109
60× 400
Lh =
L
7,47×109
=
= 311000 h
60× 400
60× Nm
● WTF3060-2
Vida nominal
Média de revoluções por minuto
Lh =
L=4,27×1010 rev
Nm = 267 min-1
L
4,27×1010
=
= 2670000 h
60× 267
60× Nm
● WTF3060-3
Vida nominal
Média de revoluções por minuto
Lh =
L=7,47×109 rev
Nm = 400 min-1
Fuso de esferas
● WTF2040-3
Vida nominal
Média de revoluções por minuto
= 171000 h
L=7,93×1010 rev
Nm = 267 min-1
L
7,93×1010
=
= 4950000 h
60× 267
60× Nm
B15-77
510BZ
Calculando a vida útil de serviço na distância percorrida com base na vida nominal
● WTF2040-2
Vida nominal
L=4,1×109 rev
Avanço
Ph= 40 mm
LS = L × Ph× 10-6 = 164000 km
● WTF2040-3
Vida nominal
L=7,47×109 rev
Avanço
Ph= 40 mm
LS = L × Ph× 10-6 = 298800 km
● WTF3060-2
Vida nominal
L=4,27×1010 rev
Avanço
Ph= 60 mm
LS = L × Ph× 10-6 = 2562000 km
● WTF3060-3
Vida nominal
L=7,93×1010 rev
Avanço
Ph= 60 mm
LS = L × Ph× 10-6 = 4758000 km
De acordo com todas as condições descritas acima, os modelos a seguir satisfazem o tempo de
vida útil desejado de 30.000 horas e são selecionados.
WTF 2040-2
WTF 2040-3
WTF 3060-2
WTF 3060-3
B15-78
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
[Estudo da rigidez]
Como as condições para seleção não incluem rigidez e esse elemento não é particularmente necessário, ele não será descrito aqui.
[Estudo da precisão no posicionamento]
 Estudo da precisão do ângulo de avanço
O grau de precisão C7 foi selecionado na seção [Seleção de precisão do ângulo de avanço e folga
axial] na página B15-70.
C7 (erro de distância percorrida: 0,05mm/300mm)
 Estudo da folga axial
Como o posicionamento é feito apenas na direção dada, a folga axial não é incluída na precisão no posicionamento. Consequentemente, não é necessário estudar a folga axial.
WTF2040: folga axial: 0,1 mm
WTF3060: folga axial: 0,14 mm
 Estudo da rigidez axial
Como a direção da carga não muda, não é necessário estudar a precisão no posicionamento baseado na rigidez axial.
 Estudo da transferência térmica pela geração de calor
 Estudo da mudança de orientação durante o percurso
Como o centro do fuso de esferas está a 150 mm de distância do ponto onde a maior precisão é
necessária, é preciso fazer estudar a mudança de orientação durante o percurso.
Suponha que o passo possa ser feito em 10 segundos devido à estrutura. O erro no posicionamento devido ao passo é obtido da seguinte maneira:
a = ℓ× sin
= 150 × sin (10´´)
=  0,007 mm
Portanto, a precisão no posicionamento (p) é obtida da seguinte maneira:
Δp =
0,05× 1000
300
0,007 + 0,06 = 0,234 mm
Uma vez que os modelos WTF2040-2, WTF2040-3, WTF3060-2 e WTF3060-3 atendem aos requisitos de seleção pelo processo de estudo da seção [Seleção de precisão do ângulo de avanço e
folga axial] na página B15-70 até a seção [Estudo da precisão no posicionamento] na página B15-79, o WTF2040-2, modelo mais compacto, é selecionado.
B15-79
Fuso de esferas
Suponha que o aumento na temperatura durante o funcionamento seja de 5C.
A precisão no posicionamento com base no aumento de temperatura é obtida da seguinte maneira:
ℓ = ×t ×ℓ
= 12 × 10‒6× 5 × 1000
= 0,06 mm
510BZ
[Estudo do torque de rotação]
 Torque de atrito devido à carga externa
O torque de atrito é obtido da seguinte maneira:
T1 =
Fa •Ph
17× 40
•A =
× 1 = 120 N •mm
2π •η
2 ×π × 0,9
 Torque devido à pré-carga no fuso de esferas
O fuso de esferas não é fornecido com uma pré-carga.
 Torque necessário para aceleração
Momento de inércia
Como o momento de inércia por comprimento da unidade do eixo é 1,23 × 10-3 kg•cm2/mm (consulte
a tabela de especificações), o momento de inércia do eixo com comprimento total de 1200 mm é
obtido da maneira a seguir.
Js = 1,23 × 10‒3× 1200 = 1,48 kg • cm2
= 1,48 × 10‒4 kg • m2
J = (m1 + m2)
(
2
2
Ph
40
2
–6
2
2
–6
–4
2
• A × 10 +Js • A = (60+20)
×1 ×10 + 1,48×10 ×1
2×π
2× π
(
)
–3
= 3,39 ×10 kg• m
)
2
Aceleração angular:
ω′ =
2π• Nm
2π×1500
2
60• t1 = 60×0,15 = 1050 rad/s
Com base nos dados acima, o torque necessário para aceleração é obtido da seguinte maneira.
T2 = (J + Jm) ×´ = (3,39 × 10‒3 + 1 × 10‒3) × 1050 = 4,61N • m
= 4,61 × 103 N • mm
Portanto, o torque necessário é especificado da seguinte maneira.
Durante a aceleração
Tk = T1 + T2 = 120 + 4,61×103 = 4730 N • mm
Durante movimento uniforme
Tt = T1 = 120 N • mm
Durante desaceleração
Tg = T1‒ T2 = 120 ‒ 4,61×103 = ‒ 4490 N • mm
B15-80
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
[Estudo do motor propulsor]
 Velocidade de rotação
Como o avanço do fuso de esferas é selecionado com base na velocidade nominal de rotação do
motor, não é necessário estudar a velocidade do motor.
Velocidade máxima de funcionamento de rotação: 1500 min‒1
: 3000 min‒1
Velocidade nominal de rotação do motor
 Quantidade mínima de alimentação
Assim como a velocidade de rotação, o avanço do fuso de esferas é selecionado com base no codificador normalmente utilizado para o servomotor CA. Portanto, não é necessário estudar esse fator.
Resolução do codificador: 1000 p/rev.
Dobrado: 2000 p/rev
 Torque do motor
O torque durante a aceleração calculado na seção [Estudo do torque de rotação] na página
B15-80 é o torque máximo necessário.
Tmax = 4730 N • mm
Portanto, o torque instantâneo máximo do servomotor CA precisa ser, no mínimo, 4.730 N-mm.
 Valor efetivo do torque
2
Trms
Tk
t1
Tt
t1
1305 N mm
2
t2
t2
2
Tg t3
t3 t4
2
Ts
t4
4730
2
2
2
0,15 120
0,85 4490
0,15 0,85 0,15 2,6
0,15
0
B15-81
Fuso de esferas
Os requisitos de seleção e o torque calculado na seção [Estudo do torque de rotação] na página
B15-80 podem ser descritos da seguinte maneira.
Durante a aceleração:
Tk = 4730 N • mm
t1 = 0,15 s
Durante movimento uniforme:
Tt = 120 N • mm
t2 = 0,85 s
Durante desaceleração:
Tg = 4490 N • mm
t3 = 0,15 s
Quando parado:
TS = 0
t4 = 2,6 s
O torque efetivo é obtido da seguinte maneira, e o torque nominal do motor deve ser 1305 N•mm
ou maior.
510BZ
 Momento de inércia
O momento de inércia aplicado ao motor é igual ao momento de inércia calculado na seção [Estudo
do torque de rotação] na página B15-80.
J = 3,39 × 10‒3 kg • m2
Normalmente, o motor necessita de um momento de inércia de, no mínimo, um décimo do momento de inércia aplicado à ele, embora o valor específico varie de acordo com o fabricante do motor.
Portanto, o momento de inércia do servomotor CA deve ser 3,39 × 10‒4kg-m2 ou maior.
A seleção está completa.
B15-82
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
Sistema transportador vertical
600
m2
Fuso de esferas
[Condições de seleção]
Massa da mesa
m1 = 40 kg
Massa de trabalho
m2 = 10 kg
Comprimento do curso ℓs = 600 mm
Velocidade máxima
Vmax = 0,3 m/s
Tempo de aceleração t1 = 0,2 s
Tempo de desaceleração t3 = 0,2 s
Número de recíprocas por minuto
n = 5 min-1
Folga
0,1 mm
Precisão no posicionamento 0,7 mm/600 mm
Repetição de precisão no posicionamento
0,05 mm
Quantidade mínima de alimentação s = 0,01 mm/pulso
Vida útil
20000 h
Motor propulsor
servomotor CA
Velocidade nominal de rotação: 3.000 min-1
Momento de inércia do motor
Jm = 5×10‒5 kg•m2
Engrenagem de redução Nenhuma (acoplamento direto)
Coeficiente de atrito da superfície do guia
 = 0,003 (rolamento)
Resistência da superfície do guia
f = 20 N (sem carga)
m1
[Itens de seleção]
Diâmetro do eixo
Avanço
Nº do modelo da castanha
Precisão
Folga axial
Método de suporte do eixo
Motor propulsor
B15-83
510BZ
[Seleção de precisão do ângulo de avanço e folga axial]
 Seleção de precisão do ângulo de avanço
Para obter precisão no posicionamento de 0,7 mm/600 mm:
±0,35
±0,7
=
600
300
A precisão do ângulo de avanço deve ser 0,35 mm/300 mm ou maior.
Logo, o grau de precisão do fuso de esferas (consulte a Tabela1 na página B15-20) precisa
ser C10 (erro de distância percorrida: 0,21 mm/300 mm).
O grau de precisão C10 está disponível para fusos de esferas laminados de baixo custo. Suponha
que um fuso de esferas laminado foi selecionado.
 Seleção da folga axial
A folga necessária é de 0,1 mm ou menor. No entanto, como uma carga axial é constantemente
aplicada em uma única direção com a montagem vertical, a carga axial não serve como folga, independente de seu tamanho.
Portanto, um fuso de esferas laminado de baixo custo é selecionado, uma vez que não haverá problema com a folga axial.
[Seleção de um eixo]
 Suposição do comprimento do eixo
Suponha que o comprimento total da castanha seja 100 mm e o comprimento da ponta do eixo seja
100 mm.
Portanto, o comprimento total é determinado pelo modelo a seguir, baseado no comprimento de
curso de 600 mm.
600 + 200 = 800 mm
Portanto, o comprimento do eixo será de 800 mm.
 Seleção do avanço
Com a velocidade nominal de rotação do motor propulsor sendo 3.000 min‒1 e a velocidade máxima
sendo 0,3 m/s, o avanço do fuso de esferas é obtido da maneira a seguir:
0,3×60×1000
= 6 mm
3000
Portanto, é necessário selecionar um tipo com avanço de 6 mm ou maior.
Além disso, o fuso de esferas e o motor podem ser montados em acoplamento direito, utilizando
uma engrenagem de redução. A resolução mínima por rotação de um servomotor CA é obtida baseada na revolução do codificador (1.000 p/rev; 1.500 p/rev) fornecido como acessório padrão para o
servomotor CA, conforme indicado abaixo.
1000 p/rev (sem multiplicação)
1500 p/rev (sem multiplicação)
2000 p/rev (dobrado)
3000 p/rev (dobrado)
4000 p/rev (quadruplicado)
6000 p/rev (quadruplicado)
B15-84
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
Para cumprir a quantidade mínima de alimentação de 0,010 mm/pulso, que é o requisito de seleção, os dados abaixo devem ser aplicados.
Avanço
6 mm —— 3000 p/rev
8 mm —— 4000 p/rev
10 mm —— 1000 p/rev
20 mm —— 2000 p/rev
40 mm —— 2000 p/rev
No entanto, com o avanço de 6 mm ou 8 mm, a distância de alimentação é de 0,002 mm/pulso, e o pulso
inicial do centro de controle que emite os comandos para o controlador do motor precisa ser, no mínimo,
150 kpps, e o custo do centro de controle pode ser mais alto.
Além disso, se o avanço do fuso de esferas for maior, o torque necessário para o motor também será
maior, resultando em um custo também maior.
Portanto, selecione 10 mm para o avanço do fuso de esferas.
 Seleção do diâmetro do eixo
 Seleção de um método de suporte de eixo
Como o fuso de esferas pressuposto possui um comprimento de curso de 600 mm e opera na velocidade máxima de 0,3 m/s (velocidade de rotação do fuso de esferas: 1.800 min-1), selecione a
configuração fixo-apoiado para o apoio do eixo.
B15-85
Fuso de esferas
Os modelos de fusos de esferas que atendem ao requisito de avanço de 10 mm, conforme descrito
na seção [Seleção de precisão do ângulo de avanço e folga axial] na página B15-84 e na
seção [Seleção de um eixo] na página B15-84 (consulte a Tabela20 na página B1535) são os seguintes.
Diâmetro do eixo Avanço
15 mm —— 10 mm
20 mm —— 10 mm
25 mm —— 10 mm
Consequentemente, a combinação de eixo de 15 mm de diâmetro e avanço de 10 mm é selecionada.
510BZ
 Estudo da carga axial permitida
Cálculo da carga axial máxima
Resistência da superfície do guia f = 20 N (sem carga)
Massa da mesa
m1 = 40 kg
Massa de trabalho
m2 = 10 kg
Velocidade máxima
Vmax = 0,3 m/s
Tempo de aceleração
t1 = 0,2 s
Consequentemente, os valores requisitados são obtidos da maneira a seguir.
Aceleração
α=
Vmax
= 1,5 m/s2
t1
Durante a aceleração para cima:
Fa1 = (m1 + m2) •g + f + (m1 + m2) • = 585 N
Durante movimento uniforme para cima:
Fa2 = (m1 + m2) •g + f = 510 N
Durante a desaceleração para cima:
Fa3 = (m1 + m2) •g + f ‒ (m1 + m2) • = 435 N
Durante a aceleração para baixo:
Fa4 = (m1 + m2) •g ‒ f ‒ (m1 + m2) • = 395 N
Durante movimento uniforme para baixo:
Fa5 = (m1 + m2) •g ‒ f = 470 N
Durante a desaceleração para baixo:
Fa6 = (m1 + m2) •g ‒ f + (m1 + m2) • = 545 N
Portanto, a carga axial máxima aplicada no fuso de esferas é a seguinte:
Famax = Fa1 = 585 N
Carga de flambagem do eixo
Fator de acordo com o método de montagem
Supondo que o método de montagem da seção entre
gem deve ser considerada, é “fixo-fixo: “
Distância entre as duas superfícies de montagem
Diâmetro menor da rosca do eixo
2=20 (consulte B15-38)
a castanha e o mancal, onde a flambaℓa=700 mm (estimativa)
d1=12,5 mm
4
P1 = η2 •
4
d1
4
4
12.5
2 × 10 = 20×
2 × 10 = 9960 N
ℓa
700
Carga de compressão e tensão permitidas do eixo
P2 = 116d12 = 116 × 12,52 = 18100 N
Portanto, a carga de flambagem e a carga de compressão e tensão permitidas do eixo são, ao
menos, iguais à carga axial máxima. Consequentemente, um fuso de esferas que atenda a esses
requisitos pode ser utilizado sem problemas.
B15-86
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
 Estudo da velocidade de rotação permitida
Velocidade máxima de rotação
● Diâmetro do eixo: 15 mm; avanço: 10 mm
Velocidade máxima
Avanço
Vmax= 0,3 m/s
Ph= 10 mm
3
Nmax =
Vmax × 60× 10
–1
= 1800 min
Ph
Velocidade de rotação permitida determinada pela velocidade perigosa do eixo
Fator de acordo com o método de montagem
2=15,1 (consulte B15-40)
Supondo que o método de montagem para a seção entre a castanha e o mancal, onde a velocidade perigosa deve ser considerada, é “fixo-fixo: ”
ℓb=700 mm (estimativa)
Distância entre duas superfícies de montagem
● Diâmetro do eixo: 15 mm; avanço: 10 mm
Diâmetro menor da rosca do eixo
d1=12,5 mm
N1 = λ2×
d1
7
7
–1
12,5
10 = 15,1×
2 × 10 = 3852 min
2
700
ℓb
N2 =
Fuso de esferas
Velocidade de rotação permitida determinada pelo Valor DN
● Diâmetro do eixo: 15 mm; avanço: 10 mm (fuso de esferas de avanço amplo)
Diâmetro da esfera de centro a centro
D=15,75 mm
–1
70000
70000
=
= 4444 min
D
15,75
Portanto, os requisitos de velocidade perigosa e valor DN do eixo são atendidos.
B15-87
510BZ
[Seleção de castanha]
 Seleção de um número de modelo de castanha
O fuso de esferas laminado com eixo de 15 mm de diâmetro e avanço de 10 mm é o modelo de
fuso de esferas laminado de avanço amplo a seguir.
BLK1510-5,6
(Ca=9,8 kN, C0a=25,2 kN)
 Estudo da carga axial permitida
Supondo que a carga de impacto é aplicada durante a aceleração e desaceleração, defina o fator
de segurança estática (fS) como 2 (consulte Tabela1 na página B15-47).
Famax =
C 0a
25,2
=
= 12,6 kN = 12600 N
fS
2
A carga axial permitida obtida é maior que a carga axial máxima de 585 N. Portanto, não ocorrerão
problemas com esse modelo.
 Estudo da vida útil de serviço
Cálculo da distância percorrida
Velocidade máxima
Vmax= 0,3 m/s
Tempo de aceleração
t1 = 0,2 s
Tempo de desaceleração t3 = 0,2 s
● Distância percorrida durante a aceleração
ℓ1, 4 =
Vmax • t1
2
× 103 =
0,3× 0,2
× 103 = 30 mm
2
● Distância percorrida durante o movimento uniforme
ℓ2, 5 = ℓS –
Vmax • t1 + Vmax • t3
2
× 103 = 600 –
0,3 × 0,2 + 0,3 ×0,2
× 103 = 540 mm
2
● Distância percorrida durante a desaceleração
ℓ3, 6 =
Vmax • t3
2
× 103 =
0,3 ×0,2
× 103 = 30 mm
2
Com base nas condições acima, a relação entre a carga axial aplicada e a distância percorrida é
mostrada na tabela abaixo.
Movimento
Carga axial aplicada Distância percorrida
ℓN(mm)
FaN(N)
N° 1: Durante a aceleração para cima
585
30
N° 2: Durante movimento uniforme para cima
510
540
30
N° 3: Durante a desaceleração para cima
435
N° 4: Durante a aceleração para baixo
395
30
N° 5: Durante movimento uniforme para baixo
470
540
N° 6: Durante a desaceleração para baixo
545
30
＊ O subscrito (N) indica um número de movimentos.
B15-88
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
Carga axial média
3
Fm =
3
3
3
3
3
3
1
(Fa1 •ℓ1 + Fa2 •ℓ2 + Fa3 •ℓ3 + Fa4 •ℓ4 + Fa5 •ℓ5 + Fa6 •ℓ6) = 492 N
2× ℓS
Vida nominal
Capacidade de carga nominal
Fator de carga
Carga média
Vida nominal
L=
(
Ca
fw · Fm
3
)
6
× 10 =
(
9800
1,5 × 492
Média de revoluções por minuto
Número de recíprocas por minuto
Curso
Avanço
Nm =
Ca= 9800 N
fW= 1,5 (consulte a Tabela2 na página B15-48)
Fm= 492 N
L (rev)
3
) ×10 = 2,34 ×10 rev
6
9
n = 5 min-1
ℓS= 600 mm
Ph= 10 mm
2 ×n ×ℓs
2 × 5× 600
=
= 600 min–1
10
Ph
Lh =
L
60 • Nm
=
2,34×109
= 65000 h
60× 600
Calculando a vida útil de serviço na distância percorrida com base na vida nominal
Vida nominal
L=2,34×109 rev
Avanço
Ph= 10 mm
LS = L × Ph × 10-6 = 23400 km
De acordo com todas as condições descritas acima, o modelo BLK1510-5,6 satisfaz o tempo de
vida útil desejado de 20.000 horas.
B15-89
Fuso de esferas
Calculando a vida útil de serviço com base na vida nominal
Vida nominal
L=2,34×109 rev
Média de revoluções por minuto
Nm = 600 min-1
510BZ
[Estudo da rigidez]
Como as condições para seleção não incluem rigidez e esse elemento não é particularmente necessário, ele não será descrito aqui.
[Estudo da precisão no posicionamento]
 Estudo da precisão do ângulo de avanço
A classe C10 de precisão foi selecionada na seção [Seleção de precisão do ângulo de avanço e
folga axial] na página B15-84.
C10 (erro de distância percorrida: 0,21 mm/300 mm)
 Estudo da folga axial
Como a carga axial está sempre presente em uma direção dada somente por causa da montagem
vertical, não é necessário estudar a folga axial.
 Estudo da rigidez axial
Como a precisão do ângulo de avanço é obtida após a precisão no posicionamento requisitada, não
é necessário estudar a precisão no posicionamento determinada pela rigidez axial.
 Estudo da transferência térmica pela geração de calor
Como a precisão do ângulo de avanço é obtida após a precisão no posicionamento requisitada, não
é necessário estudar a precisão no posicionamento determinada pela geração de calor.
 Estudo da mudança de orientação durante o percurso
Como a precisão do ângulo de avanço é obtida em um nível bem mais avançado que a precisão no
posicionamento requisitada, não é necessário estudar a precisão no posicionamento.
[Estudo do torque de rotação]
 Torque de atrito devido à carga externa
Durante movimento uniforme para cima:
T1 =
510× 10
Fa2 • Ph
=
= 900 N• mm
2× π ×η
2× π ×0,9
Durante movimento uniforme para baixo:
T2 =
470× 10
Fa5• Ph
=
= 830 N•mm
2× π×η
2× π ×0,9
 Torque devido à pré-carga no fuso de esferas
O fuso de esferas não é fornecido com uma pré-carga.
B15-90
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
 Torque necessário para aceleração
Momento de inércia:
Como o momento de inércia por comprimento da unidade do eixo é 3,9 × 10-4 kg•cm2/mm (consulte
a tabela de especificações), o momento de inércia do eixo com comprimento total de 800 mm é obtido da seguinte maneira.
JS = 3,9 × 10‒4× 800 = 0,31 kg • cm2
= 0,31 × 10‒4 kg • m2
J = (m1 + m2)
(
2
2
Ph
10
2
–6
2
2
–6
–4
2
• A × 10 +Js • A = (40+10)
×1 ×10 + 0,31×10 ×1
2×π
2 ×π
)
–4
= 1,58 × 10 kg• m
(
)
2
Aceleração angular:
ω′ =
2π • Nmax
2π× 1800
= 60× 0,2 = 942 rad/s2
60• t
B15-91
Fuso de esferas
Com base nos dados acima, o torque necessário para aceleração é obtido da seguinte maneira.
T3 = (J + Jm) •´ = (1,58 × 10‒4 + 5 × 10‒5) × 942 = 0,2 N•m = 200 N•mm
Portanto, o torque necessário é especificado da seguinte maneira.
Durante a aceleração para cima:
Tk1 = T1 + T3 = 900 + 200 = 1100 N•mm
Durante movimento uniforme para cima:
Tt1 = T1 = 900 N•mm
Durante a desaceleração para cima:
Tg1 = T1‒ T3 = 900 ‒ 200 = 700 N•mm
Durante a aceleração para baixo:
Tk2 = 630 N•mm
Durante movimento uniforme para baixo:
Tt2 = 830 N•mm
Durante a desaceleração para baixo:
Tg2 = 1030 N•mm
510BZ
[Estudo do motor propulsor]
 Velocidade de rotação
Como o avanço do fuso de esferas é selecionado com base na velocidade nominal de rotação do
motor, não é necessário estudar a velocidade do motor.
Velocidade máxima de funcionamento de rotação: 1800 min‒1
: 3000 min‒1
Velocidade nominal de rotação do motor
 Quantidade mínima de alimentação
Assim como a velocidade de rotação, o avanço do fuso de esferas é selecionado com base no codificador normalmente utilizado para o servomotor CA. Portanto, não é necessário estudar esse fator.
Resolução do codificador: 1000 p/rev.
 Torque do motor
O torque durante a aceleração calculado na seção [Estudo do torque de rotação] na página
B15-90 é o torque máximo necessário.
Tmax = Tk1 = 1100 N•mm
Portanto, o torque de pico máximo do servomotor CA precisa ser, no mínimo, 1100 N-mm.
 Valor efetivo do torque
Os requisitos de seleção e o torque calculado na seção [Estudo do torque de rotação] na página
B15-90 podem ser descritos da seguinte maneira.
Durante a aceleração para cima:
Tk1 = 1100 N•mm
t1 = 0,2 s
Durante movimento uniforme para cima:
Tt1 = 900 N•mm
t2 = 1,8 s
Durante a desaceleração para cima:
Tg1 = 700 N•mm
t3 = 0,2 s
Durante a aceleração para baixo:
Tk2 = 630 N•mm
t1 = 0,2 s
Durante movimento uniforme para baixo:
Tt2 = 830 N•mm
t2 = 1,8 s
Durante a desaceleração para baixo:
Tg2 = 1030 N•mm
t3 = 0,2 s
Quando parado(m2=0):
TS = 658 N•mm
t4 = 7,6 s
B15-92
510BZ
Diagrama de seleção
Exemplos de seleção de fuso de esferas
O torque efetivo é obtido da seguinte maneira, e o torque nominal do motor deve ser 743 N•mm ou
maior.
Trms =
Tk12 • t1 ＋ Tt12 • t2＋ Tg12 • t3＋ Tk22 • t1＋ Tt22 • t2＋ Tg22 •t3＋Ts2 •t4
t1 ＋ t2 ＋ t3＋ t1＋ t2 ＋ t3＋ t4
11002 ×0,2＋9002 ×1,8＋7002 ×0,2＋6302 ×0,2＋8302 ×1,8＋10302 ×0,2＋6582 ×7,6
0,2 ＋ 1,8 ＋ 0,2 ＋ 0,2 ＋ 1,8＋ 0,2＋7,6
= 743 N• mm
=
 Momento de inércia
O momento de inércia aplicado ao motor é igual ao momento de inércia calculado na seção [Estudo
do torque de rotação] na página B15-90.
J = 1,58 × 10‒4 kg • m2
Normalmente, o motor necessita de um momento de inércia de, no mínimo, um décimo do momento de inércia aplicado à ele, embora o valor específico varie de acordo com o fabricante do motor.
Portanto, o momento de inércia do servomotor CA deve ser 1,58 × 10‒5kg-m2 ou maior.
A seleção está completa.
Fuso de esferas
B15-93
510BZ
B15-94