Característica dos Geradores de Corrente e Máxima transferência

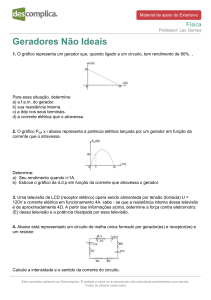
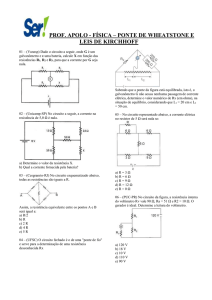
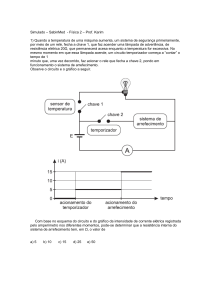
Departamento de Física e Química – Curso de Física
Laboratório de Competências Experimentais II
Característica dos Geradores de Corrente e Máxima transferência de Potência
Objetivos
Analisar o comportamento de um gerador de corrente contínua, quando alimentando um circuito resistivo
Introdução
Quando geramos energia elétrica estamos na verdade transformando algum tipo de energia (química,
mecânica, nuclear, térmica, etc) em energia elétrica.
O dispositivo que faz tal transformação chama-se gerador. Duas das mais importantes características do
gerador, são:
- sua força eletromotriz (fem), símbolo ;
- sua resistência interna, símbolo r.
Podemos escrever:

W W

q it
(8.1)
ou seja, a fem, ou eletromotância é a razão entre a energia transformada no gerador, e a quantidade de carga
elétrica posta em circulação. Se o gerador converte a energia W no intervalo de tempo t , mantendo uma
corrente i, as fórmulas acima definem perfeitamente a eletromotância.
Um gerador fornece uma potência dada por:
P
W
 P  i
t
(8.2)
Vamos analisar o circuito abaixo:
A
i
R
r
gerador

i
B
O circuito tem gerador de eletromotância . Mas como todo gerador, tem resistência interna r, e ainda é
ligado ao circuito externo, onde há a resistência R (carga).
O gerador proporciona ao circuito o aparecimento da corrente i. Devido à resistência interna r do gerador,
parte da energia gerada,é dissipada na forma de calor.
Vamos supor que o gerador produza uma quantidade de energia WG e perca, devido à dissipação na
resistência interna, uma quantidade de energia
seja, é cedido à R:
WG  Wr  WR
(8.3)
que pode ser escrito como:
q  ri2 t  Vq
(8.4)
ou ainda:
q  ri2 t  Vi t
  ri  V
(8.5)
Wr . Assim, só o que sobra é transferido ao circuito externo, ou
o que mostra que a tensão (V) disponível nos terminais do gerador é sempre menor que sua eletromotância. A
eletromotância
ε é medida em volts, assim como a tensão disponível V.
Procedimento
a) Material utilizado:
01 bateria 1,5V (que será o nosso gerador)
01 ponte de fio
01 voltímetro CC
01 miliamperímetro CC
01 resistor de 10 .
06 fios de ligação
b) Montagem:
V
10
mA
c) Descrição do experimento:
1. Monte o circuito esquematizado.
2. Deixe a ponte em posição de resistência máxima e feche o circuito.
3. Varie a posição do cursor, anotando valores de tensão e corrente.
QUESTÕES
1. Faça o gráfico V x i
2. No gráfico, procure o valor de V para i = 0. Compare este valor de V com o valor
indicado na bateria. O que
se conclui disto?
3. No gráfico, verifique o valor de i para V = 0. Qual o significado deste valor?
4. Calcule a inclinação do gráfico V x i e analise o seu significado.
5. Escreva a equação da curva obtida através do gráfico.
6. Pelo gráfico é possível saber se a resistência interna da pilha é constante? Explique.
7. Se você tivesse um circuito com vários geradores ligados entre si, a relação   ri  V ainda valeria?
Explique.
8. A tensão disponível nos terminais de uma bateria pode ser maior que, menor que, ou igual à sua
eletromotância? Explique.
9. Se a resistência interna do gerador fosse muito grande, o que aconteceria?
Objetivos
Traçar a curva característica da potência de um gerador e verificar, experimentalmente, a condição para a qual a
potência transferida pelo gerador é máxima.
Introdução
Um gerador real sempre apresenta perdas internas, resultantes das perdas ôhmicas na resistência interna total.
Assim, a tensão disponível para a carga (elemento colocado na saída do circuito, e que utilizará a tensão de
saída) é sempre menor que a eletromotância.
Definindo:
PU = Vi (Potência útil)
PG = εi (Potência gerada)
Pi = r i2 (Potência consumida internamente)
Tem-se:
PU = PG – Pi
(7.1)
Da equação do gerador (6.5) pode-se escrever:
PU = εi – ri2
(7.2)
A expressão (7.2) é a equação de uma parábola, que é representada no gráfico abaixo:
No gráfico definimos i0 como a corrente para a qual a potência útil é máxima. A corrente i cc é definida como a
corrente de curto circuito, que pode ser calculada fazendo PU = 0 na expressão (7.2): desta forma, tem-se:

r
i cc 
(7.3)
Esta corrente de curto circuito é a corrente obtida ligando o positivo do gerador ao negativo por meio de um fio de
resistência quase nula. Mas como é uma corrente muito grande, que pode danificar o gerador, é desaconselhável
que isto seja feito!
Deseja – se agora saber a condição na qual a maior potência será entregue ao circuito externo, representado pelo
resistor R. Para tal, analisa-se qual o máximo da função Pu. Representando esta função apenas por P temos:
P  Ri2
i

R r
P
R 2
R  r 
A condição de máximo ou de mínimo é dada por:
dP
0
dR
dP R  r   2  r 2 2R  r 

dR
R  r 4
2
R  r 2  0
dP
0
dR
R  r 3
Resolvendo a última equação, chega-se a: r  R ( 7.4 )
Na expressão de potência útil, ( 7.2 ), o ponto de máximo da curva é dado por i = i 0 e, como parábola é uma curva
simétrica, tem-se:
i

i  cc 
( 7.5 )
2
2r
Levando-se ( 7.5 ) em ( 7.2 ), tem-se:
Pu 
2
( 7.6 )
4r
Com o resultado acima em ( 7.5 )
V    ri 0  V0 

( 7.7 )
2
A expressão ( 7.7 ) define o valor da tensão disponível nos terminais do gerador na condição de máxima potência.
O subíndice usado em V indica para i = i0 . Define-se o redimento por:
n
Pu
( 7.8 )
Pg
Na situação de potência máxima o rendimento será:
n
V0i 0
 i0

V0  / 2

 0,5  50 %


Procedimento
a) Material utilizado:
01 Fonte Universal
01 Resistor de 10 
01 Voltímetro
01 Miliamperímetro
01 Caixa de Resistência
b) Montagem:
c) Descrição do experimento:
1. Usando o voltímetro, regule a tensão de saída da fonte para 5V.
2. Ajuste a caixa de resistências para os valores do quadro abaixo. Peça ao seu professor para
mostrar como se obtém uma determinada resistência. Para cada valor de R (resistência da carga)
meça e anote a tensão e a corrente em R.
R ()
V (volts)
I (mA)
PU (mW)
n (%)
100
80
60
40
20
10
8
4
1. Com os dados obtidos faça o gráfico Potência Útil versus corrente.
2. Determine graficamente a potência útil máxima e a corrente de curto circuito.
3.Trace o gráfico PU x R,
4. Para a condição de máxima potência determine, a partir de seus dados: r, V, e n.
2
1
0