Lista 5 - Plato

FEP 2195 - FÍSICA GERAL E EXPERIMENTAL I
LISTA DE EXERCÍCIOS Nº 5
1. Um vagão de montanha-russa de 1 000 kg está inicialmente no topo de uma subida, no ponto (A).
Ele se movimenta então 135 ft, a um ângulo de 40,0° abaixo da horizontal, até um ponto mais baixo (B).
a) Escolha o ponto (B) como nível zero para a energia potencial gravitacional. Encontre a energia
potencial do sistema vagão-Terra nos pontos (A) e (B) e a mudança na energia potencial na medida em
que o vagão se desloca.
b) Repita o item a), colocando o nível de referência zero no ponto (A).
2. Uma conta furada desliza sem atrito por um fio
que dá uma volta circular vertical (Figura à
esquerda). A conta é solta de uma altura
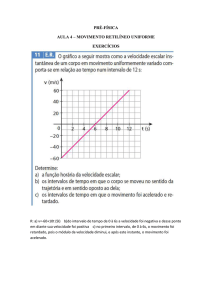
h = 3,50 R.
a) Qual é a velocidade escalar no ponto A ?
b) Qual é o valor da força normal sobre ela no
ponto A se sua massa é de 5,00 g ?
3. Um trapézio de circo consiste em uma barra
suspensa por duas cordas paralelas, cada uma
com comprimento l , permitindo aos trapezistas
balançar em um arco circular vertical (Figura à
direita).Suponha que uma trapezista de massa m
segure a barra e salte de uma plataforma elevada,
começando do repouso com as cordas a um ângulo
θi em relação à vertical. Suponha que o tamanho
da trapezista seja pequeno comparado com
comprimento L , que ela não faça o trapézio oscilar
mais alto e que a resistência do ar seja desprezível.
a) Mostre que quando as cordas fazem um ângulo θ
com a vertical, a trapezista tem de exercer uma
força de magnitude mg(3cosθ - 2cos θi) para ficar
pendurada.
b) Determine o ângulo
θi para o qual a força
necessária para se ficar pendurado na parte mais
baixa da oscilação seja de duas vezes o peso da
trapezista.
4. Uma força agindo sobre uma partícula em
movimento no plano xy é dada por F = (2y i + x 2j) N,
em que x e y estão em metros. A partícula se desloca
da origem até uma posição final com coordenadas x =
5,00 m e y = 5,00 m, como na Figura à direita. Calcule
o trabalho feito por F ao longo de:
a) OAC
b) OBC
c) OC
d) F é conservativa ou não conservativa? Explique.
5. Um corpo de 120g está ligado à extremidade inferior de uma mola não esticada nem comprimida. A
mola está dependurada verticalmente e tem uma constante elástica de 40,0 N/m. O corpo é solto.
a) Qual é sua velocidade escalar máxima?
b) Qual é a distância que ele cai até chegar momentaneamente ao repouso?
6. Determine para a curva de energia potencial
mostrada na Figura ao lado ,
a) Se a força Fx é positiva, negativa ou nula nos cinco
pontos indicados.
b) Indique pontos de equilíbrio estável, instável e
neutro.
c) Trace a curva para Fx de x = 0 até x = 9,5 m.
7. Uma partícula de massa de 1,18 kg está ligada
entre duas molas idênticas sobre uma mesa horizontal
sem atrito. As molas têm constante elástica k e cada
uma está inicialmente relaxada.
a) Se a partícula é puxada a uma distância x ao longo
de uma direção perpendicular à configuração inicial
das molas, como na Figura à esquerda, mostre que a
energia potencial do sistema é:
U(x) = kx2 + 2kL (L - )22Lx+
(Dica: Veja o Problema 50 no Capítulo 6)
b) Faça um gráfico de U(x) contra x e identifique todos
os pontos de equilíbrio. Suponha que L = 1,20 m e k =
40,0 N/m.
c) Se a partícula é puxada 0,500 m para a direita e
então solta qual será sua velocidade escalar quando
ela atinge a posição de equilíbrio em x = 0?
8. Um pula-pula de criança armazena energia em uma
mola com uma constante elástica de 2,50 x 10 4 N/m.
Na posição Ⓐ (xA =-0,100m), a compressão da mola é
máxima e a criança está momentaneamente em
repouso. Na posição Ⓑ (xB = 0), a mola está relaxada
e a criança está subindo. Na posição Ⓒ, a criança está
de novo momentaneamente em repouso no topo do
salto. A massa combinada da criança e do pula-pula é
de 25,0 kg.
a) Calcule a energia total do sistema se a energia
potencial gravitacional e a elástica são nulas x = 0.
b) Determine xC.
c) Calcule a velocidade escalar da criança em Ⓑ.
d) Determine o valor de
x para o qual a energia
cinética do sistema é um máximo.
e) calcule a velocidade escalar máxima da criança.
9. Um corpo de l,00 kg desliza para a direita sobre
uma superfície que tem coeficiente de atrito cinético de
0,250. O corpo tem velocidade escalar
vi=3,00 m/s
quando entra em contato com uma mola leve que tem
constante elástica de 5,00 N/m. O corpo atinge o
repouso após a mola ter sido comprimida uma
distância d.
O corpo é então forçado para a esquerda pela mola e
continua a se mover nessa direção além da posição da
mola relaxada,
Encontre:
a) a distância de compressão d;
b) a velocidade escalar v na posição relaxada quando
o corpo está em movimento para a esquerda;
c) a distância D.
10. Um vagão de montanha-russa é solto do repouso
no topo da primeira subida e então se desloca
livremente com atrito desprezível. A montanha-russa
mostrada na "figura abaixo" tem uma volta circular de
raio R em um plano vertical.
a) Suponha primeiro que o vagão por pouco não deixe
de dar a volta na pista: no topo da pista os
passageiros estão de cabeça para baixo e se sentem
sem peso. Encontre a altura necessária do ponto
inicial acima da base da volta, em termos de R.
b) Suponha agora que o ponto de início esteja na
altura necessária mínima ou acima dela. Mostre que a
força normal sobre o vagão na parte inferior da pista
excede a força normal no topo da volta por seis vezes
o peso do vagão. A força normal sobre cada
passageiro segue a mesma regra. Uma força normal
tão grande é perigosa e muito desconfortável para os
passageiros. Por esse motivo as montanhas-russas
não são construídas com voltas circulares em planos
verticais.
11. Uma partícula de 3,00 kg tem uma velocidade de (3,00i - 4,00j) m/s.
a) Encontre as componentes x e y do momento.
b) Encontre o módulo e a direção do seu momento.
12. Qual é a velocidade que você pode fornecer à Terra? Em particular, quando você pula para cima o
mais alto que consegue, qual é a ordem de grandeza da velocidade escalar de recuo máxima que você
pode fornecer à Terra? Modele a Terra como um corpo perfeitamente sólido.
Na sua solução, informe as grandezas físicas que você supõe como dados, e os valores que você
mede ou estima para elas.
13. Uma boa de aço de 3,00 kg atinge uma parede
com velocidade escalar de 10,0 m/s a um ângulo de
60° com a superfície. Ela é refletida com a mesma
velocidade escalar e com o mesmo ângulo .
Se a bola fica em contato com a parede por 0,200 s,
qual é a força média exercida sobre a bola pela
parede?
14. Em um jogo de softbol, uma bola de 0,200 kg chega ao batedor com 15,0 m/s a um ângulo de 45,0°
abaixo da horizontal. O batedor lança a bola para o centro do campo, fornecendo-lhe uma velocidade
de 40,0 m/s a 30,0° acima da horizontal.
a) Determine o impulso fornecido à bola.
b) Se a força sobre a bola aumenta linearmente por 4,00ms, fica constante por 20,0ms, e então diminui
a zero linearmente em outros 4,00ms, qual é a força máxima sobre a bola?
15. Uma chapa uniforme de aço tem o formato da
figura ao lado.
Calcule as coordenadas x e y do centro de massa da
peça.
16. Uma barra de comprimento de 30,0 cm tem densidade linear (massa por unidade de comprimento)
dada por:
λ= 50,00 g/m + (20,0 g/m2)x
x é à distância a partir de uma extremidade, medida em metros.
a) Qual é a massa da barra?
b) O centro de massa está a qual distância da extremidade x = 0?
17. Considere um sistema de duas partículas no plano x-y:
m1 = 2,00 kg está na posição r1 = (1,00i + 2,00j)m e tem velocidade de
(3,00i + 0,500j) m/s; m2 = 3,00 kg está em r2 = (-4,00i - 3,00j)m e tem velocidade de (3,00i - 2,00j) m/s.
a) Represente essas partículas sobre um papel quadriculado ou de gráfico. Trace seus vetores posição
e mostre suas velocidades.
b) Encontre a posição do centro de massa do sistema e marque-o sobre o gráfico.
c) Determine a velocidade do centro de massa e mostre-a também sobre o diagrama.
d) Qual é o momento linear total do sistema?
18. Romeu (77,0 kg) diverte Julieta (55,0 kg) tocando seu violão da parte de trás de seu barco em
repouso na água parada, afastado, 2,70 m de Julieta, que está na parte dianteira do barco
. Após a serenata, Julieta desloca-se cuidadosamente para a parte de trás do barco (afastando-se da
margem) para dar um beijo no rosto de Romeu.
Qual é a distância que o barco de 80,0 kg se desloca em direção à margem?
Para se manter informado, visite constantemente o site:
http://plato.if.usp.br/1-2006/fep2195d