Termoquímica. A 1ª Lei da termodinâmica e cálculos entálpicos

Termoquímica. A 1ª Lei da termodinâmica e cálculos entálpicos
Texto de Apoio com problemas resolvidos e propostos
Fernando M.S. Silva Fernandes
Departamento de Química e Bioquímica, FCUL
1. Introdução
A Termodinâmica estuda as transferências de energia entre um dado sistema e os seus
arredores, as conversões entre os diferentes tipos de energia e as relações entre as
propriedades dos sistemas em equilíbrio.
Energia é um conceito primitivo que traduz intuitivamente a capacidade para produzir
trabalho. É definida através de relações funcionais entre propriedades físicas de
significado preciso e que podem ser medidas experimentalmente. Por exemplo, a
energia cinética, Ec, dum corpo material A é uma função das suas massa, MA, e
velocidade, v :
Ec = 1/2 MA v2
(1)
Existem dois processos fundamentais de transferência de energia: trabalho e calor.
Trabalho é outro conceito primitivo que traduz intuitivamente o esforço realizado no
deslocamento dum corpo por efeito duma força aplicada. Se a força constante, f, tiver
a direcção do deslocamento ∆r, o trabalho realizado, ∆W, define-se como:
∆W = f ∆r
(2)
A expressão anterior traduz quantitativamente a noção intuitiva de que o trabalho é
tanto maior quanto maiores forem a força aplicada e o caminho percorrido.
O trabalho realizado pela força de 1N (Newton) através do deslocamento de 1m
(metro) designa-se por 1J (Joule). Se este trabalho for efectuado sobre o corpo de
massa MA para aumentar a sua velocidade, dizemos que o corpo adquiriu 1J de
energia cinética, isto é, 1J de energia foi transferida para o corpo por efeito da
realização de trabalho.
*******************************
Como se justifica a expressão (1) para a energia cinética? Suponhamos um corpo em
movimento, de massa M, que num dado instante tem a posição r1 e a velocidade v1.
Aplica-se ao corpo uma força externa constante f = M a (de acordo com uma das leis
de Newton; a é a aceleração) até que o corpo atinja a posição r2, ao fim do intervalo
de tempo t. A velocidade na posição r2 será v2 = a t + v1 (a aceleração é constante)
donde a = (v2-v1)/t. Por outro lado, a posição r2 = ½ a t2 + v1 t + r1, donde o
deslocamento sofrido pelo corpo durante a actuação da força é, considerando as
expressões anteriores:
∆r = r2 – r1 = ½ a t2 + v1 t = ½ (v2-v1) t + v1 t = ½ (v2+v1) t
Uma vez que o trabalho realizado é igual à força vezes o deslocamento:
∆W = M a (r2 – r1) = ½ M (v2-v1) (v2+v1) = ½ M v 22 - ½ M v12
Isto é, o trabalho realizado sobre o corpo alterou a sua energia cinética ½ M v2. Por
outras palavras: energia foi transferida para o sistema através da realização de
trabalho.
***************************************
Figura 1.1. Conversão de energia cinética em energia potencial gravítica
A energia cinética de 1J (ou outro valor qualquer) adquirida pelo corpo A considerado
atràs pode, por sua vez, ser totalmente utilizada para realizar trabalho se o corpo
diminuir a sua velocidade até atingir o repouso. Por exemplo, através dum mecanismo
apropriado ligado ao corpo (ver figura 1.1), pode proceder-se à elevação de uma outra
massa, MB, até à altura h. Isto significa que 1J de energia cinética do corpo A se
converte, através da realização de trabalho contra a força da gravidade, em 1J de
energia potencial gravítica, Ep, do corpo B, a qual se define como:
Ep = MB g h
onde g é a aceleração da gravidade.
2
(3)
**************************************
A expressão anterior tem uma justificação análoga à da energia cinética. A força que a
Terra exerce sobre um corpo de massa M (o peso do corpo ou a força da gravidade) é
M g. Assim, para elevar o corpo até à altura h (o deslocamento) é necessário exercer
uma força igual, mas oposta, à força da gravidade. Portanto, o trabalho realizado
sobre o corpo é M g h (força x deslocamento). Dizemos, então, que através da
realização de trabalho o corpo adquiriu a energia potencial gravítica M g h,
exactamente igual ao trabalho realizado.
Note-se a diferença entre energia cinética e energia potencial. A primeira implica
movimento (velocidade) enquanto a segunda diz respeito à posição de um corpo em
relação a outro. Por outro lado, pode parecer que a energia adquirida por um corpo é
sempre igual ao trabalho realizado sobre ele. Vamos ver que nem sempre é assim. De
facto, um sistema pode adquirir energia por outro processo de transferência diferente:
o calor.
***************************************
As considerações anteriores sugerem que a energia é uma entidade que se conserva ao
longo dos processos: a realização de 1J de trabalho deu lugar a 1J de energia cinética
que, por sua vez, se converteu em 1J de energia potencial gravítica e, assim,
sucessivamente. Por outras palavras, a energia não se cria “a partir do nada”, não se
destroi, apenas se transforma e se transfere. A conservação da energia constitui a 1ª
Lei da Termodinâmica, a qual trataremos adiante.
Os corpos analisados anteriormente foram considerados como um todo, sem
referência à sua constituição interna. A energia da expressão (1) é a energia cinética
translacional do corpo A como um todo e a energia da expressão (2) é a energia de
interacção corpo B – Terra, ou seja, a energia potencial gravítica do corpo.
Designaremos a soma destas energias como energia externa. Sob o ponto de vista
termoquímico, no entanto, é essencial considerar, também, a energia interna dum
dado corpo. Como sabemos, todos os corpos materiais são constituídos por moléculas
e átomos (os quais, por sua vez, são constituídos por electrões e núcleos) em
movimento e interacção incessantes. Assim, teremos de considerar os diferentes tipos
de energia molecular: energia cinética translacional, energia potencial intermolecular,
energia rotacional, energia vibracional, energia electrónica, energia nuclear, etc. A
energia interna do sistema é a soma dessas diferentes contribuições energéticas.
Por exemplo, num sistema constituído por N moléculas, a contribuição da energia
cinética translacional para a energia interna total é dada por:
N
1
K = ∑ m i v i2
i =1 2
3
(4)
onde mi é a massa do átomo i e vi a sua velocidade. Uma vez que os átomos colidem
entre si, as respectivas velocidades têm diferentes direcções e sentidos. A energia
cinética interna está, assim, numa forma desordenada (caótica) e designa-se
usualmente por energia térmica.
Se as moléculas forem de argon (um elemento do grupo 18 da Tabela Periódica, cujas
molécula são monoatómicas) a energia potencial entre dois átomos é dada,
aproximadamente, pelo chamado potencial de Lennard-Jones:
⎡⎛ σ ⎞12 ⎛ σ ⎞6 ⎤
u(r) = 4ε ⎢⎜ ⎟ − ⎜ ⎟ ⎥
⎝ r ⎠ ⎥⎦
⎢⎣⎝ r ⎠
(5)
onde ε é o fosso do potencial , σ o diâmetro atómico e r a distância entre dois átomos,
conforme representado na figura 2.1.
****************************************
Note-se que a energia anterior está relacionada (de modo análogo ao da energia
potencial gravítica) com a posição de um átomo em relação ao outro medida pela
distância r o que, como já referimos, caracteriza a energia potencial. Neste caso, a
energia é igual ao trabalho realizado para aproximar dois átomos, inicialmente a uma
distância infinita, até à distância finita r . As forças em jogo são, agora, de natureza
electromagnética e têm origem na estrutura atómica das espécies consideradas.
**************************************
Figura 2.1. Potencial de Lennard-Jones
A energia potencial interatómica total de N átomos é, então, a soma das energias dos
pares diferentes de átomos:
4
N −1 N
U = ∑ ∑ u ( rij )
i =1 j > i
(6)
Um corpo em movimento pode diminuir a sua velocidade até atingir o repouso através
de fricção. Neste caso a energia cinética associada ao movimento orientado do corpo
converte-se na energia dos movimentos caóticos das moléculas dos corpos entre os
quais a fricção se realiza, isto é, em energia térmica. O aumento de energia térmica
resulta num aumento de temperatura do sistema. Dizemos, então, que há transferência
de energia, através de um processo que se designa por calor (ver figura 3.1).
Figura 3.1. Atrito e calor
Calor é mais outro conceito primitivo que intuitivamente está relacionado com as
sensações de quente e de frio. Sempre que exista uma diferença (gradiente) de
temperatura entre dois corpos em contacto, haverá uma tranferência de energia
térmica, através do processo designado por calor, do corpo a temperatura mais
elevada para o de temperatura mais baixa. A energia térmica deste aumenta assim
como a sua temperatura enquanto a energia térmica e temperatura do outro diminuem,
até que as temperaturas se igualem, ou seja, até que se atinja o equilíbrio térmico. Em
resumo, o processo-calor implica a existência de um gradiente de temperatura ao
passo que o processo-trabalho é caracterizado pela imposição de forças mecânicas
com orientação bem definida. Quando, a partir de agora, dissermos, de modo informal
e sucinto, que “um dado sistema absorveu calor” ou que “calor foi tranferido para um
sistema” ou outras expressões semelhantes, isso significa que há transferências de
energia por intermédio do processo-calor, mas não significa que o calor é uma forma
de energia.
Se o aumento de temperatura de um sistema for ∆T, a quantidade de energia, ∆Q,
transferida para o sistema através de calor, define-se como:
∆Q = c M ∆T
5
(7)
onde M é a massa e c é o calor específico, isto é, a quantidade de calor necessária
para aumentar de 1K a temperatura da unidade de massa do sistema. O calor
específico é uma propriedade característica de cada substância. Se o sistema for 1g
de água e se a sua temperatura aumentar de 1K, a quantidade de calor absorvida é, por
definição, 1cal (caloria). Assim, o calor específico da água é 1cal g-1 K-1. Se
exprimirmos a quantidade de substância em moles, o que é usual, c designa-se por
capacidade calorífica molar, a qual para a água tem o valor 18 cal mol-1 K-1. Se
utilizarmos estas unidades, então, na equação (7) em vez da massa M figurará o
número de moles.
O que dissémos anteriormente sobre fricção mostra que o trabalho pode produzir
calor (ou seja há transferências de energia por intermédio do processo-trabalho e do
processo-calor). Uma questão que surge imediatamente é saber que quantidade de
trabalho deve ser realizado para produzir 1cal de calor, ou seja, o equivalente
mecânico da caloria. Esse valor foi determinado, pela primeira vez , por James Joule
(1818-1889):
1 cal = 4.1840 J
(8)
Assim, a capacidade calorífica molar da água no sistema internacional é 75.3 J mol-1
K-1. Note-se, mais uma vez, que se utilizarmos a capacidade calorífica molar, em vez
do calor específico, a massa M na equação (7) deverá ser substituída pelo número de
moles.
A expressão (7) traduz quantitativamente a noção intuitiva de que a quantidade de
calor necessária para produzir uma variação de temperatura ∆T depende da massa
(quanto maior for a quantidade de uma dada substância mais calor será necessário
para produzir um dado ∆T), das propriedades da substância (as quantidades de calor
necessárias para produzir o mesmo ∆T em massas iguais de diferentes substâncias,
são diferentes) e, evidentemente, do valor de ∆T.
Adicionalmente, a expressão (7) é a equação fundamental da calorimetria, uma
técnica que permite determinar a quantidade de calor posto em jogo numa dada
transformação, a partir da medição da respectiva variação de temperatura e sabendo
antecipadamente os números de moles e as capacidades caloríficas molares das
substâncias envolvidas.
A expressão (7) mostra, também, que calor e temperatura são entidades diferentes o
que é importante sublinhar, uma vez que esses conceitos são frequentemente
confundidos. Mas, afinal, o que é temperatura? Para além da resposta trivial de que
temperatura é o que se mede com um termómetro, é conveniente analisarmos a
interpretação molecular da temperatura. Quando uma quantidade de calor é
6
transferida para um corpo parte da energia molecular caótica da fonte de calor passa
para o corpo por intermédio de colisões entre as moléculas. Essa energia molecular
não é mais do que energia cinética molecular numa forma desordenada (energia
térmica): as moléculas movem-se em todas as direcções e sentidos. Quando essa
energia é absorvida pelo sistema parte dela vai, em geral, aumentar a sua energia
térmica e a outra parte vai ser armazenada na forma de energia potencial
intermolecular (a qual depende, evidentemente, do tipo de moléculas) e,
eventualmente, na realização de trabalho: a expansão do sistema contra uma pressão
externa, por exemplo. Isto significa que, em geral, nem toda a energia térmica que saí
da fonte de calor aparece sob a forma de energia cinética molecular do corpo. Ora a
temperatura do corpo está somente relacionada com a sua energia cinética molecular
interna, mais precisamente com a energia cinética média das moléculas. De facto, a
teoria cinética mostra que a temperatura absoluta, T, é definida como:
N
T=
2 < ∑1/ 2mi vi2 >
i =1
3Nk B
(9)
onde N é o número de moléculas, kB é a constante de Boltzmann (1.381x10-23J.K-1) e
< > representa uma média, sobre o tempo, da energia cinética das N moléculas.
A expressão anterior mostra que a temperatura é uma intensidade energética: energia
cinética média por molécula.
A interpretação molecular da temperatura explica porque razão, em determinadas
circunstâncias, um sistema pode absorver calor sem experimentar uma variação da
sua temperatura como, por exemplo, durante as transições de fase sólido-líquido e
líquido-gás. Nesses casos, o calor absorvido não vai aumentar a energia cinética
molecular média, mas converte-se, totalmente, em energia potencial intermolecular
provocando um maior afastamento entre as moléculas (fusão dos sólidos e
vaporização dos líquidos).
Vimos que quando se realiza trabalho sobre um corpo de massa M ele pode aquirir
energia cinética sendo o movimento do corpo orientado segundo uma direcção bem
definida. Por outro lado, observámos que ao calor está associada, também, energia
cinética. Existe, no entanto, uma diferença fundamental : a energia cinética resultante
do trabalho é orientada, a do calor é desordenada, caótica, isto é, a qualidade da
energia num e noutro caso é diferente. Essa diferença tem uma consequência de
crucial importância: o calor transfere uma forma degradada de energia (energia
térmica). De facto, é possível transformar completamente uma dada quantidade de
trabalho em calor (por fricção, por exemplo), mas não é possível estabelecer um
7
processo cujo único resultado seja a conversão dessa quantidade de calor (energia
térmica) em trabalho. Esta impossibilidade que, como veremos, constitui a 2ª Lei da
Termodinâmica traduz afinal uma experiência diária: é muito fácil transformar um
sistema ordenado num sistema desordenado, mas o inverso não é verdadeiro.
Em resumo, trabalho e calor são processos (métodos) de transferência de energia. O
trabalho implica conexões mecânicas entre os sistemas e está relacionado com
movimentos orientados. O calor implica diferenças de temperatura e está relacionado
com movimentos moleculares desordenados (caóticos). Uma vez que um sistema
adquira uma dada quantidade de energia interna, não é possivel distinguir se essa
energia foi obtida através de calor ou de trabalho. De facto, a energia interna do
sistema é apenas a soma de energias cinética e potencial moleculares, nada mais. O
calor ou o trabalho só podem ser identificados se considerarmos o sistema mais
conexões com os seus arredores, isto é, se considerarmos os métodos de transferência
de energia.
2. Algumas Definições
Sistema é a parte do universo sob observação. O complementar do sistema no
universo designa-se por vizinhança, arredores ou exterior. A interface entre o sistema
e a vizinhança designa-se por parede. A união do sistema e da vizinhança constitui o
universo.
A definição exacta do sistema e das suas paredes é fundamental em Termodinâmica.
Assim, um sistema cujas paredes sejam impermeáveis ao calor (paredes adiabáticas),
inflexíveis (paredes rígidas) e impermeáveis à matéria (paredes fechadas) é um
sistema isolado, isto é, não interactua com a sua vizinhança. As transformações que o
sistema eventualmente sofra não têm qualquer interferência com o exterior. O
universo é, por definição, um sistema isolado.
Um sistema cujas paredes sejam permeáveis ao calor (paredes diatérmicas), rígidas e
fechadas é um sistema não isolado pois pode realizar trocas de calor com a sua
vizinhança. Se a rigidez das paredes for eliminada o sistema poderá, ainda, expandirse ou comprimir-se e, por conseguinte, trocar trabalho com o exterior.
Finalmente, se as paredes do sistema forem permeáveis à matéria (paredes abertas) o
sistema poderá trocar matéria com o exterior. Diz-se, por esse motivo, um sistema
aberto. A célula viva é um bom exemplo desse tipo de sistema. É evidente que as
transformações que um sistema pode realizar dependem directamente do tipo de
paredes.
Um sistema termodinâmico é caracterizado por propriedades específicas, designadas
por funções ou variáveis de estado, que podem ser medidas experimentalmente. O
8
volume, a temperatura, a pressão, a densidade, a composição química e a energia
interna são exemplos de funções de estado.
É importante sublinhar que as funções de estado só são precisamente definidas
quando o sistema se encontra em equilíbrio, ou seja, quando as propriedades do
sistema não variam no tempo e no espaço.
Consideremos, por exemplo, o sistema gasoso num cilindro provido de um êmbolo,
representado na figura 2.1. Quando o êmbolo está imóvel, fig. 2.1. a), o estado do gás
pode especificar-se indicando valores bem definidos para a sua pressão, temperatura e
densidade.
Figura 2.1. Estados de equilíbrio e não equilíbrio de um gás.
Se o gás for comprimido bruscamente, Figura 2.1.b), o seu estado, imediatamente
após a compressão, não pode descrever-se em termos de valores bem definidos para a
pressão, temperatura e densidade. De facto, o gás situado junto ao êmbolo está mais
comprimido (mais denso e com maior pressão interna) e quente do que o gás situado
no outro extremo do cilindro. Existem diferenças (gradientes) entre as temperatura,
pressão e densidade locais do gás. Trata-se de um estado de não-equilíbrio, porque
não sendo as suas propriedades espacialmente uniformes, a tendência espontânea do
sistema é eliminar, ao longo do tempo, os gradientes existentes, caminhando de modo
irreversível para um estado final de equilíbrio onde, então, as propriedades se
manterão constantes e uniformes. Irreversível, significa que o sistema por si só, isto é,
espontâneamente, não voltará ao estado de não-equilíbrio. Vamos estudar apenas os
estados de equilíbrio e as variações sofridas pelas funções de estado quando um
sistema passa dum estado de equilíbrio para um outro estado de equilíbrio. Este
estudo baseia-se numa propriedade muito importante das funções de estado: a sua
9
variação não depende do processo (ou caminho) pelo qual se realiza uma
transformação, mas apenas do estado inicial e do estado final.
B
1
2
A
Figura 2.2. Transformação do estado A para o estado B realizada por dois processos
diferentes.
Consideremos a Figura 2.2. e suponhamos que o estado A representa a Universidade
de Lisboa caracterizada pela sua altitude hA, em relação ao nível do mar, e o estado B
representa o Cristo-Rei caracterizada pela sua altitude hB, em relação ao mesmo nível.
Se nos deslocarmos de A para B podemos seguir caminhos diferentes. Por exemplo,
podemos sair da Universidade e atravessar a ponte Vasco da Gama até chegar ao
Cristo-Rei (caminho 1) ou ir através da ponte 25 de Abril (caminho 2). É evidente que
qualquer que seja o caminho seguido, a diferença de altitudes entre A e B, isto é, a
variação de altitude que sofremos através da nossa viagem é independente do
caminho seguido:
(10)
hB – hA (caminho 1) = hB – hA (caminho 2) = ∆h
A altitude é, assim, uma função de estado. No entanto, propriedades como a distância
percorrida, o trabalho realizado e o calor dispendido não são funções de estado pois
dependem, evidentemente, do caminho escolhido.
Suponhamos, agora, a seguinte reacção de oxi-redução:
Zn ( s ) + Cu 2+ ( aq ) → Zn 2+ ( aq ) + Cu ( s )
(11)
Designaremos o estado inicial, constituído pelos reagentes, por A e o estado final,
constituído pelos produtos, por B. Tanto o estado inicial como o final estão bem
definidos pelas suas funções de estado, nomeadamente, temperatura, pressão,
composição química e energia interna. A reacção anterior pode ser realizada por dois
processos completamente diferentes. Um dos processos, que designaremos por 1, pela
mistura directa dos reagentes. O outro processo, que designaremos por 2, com os
reagentes separados no espaço e constituindo uma pilha electroquímica. Suponhamos
que ambos os processos se realizam a temperatura e pressão constantes o que é fácil
10
de executar experimentalmente uma vez que se disponha dum termostato e que as
reacções se realizem, por exemplo, em recipientes abertos (pressão atmosférica).
Os processos considerados constituem, assim, uma tranformação do estado A para o
estado B, realizada por dois caminhos diferentes. Se partimos das mesmas condições
iniciais e chegamos às mesmas condições finais as variações das propriedes de estado
(que por definição o caracterizam) devem ser iguais para os dois processos. Assim,
teremos para a energia interna:
E B − E A ( processo 1) = E B − E A ( processo 2 ) = ∆E
(12)
Se designarmos a composição química, de um modo geral, por CQ:
CQ B − CQ A ( processo 1) = CQ B − CQ A ( processo 2 ) = ∆CQ
(13)
Dado que a transformação se realiza a temperatura e pressão constantes, teremos:
TB − TA ( processo 1) = TB − TA ( processo 2 ) = ∆T = 0
p B − p A ( processo 1) = p B − p A ( processo 2 ) = ∆p = 0
(14)
Contudo, tal como nas opções para atingir o Cristo-Rei, o calor e o trabalho postos em
jogo nos dois processos não são iguais. De facto, a experiência mostra que quando a
reacção é realizada pela mistura directa dos reagentes (processo 1) a quantidade de
calor libertada 216 kJ.mol-1. Neste caso não é realizado trabalho eléctrico. Quando a
reacção é realizada numa pilha electroquímica (processo 2) pode realizar-se trabalho
eléctrico com um valor máximo de 212 kJ.mol-1 e, neste caso, o calor libertado será
apenas de 4 kJ.mol-1.
Em resumo, existem grandezas físicas, designadas por funções ou variáveis de estado,
que caracterizam o estado de um sistema em equilíbrio e cujas variações não
dependem dos caminhos pelos quais os sistemas realizem transformações: energia
interna, composição química, temperatura, pressão, etc. Por outro lado, existem
grandezas físicas, tais como o calor e o trabalho, cujas quantidades dependem dos
caminhos pelos quais os sistemas realizem transformações. Tais grandezas, como é
evidente, não podem caracterizar o estado de um sistema. Esta a razão porque
dizemos, por exemplo, que o sistema A tem a energia interna EA, a temperatura TA e a
pressão pA, mas nunca dizemos que o mesmo sistema tem, como propriedade, o calor
QA ou o trabalho WA.
11
É importante distinguir dois tipos de funções de estado: intensivas e extensivas.
Observemos a figura seguinte:
a
d
c
b
e
f
g
h
Figura 2.3. O todo nem sempre é igual à soma das partes!
Suponhamos que o rectângulo representa um sistema num estado de equilíbrio e que
a, b, c, ... são subsistemas obtidos por uma partição arbitrária. O sistema é
caracterizado por um determinado número de moléculas ou massa, energia interna,
volume, temperatura, pressão , densidade, etc. A massa, volume e energia do sistema
são iguais à soma das massas, volumes e energias de cada um dos subsistemas, pois
tratam-se, claramente, de propriedades directamente proporcionais ao número de
moléculas. No entanto, a temperatura, pressão e densidade do sistema são iguais,
respectivamente, à temperatura, pressão e densidade de cada um dos subsistemas,
pois tratam-se de propriedades independentes do número de moléculas. De facto,
vimos que a temperatura não é mais do que uma intensidade energética: energia
térmica média por molécula. Analogamente, a pressão é, também, uma intensidade:
número médio de colisões por unidade de área e de tempo. Assim é, também, a
densidade: número médio de moléculas (ou massa) por unidade de volume. Como a
legenda da Figura 2.3 exprime: o todo nem sempre é igual à soma das partes. Isto é, a
temperatura do sistema, por exemplo, não é igual à soma das temperaturas dos
subsistemas.
As propriedades que são directamente proporcionais ao número de moléculas (ou, o
que é equivalente, à massa) como o volume, energia interna e a própria massa,
designam-se por variáveis extensivas. As propriedades que são independentes do
número de moléculas, ou da massa, como a temperatura, pressão e densidade,
designam-se por propriedades intensivas.
Finalmente, um dos objectivos da Termodinâmica é estabelecer relações entre as
funções de estado dos sistemas em equilíbrio. Um exemplo dessas relações é a
equação de estado dos gases perfeitos:
pV = n R T
onde n é o número de moles e R é a constante dos gases (8.314 J.mol-1.K-1).
12
(15)
Note-se que basta conhecerem-se, apenas, duas variáveis de estado, para que a outra
fique determinada através da equação anterior. Assim, se medirmos o volume e a
temperatura das n moles do gás a sua pressão será:
p=nRT/V
(16)
Se, pelo contrário, medirmos a pressão e a temperatura o volume será:
V=nRT/p
(17)
e, assim, sucessivamente.
Isto significa que o gás em equilíbrio fica inteiramente definido, apenas, por duas
variáveis de estado. Trata-se, afinal, duma característica fundamental da
Termodinâmica: o número de variáveis de estado independentes para definir o estado
termodinâmico de um sistema em equilíbrio é muito pequeno quando comparado com
o número de moléculas que o constituem. Na realidade, n moles de um gás contêm um
número de moléculas da ordem de n.1023. As moléculas encontram-se em movimento
e colisões incessantes e se pretendermos seguir a sua dinâmica teremos de definir,
pelo menos, 6.n.1023 variáveis: 3 coordenadas para a posição e 3 coordenadas para a
velocidade de cada molécula.
Um estado dinâmico do sistema definido deste modo designa-se por microestado. É
claro que o microestado do sistema varia ao longo do tempo, a despeito das
propriedades termodinâmicas, medidas experimentalmente, se manterem constantes
num estado de equilíbrio. Este facto, reflecte um dos aspectos mais apaixonantes da
Natureza: as propriedades que caracterizam um estado de equilíbrio de um sistema,
medidas experimentalmente, não são mais do que valores médios das propriedades
dos microestados que o sistema realiza ao longo do tempo. Existe, assim, uma
infinidade de microestados, a nível molecular, compatível com um dado estado
termodinâmico de equilíbrio onde as propriedades macroscópicas se mantêm
constantes.
3. A 1ª Lei da Termodinâmica
Já vimos que a energia é uma propriedade que se conserva ao longo dos processos.
Pode ser transferida de um sistema para outro, através de calor e/ou de trabalho, e
convertida em diferentes tipos, mas nunca pode ser criada a partir do nada, nem
destruida. Estes factos, confirmados pela experiência diária, são traduzidos pela 1ª Lei
da Termodinâmica, a qual pode ser enunciada do seguinte modo: a energia do
universo é constante. Tratando-se de uma lei de conservação, ela ensina-nos a fazer o
13
balanço correcto das transferências de energia entre um dado sistema e a sua
vizinhança.
Por exemplo, se um sistema absorver uma quantidade de energia, ∆Q, através do
processo-calor e sobre o sistema for realizada uma quantidade de trabalho ∆W, então
a variação da energia interna do sistema, ∆E, é:
∆E = ∆Q + ∆W
(18)
A equação anterior traduz, claramente, que a energia se conserva e é a expressão
matemática da 1ª Lei da Termodinâmica: a energia transferida para o sistema pelos
dois processos (calor e trabalho) é totalmente contabilizada e vai contribuir para o
aumento da energia interna do sistema. Note-se que ∆Q e ∆W são fornecidos pela
vizinhança, portanto, a energia do universo mantem-se constante.
É importante introduzir a convenção de sinais relativamente ao calor e ao trabalho.
Assim :
Se o sistema absorver calor
∆Q > 0
Processo endotérmico
Se o sistema libertar calor
∆Q < 0
Processo exotérmico
Se o sistema receber trabalho
∆W > 0
Se o sistema realizar trabalho
∆W < 0
Reescrevendo, por exemplo, a equação (18) como:
∆Q = ∆E - ∆W
(19)
é evidente que a quantidade de calor só será totalmente armazenada como energia
interna se o sistema não receber ou realizar trabalho, isto é, se ∆W = 0. Se o sistema
realizar trabalho sobre o exterior, então, uma parte da energia absorvida vai ser
utilizado na produção desse trabalho e a outra parte contribuirá para a energia interna.
Um tipo de trabalho importante é o de pressão-volume (também designado por
trabalho de expansão-compressão), ou seja, o trabalho contra uma força externa que
actue sobre o sistema, resultando numa expansão ou compressão. Se a força externa,
f ex , for constante o trabalho realizado será:
∆W = −f ex .∆r
(20)
onde o sinal negativo significa que a força exercida pelo sistema tem sinal contrário
ao da força externa.
14
A expressão anterior pode ser reescrita em termos de propriedades de estado o que é,
obviamente, mais conveniente sob o ponto de vista termodinâmico. Introduzindo a
área, A, da superfície do sistema, no segundo membro da expressão (20), teremos:
∆W = −
f ex
A ∆r = − pex ∆V
A
(21)
onde p ex é a pressão exercida sobre o sistema e ∆V é a variação do seu volume.
Se a pressão interna, p in , for maior do que a pressão externa, p ex , então o sistema
realizará uma expansão: ∆V>0 e ∆W < 0, isto é, o sistema realiza trabalho sobre o
exterior. Se, pelo contrário, p in < p ex , então o sistema sofre uma compressão: ∆V<0 e
∆W> 0, ou seja, o sistema recebe trabalho do exterior. Finalmente, se p in = p ex , o
sistema estará em equilíbrio.
Note-se que na expressão (21) considerámos a pressão constante. Dum modo geral, a
pressão varia com o volume e, assim, a expressão geral para o trabalho de pressãovolume é:
V2
∆W = − ∫ pex dV
V1
(22)
É claro que para calcular o integral anterior teremos de saber como a pressão varia
com o volume. Se o sistema for um gás perfeito, por exemplo, essa variação é
expressa pela equação de estado (16).
4. Entalpia
Sabemos que a energia interna dum sistema é uma função de estado, isto é, a sua
variação não depende do caminho pelo qual o sistema realize uma dada
transformação. No entanto, como vimos, o calor e o trabalho dependem do caminho.
Consideremos, uma reacção química qualquer:
A+B→C+D
(23)
A variação da energia interna do sistema é:
∆E = ( E C + E D ) − ( E A + E B )
15
(24)
Suponhamos que a reacção é endotérmica, isto é, absorve energia através de calor, ∆Q
> 0. De acordo com a expressão da 1ª Lei (19): ∆E = ∆Q + ∆W.
Se reacção for realizada a volume constante a variação do volume será nula e de
acordo com (21), o trabalho de pressão-volume também será nulo. Então, se não
houver a realização de outro tipo de trabalho (por exemplo, trabalho eléctrico)
teremos:
∆E = ( ∆Q ) V
(25)
isto é, todo o calor é armazenado como energia interna. Isto significa que, neste caso,
para determinar a variação da energia interna da reacção basta medir o calor posto em
jogo num calorímetro a volume constante.
Suponhamos, agora, que a mesma reacção é realizada a pressão constante. Então, de
acordo com (21) o trabalho de pressão-volume será ∆W = - p∆V. Se não houver a
realização de outro tipo de trabalho, teremos, de acordo com a 1ª Lei:
∆E = ( ∆Q ) p − p∆V
(26)
Uma vez que ∆E é igual nos dois casos, pois a energia interna é uma função de
estado, é evidente que ( ∆Q ) p ≠ ( ∆Q ) V , ou seja, o calor posto em jogo, neste caso, já
não é igual à variação da energia interna do sistema.
Podemos definir, no entanto, uma outra função de estado, cuja variação é igual ao
calor posto em jogo na reacção em condições de pressão constante. Essa função
designa-se por entalpia, H, e define-se como:
H = E + pV
(27)
Dado que a energia interna, pressão e volume são funções de estado, é evidente que a
entalpia também é uma função de estado. Para uma transformação a pressão
constante, teremos:
∆H = ∆E + p∆V
(28)
Para a mesma transformação, e supondo que apenas é realizado trabalho de pressãovolume, ∆E é dado pela expressão (26). Introduzindo essa expressão na equação (28)
obtem-se:
∆H = ( ∆Q ) p
16
(29)
Isto significa que a variação de entalpia duma reacção química pode ser determinada
medindo o calor posto em jogo na reacção num calorímetro a pressão constante.
Em resumo, numa reacção química em que o único trabalho realizado seja trabalho
de pressão-volume, o calor posto em jogo na reacção é igual:
a) à variação da energia interna se a reacção for realizada em condições de volume
constante.
b) à variação de entalpia se a reacção for realizada em condições de pressão
constante.
Suponhamos que a mesma reacção se realiza a pressão constante, mas com produção
de trabalho eléctrico numa pilha electroquímica. Neste caso, é fácil estabelecer que:
∆H = (∆Q)elp − ∆Wel
(30)
Como ∆H é a mesma nos dois casos, então ( Q )p é diferente de ( ∆Q ) p da expressão
el
(29). Se ∆H >0 e se o sistema realizar trabalho eléctrico, a quantidade de calor
absorvido terá de ser maior do que se não realizasse esse trabalho, uma vez que ∆H
será o mesmo para ambos os processos. Se ∆H <0 o calor libertado será menor do que
se não realizasse trabalho eléctrico, como vimos para a reacção (11).
A partir da expressão (27) e de um modo geral:
∆H = ∆E + ∆ ( pV ) = ∆E + ( p 2 V2 − p 1 V1 )
(31)
em que 1 e 2 designam, respectivamente, o estados inicial e final do sistema. A
diferença entre ∆E e ∆H depende, assim, do valor da variação de pV para os estados
inicial e final. No caso de reacções químicas, a pressão constante, em que
intervenham somente sólidos e líquidos p 1 V1 ≅ p 2 V2 e, como tal, ∆E e ∆H são
aproximadamente iguais. No entanto, no caso de reacções gasosas, essa diferença
pode ser apreciável.
Consideremos uma reacção qualquer onde somente intervenham gases e suponhamos
que a reacção se realiza a temperatura, T, constante:
aA ( g ) + bB( g ) → cC ( g ) + dD( g )
(32)
De acordo com a lei de Dalton das pressões parciais:
pV (produtos) = (c + d) RT
17
(33)
e
pV (reagentes) = (a + b) RT
(34)
∆(pV) = [(c + d) - (a + b) ] RT = ∆n RT
(35)
donde:
onde ∆n representa a diferença entre o número de moles dos produtos e reagentes.
Finalmente:
∆H = ∆E + ∆n RT
(36)
A expressão anterior foi deduzida com base na equação dos gases perfeitos (15) e, por
conseguinte, é uma relação aproximada. No entanto, a maioria dos gases reais, a
pressões e densidades suficientemente baixas, são descritos, com boa aproximação,
por essa equação. Assim, a equação anterior dá-nos, pelo menos, uma ordem de
grandeza da diferença entre ∆H e ∆E para reacções químicas em fase gasosa.
5. Cálculos Entálpicos
O calor posto em jogo numa reacção química está relacionado, como vimos, com a
variação de energia envolvida na passagem dos reagentes aos produtos. É importante
determinar a energia absorvida ou libertada pelas reacções químicas e, de acordo com
a 1ª Lei da Termodinâmica, analisar como essa energia pode ser utilizada.
Os cálculos energéticos relativamente aos processos de combustão, por exemplo, são
de importância fundamental para decidir se o carvão, ou o gás natural, é o
combustível mais económico para um determinado objectivo, ou se as batatas
engordam mais do que o bife. A base desses cálculos, aparentemente tão desconexos,
é, no entanto, a mesma: a 1ª Lei.
Consideremos a seguinte reacção realizada à temperatura constante de 298 K (25 ºC)
e à pressão constante de 1 bar (105 Pa):
C ( grafite ) + O 2 ( g ) → CO 2 ( g )
(37)
O calor posto em jogo nesta reacção pode ser medido directamente num calorimetro
obtendo-se 393.5 kJ. Como a reacção é exotérmica, e se realiza em condições de
pressão constante, podemos estabelecer que ∆H = -393.5 kJ, tendo em conta o que
18
dissémos sobre processos que se realizem a pressão constante e sobre convenções de
sinais.
Se, nas mesmas condições experimentais, pretendermos determinar o calor posto em
jogo na seguinte reacção:
1
C ( grafite ) + O 2 ( g ) → CO( g )
2
(38)
deparamos com uma enorme dificuldade: formam-se, simultaneamente, quantidades
apreciáveis de CO2. A formação deste subproduto é acompanhada de libertação de
calor como vimos acima, o que torna impossível medir directamente o calor referente,
exclusivamente, ao monóxido de carbono.
Todavia, podemos estabelecer o ciclo de reacções representado na figura seguinte. A
cada um dos passos está associado um valor de ∆H e como a entalpia é uma função de
estado:
∆H1 = ∆H2 + ∆H3
(39)
onde, como vimos, ∆H1 = -393.5 kJ.
A reacção correspondente ao passo 3 pode ser, também, facilmente realizada num
calorimetro sem a interferência de reacções pararalelas, uma vez que se disponha de
CO e O2, sendo ∆H3 = -283.0 kJ. Então, a partir de (39) teremos:
∆H2 = ∆H1 - ∆H3 = -110.5 kJ
(40)
Consideremos as reacções correspondentes a ∆H1 e ∆H3, respectivamente:
C ( grafite ) + O 2 ( g ) → CO 2 ( g ) ⇒ ∆H 1
19
(41)
e
1
CO ( g ) + O 2 ( g ) → CO 2 ( g ) ⇒ ∆H 3
2
(42)
Se, por analogia com (40) subtrairmos, membro a membro, a equação (42) da equação
(41) obtemos:
1
C ( grafite ) + O 2 ( g ) → CO ( g ) ⇒ ∆H 2 = ∆H 1 − ∆H 3
2
(43)
isto é, a equação correspondente ao passo 2.
As equações químicas podem, assim, ser formalmente tratadas como equações
matemáticas no que diz respeito aos cálculos entálpicos.
Vejamos o exemplo seguinte:
Exemplo 1: Calcular o valor de ∆H para a reacção:
C(grafite) + H2O(g) → H2(g) + CO(g)
a partir das variações de entalpia para as reacções:
C(grafite) + 1/2 O2(g) → CO(g)
∆H = -110.5 kJ
H2(g) + 1/2 O2(g) → H2O(g)
∆H = -241.8 kJ
Subtraindo, membro a membro, a segunda equação da primeira, obtemos:
C(grafite) + H2O(g) → H2(g) + CO(g)
∆H = -110.5 -(-241.8) = +131.3 kJ
A equação (39) traduz a Lei de Hess: a variação de entalpia de uma reacção química
é independente do número de etapas ou do processo pelo qual se realiza a reacção. A
sua validade reside no facto de a entalpia ser uma função de estado e a sua
importância é evidente: permite o cálculo das entalpias de reacções cuja determinação
experimental seja difícil ou impossível.
20
6. Entalpias Padrão
Consideremos uma reacção química qualquer:
aA + bB → cC + dD
A variação de entalpia será:
∆H = (cHC + dDD) - (aHA+ bHB)
onde Hi ( i = A,B,C,D ) são as entalpias molares absolutas dos reagentes e produtos.
Dum modo geral:
∆H = ∑ n H(produtos) − ∑ n H(reagentes)
(44)
onde n designa os coeficientes estiquiométricos.
Se tivessemos uma tabela com os valores das entalpias absolutas para todas as
substâncias conhecidas, poderiamos, a partir da equação anterior, calcular ∆H para
qualquer reacção.
Sob o ponto de vista experimental, no entanto, é impossível determinar entalpias
absolutas. Apenas se podem medir diferenças de entalpias através do calor posto em
jogo nas reacções. Mas é precisamente na diferença de entalpia, ∆H, que estamos
interessados. Para resolver o problema pensemos por analogia com o exemplo
seguinte. Consideremos as montanhas da figura Figura 6.1.
hM
B
A
hA1
hB1
Superfície do Mar
hF
hA2
hB2
Fundo do Mar
21
Figura 6.1. As altitudes dependem do estado de referência, mas as suas diferenças
não.
Quais as altitudes das montanhas? Evidentemente que dependem do estado de
referência. Se escolhermos a superfície do mar com estado de referência, atribuindolhe a altitude zero, então as altitudes das montanhas serão +hA1 e +hB1 e a “altitude”
do fundo do mar -hF. Mas se escolhermos o fundo do mar como referência,
atribuindo-lhe a altitude zero, então as altitudes das montanhas serão diferentes: +hA2
e +hB2 e a altitude da superfície do mar +hF. Repare-se, no entanto, que a diferença
de altitudes das montanhas, ∆h, é independente do estado de referência escolhido, isto
é:
∆h = hB1 - hA1 = hB2 - hA2 = hM
Assim como a diferença de altitudes da superficie e do fundo do mar:
∆h = 0 - (-hF) = hF - 0 = hF
Isto significa que podemos constituir uma tabela com as altitudes das diferentes
montanhas e vales convencionando um estado de referência qualquer a que
atribuimos o valor zero. A partir dessa tabela podemos calcular as diferenças de
altitudes de quaisquer duas montanhas ou vales. Essas diferenças são invariantes.
Um raciocínio análogo pode ser aplicado ao problema das entalpias. Define-se o
estado normal de cada elemento ou composto como a sua forma física mais estável à
pressão de 1 bar (105 Pa) e a uma temperatura especificada, geralmente 298 K (25ºC).
Por convenção atribui-se a cada elemento, no seu estado normal, a entalpia zero.
Estabelece-se, assim, um estado de referência ou estado padrão para as entalpias.
A variação de entalpia que acompanha a formação de 1 mole de um composto no
estado normal a partir dos seus elementos no estado normal, chama-se entalpia
padrão de formação e designa-se por ∆H of .
Por exemplo:
C(grafite,1bar,298K) + O2(g,1bar,298K) → CO2(g,1bar,298K)
∆H = ∆H of (CO2) = -393.5 kJ.mol-1
H2(g,1bar,298K) + 1/2 O2(g,1bar,298K) → H2O(g,1bar,298K)
∆H = ∆H of (H2O,g) = -241.8 kJ.mol-1
22
Dispondo de uma tabela com as entalpias padrão de formação para as diferentes
substâncias (ver bibliografia indicada) a variação de entalpia padrão, ∆Ho, para uma
dada reacção será:
∆H o = ∑ n ∆H fo (produtos) − ∑ n ∆H of (reagentes)
(45)
onde o símbolo º designa as condições físicas padrão em que se processa a reacção:
temperatura de 298K e pressão de 1bar. Se as condições forem diferentes, o valor de
∆H para a reacção será, em geral, diferente de ∆Ho. Teremos de saber, então, como
calcular ∆H a partir de ∆Ho. Veremos mais tarde essa relação.
Consideremos o exemplo seguinte:
Exemplo 2: A partir de uma tabela de entalpias padrão calcular a variação de entalpia
padrão da combustão do amoníaco para formar vapor de água e i) azoto ii) monóxido
de azoto.
Para o caso i):
2NH3(g) + 3/2 O2(g) → N2(g) + 3H2O(g)
o
∆H = [ ∆H of (N2) +3 ∆H of (H2O)] - [2 ∆H of (NH3)+3/2 ∆H of (O2)] =
= 0 + 3(-241.8) - 2(-46.2) - 3/2(0)
donde:
∆Ho = -632.99 kJ
Para o caso ii):
2NH3(g) + 5/2 O2(g) → 2NO(g) + 3H2O(g)
o
∆H = [2 ∆H of (NO) +3 ∆H of (H2O)] - [2 ∆H of (NH3)+5/2 ∆H of (O2)]
= 2(+90.4) + 3(-241.8) - 2(-46.2) - 5/2(0)
donde:
∆Ho = -456.4 kJ
As tabela de entalpias padrão contêm, também, valores para entalpias de átomos e de
iões. É importante ver como elas foram estabelecidas em relação ao estado padrão de
entalpia zero: os elementos químicos no seu estado normal.
A existência de átomos livres em sistemas químicos é, em geral, transitória. O átomo
de hidrogénio, por exemplo, apenas existe em pequenas concentrações nas chamas,
explosões e outros sistemas reaccionais em que intervenham compostos que
contenham hidrogénio. O valor de ∆H of para o átomo de hidrogénio é definido como
metade da energia necessária para romper as ligações de 1 mol de moléculas de
hidrogénio, ou seja, metade da energia de dissociação do hidrogénio:
23
H2 → 2 H
∆H = 2∆H (H) - ∆H of (H2) = 2∆H of (H) = 436 kJ
o
o
f
donde
∆H of (H) = 218 kJ.mol-1
As entalpias de formação de outros átomos são calculadas de modo semelhante, com
base nas energias de dissociação das respectivas moléculas.
As entalpias de formação de átomos correspondentes a elementos sólidos obtêm-se
medindo ∆Ho para o processo de vaporização. Assim, por exemplo, o estado normal
do carbono é o cristal de grafite a 298 K e pressão de 1bar para o qual a entalpia é
zero. O calor absorvido quando se vaporiza 1 mole de grafite para formar 1mole de
átomos gasosos é a entalpia de sublimação do carbono:
C(grafite) → C(átomos gasosos)
∆H = ∆H (C,átomo) - ∆H of (C,grafite) = 716.7 kJ mol-1 (entalpia de sublimação)
∆Ho = ∆H of (C,átomo) = 716.7 kJ mol-1
o
o
f
Em muitas reacções em fase líquida, particularmente em solução aquosa, intervêm
iões. Estudámos, por exemplo, as reacções ácido-base onde existe uma reacção iónica
comum:
H+(aq) + OH-(aq) → H2O(liq)
Dada a importância das reacções iónicas é necessário estabelecer os valores de ∆H of
para iões individuais como, por exemplo, H+ e OH-.
Consideremos a formação de uma solução 1M de ácido clorídrico a partir de cloro e
hidrogénio nos seus estados normais:
1/2 H2(g) + 1/2 Cl2(g) → HCl (g)
∆Ho = ∆H of (HCl) = -92,5 kJ.mol-1
HCl(g) + n H2O(liq) → H+(aq) + Cl-(aq)
∆Ho = -74.9 kJ
onde nH2O representa a quantidade de água necessária para produzir uma solução
1M. Somando membro a membro as equações anteriores, obtem-se:
1/2 H2(g) + 1/2 Cl2(g) → H+(aq) + Cl-(aq)
∆Ho = -167.4 kJ
É evidente que -167.4 kJ é a soma das entalpias de formação de H+(aq) e Cl-(aq).
Dado que as soluções iónicas são sempre neutras, não é possível individualizar,
24
experimentalmente, as entalpias de formação do ião positivo e do negativo. No
entanto, convenciona-se, que ∆H of (H+) = 0 donde ∆H of (Cl-) = -167.4 kJ.mol-1.
Com base na convenção anterior é fácil estabelecer as entalpias para outros iões.
Consideremos o seguinte:
Exemplo3: Quando 1mol de ácido forte se neutraliza com uma base forte ∆Ho = -57.3
kJ. A entalpia padrão de formação da água líquida é -285.8 kJ.mol-1. Calcular a
entalpia de formação de OH-.
As reacções a considerar são:
H+(aq) + OH-(aq) → H2O(liq)
∆Ho = -57.3 kJ
H2(g) + 1/2 O2(g) → H2O(liq)
∆Ho = -285.8 kJ
Subtraindo a primeira equação da segunda:
H2(g) + 1/2 O2(g) → H+(aq) + OH-(aq)
∆Ho = -228.5 kJ
Considerando as convenções estabelecidas anteriormente:
∆Ho = ∆H of (OH-) = -228.5 kJ mol-1
7. Energia de Ligações Químicas
A partir das entalpias de reacções apropriadamente escolhidas é possível estimar as
energias médias de ligações químicas. Trata-se de um aspecto muito importante sob o
ponto de vista teórico e experimental.
Considere-se o metano:
e a reacção da sua decomposição (dissociação) completa:
CH4 (g) → C (g) + 4H(g)
∆Ho = 1665 kJ mol-1
Nesta reacção são dissociadas 4 ligações químicas C-H. Assim, a energia média que é
necessário fornecer ao metano para dissociar 1mol dessas ligações é 1665 / 4 = 416 kJ
mol-1. Este será, por sua vez, o calor libertado quando 1 mol de ligações C-H se
formarem no metano.
25
As energias de dissociação para as ligações C-H, que designaremos dum modo geral
por D(C-H), existentes em diferentes compostos não são exactamente iguais à do
metano, pois as respectivas estruturas moleculares diferem. Contudo, a experiência
mostra que os valores são suficientemente próximos para se estabelecerem tabelas
com energias médias de diferentes ligações, calculadas sobre uma vasta selecção de
compostos que contenham uma dada ligação (ver tabela 7.1).
Tabela 7.1- Energias médias de ligação (298K)
Ligação
Energia de Ligação
kJ mol-1
Ligação
Energia de Ligação
kJ mol-1
H2
436
F2
153
C-H
413
H-F
565
C-C
348
H-Cl
431
C=C
614
H-Br
366
C≡C
839
H-I
297
C-Cl
339
C-F
485
C=O
745
P-H
322
C≡N
891
H-N
391
C-O
358
H-S
277
O-H
462
N=O
628
O-O
146
S=O
435
O-N
209
N-N
268
O-Cl
205
C-Br
285
Note-se que enquanto D(C-H) = 416 kJ mol-1 para o metano, o valor tabelado é de
413. Este é o valor médio obtido sobre um vasto número de compostos contendo a
ligação C-H.
***********************************
Problemas Propostos
1. Detemine D(C-C) para o etano:
considerando os valores médios de D(C-H) e D(H2) na tabela 7.1, e sabendo que
∆H of (C2H6) = -83 kJ mol-1 e D(grafite) = 717 kJ mol-1. Compare com o valor médio
de D(C-C) tabelado.
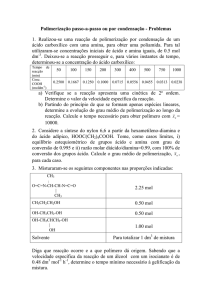
2. Considere os compostos representados pelas seguintes estruturas simplificadas:
26
;
H-C ≡ C-H
a) Identifique os compostos.
b) Estime as respectivas energias D(C=C) e D(C≡C) considerando os valores
médios de D(C-H) e D(H2) da tabela 7.1, e sabendo que ∆H of (C2H4) = 52,26
kJ mol-1 e ∆H of (C2H2) = 226,73 kJ mol-1. Compare os valores obtidos com os
da tabela.
3. a) Identifique os seguintes compostos
c) Estime as energias D(C=O) para os dois compostos, considerando as energias
médias D(C-H), D(C-O), D(O-H) e D(H2) tabeladas, e sabendo que
∆H of (CH3COCH3 (g)) = -218,5 kJmol-1 e ∆H of (CH3COOH (g)) = -438,1
kJmol-1. Compare os resultados obtidos com o da tabela.
4. Considere a seguinte reacção de hidogenação em fase gasosa:
Recorrendo à tabela 7.1, estime a entalpia padrão da reacção, ∆Ho. A reacção será
exotérmica ou endotérmica? (Sugestão: calcule as energias de dissociação totais para
o eteno e hidrogénio, e a energia total da formação das ligações do etano).
5. Questão análoga à anterior para a reacção:
3CH4 (g) → C3H8 (g) + H2 (g)
6. a) A variação de entalpia experimental para a reacção de atomização do
benzeno:
27
traduzida pela equação:
C6H6 (g) → 6C (g) + 6H (g)
é
∆Ho = 5535 kJ
Estime o valor da entalpia da reacção com base na tabela 7.1 e na fórmula de
estrutura acima.
b) Compare o valor estimado com o experimental e interprete o resultado com
base nas estruturas de ressonância do benzeno, por exemplo,
e na deslocalização das orbitais moleculares π:
(Sugestão: faça uma revisão do estudo sobre a estrutura molecular)
Nota Final
Este texto de apoio destina-se a complementar algumas aulas teóricas, mas não
dispensa a consulta da bibliografia recomendada. Agradeço aos leitores que me
indiquem possíveis erros ou afirmações que considerem pouco claras.
28