Complementos de Física – Exercícios Teoria

Universidade Paulista – UNIP
Curso: Engenharia/Básico
Disciplina: Complementos de Física – Teoria
prof. Gilberto Lima
Exercícios Propostos da Apostila – págs. 135 a 142
Resoluções
1) a) No instante to = 0 s, a barra ℓ é abandonada sobre os trilhos o que promove o fechamento
do circuito e o estabelecimento de uma corrente io no sentido horário produzida pelo gerador




com fem ε. Nesse instante, usando a Lei das Malhas de Kirchhoff   Vi  0  , teríamos a
i
seguinte equação para descrever o circuito (lembrando que há uma resistência global R nessa
malha, conforme dito no enunciado):
 Vi  0
  Rio  0

i

  Rio

io 

R

Mas ocorre uma interação entre esta corrente io e o campo magnético externo B , e, portanto,
surge uma força magnética sobre a barra, cujo valor é dado por:

Fmagnética  io Bsen


Fmagnética  Bsen90 o
R




Fmagnética  B,
R
onde β é o ângulo entre o campo magnético e a corrente; neste caso β = 90o.
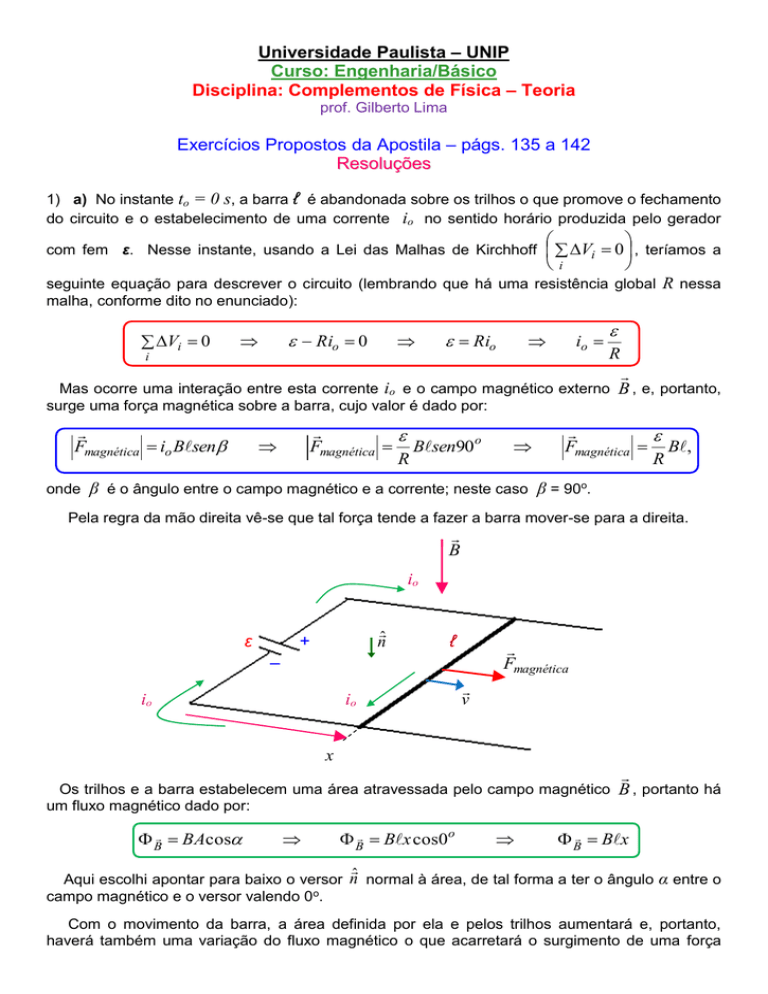
Pela regra da mão direita vê-se que tal força tende a fazer a barra mover-se para a direita.

B
io
ε

n̂
+
ℓ

Fmagnética
–
io
io

v
x

Os trilhos e a barra estabelecem uma área atravessada pelo campo magnético B , portanto há
um fluxo magnético dado por:
 B  BAcos

 B  Bx cos0o

 B  Bx

Aqui escolhi apontar para baixo o versor n̂ normal à área, de tal forma a ter o ângulo α entre o
campo magnético e o versor valendo 0o.
Com o movimento da barra, a área definida por ela e pelos trilhos aumentará e, portanto,
haverá também uma variação do fluxo magnético o que acarretará o surgimento de uma força
eletromotriz induzida (εinduzida) e também de uma corrente induzida (iinduzida).
dados pela lei de Faraday-Lenz e depois pela lei de Ohm:
 induzida  

d B
dt
 induzida   B

 induzida  
dx
dt

Seus valores são
d [ Bx]
dt
 induzida   Bv
onde v é a velocidade de deslocamento da barra.
iinduzida 
E:
 induzida

R
iinduzida 
 Bv
R

A função destas duas grandezas é produzir um campo magnético induzido ( Binduzido ) que se
contraponha à variação do fluxo; no caso, como o fluxo está aumentando juntamente com a área
delimitada pela barra, a fem e a corrente induzidas se estabelecem no sentido anti-horário, de
forma a produzirem um campo magnético induzido com sentido para cima (regra da mão direita),
para tentar compensar o aumento do fluxo magnético
para baixo. Esta corrente induzida também

interagirá
com o campo magnético externo B , o que produzirá uma força magnética induzida

( Fmag .induzida ) que aponta para a esquerda, justamente para tentar conter o movimento original da
barra para a direita; o valor dessa força magnética induzida é:

Fmag .induzida  iinduzidaBsen


( Bv)
Fmag .induzida 
Bsen90 o
R


B 2 2v
Fmag .induzida 
R

onde γ é o ângulo entre a corrente induzida e o campo magnético externo B ; no caso γ = 90o.
Aqui desconsideramos o sinal negativo de iinduzida já que estamos calculando apenas o módulo
da força magnética induzida.
Todo este conjunto de grandezas induzidas é mostrado na figura abaixo.

B

n̂
io
ε
+
io
iind
.
x

Fmag .ind.

Bind .
ℓ

v

Fmagnética
Voltando a aplicar a Lei das Malhas sobre este circuito, considerando agora a presença da fem
induzida, teremos:
 Vi  0     induzida  Ri  0
  Bv  Ri  0


  Bv  Ri ,
i
onde i  io  iinduzida , é a corrente resultante no circuito. A subtração entre as duas correntes
deve-se ao fato de elas terem sentidos opostos.
b) Sobre a barra atuam duas forças: a força magnética original e a induzida, portanto, a Lei
Fundamental da Dinâmica (Segunda Lei de Newton) sobre a barra resulta em:
 Fi  ma

i
 Fi  m
i

dv B B 2  2 v
m 

dt
R
R

dv B B 2  2 v


dt mR
mR
dv
dt

m
dv
 Fmagnética  Fmag . induzida
dt
dv B B 2  2 v
m 

dt
R
R

dv B
  Bv 

dt mR

c) A velocidade e a corrente limites são alcançados quando as forças sobre a barra se igualam,
ou seja, quando
Fmagnética  Fmag . induzida

  Bv  0


dv
0
dt
v

B
  Bv   0
mR

B
Quando a barra atinge essa velocidade, a corrente resultante terá o valor:
  Bv  Ri

  
  Ri
 B 
  B
Ou seja, na velocidade limite: i  0

Ri    

io  iinduzida  0


Ri  0

i 0A
io  iinduzida .
Quer dizer que a corrente induzida assume o mesmo valor da corrente original, mas elas têm
sentidos contrários e se anulam.
Reparem que a velocidade da barra estava aumentando até atingir essa velocidade limite, em
conseqüência, a taxa de variação temporal (a derivada com o tempo) do fluxo magnético também
estava aumentando já que ela dependia da velocidade, em razão disso a fem induzida também
aumentava com o objetivo de conter aquela tendência do fluxo. Contudo, quando a barra atinge a
velocidade limite, a taxa de variação do fluxo com o tempo passa a ser constante, daí a fem
induzida também se torna constante. Embora o fluxo em si continue a aumentar porque a
coordenada x, da qual ele depende, ainda permaneça aumentando, a sua taxa de variação
passou a ser constante e a fem induzida depende é dessa taxa.
##############################################################################
2) a) Sobre a barra colocada no plano inclinado atua a componente paralela à rampa da força da


gravidade: P//  P sen  mgsen  , com sentido descendente (negativo, portanto).
A barra delimita uma área sobre o plano inclinado e, portanto, determina também um fluxo
magnético que atravessa essa área dado por:
 B  BAcos
 B  Bx' cos ,


Note que o ângulo α entre o campo magnético e o versor n̂ normal à superfície atravessada pelo
campo é, neste caso, igual ao próprio ângulo θ do plano inclinado como a figura abaixo procura
demonstrar.
N
ℓ

Psen
x’

B

v
θ

n̂
M
R
θ
Conforme a barra desliza pelo plano inclinado, ocorre uma variação do fluxo magnético e
então são induzidas uma força eletromotriz e uma corrente, ambas no sentido anti-horário. Essa
corrente induzida interage com o campo magnético, gerando uma força magnética induzida sobre
a barra que busca opor-se à tendência de descida desta. Portanto, pela Lei de Faraday-Lenz:
 induzida  

E:
d B
dt
 induzida  

d [ Bx' cos ]
dt

 induzida   B cos
 induzida   Bv cos
iinduzida 
 induzida
R

iinduzida 
 Bv cos
.
R
dx'
dt
E ainda:

Fmag .induzida  iinduzidaBsen

( Bv cos )
Fmag .induzida 
Bsen 90 o
R


B 2  2 v cos
Fmag .induzida 
R

onde γ é o ângulo entre a corrente induzida e o campo magnético que vale, neste caso, 90 o.
No entanto, esta força magnética não é paralela ao plano inclinado, portanto é preciso
determinar a sua projeção na direção do plano inclinado que será dada pelo produto entre seu
módulo e o cosseno do ângulo θ, ou seja:
Fmag.induzida //  Fmag.induzida cos  B  vRcos 


2 2
2
A figura abaixo procura ilustrar todas essas idéias:
Fmag.induzida //


B

Fmag .induzida
x’
θ

v 
Psen
iinduzida
R
θ
Aplicando a Segunda Lei de Newton à barra teremos:
 Fi  ma
i


 Fi  m
i
dv
dt
dv B 2  2 v.cos2
m 
 mgsen
dt
R

m
dv
 ( Fmag . induzida ) //  mgsen
dt
A velocidade limite (terminal) da barra é alcançada quando as forças se igualam, ou seja,
quando a aceleração se anula e a barra passa a se mover com velocidade constante, portanto:
a0


dv
0
dt


B 2  2 v.cos2
 mgsen
R
v
mgRsen


B  cos cos
2 2
Na última passagem usei a relação: tan  
B 2  2 v.cos2
 mgsen  0
R
v
v
mgRsen
B 2  2 cos2
mgR tan 
B 2  2 cos
sen
.
cos
b) Aqui devemos demonstrar que a energia potencial gravitacional da barra é inteiramente
convertida em energia elétrica, ou melhor, é convertida em energia térmica através da sua
dissipação no resistor do circuito.
Nesse resistor temos uma potência dissipada dada por: Pdissipada  Ri , onde a corrente i é
2
a induzida pelo movimento da barra. Assim:
Pdissipada 
2
Riinduzida

 Bv cos 
Pdissipada  R

R


2

Pdissipada 
B 2  2 v 2 cos2 
R
Introduzindo nesta expressão o valor da velocidade limite determinada no item anterior,
encontramos:
B 2  2 cos2   mgR tan  
Pdissipada 
 2 2

R
 B  cos 
2

Pdissipada 
m 2 g 2 R tan 2 
B 2 2
A energia potencial gravitacional da barra deve ser a origem dessa energia sendo dissipada.
Tal energia é obtida de:
U gravitacional  mgh

U gravitacional  mgx' sen
,
onde h é a altura que a barra está do solo e que pode ser obtida neste caso da relação:
sen 
h
x'

h  x' sen
Para obter a potência fornecida devemos derivar esta energia potencial pelo tempo, dessa
forma:
Pfornecida 
dU gravitacional
dt

Pfornecida 
d [mgx' sen ]
dt

Pfornecida  mgsen
d [ x' ]
dt
Pfornecida  mgvsen

Substituindo aqui a velocidade pelo valor determinado no item passado, encontramos:
Pfornecida
 mgR tan  
 mg 2 2
sen
 B  cos 

Pfornecida 
m 2 g 2 R tan 2 
B 2 2
,
Fica demonstrado então que: Pdissipada = Pfornecida, ou seja, fica evidenciada a Conservação da
Energia no processo.
##############################################################################
10)
d
h

v

B
ℓ
a) A espira adentra a região com campo magnético uniforme no instante que convencionaremos
como sendo t = 0 s, e nesse momento ela está numa posição que especificaremos como
xo = 0 m.

B
t=0s
x = xo = 0 m
O detalhe significativo deste exercício é que o fluxo magnético tem que ser calculado em três
situações distintas:
I) quando a espira está invadindo a região na qual o campo magnético está confinado;
II) quando a espira está inteiramente dentro daquela região;
III) quando a espira está deixando a referida região.
Em cada uma dessas etapas teremos um fluxo distinto e, em conseqüência, uma fem induzida
específica. Calculemos o fluxo em cada uma dessas situações:
I) Enquanto a espira invade a região magnetizada, a área dela que é atravessada pelo campo é

dada por: A = hx, onde h = 5 cm = 0,05 cm. Consideremos um versor n̂ normal à espira tendo
sentido para baixo, de maneira a formar um ângulo de 0 o com o campo magnético.
0s < t < 5s

 n̂
h
x
Com esse detalhe, o fluxo magnético através da espira, enquanto ela invade a região coberta
pelo campo, é:
 B ( I )  BAcos

 B ( I )  Bhxcos0o

 B ( I )  Bhx
Mas, esta espira desloca-se na direção x com velocidade constante, portanto ela desenvolve um
x  xo  vt , onde, como já
movimento retilíneo uniforme (MRU), cuja equação horária é:
estabelecemos, xo = 0 m. Assim:
x  vt , simplesmente. Portanto:
 B ( I )  Bhx

 B ( I )  Bhvt
Ingressando com os valores numéricos temos:
 B ( I )  Bhvt

 B ( I )  (1,0 T )(0,05 m)(0,02 m/s )t
 B ( I )  (1,0  10  3Wb / s)t


 B ( I )  (1,0 mWb/s)t
Temos assim o fluxo magnético em função do tempo, mas este resultado só é válido até a
espira invadir totalmente a região com campo magnético, o que ocorre no instante em que ela
percorre uma distância d = 10 cm = 0,10 m, ou seja em:
x  vt

d  vt

t
d
v

t
0,10 m
0,02 m/s

t  5s.
A partir desse instante o valor do fluxo vai mudar.
t=5s

 n̂
h
d
II) Quando a espira estiver completamente dentro da região com campo magnético o fluxo
através dela será constante, uma vez que tanto a área quanto a intensidade do campo não
variam mais. Embora a espira ainda se mova, sua área permanece a mesma e ela vai
atravessando regiões em que o campo magnético tem sempre o mesmo valor (assim como
mesma direção e sentido), isto acarreta uma uniformidade do fluxo magnético também. De fato,
agora:
 B ( II )  BAcos

 B ( II )  Bhd cos0o

 B ( II )  Bhd,
onde d = 10 cm = 0,10 m. Nenhum dos fatores que compõe o fluxo aqui se alteram com o
tempo; o fluxo é, portanto, constante.
Numericamente:
 B ( II )  Bhd


 B ( II )  (1,0 T )(0,05 m)(0,10 m)

 B ( II )  5  10 3 Wb
 B ( II )  5 mWb
Como a espira demorou 5 s para entrar completamente na região com campo, levará mais 5 s
para sua aresta dianteira atingir a extremidade oposta da região, ou seja, ao todo demorará 10 s
para começar a sair da área com campo. De fato, tendo essa área um comprimento
ℓ = 20 cm = 0,20 m, então, o tempo necessário para a espira atravessar a região é:
x  vt

  vt

t

v

t
0,20 m
0,02 m/s

t  10 s
A partir desse momento, a área da espira em contato com o campo passará a diminuir.
t = 10 s

 n̂
d
ℓ
h
III) Como o desenho abaixo procura mostrar, a área da espira em contato com o campo
magnético passa a ser:
A    (x  d )

A  (  d )  x
10 s < t < 15 s

 n̂
h
d
x
ℓ
Assim, o fluxo magnético na área da espira que ainda permanece dentro da região com campo
magnético é:
 B ( III )  BAcos


 B ( III )  Bh [(  d )  x] cos0 o
 B ( III )  Bh [(  d )  x]

 B ( III )  Bh [(  d )  vt ]
Entrando com os valores numéricos temos:
 B ( III )  Bh [(  d )  vt ]   B ( III )  (1,0 T )(0,05 m)[(0,20 m  0,10 m)  (0,02 m/s )t ]

 B ( III )  (1,5  10  2 Wb)  (1  10  3 Wb / s)t

 B ( III )  (15 mWb)  (1 mWb / s)t
Quando x = (ℓ + d) = (20 cm + 10 cm) = 30 cm = 0,30 m, a espira sairá completamente
da região sob influência do campo magnético. A partir desse momento não haverá mais fluxo
magnético a ser calculado:
x  vt

  d  vt

t
d
v

t
0,30 m
0,02 m/s

t  15 s
t = 15 s

 n̂
d
x
ℓ
Um gráfico representando o comportamento do fluxo magnético durante o movimento da espira
teria o seguinte aspecto:
 B (mWb)
5
t(s)
0
5
10
15
b) A fem induzida também terá um valor específico em cada uma dessas etapas do movimento
da espira. Aplicando a lei de Faraday-Lenz a cada uma delas encontraremos:
I) Para 0 s < t < 5 s:
 (I )  

d B ( I )
dt

 (I )  
d [(1,0 mWb/s)t ]
dt

 ( I )  (1,0 mWb/s)
 ( I )  1,0 mV
II) Para 5 s < t < 10 s:
 ( II )  
d B ( II )
dt

 ( II )  
d [(5,0 mWb)]
dt

 ( II )  0 V
d [t ]
dt
III) Para t > 10 s:
 ( III )  
d B ( I )
 ( III )  

dt
d [(15 mWb)  (1 mWb / s)t ]
dt
d [t ] 
 d [15 mWb]
 (1,0 mWb/s)

dt
dt 

 ( III )  


 ( III )  1,0 mV
O gráfico da fem induzida em função do tempo seria então:
 (mV )
1
0
5
10
t (s)
15
–1
##############################################################################
11) a) A barra juntamente com as guias delimita uma área que é atravessada pelo campo
magnético redundando no aparecimento de um fluxo magnético dado por:
 B  BAcos

 B  Bx cos0o

 B  Bx .

Como vê-se na figura abaixo escolhemos um versor n̂ normal à essa área e com sentido para
dentro, de tal forma a fazê-lo paralelo ao campo magnético e, assim, ter θ = 0o.
A fem induzida será dada pela lei de Faraday-Lenz:
 induzida  

d B
dt

 induzida  
d [ Bx]
dt

 induzida   B
d [ x]
dt
 induzida   Bv
Introduzindo os valores numéricos encontramos, em módulo:
 induzida  (2,5 T )(0,20 m)(4 m/s )

 induzida  2 V

B
iinduzida

 n̂

v
ℓ

Fmag .ind.
R
x
b) O sentido em que a corrente se estabelece está indicado na figura acima. A força magnética
induzida que essa corrente produz deve se opor ao movimento da barra para tentar conter o
aumento do fluxo que se dá devido ao aumento da área. Para que surja uma força magnética
com o sentido contrário ao da velocidade a corrente elétrica induzida deve ter o sentido horário.
Com isso e usando-se a regra da mão direita constata-se que a força magnética tem o sentido
correto.




Usando a Lei das Malhas de Kirchhoff   Vi  0  teremos a seguinte equação para
i
descrever esse circuito:
 Vi  0
i
O que resulta em:

  Riinduzida  0
iinduzida 
2V
0,8 
  Riinduida



iinduzida 

R
iinduzida  2,5 A
Portanto, a corrente induzida vale 2,5 A e tem sentido anti-horário.
##############################################################################
12) Neste exercício o enunciado já é claro quanto ao fato de o campo magnético ser
perpendicular à área que ele atravessa, portanto, cosθ = 1. Daí:
 B  BAcos

 B  BA
 dB

 2 T / s  (o sinal negativo é porque o
 dt

A área é fixa, mas o campo magnético está variando 
campo está diminuindo), portanto:
 induzida  
d B
 induzida  

dt
d [ BA]
dt
 induzida  (1 m 2 )( 2 T / s)

 induzida   A

dB
dt
 induzida  2 V

Agora, aplicando a lei de Ohm para essa espira obteremos:
iinduzida 
 induzida

R
iinduzida 
2V
4

iinduzida  0,5 A
##############################################################################
13) Novamente o enunciado do exercício já anuncia que o campo é perpendicular à área
atravessada por ele, portanto, θ = 0o e cosθ = 1. O fluxo magnético será dado por:
 B  BAcos

 B  BNAespira
Onde levamos em conta que se trata de uma bobina com N espiras de área A cada uma.
A fem induzida nessa bobina é obtida pela aplicação da lei de Faraday-Lenz:
 induzida  
d B
dt

 induzida  
d [ BNAespira ]
dt

 induzida   NAespira
dB
dt
A área não está mudando neste caso, mas apenas o campo e temos como determinar qual é a
sua taxa de variação:
dB B B final  Binicial


dt t
t

dB 0 T  0,01 T

dt
1s

dB
 0,01 T / s
dt
Portanto:
 induzida   NAespira

dB
dt

 induzida  (200)[ (0,04 m) 2 ](0,01 T / s)
 induzida  0,01V
##############################################################################
14) O gráfico apresentado do fluxo magnético em função do tempo é muito similar ao obtido no
exercício 10 acima, apenas diferindo nos valores. Conforme veremos, o gráfico da fem induzida
também será semelhante ao daquele exercício.
No intervalo de tempo 0 s ≤ t ≤ 0,1 s, o fluxo aumenta linearmente com o tempo. Ou
seja:  B  a  bt , é a equação de uma reta cujos coeficientes, a e b, devemos determinar. O
coeficiente angular dessa reta pode ser obtido de:
b
 B , final   B , inicial
t final  tinicial

b
4 Wb  0 Wb
0,1 s

b  40 Wb / s .
Já o coeficiente linear a é claramente igual a 0 Wb neste segmento. Dessa forma obtemos:
 B  (40 Wb / s)t para 0 s ≤ t ≤ 0,1 s.
Determinemos o valor da fem induzida neste intervalo:
 induzida  
d B
dt

 induzida  
d[(40 Wb / s)t ]
dt
 induzida  40 V

Agora, no intervalo 0,1 s ≤ t ≤ 0,3 s, vemos que o fluxo magnético é constante:
 B  4 Wb .
Obviamente então:
 induzida  
d B
dt

 induzida  
d[4Wb]
dt

 induzida  0 V
Finalmente, no intervalo 0,3 s ≤ t ≤ 0,4 s, vê-se que o fluxo decresce linearmente com o
tempo, ou seja, novamente:  B  a  bt , onde agora:
b
 B
t

 B , final   B , inicial
t final  tinicial

b
0 Wb  4 Wb
0,4 s  0,3 s

b  40 Wb / s .
Para encontrar a usaremos o fato que quando t = 0,4 s temos  B  0 Wb , e daí:
 B  a  bt


a  (40 Wb / s)(0,4 s)  0
a  16 Wb
O fluxo magnético nesse intervalo é, portanto:
 B  16 Wb  (40 Wb / s)t ,

a  16 Wb  0
resultando em:
 induzida  
d B
 induzida  

dt
d[16 Wb  (40 Wb / s)t ]
dt
 induzida  40 V

Combinando em um gráfico todos esses resultados da força eletromotriz em cada intervalo
obtemos:
 (V )
40
0
0,1
0,2
0,3
t(s)
0,4
–40
##############################################################################
15) Sobre a barra atuam três forças:
I) O seu próprio peso Pbarra = mg;
II) A tensão exercida pelo peso do bloco pendurado que indicarei simplesmente por Pbloco = Mg.
Estas duas forças apontam para baixo.
III) Uma força magnética com sentido para cima e que equilibra o sistema. Esta força nasce da
interação entre o campo magnético externo e a corrente elétrica produzida pela bateria; seu
sentido é obtido a partir da aplicação da regra da mão direita, e sua intensidade é:

Fmagnética  io Bsen


Fmagnética  io Bsen90 o


Fmagnética  io B,
onde β é o ângulo entre o campo magnético e a corrente; neste caso β = 90o.




Aplicando a Lei das Malhas de Kirchhoff   Vi  0  temos a seguinte equação para descrever
i
esse circuito:
 Vi  0
i

  Rio  rio  0

  ( R  r )io  0

onde ε é a fem fornecida pelo gerador presente, e r é a resistência da barra.
Dessa forma, a força magnética toma a forma:

Fmagnética 

rR
B
io 

Rr
,
A figura abaixo ilustra essa composição de forças.
y
ε
R = 20 Ω

B
yo

Fmagnética

g
io
0

Pbarra
M

Pbloco
a) Aplicando a 2ª. Lei de Newton a esse sistema de forças, encontramos:
 Fi  ma

i
 Fi  m
i
dv
dt

m
dv
 Fmagnética  Pbloco  Pbarra
dt
Como todas as forças estão na direção y, não foi necessário adotar a notação vetorial, bastando
apenas indicar os sentidos das forças com os sinais adequados (seguindo a convenção mostrada
no desenho).
Como o sistema está equilibrado, então a aceleração é nula, e, portanto, a soma das forças
também é zero (a resultante de forças é nula). Assim, temos:
Fmagnética  Pbloco  Pbarra  0


rR
B  ( M  m) g  0

io B  Mg  mg  0


(r  R)( M  m) g
B
Introduzindo os valores numéricos fornecidos, obtemos:
(5   20 )(18 kg  2 kg )(10 m / s 2 )

(1,0 m)(1,0 T )

  5000V
b) Quando o bloco é desconectado da barra, o equilíbrio de forças é quebrado e a barra passa a
subir. Dessa forma, a área delimitada por ela e pelo circuito passa a se alterar, produzindo uma
variação do fluxo magnético e, conseqüentemente, gerando uma força eletromotriz, uma corrente
e uma força magnética induzidas no sistema que tentam impedir o movimento da barra.
desenho abaixo procura ilustrar a nova composição de forças que surge.
O
y
io

B

Fmagnética

v

n̂ 
yo
iinduzida

Pbarra
y
0

Fmag .induzida
Equacionando este sistema de força encontramos agora que:
 Fi  m
i
dv
dt

m
dv
 Fmagnética  Pbarra  Fmag .induzida
dt
Para determinarmos o valor dessa força magnética induzida devemos calcular o fluxo

magnético e dele obter a força eletromotriz induzida. Considerando um versor n̂ normal à área
apontando para dentro da página (vide figura acima), resulta que o ângulo entre o campo e o
versor é zero, portanto:
 B  BAcos

 B  B( yo  y) cos0o 
 B  B( yo  y)
Aplicando a lei de Faraday-Lenz:
 induzida  

d B
dt

 induzida  B
dy
dt
 induzida  
d [ B( yo  y )]
dt

 induzida  Bv

 induzida   B
d ( yo  y )
dt
onde v é a velocidade de deslocamento da barra. Lembrando que yo é uma constante e sua
derivada é nula.
Daí podemos obter a corrente elétrica induzida:
iinduzida 
 induzida
rR

iinduzida 
Bv
rR
Da interação entre esta corrente e o campo magnético origina-se a força magnética induzida:
Fmág .induzida  iinduzidaBsen

Fmág .induzida 

Fmág .induzida 
Bv
Bsen 90 o
rR
B 2 2v
rR
Introduzindo este resultado na equação de movimento da barra temos:
dv
m  Fmagnética  Pbarra  Fmag .induzida
dt

m
dv
B
  Bv   mg

dt r  R


dv

B 2 2v
m 
B  mg 
dt r  R
rR
dv
B
  Bv   g

dt m(r  R)
Na última passagem simplesmente dividi os dois lados da expressão por m.
Colocando nessa expressão os valores numéricos já conhecidos, encontramos:
dv
(1,0 T )(1,0m)

[5000 V  (1,0 T )(1,0 m)v]  (10 m / s 2 )
dt (2 kg )(5   20 )

dv
 90  0,02v
dt
Neste resultado abolimos as unidades por questão de facilidade de manuseio das expressões,
mas você pode realizar uma análise dimensional e conferir se tudo está coerente.
Temos agora uma pequena equação diferencial para resolver. Devemos multiplicar ambos os
lados pela diferencial dt para poder separar as variáveis e integrar, dessa forma obteremos o
comportamento da velocidade da barra com o tempo. Então:
dv
dt  90  0,02vdt
dt

dv
 dt
90  0,02v 

v
t
dv'


 dt'


90

0
,
02
v
'
0
0
Explicando os limites de integração adotados: na primeira integral, o limite inferior é a
velocidade inicial da barra que era zero, uma vez que ela estava parada quando o bloco M foi
retirado; o limite final é a velocidade num instante t qualquer (fizemos uma distinção na variável
de integração para não confundi-la com essa variável do extremo da integral). Na segunda
integral, o limite inferior é zero porque começamos a contar o tempo no instante em que o bloco
M foi liberado; o limite superior é um instante t qualquer.
Resolvendo as integrais encontramos:
v
t
dv'


 dt'


90

0
,
02
v
'
0
0
v
ln( 90  0,02v' )
 t'
(0,02)
0


ln( 90  0,02v)  ln( 90)  0,02t

ln( 90  0,02v)  4,5  0,02t

t
0
ln( 90  0,02v)  4,5  0,02t
Aplicando a exponencial aos dois lados dessa expressão teremos:
ln( 90  0,02v)  4,5  0,02t

90  0,02v  e 4,5 e  0,02 t

 0,02v  90  90e  0,02 t

v  4500 1  e  0,02 t m/s

90  0,02v  e 4,5  0,02 t

90  0,02v  90e  0,02 t




 0,02v  90 1  e  0,02 t


Portanto, a velocidade da barra tende exponencialmente a um valor limite. (Tente desenhar o
gráfico desta função num programa como o Excel, por exemplo, e visualize o comportamento da
velocidade com o tempo.)
c) A velocidade limite é alcançada quando
dv
0
dt

90  0,02v  0
dv
 0, portanto:
dt

0,02v  90

v  4500 m/s.
##############################################################################
16) No instante inicial (t = 0), a barra AB é abandonada sobre os fios fechando o circuito. Nesse
instante há duas forças agindo sobre ela:
I) O seu próprio peso Pbarra = mg; e
II) A força magnética produzida pela interação entre o campo magnético e a corrente elétrica
que circula no circuito formado pela barra e os fios. Essa força é dada, como sempre, por:

Fmagnética  io Bsen



Fmagnética  B,
R
onde β é o ângulo entre o campo magnético e a corrente; neste caso β = 90o, e ε é a fem
fornecida pelo gerador presente.
A figura abaixo ilustra essas forças e indica que a força magnética aponta para baixo, segundo
a regra da mão direita.
Em t = 0 s
ε
R

B

n̂ 
io

Pbarra

Fmagnética
A partir do momento em que a barra começa a mover-se para baixo, a área por ela delimitada
passa a variar e, em conseqüência, ocorre também uma variação do fluxo magnético dando
origem a uma força eletromotriz e a uma corrente elétrica induzidas. A interação desta corrente
com o campo magnético produz uma força magnética induzida que tende a se contrapor ao
movimento da barra (vide figura abaixo). Como na questão anterior podemos determinar o valor
dessa força magnética seguindo o roteiro padronizado.
io

B

n̂ 
iinduzida

Fmag .induzida
y

Pbarra

v

Fmagnética

Associando-se um versor n̂ normal à área e com sentido para dentro, resulta que o ângulo
entre o campo e esse versor é zero, portanto:
 B  BAcos

 B  By cos0o 
 B  By
Aplicando a lei de Faraday-Lenz:
 induzida  
d B
dt

 induzida  
d [ By ]
dt

 induzida   B
dy
dt
 induzida   Bv,

onde v é a velocidade de deslocamento da barra.
Daí podemos obter a corrente elétrica induzida:
iinduzida 
 induzida
R

iinduzida 
 Bv
,
R
Da interação entre esta corrente e o campo magnético origina-se a força magnética induzida:
Fmag .induzida  iinduzidaBsen

Fmag .induzida 
Bv
Bsen 90 o
R
B 2 2v
Fmag .induzida 
R

Equacionando o sistema de força encontramos que (adotando o sentido positivo do eixo y como
sendo para baixo, conforme se vê na figura acima), temos:
 Fi  m
i
dv
dt

m
dv
 Fmagnética  Pbarra  Fmag .induzida
dt
dv 
B 2 2v
 m  B  mg 
dt R
R

dv B
  Bv   g

dt mR

m
dv B
  Bv   mg

dt R
Ingressando com os valores numéricos conhecidos, obtemos:
dv B
  Bv   g

dt mR


dv (0,5T )( 2m)

[10V  (0,5T )( 2m)v]  (10 m / s 2 )
dt (2kg )(10)
dv
 10,5  0,05v
dt
Novamente, trata-se de uma pequena equação diferencial a ser resolvida pelo método de
separação de variáveis já usado no exercício anterior:
dv
dt  (10,5  0,05v)dt
dt
dv
 dt
(10,5  0,05v)


v
t
dv'
  dt'
0 (10,5  0,05v ' ) 0

v

ln(10,5  0,05v)
t
 t' 0
 0,05
0

ln(10,5  0,05v)  0,05t  2,35


10,5  0,05v  e 2,35 e  0,05 t
 0,05v  10,5  10,5e  0,05 t

 0,05v  10,5(1  e  0,05 t )

ln(10,5  0,05v)  ln(10,5)  0,05t

10,5  0,05v  e  0,05 t  2,35
v  210 (1  e  0,05 t ) m/s

Já a corrente em função do tempo será obtida de:
i  io  iinduzida


B 2 2v
,
i 
R
R
onde i aqui é a corrente resultante.
Colocando nesta expressão os valores numéricos conhecidos, e também a velocidade recém
obtida, teremos:

B 2 2v
i 
R
R


(10 V ) (0,5 T ) 2 (2 m) 2 (210 m/s )
i

(1  e  0,05 t )
(10 )
10 
i  [1  21(1  e  0,05 t )] A

i  (20  21e  0,05 t ) A
b) Como sempre, a velocidade limite é alcançada quando a aceleração se anula, portanto:
dv
0
dt

 (10,5  0,05v)  0

v  210 m/s
Este resultado também pode ser obtido através da expressão para a velocidade em função do
0,05 t
tempo, v  210 (1  e
( t   ). Neste caso:
) m/s , buscando-se seu valor quando o tempo tende ao infinito


lim e  0,05t  0,
t 
portanto:
v(t  )  lim [210(1  e 0,05t ) m/s]
t 

v  210 m/s .
Reparem, contudo, que a corrente resultante não é nula quando se atinge esta velocidade
limite. De fato:
i(t  )  lim [(20  21e 0,05t ) A]
t 

i  20 A
Esta corrente residual se faz necessária para gerar uma força magnética que compense o
peso da barra e mantenha esta movendo-se com velocidade constante. O sinal negativo nela
indica que esta corrente tem sentido oposto à corrente original produzida pelo gerador.
##############################################################################
17) a) Se o bloco M sobe com velocidade constante é porque a barra move-se para a direita e a
resultante de forças sobre ela é nula. Nessa barra atuam três forças que nos interessam neste
caso:
I) A tensão T exercida pelo peso do bloco M, portanto T = Mg;
II) Como há uma corrente passando pela barra então deve haver uma força magnética produzida
pela interação dessa corrente com o campo magnético presente. Essa força deve ter o sentido
para a direita na figura uma vez que se faz necessária uma força com essa característica para
compensar a tensão T, e assim manter a velocidade da barra constante. Para que, num campo
magnético com a direção indicada, apareça uma força magnética horizontal apontando para a
direita, é necessário que a corrente circule no sistema no sentido anti-horário (regra da mão
direita). Com essa exigência já se pode então definir a polaridade do gerador G e ela é mostrada
na figura abaixo.
A intensidade dessa força magnética é dada por:

Fmagnética  io Bsen


Fmagnética 

Fmagnética 


rR

rR
Bsen90 o
B,
onde β é o ângulo entre o campo magnético e a corrente, neste caso β = 90o, e ε é a fem
fornecida pelo gerador presente.
Mas notem, contudo, que esta força magnética não aponta para a direita, mas faz sim um
ângulo de 30º em relação ao plano da barra, portanto, para determinarmos o valor exato da força
que arrasta a barra devemos determinar a projeção dessa força magnética no plano da espira.
Isto resulta em:
 F
magnética
//  F
magnética
cos30 o 
0,87
B
rR
Na figura abaixo procuro demonstrar todos esses detalhes.

B

B

Fmagnética
30o
R

n̂
60o

Pbloco
30o 

v
Fmagnética //
–
G
+
io
x
III) Devido ao movimento da barra, a área delimitada por ela e pelos trilhos passa a se alterar,
produzindo uma variação do fluxo magnético e, conseqüentemente, gerando uma força
eletromotriz,uma corrente e uma força magnética induzidas que tentam se opor ao deslocamento
da barra.

Escolhendo o versor normal ( n̂ ) à área delimitada pelos trilhos e pela barra com sentido para
cima, observa-se na figura que isto resulta num ângulo de 30o entre ele e o campo magnético,
assim, a intensidade da força magnética induzida é obtida através dos seguintes passos:
i) Fluxo Magnético:
 B  BAcos

 B  Bx cos30 o

 B  0,87 Bx
ii) FEM Induzida:
 induzida  

d B
dt

 induzida  
d [0,87 Bx]
dt

 induzida  0,87 B
dx
dt
 induzida  0,87 Bv,
iii) Corrente Induzida:
iinduzida 
 induzida

rR
iinduzida 
 0,87 Bv
rR
iv) Força Magnética Induzida:
Fmág .ind .  iinduzidaBsen

Fmág .ind .

Fmág .ind . 
0,87 Bv
Bsen 90 o
rR
0,87 B 2  2 v

rR
Mas também esta força magnética não está contida no plano da espira, conforme a figura
abaixo procura mostrar. Para obter a sua projeção sobre o plano da espira devemos fazer:


0,87 B 2  2 v
Fmág .ind. //  Fmág .ind. cos30 o 
cos30 o
rR


0,75 B 2  2 v
Fmág .ind. // 
rR

B
io

B
R

Fmag .ind. //

Fmag .ind.

n̂

Pbloco
bloco

v

Fmagnética //
G
iinduzida
x
Entrando com este conjunto de forças na 2ª. Lei de Newton, temos:
 Fi  m
i
dv
dt

m
dv
 Fmagnética //  Fmag .ind . //  Pbloco
dt

dv 0,87
0,75 B 2  2 v
m 
B 
 Mg
dt r  R
rR

m

dv
B
0,87  0,75 Bv   M g

dt m(r  R)
m
dv
B
0,87  0,75 Bv   Mg

dt r  R
Substituindo os termos pelos valores conhecidos chega-se a:
dv
(0,5 T )(1,2 m)
(10 kg )

[0,87  (0,75)(0,5 T )(1,2 m)(5 m/s )] 
(10 m/s 2 )
dt (1 kg )(5   10 )
(1 kg )

dv
 0,0348  0,09  100
dt

dv
 0,0348  100,09
dt
Devemos lembrar agora que a barra está-se movendo com velocidade constante, portanto:
dv
0
dt

0,0348  100,09  0

  2876,17 V
b) No instante inicial (t = 0), desconecta-se o bloco da barra e assim se elimina a tração que
este exercia sobre a ela, a equação do movimento assume então a seguinte configuração:
 Fi  m
i
dv
dt

m
dv
 Fmagnética //  Fmag .ind . //
dt

dv 0,87
0,75 B 2  2 v
m 
B 
dt r  R
rR

dv
B
0,87  0,75 Bv 

dt m(r  R)

m
dv
B
0,87  0,75 Bv 

dt r  R
Fazendo a atribuição dos valores numéricos temos:
dv
(0,5 T )(1,2 m)

[(0,87 )( 2876 ,17 V )  (0,75)(0,5 T )(1,2 m)v]
dt (1 kg )(5   10 )

dv
 100,09  0,018v
dt
Novamente surge uma pequena equação diferencial para resolver:
dv
dt  (100,09  0,018v)dt
dt

v
dv
 dt
(100,09  0,018v)
v
ln(100,09  0,018v)
t
 t' 0
 0,018
5 m/s

t
dv'


 dt'
5 m/s (100 ,09  0,018 v ' ) 0

ln(100,09  0,018v)  ln[100,09  0,018(5)]  0,018t

ln(100,09  0,018v)  ln(100,09  0,09)  0,018t

ln(100,09  0,018v)  4,605  0,018t

ln(100,09  0,018v)  ln(100 )  0,018t

ln(100,09  0,018v)  4,605  0,018t

Aplicando a exponencial aos dois membros desta expressão, obtém-se:
100,09  0,018v  e 4,605 e 0,018 t


v  5560 ,56  5555,56e  0,018 t m/s
 0,018v  100,09  100 e 0,018 t

v  [5555,56(1  e  0,018 t )  5] m/s
A diferença entre este resultado e o apresentado na apostila deve-se ao fato de nesta o autor
não ter considerado que a velocidade inicial da barra era de 5 m/s (no momento em que se solta
o bloco preso a ela). Reparem que considerei o limite inferior da integração iniciada acima como
sendo essa velocidade, provavelmente o autor esqueceu-se deste detalhe e iniciou sua
integração com velocidade nula. Isto configura um problema, pois se usarmos o resultado da
apostila no instante t = 0 s, veremos que resulta numa velocidade nula nesse momento, o que
não está correto. Já o resultado aqui obtido fornece a velocidade inicial exata.