Medidores de Grandezas elétricas
Aula 05
Prof. Valner.
Bibliografia: Instrumentação e Fundamentos de
Medidas Balbinot, A., Brusamarello, V., vol. 1
Instrumentos Analógicos e Digitais
Analógicos: Eletromecânicos – utilizam geralmente um ponteiro
deslocando-se sobre uma escala para indicar a medida
Digitais: Eletrônicos – Geralmente utilizam dígitos para indicar a
medida.
Classes dos Instrumentos
Índice de Classe
Limites de erros
0 05
0,05
0 05%
0,05%
0,1
0,1%
0,2
0,2%
05
0,5
0 5%
0,5%
1,0
1,0%
1,5
1,5%
25
2,5
2 5%
2,5%
5,0
5,0%
Os erros são sempre relativos ao
fundo de escala sendo utilizado na
medida.
Multímetro Digital de Bancada
- 740 01
Classe 0,05% + 2 dgt.
4,5 dígitos 50000 Count
True RMS Multimeter
Permanent moving moving-coil instrument
class 1.5
1 5 / double scale
Instrumentos Analógicos
IInstrumento
t
t Básico:
Bá i
Galvanômetro:
G l
ô t Bobina
B bi
que pela passagem de corrente provoca um
movimento numa parte móvel
móvel.
Voltímetro: acrescentando-se resistores em
série
Amperímetro: acrescentando-se em paralelo
Ohmímetro
Oh í t : acrescentando-se
t d
uma pilha
ilh
Esses componentes e suas ligações são
selecionados
l i
d por uma chave
h
adequada,
d
d d
de
modo a permitir a leitura da grandeza de
interesse.
interesse
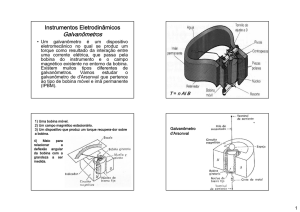
Galvanômetro de Ferro Móvel
- Galvanômetro tipo ferro móvel; resistores são conectados
em série p
para transformá-lo num voltímetro, p
por exemplo
p .
Galvanômetro de Ferro Móvel
Galvanômetro de Ferro Móvel
Muito utilizados como instrumentos de painel
p
Duas barras de ferro adjacentes são magnetizadas
(através da corrente em uma bobina na qual as barras
estão
tã inseridas)
i
id ) de
d maneira
i uniforme,
if
surge uma
força de repulsão entre ambas uma vez que as duas
adquirem a mesma polarização magnética
Faz-se uma barra fixa e a outra móvel, adaptando-se
um ponteiro na barra móvel
Esse tipo de instrumento pode ler voltagens ou
correntes contínuas e alternadas
D fl ã d
Deflexão
do ponteiro
t i é proporcional
i
l ao quadrado
d d d
da
corrente; assim, esse tipo de instrumento mede valor
RMS,, também chamado de valor eficaz
Galvanômetro do tipo Bobina
Móvel
Galvanômetro de bobina móvel (D’Arsonval)
(
)
Galvanômetro de D'ARSONVAL
Instrumento de bobina móvel – usado na maioria
dos multímetros analógicos
g
.
Galvanômetro do tipo Bobina
Móvel
Quando uma corrente elétrica é aplicada
p
na
bobina (condutor) tem-se a interação entre
essa corrente e o campo magnético gerado
pelo imã.
Mudando-se a polaridade da corrente, muda o
sentido do movimento do ponteiro
O instrumento lê valor médio (numa rede AC
senoidal o resultado é zero), portanto serve
para medir sinais contínuos no tempo.
O que acontece ao medir CA com este
galvanômetro?
B bi Móvel
Bobina
Mó l e Retificadores
R tifi d
Apesar do galvanômetro do tipo bobina móvel ler apenas sinais DC, é possível
a utilização do mesmo nas medidas de sinais AC. Isto é normalmente feito com
a utilização de semicondutores retificadores (diodos)
Instrumento de D'ARSONVAL
O instrumento de D'Arsonval indica corrente em
uma direção apenas.
Sem um retificador,, ou corrente DC de
polaridade errada pode danificar o instrumento.
Uma vez que o ponteiro oscila em tornod e um
valor, uma mola de amortecimento deve ser
utilizada.
utilizada
Voltímetro
o t et o
A partir do Galvanômetro, basta adicionar uma
resistência em série.
Ideal Ri=∝ Ω
PS: O galvanômetro está em série com a resistência Rm
que representa a resistência do enrolamento. O limite de
corrente é dado pela capacidade do galvanômetro
V ltí t
Voltímetro
Ligação em paralelo
E ê i C
Essência:
Calcular
l l um resistor
i t em série
éi
para determinar a corrente de fundo de
escala do galvanômetro
Todo Instrumento apresenta uma Ri
Pode se calcular a queda de tensão pela lei de Ohm
Pode-se
A resistência interna do voltímetro é um parâmetro importante. Quanto
mais elevada, mais próximo do ideal o instrumento será e menor a
corrente que precisará para deslocar o ponteiro. Assim, a sensibilidade
d instrumento
do
i
é dada
d d pelo
l inverso
i
d
da corrente d
de fundo
f d d
de escala.
l N
Na
prática, na frontal dos instrumentos existe uma indicação em Ω/V, as
quais são as unidades de 1/IFE.
R
V
I
Ri
Galvanômetro
V − Ri I max
R=
I max
considere 3 voltímetros de diferentes sensibilidades:
100 Ω/V, 1000 Ω/V e 20000 Ω/V. Determine o
efeito
f it da
d resistência
i tê i interna
i t
na tensão
t ã lida
lid em cada
d
um dos casos quando ligados como na Figura.
Amperímetro
A partir do Galvanômetro
Galvanômetro, basta adicionar uma
resistência em paralelo.
Ideal Ri=0 Ω
O amperímetro deve ser conectado em série com o circuito
que deseja-se fazer a medida
Amperímetro
A Ligação em série deste instrumento provocará um curto
circuito.
Essência: Calcular um resistor em paralelo (resistor de shunt),
responsável pelo desvio da corrente de entrada
entrada, de modo que
pelo galvanômetro passe apenas a corrente de fundo de
escala.
Oh í t
Ohmímetro
Ap
partir do Galvanômetro, basta adicionar uma
bateria em série. A resistência a ser medida fecha o circuito.
Observe que você NÃO PODE ligar o ohmímetro em um circuito energizado
Utiliza escala não linear – zero - infinito.
Calibrar antes de sua utilização.
Checar 0Ω com as ponteiras em curto circuitoe
Não coloque o dedo (ou feche o circuito pelo corpo).
NÃO PODE!!!!
E
Exercício
í i
Dado um galvanômetro de 1 mA
Ri=60 Ω, deseja-se medir 220 V.
Qual o valor de R a se colocar em
série?
Calcule os valores das resistências do
Voltímetro
A
Ri
1000V
R1
500V
R2
100V
R3
50V
R4
10V
R5
5V
R6
Calcule os valores das resistências do
Voltímetro
A
Ri
5V
R1
10V
R2
50V
100V
500V
1000V
R3
R4
R5
R6
Resistência Interna
Para um instrumento com I= 1 mA
1
Ri =
= 1000 Ω
V
0, 001
Exercício: Considere uma fonte de 600 V R=10 KΩ e
3 voltímetros com as seguintes Ri:
A)
Ri = 100 Ω
V
B)
Ri = 1000 Ω
V
C)
Ri = 2000 Ω
V
Qual dos instrum. Fará a leitura mais fiel?
Amperímetro
Utiliza-se o mesmo galvanômetro
Utiliza-se uma resistência
ê
em paralelo com o
galvanômetro chamada R de shunt
R
I2-i1
A
i1
I2
Ri
Ex:: Com
Co um
u galvanômetro
ga va ô et o
de I=1mA e Ri=15 Ω,
Calcule R para fazer uma
medida de 8 A
Exercícios
Calcule R1 a
R6 para o
seguinte
amperímetro
p
A
Ri
R1
R2
R3
Ri=15 Ohms
A=1 mA
600 mA
1A
10 A
R4
20 A
R5
50 A
R6
65 A
Exercícios
Ri=15 Ohms
A 1 mA
A=1
Ri
5A
R1
10 A
A
R2
0
R3
R4
Calcule R1 a R4
no amperímetro ao
lado
1A
500 mA
Si b l i
Simbologia
Paralaxe
Quando a vista do observador
observador, a ponta do ponteiro e o
valor indicado na escala não se situam no mesmo
plano
Esta é a razão de se utilizar espelhos
p
no fundo da escala
Medição de Potência
O wattímetro
í
é um instrumento
i
capaz de
d realizar
li
a medida
did
da potência de consumo (potência útil) de uma carga
Cargas
g R,, L,, C em cisrcuitos AC.
Fator de Potência (cos Φ)
O wattímetro indica a potência útil !
Fatores de Potência muito baixos podem gerar correntes
altas no instrumento
Existem grandes diferenças na medição de potência em circuitos DC e AC. No
primeiro, o produto simples do valor da tensão pelo valor da corrente fornece a
potência elétrica consumida por uma carga ou fornecida por uma ou mais
fontes. Entretanto, em se tratando de circuitos AC, é preciso levar em conta a
fase de I e V
Medição de Potência
O fluxo de energia em uma resistência é sempre em um sentido, variando de
um valor mínimo de zero a um valor máximo duas vezes em cada ciclo.
Os capacitores e indutores também são conhecidos como elementos de
armazenagem de energia. O capacitor armazena energia na forma de campo
elétrico,
lét i
enquanto
t que o capacitor
it armazena energia
i na fforma de
d campo
magnético. A principal diferença destes dois elementos em relação ao resistor é
que este dissipa energia, enquanto que o L e C apenas armazenam. Desta
forma em um circuito excitado por uma fonte que varia a polaridade
forma,
polaridade, estes
elementos carregam e descarregam, de modo que a energia oscile entre fonte
e elementos LC ou entre elementos LC apenas.
Medição de Potência
Para facilitar a ligação, você pode pensar o wattímetro como dois instrumentos
separados: Um voltímetro – bobinas de tensão, e um amperímetro – bobinas
de corrente. A primeira deve ser ligada em paralelo e a segunda em série.
Preste atenção nos laboratório!!!!!
Observe que com o wattímetro, um voltímetro e um amperímetro, você poderá
medir o ângulo de defasagem entre a corrente e a tensão, e
consequentemente o FP do circuito
circuito.
Multímetros Digitais
g
(DMM)
(
)
DMMs são geralmente menores e
podem fornecer medidas com menor
p
incerteza.
Medidores analógicos, são mais
interessantes quando estamos
interessantes,
interessados em transientes.
Os DMMs, por serem em essência,
um processador
d di
digital
it l com um
conversor AD, os mesmos possuem
flexibilidade. Assim, muitos outros
medidores
did
são
ã iintegrados,
t
d
como:
testadores de diodos, de
transistores, medidores de
capacitância,medidores
â
de
temperatura, entre outros
Multímetros Digitais
g
(DMM)
(
)
A resolução dos instrumentos digitais é fornecida em função do número de dígitos.
Se um determinado instrumento mostrar uma grandeza com 999, diz-se que a mesma
é representada
p
p
por 3 dígitos.
g
Displays LCDs regulares representam as grandezas com um fundo de escala do tipo
1999 (2000 contagens) - neste caso diz-se que este instrumento é 3 e ½ dígitos.
Caso o fundo de escala seja 19999 (20000 contagens), diz-se que este instrumento é
4 e ½ dígitos.
g
Estes instrumentos tem os fundos de escala em múltiplos de 2 unidades (20 mA, 200
mA, 2 V, 20 V, 200 V , etc)
Existem ainda instrumentos que ao invés de possuírem fundos de escala 2 (unidade)
tem outros números – geralmente 4. Nestes casos diz-se
diz se que o instrumento tem n ¾
dígitos.
Observe que o número de dígitos do instrumento também define a resolução do
mesmo, uma vez que o dígito mais a direita representa menor variação lida por este
instrumento. Porém a composição
p ç da incerteza p
possui outros fatores
Dígitos
Contagens
Total
3 e 1/2
0 1999
0-1999
2000
3 e 3/4
0-3999
4000
4 e 1/2
0-19999
20000
4 e 3/4
0-39999
40000
4 e 4/5
0-49999
50000
Multímetros Digitais
g
(DMM)
(
)
Multímetros digitais utilizam conversores AD.
Atualmente são utilizados poderosos
microprocessadores, que entre outros recursos,
possuem conversores AD.
Os dígitos são geralmente feitos com LCD
(dysplay de cristal líquido) ou então displays
feitos com LEDs.
Muitos instrumentos (principalmente os de baixo
custo), são construídos a partir de um único
conversor AD como o 7106
7106, o qual já possui
decodificador para o display (ou o seu
equivalente para displays de LAD - 7107).
Isso facilita a construção pois são necessárias
apenas algumas ligações.
Também pode-se usar um simples
microcontrolador para implementar um voltímetro
por exemplo.
Características de conversores AD
O campo da eletrônica pode ser dividido em duas grandes áreas: analógico e digital.
Resumidamente pode-se citar algumas
g
características próprias das duas áreas:
Analógico: variável contínua. Por exemplo, tensão elétrica;
Digital: variável discreta. Por exemplo, uma seqüência de números (amostras)
representando uma tensão elétrica.
Características de conversores AD
Os detalhes de funcionamento destes dispositivos, não
são o foco principal deste curso. No entanto, sugerese ler
l a bibli
bibliografia
fi recomendada
d d para ver titipos e
características individuais dos conversores AD.
Função: Amostragem do sinal analógico
O conversor A/D
Dados digitais estão baseados em níveis de
sinais que se restringem a dois estados, ou seja, os
valores
l
“bi á i ” representados
“binários”
t d
pelos
l
valores
l
0 e
1. Estes níveis binários 0 e 1, são conhecidos como
“bits” e um g
grupo
p de bits recebe o nome de
“palavra” . Assim, uma palavra poderia ser 0101,
palavra que contém 4 bits. A posição dos bits na
palavra tem o significado de que o bit menos
significativo (LSB) é o último da direita e o bit mais
signficativo (MSB) está mais à esquerda da palavra.
O valor dos bits numa palavra é:
N 1...2
2N-1
24 23 22 21 20
MSB
LSB
Características de conversores AD
Algumas das principais
características de
conversores AD:
Faixa de entrada
Resolução e Número de
bits.
bits
Taxa de amostragem
linearidade
Entre outras, são
fundamentais para o projeto
do instrumento. No caso dos
multímetros, é necessário
precisão de medida
medida, porém a
velocidade ou taxa de
amostragem não precisa ser
elevada (o olho humano é
lento!) O tipo de conversor
lento!).
utilizado no 7107 ou 7106 é
DUPLA RAMPA (veja
bibliografia para maiores
detalhes) o qual encaixa
detalhes),
encaixa-se
se
nessas necessidades.
Uma palavra de 4 bits tem 24 níveis, ou seja, 16 níveis
Com a conversão de 4 bits, o menor sinal de entrada que
produzirá uma mudança na saída binária é 0,1V. Isso é
conhecido como resolução do conversor (na verdade, existem
outros fatores que podem afetar a resolução). Uma mudança
menor que 0,1V
0 1V na entrada
d não
ã produzirá
d i á nenhuma
h
mudança
d
na saída digital. A resolução de um conversor AD com N
bitspode ser calculada por:
R =
V en trada _ m ax − V entrada _ m in
2N −1
N é o número de bits do conversor A/D.
Um conversor de 8 bits tem sua escala dividida em 28 = 256
partes Assim
partes.
Assim, caso um conversor tenha uma escala de 10V (ou
seja, funda de escala 10V), a menor tensão que ele consegue
ler é 10V/256partes ≅ 0,04 V ≅ 40 mV.
Com 12 bits,
bits a menor tensão q
que
e ele conseg
consegue
e ler é 10V/212 ≅
10V/4096 ≅ 0,0025V ≅ 2,5 mV
O te
tempo
po de co
conversão
e são é ut
utilizado
ado pa
para
a espec
especificar
ca o
tempo que tarda o conversor em gerar uma palavra
digital, quando é jogado um sinal analógico na
entrada.
Caso forem utilizados conversores AD com
f üê i
freqüências
d amostragens
de
t
mais
i baixas
b i
que a
freqüência das componentes do sinal, ocorrerá o
problema de aliasing.
aliasing
Características de conversores AD
A faixa de entrada e o número de bits do conversor AD, podem determinar
a necessidade da construção
ç de um condicionador de sinais.
Você tem um equipamento que tem uma saída de 0 a 200 mV que indica
força de -500 a 500 Kgf (compressão e tração). Calcule a resolução desta
medida (em Kgf) se a mesma for ligada a uma placa AD de 8 bits com uma
escala de:
Você tem um equipamento que tem uma saída de 0 a 100 mV que indica
pressão de 0 a 100 mm Hg
p
g ((tor).
) Calcule a resolução
ç desta medida ((em
mm Hg ou Tor) se a mesma for ligada a uma placa AD de 8 bits com uma
escala de:
–500 mV a + 500 mV:
–1 V a + 1 V:
–5 a 5 V:
Repita o problema anterior para um conversor de 10 e 12 bits
respectivamente.
Como foi falado anteriormente,, esta aula não visa estudar os detalhes dos
tipos de conversores AD, bem como os detalhes de suas características.
Haverá uma disciplina no curso com esse objetivo. No entanto, reforço o
que foi dito, encorajando-o a ler os capítulos 3 e 4 do vol. 1 do livro texto.
Incerteza nos instrumentos digitais
Um indicador digital proporciona uma leitura numérica que elimina
o erro do
d operador
d em termos d
de iinterpolação
l ã e paralaxe;
l
Os valores lidos normalmente são expressos geralmente entre 3 ½
e 8 ½ dígitos;
g
;
A resolução desses instrumentos é correspondente à mudança de
tensão que faz variar o bit menos significativo no display do
medidor;
A incerteza é uma combinação de fatores dado em uma
percentagem e um número de bits, o qual indica quantas casas de
incerteza podem “flutuar” o dígito menos significativo (LSB).
Incerteza=(%leitura)+(dígitos)
Para faixa de 20 V:
Incerteza DMM
Incerteza
ce te a DMM
Baseline uncertainty
Como já observado anteriormente usualmente dada como ± (percent da leitura + número
de dígitos) ou ± (percent da leitura + número de contagens).
contagens)
“Digits” ou “counts” são usados como sinônimos e indicam o valor dos dígitos menos
significativos para uma faixa em particular.
Eles representam a resolução do DMM para essa faixa.
faixa
Se a faixa é 40,0000 então um dígito, uma contagem, é 0,0001.
Exemplo: queremos medir 10 V na escala de 20 V, na qual o dígito menos significativo
representa 0.0001 V.
Se a incerteza para a faixa de 20 V é dada como ± (0.003 % + 2 counts), então a
incerteza da medida será ± ((0.003 % x 10 V + 2 x 0.0001V) = ± (0.0003 V + 0.0002 V) =±
(0.0005 V) ou ± 0.5 mV
Alguns fabricantes usam a forma: ± (percent of reading + percent of range)
Nesse caso basta multiplicar a leitura (máxima) pela faixa e pela percentagem para obter
o segundo termo.
Em ambos os caso o segundo termo é denominado de “the floor”.
Esse termo considera os efeitos de offsets e ruído associados com uma faixa , assim
como aqueles comuns a todas as faixas.
Ignorar esse termo pode ter consequências significantes, especialmente para medidas
próximas do início da faixa.
Incerteza
ce te a DMM
Uncertainty modifiers
Modificadores podem ser aplicados a procedimentos para cálculo da incerteza para
contabilizar fatores ambientais ou temporais.
temporais
Algumas especificações podem conter recomendações para um período de tempo,
digamos 90 dias, ou um ano depois da calibração.
Isso determina que o DMM seja calibrado com mais frequência para certas aplicações.
aplicações
A incerteza também pode ser especificada para uma faixa de temperatura.
Usualmente a “temperatura ambiente”, é considerada de 18 °C a 28 °C (64.4 °F a 82.4 °F)
quando calibrado a 23 °C.
C.
A incerteza pode ser modificada pela temperatura
Digamos que queremos a mesma medida de 10 V anterior na mesma faixa, em campo,
onde a temperatura
p
é 41 °C ((106 °F).
)
O coeficiente de temperatura do DMM é dado por: ± (0.001 % da leitura) por °C de 0 °C a
18 °C e 28 °C a 50 °C.
A temperatura está a 13 °C acima dos 28 °C. Para cada grau acima do limite , temos que
adicionar 0.001 % x 10 V = 0.1 mV/°C a incerteza base.
A incerteza adicionada a 41 °C é 13 °C x 0.1 mV/°C = 1.3 mV. Assim, a incerteza total
combinando a incerteza base e a temperatura modificante será de ± (0.5 mV + 1.3 mV) =
± 1.8
1 8 mV.
V
Note que a incerteza modificada é mais que três vezes a incerteza base!
Incerteza DMM
Qualifier specifications
A incertezas do DMM dependem de outras condições além do tempo e da incerteza.
Fatores ambientais como temperatura de armazenamento, umidade, densidade do ar,
radiação eletromagnética podem afetar a incerteza.
O DMM deve receber enegia “limpa” para que seus circuitos e fontes internas funcionem
apropriadamente.
Al
Alguns
qualificadores
lifi d
podem
d
ser especificados
ifi d por valores
l
numéricos
éi
como regulaçào
l à
das linhas de energia, altitude e umidade relativa.
DMMs não são fechados hermeticamente e assim, o ar torna-se um componente que
pode influenciar nos resultados.
resultados
As caracterísiticas do ar são afetadas pela densidade (altitude) e umidade e em alguns
casos são dadas limitações baseadas nesses parâmetros.
Temperaturas excessivas de armazenamento podem alterar as características de
operação dos componentes eletrônicos.
Qualificadores mais complexos como proteção de sobretensão, choques mecânicos,
vibração ou compatibilidade eletromagnética são dados baseados em calibração e
limites.
Padrões Internacionais para essas características tipicamente requerem uma série de
procedimentos de teste ao longo de limites aplicáveis.
Adicionando todos os limites renderiam ao DMM especificações muito complicadas,
assim os projetistats de DMM apenas listam os padrões com os quais o DMM deve ser
comparado.
Considere o instr
instrumento
mento Tektronix
Tektroni TEKDMM 155
155, ccujas
jas especificações estão na
tabela abaixo.
Escala de resistência - 200Ω
Escala de tensão DC 20V
Escala de corrente DC 200mA
±1.2% da leitura + 2 dígitos
±0.7% da leitura + 2 dígitos
±1.2% da leitura + 2 dígitos
Considere a escala de resistência - 200Ω, Escala de tensão DC 20V e Escala de
corrente DC Para efetuar o cálculo da incerteza relativa ao instrumento e a sua
escala proceda calculando o erro quadrático dos parâmetros fornecidos:
onde n dígitos significam a variação de n unidades no dígito menos significativo
(mais a direita).
exemplo: escala de 200Ω com o ohmímetro medindo 100Ω, o visor do instrumento
mostra 100,0Ω (pois este é um instrumento 3 e ½ dígitos). Neste caso:
Exemplo:
p o multímetro Metex M4600(B).
( ) Esse instrumento, na escala de 20VDC
tem a incerteza = 0,05% da leitura + 3 dígitos. Calcule a incerteza de uma leitura
de 100,00 mV
Sempre
p é importante
p
consultar o manual do fabricante,, p
porque
q o erro combinado
pode mudar em função da escala ou do tipo de variável a ser medida.
Osciloscópio
p analógico
g
Os osciloscópios analógicos funcionam a partir de um TRC;. O canhão de elétrons (raios catódicos),
que emite elétrons na forma de um feixe, consiste de um aquecedor (filamento aquecido) um
cátodo uma grade de controle
cátodo,
controle, um ânodo de foco e um ânodo para acelerar os elétrons
elétrons. O conjunto
do TRC é também conhecido com válvula elétrica.
O filamento é uma resistência elétrica, geralmente alimentada com uma tensão AC baixa,
responsável pelo aquecimento do catodo que o encobre.
O cátodo é responsável
p
p
pela emissão de elétrons. Consiste num cilindro metálico recoberto com
óxidos que quando aquecido pelo filamento e excitado por uma diferença de potencial (negativo)
torna-se a fonte de elétrons que formarão o feixe.
A grade de controle tem por função regular a passagem de elétrons do cátodo para o anodo.
Consiste de um cilindro circular com um orifício circular. Possui o mesmo potencial que o anodo e
quando é controlado,
controlado ocorre uma variação no brilho do feixe visto na tela
tela.
O anodo de foco e o anodo de aceleração são elementos em forma cilíndrica com pequenos
orifícios que possuem alto potencial positivo em relação ao cátodo. Desta forma o feixe de elétrons
é acelerado e mantido coeso. Esta etapa também é conhecida como lente eletrônica por aplicar ao
feixe de elétrons um processamento semelhante ao fenômeno que ocorre em uma lente óptica.
A placas
As
l
de
d deflexão
d fl ã horizontal
h i
t l e vertical
ti l são
ã os di
dispositivos
iti
responsáveis
á i pela
l movimentação
i
t ã
do feixe de elétrons. Estas placas tornam possível a excursão de um (ou mais – dependendo do
tipo de osciloscópio) sinal por qualquer ponto da tela.
Osciloscópio
p analógico
g
As placas de deflexão do feixe são responsáveis pelos deslocamentos do
mesmo em x e y da tela.
A tela fosforescente é o dispositivo onde o feixe choca-se e tem como
resultado a liberação de energia em forma de luz.
O controle da base tempo consiste num circuito capaz de executar a
excursão do feixe de elétros da borda esquerda da tela até a borda direita em
um tempo precisamente constante. Isto permite que o usuário meça qualquer
qualquer parâmetro dependente do tempo. Para facilitar esta medida, a tela
está subdividida em n divisões (geralmente 8) de modo que o controle da
b
base
d
de ttempo permite
it ao usuário
á i escolher
lh uma b
base d
de ttempo adequada.
d
d
O controle de amplitude do osciloscópio é formado por um circuito
eletrônico que tem a função de adequar as intensidades dos sinais de
entrada.
Osciloscópio
p analógico
g
O controle da base tempo
p
Osciloscópio
p Digital
g
Os osciloscópios digitais têm seus princípios de
funcionamento bastante diferentes do analógico uma vez
que os sinais
i i são
ã amostrados
t d e adquiridos
d i id por um sistema
i t
de aquisição de dados que trabalha em altas velocidades.
Os mesmos podem utilizar ou não o TRC: se utilizarem o
TRC, as principais diferenças ficam por conta do poder de
armazenamento
t de
d dados
d d e possibilidade
ibilid d d
de ttratamento
t
t
dos mesmos. As funções oferecidas por osciloscópios
digitais dependem do modelo e do fabricante. Entre
algumas destas funções pode-se citar:
Visualização continua de sinais de baixa freqüência
Possibilidade de congelamento de telas
Possibilidade de programação de modo de disparo de
telas (trigger)
Programação do modo de visualização de parâmetros
(VRMS, VMÉDIA, Freqüência, Tempo,etc)
Auto-ajuste de canais
Possibilidade de ligar
g o instrumento em rede ((GPIB))
Dispositivos de interface como discos flexíveis
Recursos para medição precisa nas ordenadas e nas
abcissas – como barras móveis que permitem o
posicionamento
pos
co a e oe
exato
a o do inicio
c o e fim de trecho
ec o de
interesse do sinal.
Zoom
Outros
Osciloscópios
p
Ponteiras
Tarefa – extra aula
Existem muitos outros instrumentos para medição de grandezas
elétricas que não serão abordados em aula
aula. Faça uma pesquisa sobre
os seguintes instrumentos:
Medidor de capacitância
Medidor de indutância
Medidor de resistências muito baixas (impossível de medir com o
multímetro)
Medidor de resistências elevadas (megômetro)
Medidores de energia elétrica
Medidores de potência (ativa e reativa)
Pontes resistivas
Faça um estudo sobre o princípio de funcionamento e procure
circuitos de implementações dos instrumentos:
Bibli
Bibliografia
fi
HOLMAN J. P. Experimental Methods for
Engineers,.McGraw-Hill, Inc
DOEBELIN,, O. Measurement Systems,
y
,
McGraw-Hill, 1990.
BALBINOT A.,
A BRUSAMARELLO V.
V J.,
J
Instrumentação e Fundamentos de Medidas V
1 e V2 , 2006 e 2007
2007.