1. A corrente

IST/DEEC
LEEC
Exame de Análise de Circuitos
26 de Junho de 2006
Número
2º Semestre 2005/2006
Duração: 2 horas
Sala
Nome
Das respostas às perguntas 1 a 7 (inclusive) apenas serão cotadas as assinaladas na
tabela abaixo e a cada resposta ERRADA desconta-se 25% da respectiva cotação!
Alínea
1
2
3
4
Cotação
1
C
1
B
1
A
1
A
5
6
7
8a
8b
8c
9a
9b
9c
10a
10b
10c
1
1
1
2,0
2,0
1,0
1,0
1,0
2,0
1,0
2,0
1,0
D B B
Afixação de Pautas 3 de Julho de 2006 às 15h00.
Revisão de Provas: 4 de Julho às 15h00 (J. Costa Freire) e 5 de Julho às 9h00 (Teresa Almeida).
RESPOSTA
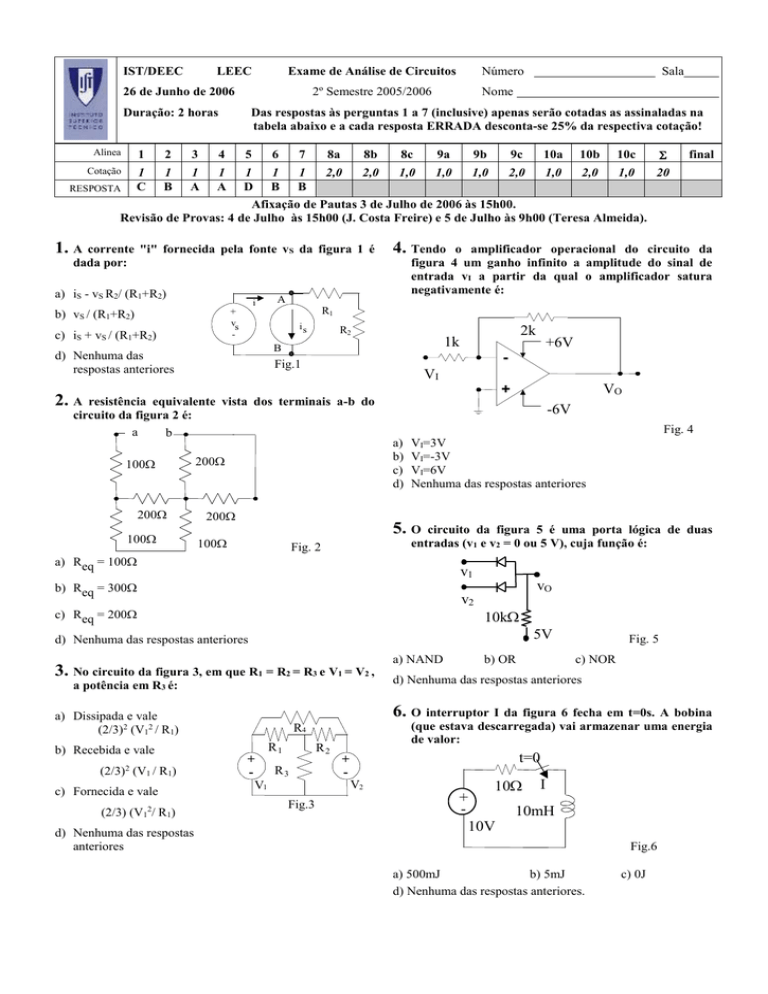
1. A corrente "i" fornecida
pela fonte vS da figura 1 é
i
o amplificador operacional do circuito da
figura 4 um ganho infinito a amplitude do sinal de
entrada vI a partir da qual o amplificador satura
negativamente é:
A
R1
+
vs
-
b) vS / (R1+R2)
c) iS + vS / (R1+R2)
is
R2
2k
1k
B
d) Nenhuma das
respostas anteriores
+6V
-
Fig.1
VI
+
2. A
VO
resistência equivalente vista dos terminais a-b do
circuito da figura 2 é:
a
b
100
200
100
-6V
Fig. 4
a)
b)
c)
d)
200
200
VI=3V
VI=-3V
VI=6V
Nenhuma das respostas anteriores
5. O
100
circuito da figura 5 é uma porta lógica de duas
entradas (v1 e v2 = 0 ou 5 V), cuja função é:
Fig. 2
a) Req = 100
v1
vO
b) Req = 300
v2
c) Req = 200
10k
5V
d) Nenhuma das respostas anteriores
3. No circuito da figura 3, em que R1 = R2 = R3 e V1 = V2 ,
a potência em R3 é:
(2/3)2 (V1 / R1)
c) Fornecida e vale
(2/3) (V12/ R1)
d) Nenhuma das respostas
anteriores
a) NAND
b) OR
Fig. 5
c) NOR
d) Nenhuma das respostas anteriores
6. O interruptor I da figura 6 fecha em t=0s. A bobina
a) Dissipada e vale
(2/3)2 (V12 / R1)
b) Recebida e vale
final
4. Tendo
dada por:
a) iS - vS R2/ (R1+R2)

20
(que estava descarregada) vai armazenar uma energia
de valor:
R4
R1
+
R3
V1
Fig.3
R2
t=0
+
V2
10 I
+
10mH
10V
Fig.6
a) 500mJ
b) 5mJ
d) Nenhuma das respostas anteriores.
c) 0J
7. No circuito da figura 7 tem-se: i1 = 5A, iC = 10 cos t (A)
e vR = - 30 cos t (V). Qual o valor de vL?
a) Calcule a constante de tempo de carga ou descarga do
condensador C de 0 a t1.
Sol:  = 1 ms
iC
2F
b) Qual é valor da energia armazenada no condensador C no
instante t=9ms? Justifique a sua resposta.
Sol: t = 9 ms = 9  regime estacionário  vC = 7V 
WC = 24,5 J
+ vR -
i1
2
3
+
vL
-
4H
c) Obtenha as expressões de vc(t) e vx(t) para t < t1 e
represente-as graficamente.
Sol:t<0 - vc(t) = 4 (V); vx(t)= 0
t>0 - vc(t) = 7 – 3 e 1000t (V); vx(t)= 0,3 e 1000t (V)
iL
Fig. 7
a)
b)
c)
d)
0 (V)
– 80 sen t (V)
10 + 80 sen t (V)
Nenhuma das respostas anteriores
10.
Considere o circuito da figura 9 em t>t1, com o
gerador vI sinusoidal.
8. Considere
o circuito da figura 8, que tem dois
geradores independentes e um dependente.
d
E
+
-
R1
a
- vA +
c
+
Sol:
vA
10 9 s 2
10 8 s 2  91  10 5  1
b) Trace os diagramas assimptóticos de Bode (amplitude e
fase) da função
I v
R2
a) Calcule a função de transferência G(s) = Vl(s) / Vi (s) na
forma literal (função de R1, R2, C e L) como um
quociente de polinómios em s ordenados. Não necessita
de efectuar cálculos numéricos.
b
H(s) = Io(s) / Ii(s) =
E = 10 V, I = 7 A, R1 = 4, R2 = 2, α = 0.5
Fig. 8
60
a) Determine as tensões nodais va a vd , aplicando o método
nodal. Use para referência o nó ligado à terra. Comece por
escrever a equação matricial literal (simbólica) e só efectue
cálculos numéricos depois.
40
0
 0

Sol:  1  
1
 1/ R1 1/ R2
  va   E 
   vc    0  ; va=-2V; vd=10V
 1/ R1  vd   I 
c) Calcule as potências postas em jogo nas fontes E e I. Elas
são fornecidas ou absorvidas pelas fontes?
Sol: PE = -30 W fornece; PI=-14 W fornece
9. Considere o circuito da figura 9, onde o interruptor T
só fecha em t=t1. Sabe-se que o gerador vI=4V para t<0
e vI=7V para t>0.
iC
vI +-
+ vC R1
C
t1
R2
+
vX
-
T
L
+
vL
-
R1 = 900, R2 = 100, C = 1F, L = 1mH, t1 = 10ms
Fig. 9
dB
20
0
1
b) Calcule as correntes de circulação nas malhas, i1 e i2, com
o sentido dos ponteiros do relógio, aplicando o princípio da
sobreposição.
Sol: i1=5/4 + 7/4=3 A; i2=7 A
|H(j )|
10 3 s 2
10s  1,01  10 6 s  109
2
1
103
10
105 rads -1 ]
Sol:
[rad s -1 ]
H (j)
180º
1
90º
10
103
105

0º
c) Supondo iI (t) = 10 sen (104 t +
resposta forçada iO (t).
Sol: iO (t) = 1 sen (104 t +) (A)

) mA, calcule a
2