Quarta Aula Prática

CENTRO FEDERAL DE EDUCAÇÃO TECNOLÓGICA
UNIDADE BRAGANÇA PAULISTA
CURSO DE AUTOMAÇÃO INDUSTRIAL
Quarta Aula Prática
Objetivo;
1 – Comprovar experimentalmente a os Cálculos Conversão de circuitos Estrela e em
Triângulo , Conversão Triângulo em Estrela e a Equação de equilíbrio da Ponte de
Wheatstone.
Material utilizado;
- Bastidor de Sistema de Treinamento em Eletrônica Analógica (Bit9);
- Módulo com Prot. Board.
- Fonte de tensão fixa de 5v;
- Multímetro;
- Cabinhos de conexão.
- Resistores de valores diversos
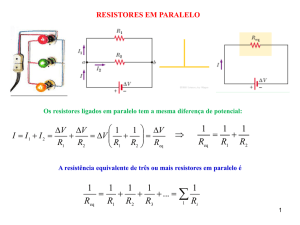
Introdução teórica
Conversão de Circuito Estrela ( Y ) em Triângulo (Δ)
Em algumas situações, torna-se necessário a conversão dos circuitos Y para Δ, para
facilitar análise elétrica do mesmo.
Para esta operação são utilizadas as equações aqui descritas:
Fig 1
Ra 
R1  R 2  R1  R3  R 2  R3
R1
Rb 
R1  R 2  R1  R3  R 2  R3
R2
Rc 
R1  R 2  R1  R3  R 2  R3
R3
Conversão de Circuito Triângulo em (Δ) Estrela ( Y )
Em algumas situações, torna-se necessário a conversão dos circuitos Y para Δ, para
facilitar análise elétrica do mesmo. Para esta operação são utilizadas as equações
aqui descritas:
Fig. 2
R1 
Rc  Rb
Ra  Rb  Rc
R2 
Ra  Rc
Ra  Rb  Rc
R3 
Ra  Rb
Ra  Rb  Rc
Para casos particulares onde os três resistores têm o mesmo valor, uma regra
facilita esta conversão.
R
R 
R  3R
3
Ponte de Whetstone
A Ponte de Wheatstone é um circuito muito utilizado em medidas elétricas, para obter
o valor de uma resistência desconhecida, a partir de um conjunto de outras já
conhecidas e tomadas como padrão (figura 3). Geralmente duas resistências são
fixas, uma é ajustável e a quarta é a incógnita que se pretende determinar.
Fig. 3
i1 
Vou = Va – Vb = -i2R1 + i1 R3
Logo:
V
V
out

s
R
3
R3  R4

Vs
R3  R4
i2 
e
Vs
R1  R2
R
1
R1  R2
Eq1
Se introduzirmos um Galvanômetro ( Voltímetro no nosso caso) entre os terminais AB,
podemos determinar o ponto de equilíbrio da ponte, isto é, quando a corrente IG no
ramo AB é nula. Quando IG = 0 Vout = 0 neste caso a equação 1 fica
0
R
3
R3  R4

R
1
R1  R2
R
3
R3  R4

R
1
R1  R2
RR
1
4

RR
2
3
Eq2
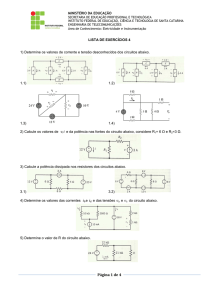
Parte experimental
1 – Escolha seis resistores, anote seus valores no quadro 1, calcule o Req de a cordo
com a figura 4,
Fig. 4
Ra
Rb
Rc
Rd
Re
Rf
Req Calculada= _____________
2 – Monte o circuito no protoboard e com o auxilio do multímetro em escala ôhmica,
meça o valor de Req.
Req Medida = ________________
3 – Compare os valores e descreva se o método matemático é valido para
calculo da resistência equivalente em circuitos estrela - triângulo
4 – Com os resistores de 1kΩ, 4k7Ω o desconhecido e o potenciômetro monte o
circuito da figura 5.
Fig. 5
5 – Alimente o circuito com 5Vcc e com o auxilio do voltímetro, meça o valor de
Vab. Ajuste o Potenciômetro até que Vab seja igual a zero.
6 – Desligue a alimentação e com o ohmímetro meça o valor da resistência
entre o ponto central e o terminal ligado a Vab anote o valor no quadro abaixo
Resistência medida =
7 – Através da equação 2 determine o valor da resistência Rx, e após o calculo
meça o valor de RX com o ohmímetro e compare os valores
Valore medido
Rx
Valor Calculado
Rx
8 – Justifique se os valores encontrados validam a teoria apresentada.
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_____________________________________________________________________
_______________