Física - Etapa

Questão 46
Um garoto, brincando com seu “autorama”,
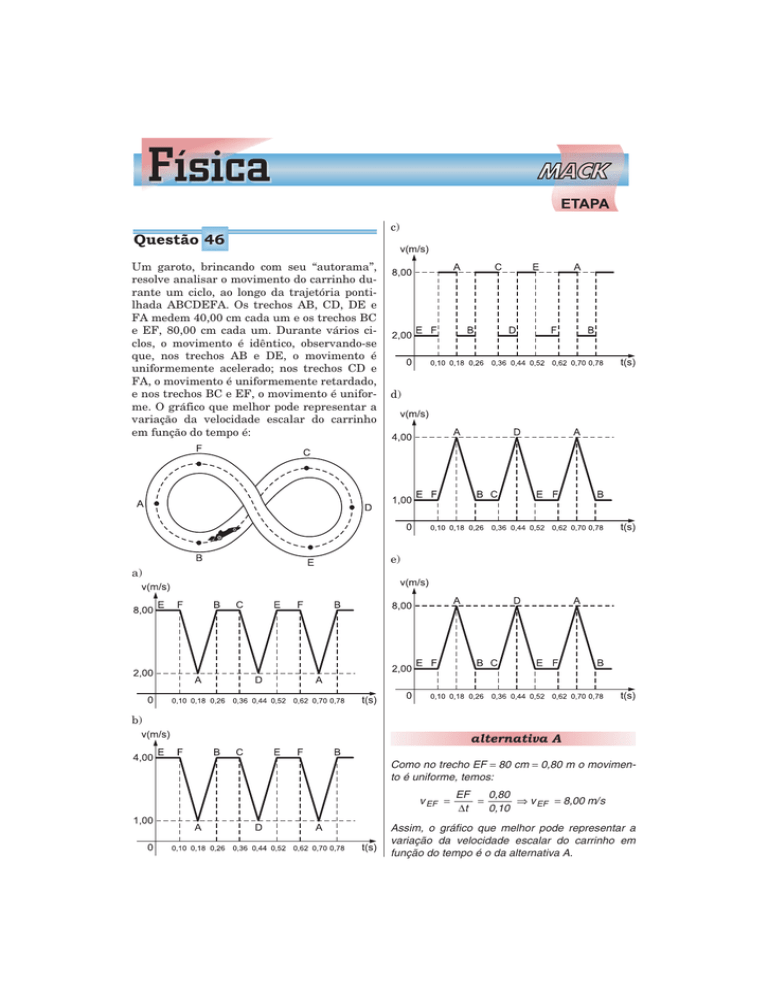
resolve analisar o movimento do carrinho durante um ciclo, ao longo da trajetória pontilhada ABCDEFA. Os trechos AB, CD, DE e
FA medem 40,00 cm cada um e os trechos BC
e EF, 80,00 cm cada um. Durante vários ciclos, o movimento é idêntico, observando-se
que, nos trechos AB e DE, o movimento é
uniformemente acelerado; nos trechos CD e
FA, o movimento é uniformemente retardado,
e nos trechos BC e EF, o movimento é uniforme. O gráfico que melhor pode representar a
variação da velocidade escalar do carrinho
em função do tempo é:
c)
d)
e)
a)
b)
alternativa A
Como no trecho EF = 80 cm = 0,80 m o movimento é uniforme, temos:
v EF =
EF
0,80
=
⇒ v EF = 8,00 m/s
∆t
0,10
Assim, o gráfico que melhor pode representar a
variação da velocidade escalar do carrinho em
função do tempo é o da alternativa A.
física 2
alternativa D
Questão 47
Isolando os corpos e marcando as forças, vem:
Numa avenida retilínea, um carro encontra-se parado em um semáforo; ao sinal verde, o carro parte com aceleração constante de
1,5 m/s2 , e, ao atingir a velocidade escalar de
27 km/h, a mantém constante por 2 s. A partir desse instante, o carro é freado uniformemente por 11,25 m, parando em outro semáforo. A velocidade escalar média desse carro,
no percurso descrito, foi de:
a) 2,5 m/s
b) 3,0 m/s
c) 3,5 m/s
d) 4,0 m/s
e) 4,5 m/s
alternativa E
No primeiro trecho, o carro realiza um MUV com
velocidade final v = 27 km/h = 7,5 m/s.
Da Equação de Torricelli, temos:
v12 = 0 2 + 2a ⋅ ∆S1 ⇒ 7,5 2 = 2 ⋅ 1,5 ⋅ ∆S1 ⇒
⇒ ∆S1 = 18,75 m
O intervalo de tempo (∆t1 ) é dado por:
∆S1
0 +v
18,75
7,5
=
⇒
=
⇒ ∆t1 = 5 s
∆t1
2
∆t1
2
No segundo trecho, o carro realiza um MU.
Assim, temos:
∆S 2 = v ⋅ ∆t 2 = 7,5 ⋅ 2 ⇒ ∆S 2 = 15 m
No terceiro trecho, o carro realiza um MUV até o
repouso. Assim, vem:
∆S 3
v +0
11,25
7,5
=
⇒
=
⇒ ∆t 3 = 3 s
∆t 3
2
∆t 3
2
Assim, a velocidade (v m ) escalar média no percurso total é dada por:
∆S1 + ∆S 2 + ∆S 3 18,75 + 15 + 11,25
⇒
=
vm =
5 +2 +3
∆t1 + ∆t 2 + ∆t 3
⇒
v m = 4,5 m/s
O sistema ao lado consiste
de polias e fios ideais. Os
corpos A e C têm massas
iguais a 3 kg cada um, e a
massa de B é 4 kg. Estando
o corpo B ligado, por fios,
aos corpos A e C, a aceleração com que ele sobe é de:
mC g − T = mC γ
⇒ mAg − mB g + mC g = (mA + mB + mC ) γ ⇒
⇒ 3 ⋅ 10 − 4 ⋅ 10 + 3 ⋅ 10 = (3 + 4 + 3) γ ⇒
⇒ γ = 2 m/s 2
Questão 49
Um pequeno corpo, de 100 g, é abandonado
do repouso, de um ponto A situado 10,0 m
acima do solo, plano e horizontal. Após chocar-se com o solo num ponto B, o corpo retorna segundo a mesma vertical BA, até parar
no ponto C. Se a resistência do ar é desprezada, o módulo da aceleração gravitacional local é g = 10 m/ s2 e o coeficiente de restitui-
alternativa B
A velocidade (v) com que o corpo atinge o solo é
dada por:
o
v 2 = v 02 + 2gh ⇒ v 2 = 2 ⋅ 10 ⋅ 10,0 ⇒
Adote:
g = 10 m/s2
b) 4 m/s2
e) 1 m/s2
2T − mB g = mB γ ⇒
ção no choque é 0,40, o módulo do trabalho
realizado pela força peso desse corpo, no trecho BC do movimento, é:
a) 0,80 J
b) 1,6 J
c) 2,0 J
d) 4,0 J
e) 8,0 J
Questão 48
a) 5 m/s2
d) 2 m/s2
Por simetria, temos T1 = T2 = T . Ao abandonarmos o sistema do repouso, temos que os blocos
A e C descem acelerando para baixo, enquanto o
bloco B sobe acelerando para cima.
Aplicando o Princípio Fundamental da Dinâmica
aos blocos, e somando-se as equações, vem:
mAg − T = mA γ
c) 3 m/s2
⇒ v = 10 2 m/s
Da definição de coeficiente de restituição, podemos calcular a velocidade (v’) com que o corpo
abandona o chão:
|v’ |
v’
e =
⇒ 0,40 =
⇒ |v ’| = 4 2 m/s
v
10 2
física 3
Aplicando-se o Teorema da Energia Cinética no
trecho BC, temos:
τ
= ∆EC ⇒ PτC
B =
τ
=−
C
R B
C
P B
0,1(4 2 ) 2
⇒
2
2
−
mv’
2
2
m 4,00
=
=
V
5,00
= 0,800 kg/l e a massa específica da água é
µ = 1,0 g/cm 3 = 1,0 kg/l.
No equilíbrio (R = 0), temos:
E = P ⇒ µVLDg = mg ⇒ 1,0 VLD = 4,00 ⇒
⇒ VLD = 4,00 l
Como o volume de líquido deslocado (VLD ) é igual
ao volume (Vi ) da parte imersa do paralelepípedo
e menor que 5,00 l, conclui-se que ele flutua e
sua massa imersa (mi ) será dada por:
m
mi
Vi = VLD ⇒ i = VLD ⇒
= 4,00 ⇒
0,800
d
A densidade do paralelepípedo é d =
0
mvC2
alternativa C
⇒
|P τC
B | = 1,6 J
Questão 50
Num relógio convencional, que funciona corretamente, o ponteiro dos minutos tem 1,00 cm
de comprimento e o das horas, 0,80 cm. Entre o
meio-dia e a meia-noite, a diferença entre o espaço percorrido pela ponta do ponteiro dos minutos e o espaço percorrido pela ponta do ponteiro das horas é aproximadamente igual a:
a) 35,2 cm
b) 70,3 cm
c) 75,4 cm
d) 140,8 cm
e) 145,4 cm
alternativa B
Adotando-se π = 3,14, em doze horas a ponta do
ponteiro dos minutos percorre uma distância (dM )
dada por:
dM =12 ⋅ 2 ⋅ π ⋅ RM ⇒ dM = 12 ⋅ 2 ⋅3,14 ⋅1,00 ⇒
⇒ dM = 75,36 cm
Já a ponta do ponteiro das horas, no mesmo intervalo de tempo, percorrerá uma distância (dH )
dada por:
dH = 2 ⋅ π ⋅ RH ⇒ dH = 2 ⋅ 3,14 ⋅ 0,80 ⇒
⇒ dH = 5,02 cm
Calculando a diferença pedida, temos:
dM − dH = 75,36 − 5,02 ⇒ dM − dH = 70,3 cm
Questão 51
Um paralelepípedo homogêneo, de massa
4,00 kg, tem volume igual a 5,00 litros. Quando colocado num tanque com água de massa
específica igual a 1,0 g/cm3 , esse paralelepípedo:
a) afunda.
b) flutua, ficando totalmente imerso.
c) flutua, e a massa da parte imersa é de
3,20 kg.
d) flutua, e a massa da parte imersa é de
3,00 kg.
e) flutua, e a massa da parte imersa é de
1,00 kg.
⇒
mi = 3,20 kg
Questão 52
Num laboratório, um aluno aquece de 50 o C
uma barra metálica de comprimento inicial
80 cm, observando que o seu comprimento
aumenta de 0,8 mm. Fazendo os cálculos, ele
conclui que o coeficiente de dilatação linear
do material da barra vale:
a) 5 ⋅ 10−5 oC−1
b) 4 ⋅ 10−5 oC−1
c) 3 ⋅ 10−5 oC−1
d) 2 ⋅ 10−5 oC−1
−5 o −1
e) 1 ⋅ 10
C
alternativa D
Sendo ∆L = 0,8 mm = 8 ⋅ 10 −2 cm, o coeficiente
de dilatação linear (α) é dado por:
∆L = L0 ⋅ α ⋅ ∆θ ⇒ 8 ⋅ 10 −2 = 80 ⋅ α ⋅ 50 ⇒
⇒
α = 2 ⋅ 10 −5 o C −1
Questão 53
Num laboratório, situado ao nível do mar,
massas iguais de água líquida e gelo (água
sólida) estão há um bom tempo em um recipiente de paredes adiabáticas e de capacidade térmica desprezível. Introduzindo-se 100 g
de água fervente nesse recipiente, verifica-se
que, após alguns minutos, se atinge o equilíbrio térmico do sistema, e que nele só existe
água líquida a 0 o C. A massa de gelo existente no recipiente, no início da experiência, era:
física 4
Dados:
calor específico da água sólida (gelo) =
= c g = 0,50 cal/(go C)
calor específico da água líquida = ca =
= 1,00 cal/(go C)
calor latente de fusão do gelo = Lf =
= 80 cal/g
calor latente de vaporização da água =
= Lv = 540 cal/g
a) 50 g
d) 100 g
b) 62,5 g
e) 125 g
c) 80,0 g
alternativa E
Sendo m a massa de gelo existente no recipiente
no início da experiência e sendo o equilíbrio a
0 oC , podemos concluir que ocorreu troca de calor
entre a água fervente e o gelo. Portanto, temos:
Qg + Qa = 0 ⇒ mLf + mac a ∆θ a = 0 ⇒
⇒ m ⋅ 80 + 100 ⋅ 1,00 ⋅ (0 − 100) = 0 ⇒
⇒
m = 125 g
Questão 54
Num recipiente, fechado por uma tampa hermética, há 10 mols de gás perfeito, sob pressão de 5 atmosferas, à temperatura ambiente
e em um local de pressão atmosférica normal.
Abrindo a tampa do recipiente, o número de
moléculas que escapa é:
Adote:
Número de Avogadro = 6.1023
a) 12.1023
d) 48.1023
b) 24.1023
e) 60.1023
c) 36.1023
alternativa D
Da equação de estado para um gás perfeito, sendo a temperatura e o volume constantes, vem:
n
V
pV = nRT ⇒
=
= constante
p
RT
Assim, para o gás que fica dentro do recipiente,
temos:
n
n’
10
n’
=
⇒
=
⇒ n ’ = 2 mols
p
p’
5
1
Portanto, o número de mols que escapam do recipiente é n − n ’ = 8 mols.
Sabendo-se que 1 mol de moléculas tem
6 ⋅ 10 23 moléculas, o número de moléculas que escapam é dado por 8 ⋅ 6 ⋅10 23 = 48 ⋅10 23 moléculas.
Questão 55
À frente de um espelho esférico côncavo, de
distância focal f, colocamos um pequeno objeto, a uma distância 3f do espelho. Obedecidas as condições de Gauss e aproximando
esse objeto do espelho até a distância 2f, a
distância de sua imagem ao espelho:
f
f
b) aumenta de .
a) diminui de .
2
2
c) diminui de f.
d) aumenta de f.
e) aumenta de 2f.
alternativa B
Pela equação de conjugação, para p = 3f , temos:
1
1
1
3
f
=
+
⇒ p’I =
f
3f
p’I
2
Para p = 2f , vem:
1
1
1
=
+
⇒ p’II = 2f
f
2f
p’II
Portanto a distância da imagem ao espelho auf
.
menta de p’II − p’I =
2
Questão 56
Num laboratório, são
realizadas experiências com dois pêndulos
simples distintos. O
primeiro, de comprimento L, denominado
pêndulo A, possui um
corpo suspenso de
massa m. O segundo,
de comprimento L/3,
denominado pêndulo
B, possui um corpo
suspenso de massa
3m. A relação entre os respectivos períodos de oscilação desses pêndulos é:
a) TA = TB ⋅ 3
b) TB = TA ⋅ 3
c) TA = TB
d) TA = 9 ⋅TB
e) TB = 9 ⋅TA
física 5
alternativa A
alternativa A
Para pequenas oscilações em pêndulo simples,
temos:
L
L
TA = 2 π
2π
g
g
TA
=
⇒
⇒
TB
L/3
L/3
π
2
TB = 2 π
g
g
Pela Lei de Coulomb, a força elétrica é inversamente proporcional ao quadrado da distância
entre as cargas, ou seja, para uma distância de
2 mm teremos uma força de intensidade F/4.
⇒ TA = TB ⋅ 3
Questão 57
Dois pequenos corpos, idênticos, estão eletrizados com cargas de 1,00 nC cada um. Quando estão à distância de 1,00 mm um do outro,
a intensidade da força de interação eletrostática entre eles é F. Fazendo-se variar a distância entre esses corpos, a intensidade da
força de interação eletrostática também varia. O gráfico que melhor representa a intensidade dessa força, em função da distância
entre os corpos, é:
a)
b)
Questão 58
Um corpúsculo dotado de carga elétrica negativa é abandonado, a partir do repouso, no
interior de um campo elétrico uniforme, gerado por duas placas metálicas, paralelas
entre si e carregadas com cargas iguais e de
sinais diferentes. O movimento adquirido
por esse corpúsculo, em relação às placas, é:
a) retilíneo e uniforme.
b) retilíneo uniformemente retardado.
c) retilíneo uniformemente acelerado.
d) circular uniforme.
e) acelerado com trajetória parabólica.
alternativa C
Como o campo elétrico é uniforme, a força que
atua sobre o corpúsculo é constante, ou seja, a
aceleração adquirida por ele também é constante.
Assim, o corpúsculo adquire um movimento uniformemente acelerado.
Questão 59
c)
d)
Um gerador elétrico, um receptor elétrico e
um resistor são associados, convenientemente, para constituir o circuito a seguir. O amperímetro A e o voltímetro V são ideais e,
nas condições em que foram inseridos no circuito, indicam, respectivamente:
e)
a) 83,3 mA e 3,0 V.
c) 375 mA e 13,5 V.
e) 75 mA e 2,7 V.
b) 375 mA e 0,96 V.
d) 75 mA e 0,48 V.
física 6
alternativa E
Aplicando a Lei de Ohm-Pouillet no sentido horário, vem:
40i − 3 = 0 ⇒ i = 0,075 A
Assim, a leitura do amperímetro é LA = i = 75 mA.
A leitura do voltímetro LV é dada por:
LV = Ri = 36 ⋅ 0,075 ⇒
b)
c)
LV = 2,7 V
Questão 60
Entre os ímãs A e B existe um campo de indução magnética uniforme, paralelo ao eixo
y, e os efeitos de borda são desprezados. Uma
carga elétrica puntiforme +q chega no ponto
O do sistema de eixos cartesianos, adotado
como referencial, com velocidade v de mesma
direção orientada pelo eixo z.
A trajetória descrita pela carga elétrica é a
curva OP, melhor representada na figura:
a)
d)
e)
alternativa C
O campo de indução magnética tem direção e
sentido coincidente com o eixo y e a velocidade
coincide com o eixo z. Assim, pela regra da mão
esquerda, a carga descreve uma trajetória circular
no plano xz , como indicado na alternativa C.