Vapor d´água e seus efeitos termodinâmicos

Capítulo 1
Vapor d´água e seus efeitos
termodinâmicos
Energia livre de Gibbs e Helmholtz
Equação de Clausius Clapeyron
Funções Termodinâmicas e condições
de equilíbrio
Em estados de equilíbrio (P,T e  são ctes) todas as
transformações de fase são possíveis e são
reversíveis ( a entropia não se altera)
Vapor
Vapor
Liquido






Liquido
Sólido
Sólido
A Entropia Aumenta neste Sentido 
Sólido
Liquido
Vapor
• Neste processo temos que qualquer aumento
em entropia de um corpo é igual em
magnitude à diminuição em entropia do
ambiente.
• Lembrando que a condição necessária para
um estado de equilíbrio é que a entropia total
de um corpo e do ambiente sejam ctes.
• Entretanto, esta condição de equilíbrio de
estado é muito difícil de ser aplicada em
prática durante as transformações de fase.
• Para entender melhor este processo
necessitamos avaliar duas funções de estado
termodinâmico que podem nos levar a
condições de equilíbrio sob certas condições:
 Energia Livre de Helmholtz
 Energia Livre de Gibbs
Energia Livre de Helmholtz - F
• A energia livre de Helmholtz, F, de um corpo
de massa unitária é expressa como:
F = u – TS
onde u é a energia interna, T a temperatura e S
a entropia do sistema
Analisando a variação de F (diferenciando) temos:
dF = du – TdS – SdT
lembrando que para um estado de equilíbrio em
um processo reversível podemos aplicar a 1º lei
da termodinâmica definida por:
dq  du  pd 
E Lembrando que a Entropia é  dS 
dq
T
Logo
TdS
 du  pd 
1º Lei
dF
 du  SdT
 Tds
dF
 Tds
dF
  pd   SdT
 pd   SdT
 Tds
dF
  SdT
 pd 
• Logo se um corpo estiver em equilíbrio e a sua
temperatura e volume forem constantes, temos
que:
dF = 0
• Por outro lado, se um corpo sofrer uma mudança
de fase espontânea (aumento a entropia) temos
uma transformação irreversível (pois a entropia
teria que diminuir!!), logo temos que:
dF < -SdT - pd ( ou dF < du – TdS – SdT)
• Se a transformação for isotérmica:
dF = du – TdS
• Se a transformação for espontânea e
irreversível com T e  constantes temos:
dF ≤ 0
Logo tanto a entropia (S) como a energia
interna (du) irão aumentar.
• Dessa maneira, em um estado de
equilíbrio com T e Vol constantes,
a energia livre de Helmholtz tem
um mínimo e por esta razão é
conhecida como potencial
termodinâmico com Vol e T cte.
Energia Livre de Gibbs - G
• A energia livre de Gibbs, G, de um corpo de
massa unitária pode ser expressa como:
G  u  TS  p 
Onde u é a energia interna, T a temperatura, p a
pressão e  o volume específico e S é a
entropia do sistema
Analisando a variação de G, temos:
dG  du  TdS
 SdT
 pd    dp
Logo a partir da 1º e da 2º lei da termodinâmica
e para um processo reversível, temos
TdS
 du  pd 
Logo, temos
dG  TdS
 TdS
dG   SdT
 SdT
  dp
  dp
• Portanto se T e P são constantes para
um corpo em equilíbrio, dG = 0
• Já para um corpo que sofre uma
transformação espontânea e
irreversível temos:
dG   SdT
  dp
onde dG ≤ 0
• O critério de equilíbrio termodinâmico
de um corpo com T e P constantes é
que a energia livre de Gibbs tenha um
valor mínimo.
• Portanto, a energia livre de Gibbs é
também conhecida como potencial
termodinâmico a pressão constante
• Ou
Energia associada a uma reação
química que pode ser usada para
realizar trabalho.
Equação de Clausius-Clapeyron
Equação do estado para o vapor d’água
• Diferentemente de outros constituintes
atmosféricos, a água aparece na atmosfera em
três fases: sólido, liquido e vapor.
• Na fase vapor, temos que o vapor d’água na
atmosfera se comporta aproximadamente
como um gás ideal
Neste sentido pode re-escrever a
equação do estado como:
e   v R vT
eq. (1)
onde e=pressão de vapor, v = densidade
do vapor, R v = é constante individual do
vapor d’água (461,5 J/kgK) e
T a temperatura
De uma outra forma
e  
R´
v

T
eq. (2)
onde =R’/ R v = m v /m = 0,622
Equação de Clausius-Clapeyron
Condensação
Evaporação
• Assumindo um ambiente fechado e
termicamente isolado
Equilíbrio - I
• O equilíbrio é alcançado quando as
taxas de condensação e evaporação
se tornam iguais.
• Logo a temperatura do ar e a do
vapor se igualam a do liquido e não
existe mais um saldo resultante
entre as fases.
Equilíbrio - II
• Quando isso ocorre, dizemos que
o ar acima do liquido está
saturado com vapor d’água.
Portanto a pressão parcial sob
estas condições é definida como
pressão de vapor de saturação.
Nuvem na Garrafa
Condensação
Evaporação
• https://www.youtube.com/watch?v=YUdR9xESD64
Pressão de Vapor de Saturação
• Conhecida também como eq. de
Clausius Clapeyron – C.C.
• Pressão de saturação entre as s
interfaces
–Vapor  liquido (condensação)
–Vapor  sólido (sublimação)
–Liquido  Sólido (congelamento)
• Durante as transições de fase, é
necessário energia (calor) para
sobrepor a energia cinética de
algumas moléculas, por exemplo
vapor liquido,
vapor  sólido e
liquido  sólido.
Para converter uma unidade de
massa de água liquida para vapor
a T e P constantes, temos que
adicionar energia (calor) ao
sistema, ou seja, calor latente.
No caso de liquido para vapor
utilizamos o calor latente de
vaporização.
da 1º lei da termodinâmica
 2
u 2
Lv 

dq ' 

u1
eq. (3)
du 

esd
 1
A seguinte notação é adotada para as
diferentes fases da água:
1-liquido, 2-vapor e 3-sólido.
Considerando que o processo de
mudança de fase é isotérmico e
isobárico, integramos a equação (3) de
uma fase a outra:
L v  (u
2
 u 1 )  e s (
eq. (4)
2
  1)
Combinando a mudança de fase a um
processo reversível; ou seja:
dS 
dq ´
T
TdS
 dq ´
Integrando
S 2

TdS


dq ´  L v
S1
Lv  T (S
2
 S1)
Lv  T (S
2
 S 1 )  (u
2
 u 1 )  e s (
2
 1)
Re-arranjando os termos por fases de estado
temos:
u 1  e s
1
 TS
1
 u
eq. (5)
2
 e s
2
 TS
2
u 1  e s
1
 TS
1
 u
2
 e s
2
 TS
2
• Esta igualdade mostra uma
combinação particular de
variáveis termodinâmicas que
permanecem constantes em uma
mudança de fase isotérmica e
isobárica.
• Esta combinação é conhecida
com a função de Gibbs que é
descrita como:
G  u 1  e s
1
 TS
1
• Logo a eq (5) se reduz a G1 = G2
Embora G seja constante durante a
transformação de fase, a função de
Gibbs varia (aumento da entropia),
logo T e P podem variar.
Dessa maneira, temos que analisar a
variação da energia livre de Gibbs
(dG) durante esta transição.
Processo
não-isotérmico e não-isobárico
dg  du  e s d    de
s
 TdS
 SdT
eq. (6)
Lembrando
G  u  e s   TS
• Levando em conta a
termodinâmica:
o
1
e
o
2
lei da
dq´ = du + esd
dq´= TdS
A eq. (6) se torna:
dg =  des – SdT
eq. (7)
A seguir supomos a vaporização de uma
unidade de massa de água liquida em
um processo reversível. Assim, temos
que:
G1=G2
• Mas como teremos uma variação da
energia livre de Gibbs durante a
transição, temos que G irá variar, logo:
G1 G1+dG1
G2  G2+dG2
Mas como
G1 = G2 e G1+dG1 = G2+dG2
Então  dG1= dG2, logo:
 1 de
s
 1
 S 1 dT   2 de


de
2
s

S 1
s
 S 2 dT
 S 2  dT
de
s

dT
(S
(
2
 S1)
2
  1)
Lembrando:
(S
2
 S1) 
Lv
T
de
dT
s

Lv
T (
2
  1)
eq. (8)
Equação de Clausius-Clapeyron
Analogamente podemos ter as
transições de vapor-sólido e liquido e
sólido
de

s
dT
Lv
T (
Vapor - Liquido
 1)
2
de
Vapor - Sólido
dT
de
dT
sf

L
T (
1
f

3
)
si

Ls
T (
2
 
3
)
Sólido- Liquido
Vapor - Liquido
de
Lv

s
T (
dT
  1)
2
 0

 
2
1
Vapor - Sólido
de
si

dT
Ls
T (
 0
  3)
2

2
 
3
Sólido- Liquido
de
dT
sf

L
T (
1
f
  3)
 0
1  
3
esfT)
es(T)
esi(T)
• Em condições atmosféricas, temos
que o volume específico do vapor
>> liquido (2 >> 1), e o vapor
age como se fosse um gás ideal.
• Analogamente também temos que
2 >> 3 (vapor>>sólido)
Simplificando a eq. Clausius-Clapeyron
(C.C.),
de
s

dT
Lv
T
eq. (9)
2
Da equação do estado do vapor temos: =RvT/es
de
dT
s

Lves
R vT
2
Assumindo que o Calor Latente de
vaporização é cte, podemos integrar a
equação (9):
es ( T )

de
s

Lv
Rv
T

dT
es 0  6 . 11
es
 es
ln 

 e so

Lv  1
1 
 




R v  To
T 

To
T
2
e s  e so
 Lv  1
1 
exp 



T 
 R v  To
eq. (10)
Similarmente para a fase sólida
e si  e so
onde
o
To=273
 Ls  1
1 
exp 



T 
 R v  To
K
25
ES
Ei
Pressao de Vapor (mb)
20
15
10
5
0
-30
-25
-20
-15
-10
-5
0
Temperatura (C)
5
10
15
20
10
ES
Ei
9
8
Pressao de Vapor (mb)
7
6
5
4
3
2
1
0
-30
-25
-20
-15
-10
Temperatura (C)
-5
0
5
0.50
ES-Ei
Pressao de Vapor (mb)
0.40
0.30
0.20
0.10
0.00
-30 -28 -26 -24 -22 -20 -18 -16 -14 -12 -10 -8 -6 -4 -2
Temperatura (C)
0
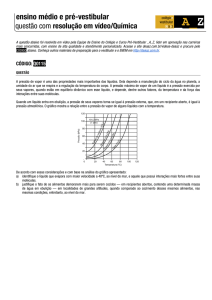
Diagrama que esquematiza as possíveis
situações entre e, es, e ei em uma
nuvem com fase mista:
(a) e > es e e > ei  processo onde tanto
as gotas liquidas como as particulas de
gelo crescem;
(b) e < es e e > ei  processo onde as
gotículas líquidas evaporam e as
partículas de gelo crescem – processo
de WBF;
(c) e < es e e < ei  processo onde tanto
as gotículas de água como as
particulas de gelo evaporam.
Korolev, JAS 2006.
Lista 1 – Entrega 26 de Agosto de 2016
1 - Fazer resumo do Artigo de Alexei Korolev: Limitations of the Wegener–
Bergeron–Findeisen Mechanism in the Evolution of Mixed-Phase Clouds, JAS, Vol.
64, pp 3372-3375, 2007.
http://www.storm-t.iag.usp.br/pub/AGM5818/Artigo_1_JAS4035.1_processo_bergeron.pdf
2 – Aplique a equação de Clausius-Clapeyron para o Metanol e calcule a pressão
de vapor de saturação para temperaturas de -100 a 100oC e compare com a água.
3 – Aplique a equação de Clausius-Clapeyron para o Amônia e calcule a pressão de
vapor de saturação para temperaturas de -100 a 100oC e compare com a água.
Seminário 1 – 26 de Agosto de 201
http://www.storm-t.iag.usp.br/pub/AGM5818/Artigo_1_JAS4035.1_processo_bergeron.pdf