Anlise de Fadiga em Estruturas de Heliponto

22º CONGRESSO NACIONAL DE TRANSPORTE AQUAVIÁRIO,
CONSTRUÇÃO NAVAL E OFFSHORE - SOBENA 2008
ANÁLISE DE FADIGA EM ESTRUTURAS DE HELIPONTO
Roberto Presta – KROMAV ENGENHARIA LTDA – [email protected]
Fernando Jorge Mendes de Sousa - COPPE/LACEO - [email protected]
Gilberto Bruno Ellwanger – COPPE/UFRJ – [email protected]
José Marcio do Amaral Vasconcelos – EP&COPPE/UFRJ – [email protected]
Severino Fonseca da Silva Neto – EP&COPPE/UFRJ – [email protected]
Introdução
O objetivo do presente trabalho é apresentar
de forma simplificada, um conjunto de
informações para análise de resistência de
componentes estruturais e a utilização destas
para o dimensionamento e estudo do
comportamento de fadiga em estruturas
offshore, mais precisamente das estruturas de
helipontos.
As estruturas de Heliponto são largamente
utilizadas em unidades fixas e flutuantes, tais
como FPSO, FSO e plataformas de
perfuração, podendo estas ser semisubmersíveis ou fixas, sendo de extrema
necessidade que o seu projeto receba uma
atenção especial em função do elevado grau
de segurança que é demandado na sua
operação.
A metodologia empregada para tal estudo
baseou-se em uma análise com o auxílio do
método numérico dos elementos finitos.
1
Metodologia de projeto
O desenvolvimento de um projeto tem início
quando existe uma exigência ou necessidade
do mercado para aquele tipo de trabalho.
Normalmente a definição dos requisitos de um
equipamento ou sistema de engenharia,
quando de grande porte, demanda uma série
de discussões entre fabricantes e clientes.
O projeto estrutural deve estar baseado em
requisitos de operação do sistema, ou em um
conjunto de condições a serem satisfeitas,
como por exemplo, eventuais sobrecargas
devido a falhas, falhas humanas na operação,
condições normais de uso ou ainda condições
de emergência.
Um dos grandes problemas da engenharia do
projeto é a incerteza que existe na
quantificação das variáveis necessárias para o
projeto, onde esta quantificação pode ser
estimada por uma análise aproximada,
baseada em experiência anterior, ou poderá
ser realizada por determinação experimental
através de ensaios das variáveis.
Em casos de equipamentos e sistemas de
engenharia de grande responsabilidade tornase necessário o ensaio de protótipos em
condições tão próximas quanto possível do
real para que se tenham informações
confiáveis sobre os carregamentos, ciclos de
trabalho, etc.
Alguns dos mais importantes itens para o
desenvolvimento de um projeto são:
• Determinação de esforços: Para estruturas
estáticas não existem grandes problemas da
determinação de cargas. No entanto, para
estruturas sujeitas as cargas ambientais
dinâmicas, a situação demanda um estudo
mais profundo.
A determinação destes
esforços dinâmicos pode ser realizada através
da análise teórica, onde será utilizado um
modelo matemático que representa este
comportamento, ou ainda, ser realizado
através de uma análise experimental, onde
poderemos determinar as cargas com a
estrutura em condições típicas de utilização.
• Análise de Tensões: Para a determinação
da metodologia de análise deve ser
primeiramente identificada a conveniência, a
disponibilidade e a responsabilidade da
1 / 15
estrutura. Esta análise pode ser realizada
através de vários métodos, como por exemplo,
o mais simples que se baseia na metodologia
da Mecânica dos sólidos.
Um método mais elaborado é o da Teoria da
Elasticidade, que procura determinar o campo
de tensões e deformações, tomando por base
apenas a geometria, carregamento e
condições de contorno.
• Análise de Falha: A resistência do material
que forma a estrutura é fundamental, pois é o
termo de comparação para se definir o nível
de segurança do componente. Esta resistência
deve ser comparável com o modo de falha que
o material poderá apresentar. Nesta etapa
procura-se determinar a tensão nominal que
pode solicitar o material, sem provocar falhas,
para o período de vida previsto para a
estrutura ou componente. Assim são usados
os métodos mais recentes para Análise de
Fadiga, bem como os conceitos da mecânica
da fratura, para análise do efeito nocivo de
fissura e eventuais defeitos internos do
material.
• Análise de Segurança: Nesta última etapa,
reunimos os resultados anteriores com as
informações referentes aos graus de
segurança necessários, bem como às
dispersões que ocorrem nos dados, para a
definição do coeficiente de segurança ou fator
de projeto adequado. Neste tópico entram os
conceitos de confiabilidade estrutural, onde o
aspecto aleatório das variáveis de projeto é
considerado. Esta aleatoriedade ocorre no
carregamento que atua sobre o produto e nas
propriedades do material. As tolerâncias
dimensionais são outra fonte de aleatoriedade
significativa quando tratamos de ajuste. Nesta
análise o objetivo é verificar se o nível de
resistência é adequado, comparativamente
com as flutuações de carga induzidas pelo uso
da estrutura ou do componente.
Assim poderemos avaliar se o projeto está de
acordo com os requisitos, sendo portanto
liberado para construção ou deve ser revisado,
retornando às etapas anteriores.
2
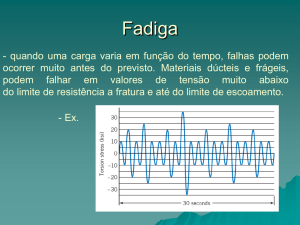
Introdução à fadiga
A grande maioria dos cursos de graduação na
área de engenharia não trata de maneira
direta o estudo de fadiga. Normalmente, na
Teoria da Resistência dos Materiais, são
realizadas
verificações
envolvendo
carregamentos de um único ciclo, também
chamados de carregamentos estáticos. Ao
contrário disto, a maioria das estruturas é
submetida
a
carregamentos
repetidos
compostos por muitos ciclos, como por
exemplo, pontes, peças de máquinas, aviões,
tubulações e estruturas offshore. Sob a ação
cíclica das cargas ambientais, particularmente
das ondas, no caso dos navios e estruturas
offshore, as juntas soldadas tornam-se sujeitas
à formação de trincas que eventualmente
poderão vir a se propagar.
Descreve-se como fadiga o processo de
alteração estrutural permanente, progressivo e
localizado, que ocorre num material sujeito a
condições que produzem tensões ou
extensões dinâmicas num ponto ou vários
pontos, e que podem culminar em trincas ou
numa fratura completa após um número
suficiente de variações de carga.
O dimensionamento ou análise de um
componente ou sistema estrutural envolve
uma seqüência de procedimentos, onde
normalmente inicia-se com a determinação
das solicitações devido ao carregamento
atuante e na análise de tensões nas seções
mais críticas. Paralelo a isto, o material possui
uma capacidade de suportar cargas que não
pode ser excedida, sem o inerente risco de
falha. Assim a tensão calculada é usualmente
comparada com uma tensão característica do
material, normalmente a tensão admissível
para cada tipo de aplicação.
A fadiga pode então ser classificada em dois
tipos:
• Baixo ciclo: alto nível de tensão, quando
temos um número de ciclos relativamente
4
3
pequeno, menos de 10 ou 10 ;
• Alto ciclo: baixo nível de tensão, quando
temos um número de ciclos relativamente
4
grande, mais de 10 ciclos, em alguns casos
6
9
podendo chegar na ordem de 10 a 10 ciclos.
No caso das estruturas offshore, os elementos
estruturais são dimensionados para responder
às solicitações no regime elástico, sendo
assim, sujeitos apenas à fadiga de alto ciclo.
Quando um elemento estrutural é submetido a
2 / 15
um carregamento cíclico, uma trinca por fadiga
pode desenvolver-se na região de máxima
tensão de tração. A pré-existência de uma
concentração de tensões, como um orifício,
chanfro, descontinuidade ou mesmo um
defeito, próximo à região de máxima tensão de
tração poderá ocasionar o início de uma trinca
por fadiga.
A propagação da trinca efetua-se pelo metal
de base, metal depositado ou na zona
termicamente afetada (ZTA), dependendo da
geometria da junta, estado metalúrgico do
material, tensões residuais e condições de
solicitação. Um dos fatores principais dos
problemas de juntas soldadas é que estas, em
geral, têm um perfil bruto e áspero. As
acentuadas alterações de sentido ocorrem
geralmente nas terminações das soldas de
topo e nas terminações e nas raízes das
soldas de filete. Estes pontos, por serem
descontinuidades, ocasionam nas suas
fronteiras tensões superiores a tensão nominal
ou a tensão média da seção, facilitando o
aparecimento das trincas e a sua conseqüente
propagação.
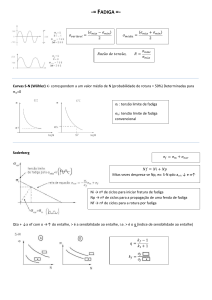
. Definição de Resistência à Fadiga e Vida à
Fadiga
A resistência à fadiga de uma estrutura
soldada é definida como a faixa de tensão (Δσ)
que varia com determinada amplitude,
causando falhas nos componentes após um
número especificado de ciclos (N). A faixa de
tensões pode ser definida como sendo a
diferença entre a tensão máxima e mínima do
ciclo. O número de ciclos em que a estrutura
possivelmente apresentará falha é conhecido
como a resistência ou vida à fadiga.
fadiga, ou, em termos práticos, se aumentar a
fase de iniciação da trinca. Consegue-se isso
aumentando a resistência mecânica do aço,
que conduz a um aumento da fase de
iniciação de uma trinca.
. Tipos de Carregamentos de Fadiga
Apresentamos abaixo algumas estruturas e os
carregamentos que podem eventualmente
causar fadiga:
• Pontes: Veículos comerciais, trens de carga;
• Guindastes: Içamento de cargas,
movimentação lateral e cargas inerciais;
• Estruturas Offshore: Ondas ( acelerações );
• Chaminés Delgadas: Rajadas de vento.
O objetivo do projetista é o de antecipar a
seqüência de cargas de operação durante
toda a vida da estrutura. A amplitude do valor
máximo de carga, que é vital para definição de
carga estática de projeto, é normalmente de
pouco
interesse
porquanto
representa
somente um carregamento em milhões de
ciclos.
A seqüência é importante porque afeta a
escala de tensões, particularmente se a
estrutura é carregada por mais de um sistema
independente da carga. Por conveniência, os
carregamentos são simplificados geralmente
em um histograma de carregamento, que
define uma série das faixas constantes de
níveis de carga, e o número de vezes que
cada faixa é experimentada, como abaixo.
. Fatores que afetam à vida à fadiga
A existência de chanfros, orifícios ou qualquer
outro elemento que aumenta a tensão na
vizinhança, causando concentrações de
tensões afetará o comportamento da iniciação
de fadiga em um material.
Para baixo número de ciclos de aplicação da
carga e tensões elevadas, a fase de iniciação
será praticamente nula, enquanto que, para
elevado número de ciclos e baixa tensão, a
fase de iniciação poderá ser elevada.
Pode-se aumentar a resistência à fadiga global
em uma estrutura soldada se diminuir a
probabilidade de iniciação de uma trinca de
Figura 1 – Espectro típico de carregamento de
projeto,[4]
Um ciclo de tensão de fadiga traduz a variação
da tensão aplicada com o tempo ou com o
número de ciclos da aplicação da carga.
Os dois tipos mais comuns de carregamento
são o de amplitude constante e o de amplitude
variável.
3 / 15
. Amplitude Constante
É representado pela variação constante de
tensão durante todo o carregamento (a
amplitude de tensão não varia com o tempo).
Na prática, isto se verifica em mecanismos
que funcionam a velocidade constante:
tirantes, rolamentos, engrenagens, polias, etc.
A figura abaixo ilustra este carregamento.
por:
onda,
vento,
corrente,
pressão
hidrostática variável, máquinas, forças de
restauração dos sistemas de amarração,
dentre outras. As forças de onda são
geralmente as fontes principais de falha por
fadiga em estruturas offshore.
Na prática, os carregamentos de fadiga
reais são simplificados em combinações
diferentes de carregamentos de amplitude
constante (com certa margem de segurança),
formando ciclos em blocos, onde se tem uma
sucessão bem definida de ciclos de tensão em
que se pode considerar vários blocos com
amplitude de tensão constante em cada bloco.
. Verificação da vida à Fadiga à amplitude
constante
Figura 2 – Histórico da variação de Tensão
com amplitude constante, [1]
Onde:
t – eixo do número de ciclos
σ - eixo das tensões
Δσ - dupla amplitude de tensão
A tensão média é definida por:
σm =
(σ máx + σ mín )
2
(1)
A amplitude de tensão corresponde à metade
da variação total do ciclo de tensão, ou seja:
σa =
Δσ
2
=
(σ máx − σ mín )
2
(2)
. Amplitude variável ( ao acaso )
Este tipo de ciclo não apresenta uma lei
definida entre as tensões e o tempo. Em geral,
é o tipo mais freqüente de ciclos de tensões
que provoca fadiga e, também, o mais difícil
de analisar.
Como exemplo de carregamento com
amplitude variável tem-se:
• Tráfego de caminhões em pontes;
• Carga de vento nos aviões;
• Carga de onda em Estruturas Offshore.
Carregamentos variáveis podem ser
impostos durante todas as fases da vida da
estrutura e podem, a princípio, ser causados
O dimensionamento à fadiga, segundo a
filosofia tradicional de projeto de máquinas não
baseada na mecânica da fratura, faz-se de
modo semelhante ao das solicitações estáticas
estabelecendo uma tensão admissível para
uma determinada vida ou duração. A tensão
admissível será a resistência à fadiga
calculada ou determinada para a peça ou
estrutura a dividir por um coeficiente de
segurança apropriado, coeficiente este que
deve tornar a ruptura por fadiga altamente
improvável. Esta filosofia de projeto é
tradicionalmente chamada de vida garantida.
É importante observar que no caso offshore
esta filosofia não é aplicada, pois utiliza-se o
conceito de vida útil, estipulando uma
determinada vida que a estrutura deve resistir
e aplicando um coeficiente de segurança nesta
vida útil e fazendo seu cálculo pela
metodologia do cálculo do dano cumulativo
pela Regra de Miner.
Como a curva S-N é feita para condições
ótimas, calcula-se a resistência à fadiga, para
um
determinado
número
de
ciclos,
considerando vários fatores de redução que
levam em consideração os principais
parâmetros do processo de fadiga.
. Verificação da vida à Fadiga à amplitude
variável
Nas condições reais de campo, elementos ou
estruturas são usualmente submetidos a um
número de diferentes níveis de tensão,
tensões médias, etc.
4 / 15
Figura 3 – Esquema com valores de R e faixas
de tensão com cargas de amplitude variável,
[1]
Sabe-se que a ocorrência de danos por fadiga
é considerada um estado limite, por isso, para
garantir um grau de “confiabilidade” elevado
em serviço é necessário ter em conta a
possibilidade de iniciação e posterior
propagação de trincas de fadiga quando as
cargas aplicadas variam de intensidade com o
tempo (como mostrado na Figura 4).
A dedução dessas curvas de projeto é feita
analisando estatisticamente os resultados
experimentais (duração ou vida) para vários
níveis de tensão de amplitude constante.
A curva de projeto é obtida unindo os pontos
correspondentes
a
uma
determinada
probabilidade de colapso. Os modelos
matemáticos ou funções de densidade de
probabilidade que tem sido propostos para
descrever a dispersão da duração à fadiga são
diversos (distribuição normal, log-normal,
Weibull, etc.).
Com base nessa metodologia, é possível
determinar a tensão admissível para uma
determinada duração prevista, assumindo uma
determinada probabilidade de colapso,
podendo esta tensão ser ou não afetada por
um coeficiente de segurança.
A consideração do caráter aleatório da
amplitude de tensão aplicada torna mais difícil
a
análise
com
base
em
critérios
probabilísticos, pois, além do caráter aleatório
da resistência à fadiga, é necessário ter
também em conta o caráter aleatório da
grandeza da tensão aplicada. A elevação da
superfície do mar geralmente não possui
características regulares, e sim uma forma
irregular.
Os períodos de onda (Ti) para esse estado de
mar são definidos como sendo o tempo entre
sucessivos cruzamentos da superfície do mar
ao nível médio, e suas alturas (Hi) definidas
como a diferença entre os valores máximo e
mínimo dentro de um período onda.
Num pequeno intervalo de tempo (3 horas), as
propriedades estatísticas do estado de mar
podem ser consideradas constantes e o mar
pode ser denominado estacionário. São feitas
medições que duram 20 minutos para
representar um estado de mar.
Os seguintes termos são usados para
descrever um estado de mar estacionário:
• Período de cruzamento zero (Tz) é a média
dos valores dos períodos da onda (Ti) ou
então (Tp), período de pico do espectro;
• Altura de onda significativa (Hs) é a média do
terço mais alto das alturas de onda.
O cálculo dos carregamentos hidrodinâmicos
para uma análise de fadiga pode ser feito
através do método determinístico ou do
método probabilístico.
No método determinístico do carregamento
hidrodinâmico, a estrutura é carregada com
uma onda regular, representada por sua altura
H, pelo período T, usando-se uma teoria de
onda adequada. Uma corrente de projeto pode
ser incluída. A direção da corrente é
geralmente considerada igual à direção da
incidência da onda e a velocidade de onda e
corrente será adicionada vetorialmente.
A análise de fadiga espectral envolve os
seguintes passos:
• Seleção das principais direções de incidência
de onda (o número total de ondas é distribuído
entre essas direções principais). Direções
principais de propagação de onda devem ser
incluídas, como também as direções que
causam tensões elevadas nos principais
elementos da estrutura;
• Para cada direção, seleciona-se um número
de estados de mar que descrevem
adequadamente a distribuição de longo prazo
das ondas. Associa-se a um percentual de
ocorrência de cada estado de mar;
• Estabelecimento de uma função de
transferência para cada variável de interesse;
• Cálculo do espectro de resposta para cada
estado de mar, combinando o espectro de
onda e as funções de transferência;
5 / 15
• Cálculo das faixas de tensões para cada
estado de mar;
• Combinação dos resultados para todos os
estados de mar para encontrar a distribuição
de longo prazo dos valores de resposta;
• Cálculo da vida à fadiga, geralmente
utilizando-se a regra de Miner, descrita no
paragrafo seguinte.
Uma abordagem freqüente consiste em se
usar resultados de ensaios de amplitude
constante em conjunto com a lei de danos
cumulativos de Miner para prever o
comportamento dos elementos submetidos a
condições variáveis de carregamento.
A hipótese básica da regra de Miner é a de
que o dano sobre a estrutura por ciclo de
carregamento é constante numa dada faixa de
tensões, sendo igual a:
(3)
Onde N = f(σ) extraído da curva S-N.
Neste caso, o ciclo de amplitude de tensão
variável é assimilado a um conjunto de n
blocos, em que cada bloco tem uma amplitude
de tensão constante σ e dura n ciclos.
i
i
A Lei de Miner estabelece que os danos (isto
é, perda de vida de fadiga) se acumulam de
modo linear e é dada por:
(4)
Onde:
• k = n0 de diferentes níveis de tensão em uma
específica seqüência de carregamento;
• i = i-ésimo nível de tensão naquela
seqüência de carregamento
• n = número de ciclos de carregamento a um
i
nível de tensão σ ;
i
• N = vida de fadiga a um nível de tensão de σ
i
i
(número total de ciclos de carregamento a um
nível de tensão σ que a estrutura resiste).
i
Além disso, é praticamente impossível preverse para uma estrutura real qual será a
seqüência de cargas que ela estará submetida
durante a sua vida útil.
A lei de Miner não toma em consideração
aspectos que experimentalmente já se
verificou terem bastante influência na duração
à fadiga:
• Considerar que as tensões inferiores à
tensão limite de fadiga não provocam
alteração do material;
• Considerar a resistência à fadiga
independente da história de carga.
A vida à fadiga é dada por:
(5)
Onde:
L = tempo relativo ao número total de ciclos
0
de tensão n = Σ n , que, normalmente, se
0
i
utiliza 1 ano;
D = somatório total do dano.
Apesar das imprecisões, a lei de Miner
continua a ser largamente utilizada na prática
devido à sua simplicidade matemática e ao
fato de fornecer resultados com certa margem
de segurança.
. Modo espectral de cálculo do
carregamento à fadiga
O sinal aleatório é diferente de um
determinístico, possuindo freqüência variável e
podendo apresentar-se muito mais complexo.
Neste item, tem-se o objetivo de apresentar
uma metodologia para lidar com esse tipo de
carregamento utilizando o método espectral.
Quando se lida com um tipo de carregamento
que não é constante e não pode ser
determinado precisamente por uma função, ou
seja, não se pode prever com 100% de
certeza o que irá ocorrer num determinado
instante, diz-se que esse carregamento é
estocástico.
Um processo é dito estacionário se as
propriedades estatísticas não variam com o
tempo. Muitos processos podem ser
considerados estacionários se o intervalo de
tempo em que são analisados for
suficientemente curto. A elevação da
superfície do mar, por exemplo, é
normalmente considerada estacionária dentro
de intervalos de três a seis horas.
6 / 15
. Curvas S-N
A vida à fadiga de juntas soldadas pode ser
representada através de curvas que
relacionam a amplitude das solicitações (S) e
o número de ciclos de carregamento (N),
chamadas de curvas S-N. No entanto, o
cálculo convencional do dano por fadiga numa
junta soldada com a adoção da regra de Miner
associada a curvas S-N não permite avaliar os
estados intermediários da propagação de uma
trinca, pois essas curvas não permitem que
sejam consideradas separadamente as fases
de iniciação e propagação das trincas.
As curvas S-N são levantadas a partir de
testes simulados de laboratório. Um aparelho
de teste deve ser projetado para reproduzir de
maneira tão próxima quanto possível as
condições de tensão em serviço.
A obtenção de uma curva S-N é feita
estatisticamente. As curvas S-N de projeto são
adotadas
baseadas
em
técnicas
de
probabilidade de falha. Assim, adota-se a
curva média menos dois desvios padrões para
a sua obtenção (correspondente a uma
probabilidade de falha de 2,5 %).
Deve-se salientar que a curva S-N engloba as
fases de iniciação e propagação da trinca por
fadiga sem que haja uma distinção entre as
mesmas.
. Efeitos da tensão média
Em detalhes não-soldados a resistência é
reduzida enquanto a tensão média torna-se
maior. Em detalhes soldados a resistência não
é normalmente reduzida nestas circunstâncias.
Este comportamento ocorre porque as tensões
de encolhimento de solda (ou tensões
residuais), as quais ficam presas nas juntas
soldadas durante a fabricação, com freqüência
alcançam a tensão de escoamento. As trincas
não distinguem a tensão aplicada da tensão
residual.
Assim, para a finalidade de projeto, as curvas
S-N sempre assumem a pior condição, isto é,
que a tensão máxima do ciclo está no ponto
de escoamento da tensão.
. Efeitos da Resistência Mecânica
A taxa do crescimento das trincas não é
afetada significativamente por variações
profundas de tensão ou tensões últimas dentro
da faixa dos aços de baixa liga usados em
estruturas em geral. Estas propriedades
somente afetam o período da iniciação, o qual,
vem sendo negligenciados nas soldas, e que
resultam em pouca influência na vida da
fadiga. Este comportamento contrasta com a
fadiga de detalhes não-soldados onde o
aumento da resistência mecânica resulta
geralmente no aumento da resistência à
fadiga.
. Tipos de Detalhes
Existe usualmente um número de tipos de
detalhes dentro de cada classe. A principal
característica que afeta o tipo de detalhe, e,
portanto sua classificação, são:
• Forma do membro: como por exemplo,
chapas, perfis laminados, barras reforçadoras,
etc;
• Localização antecipada da iniciação da
trinca: a localização deve ser definida em
relação à direção da tensão flutuante. Dada
uma determinada junta soldada que contenha
mais de um ponto potencialmente sujeito a
trinca, em qual dos casos a junta poderá vir a
falhar em dois ou mais tipos de detalhes;
• Dimensões principais: formato da solda,
tamanho dos componentes, proximidade das
arestas, mudanças abruptas das seções
transversais;
• Requisitos de Fabricação: como por
exemplo, tipos do processo de soldagem,
adoçamento por esmerilhamento de qualquer
parte da junta;
• Requisitos de Inspeção: procedimentos
especiais de inspeção devem ser requeridos
para as classes mais altas de detalhes de
forma a assegurar que defeitos de solda não
estejam presentes.
3
Aplicação em um projeto determinado
As informações apresentadas nos tópicos
anteriores tiveram por objetivo introduzir de
forma simplificada e sucinta a teoria aplicada à
fadiga, a obtenção dos dados e características
que podem apresentar influência a vida à
fadiga. A partir deste ponto, destinaremos
espaço a apresentação de um procedimento
de cálculo para a verificação estrutural de um
Heliponto, estrutura geralmente construída de
treliçada, onde são utilizados perfis tubulares
em conjunto com vigas laminadas ou
fabricadas tipo “ I “ ou “ H “.
7 / 15
¾
Roteiro das etapas do projeto
• Determinação da estrutura: preparação do
projeto da estrutura do heliponto, a partir da
confecção dos documentos necessários que
serão utilizados posteriormente na construção,
procurando verificar possíveis problemas
estruturais e pontos de apoio a serem
considerados;
• Verificação preliminar da estrutura:
realização de um cálculo manual utilizando as
sobrecargas possíveis para determinação das
tensões atuantes e comparação destes
valores com as tensões admissíveis;
• Determinação do método de cálculo:
dentro das normas aplicáveis, sendo estas
entidades certificadoras (classificadoras) ou
normas
de
instituições
nacionais
e
internacionais,
torna-se
necessário
a
determinação do método de cálculo a ser
adotado para o desenvolvimento do projeto,
podendo ser:
- WSD – Working Stress Design, também
conhecido como método das tensões
admissíveis;
- LRFD - Load and Resistance Factor Design,
método onde as incertezas das cargas são
representadas com fatores de majoração do
carregamento e as incertezas devido a
resistência são representadas com fatores de
majoração chamados de “fatores de material”.
• Análise das tensões: Após a incorporação
ao modelo de cálculo de todos os
carregamentos atuantes, cargas efetivas e
ambientais,
deverão
ser
realizadas
verificações das tensões atuantes na
estrutura.
Estas tensões atuantes deverão estar abaixo
dos limites das tensões admissíveis (método
WSD) ou abaixo do limite da tensão de
escoamento (método LFRD );
• Análise de vida à fadiga: Está etapa deve
obedecer a seguinte seqüência de análise:
- Através de estudos e dados observados para
a região de alocação da estrutura, selecionar
os estados de mar significativos para esta
análise;
- Escolha adequada de uma dada curva S-N
conforme o ponto da estrutura a ser estudada,
onde são fatores importantes o tipo de ligação
estrutural local e as condições ambientais a
que a estrutura está submetida (ambiente ar
ou ambiente água);
.Nesta fase, para cada estado de mar, o qual
se caracteriza pela junção das ocorrências de
onda, vento e corrente, deverão ser avaliadas
as tensões neste ponto da estrutura;
.Utilizando o método da fadiga determinística,
avaliar o dano correspondente a estas
variações de tensão para cada um destes
estados de mar.
- Somar os danos causados pelas variações
de tensão, o qual deve considerar o percentual
de ocorrência de cada estado de mar, e
calcular finalmente a vida à fadiga.
¾
Apresentação do Cálculo
Descreveremos um sumário da modelação,
carregamentos e os parâmetros utilizados para
a análise, onde uma análise quase-estática foi
elaborada de forma a obter as tensões
nominais.
Um modelo tri-dimensional foi elaborado
através de um programa de elementos finitos
(SESAM-DnV: Patran-Pre para a modelação e
o Framework para a análise da estrutura)
utilizando todos os elementos como elementos
de barra, exceto a parte do piso do heliponto,
que foi modelado em elemento de placa.
O modelo foi confeccionado utilizando os
dimensionais e afastamentos dos elementos
em “mm” e as cargas em “N”. As tensões
serão apresentadas em “MPa”.
De acordo com as normas foram considerados
quatro diferentes situações de análise, a saber:
- Análise Estática – peso próprio da estrutura +
carga distribuída sobre o piso e sobre as
estações de combate à incêndio ;
- Análise Quase-Estática (Condição de pouso)
– peso próprio da estrutura + acelerações +
vento atuante + carga de pouso do
helicóptero;
- Análise Quase-Estática (Condição pousado)
– peso próprio da estrutura + acelerações +
vento atuante + carga do helicóptero;
- Análise Quase-Estática (Condição de colisão
de emergência) – peso próprio da estrutura +
acelerações + vento atuante + carga de
impacto do helicóptero em queda.
Nas últimas três situações, o posicionamento
da carga do helicóptero foi realizado em 30
8 / 15
posições distintas sobre o piso, simulando
várias das possibilidades de pouso que
poderão ocorrer.
A distribuição das cargas de vento seguiu a
seguinte formulação [11]:
(6)
• P = pressão de vento ( N/m2);
• Vk = velocidade do vento;
• f = 0,611;
• Ch = coeficiente de altura;
• Cs = coeficiente de forma;
Figura 5 – Modelo Global do Heliponto
Os valores apresentados na tabela abaixo são
as máximas acelerações encontradas, através
de uma envoltória, para as diversas condições
ambientais (onda, vento e corrente) que
deverão ocorrer no local de instalação da
unidade. Na combinação de carregamentos
foram utilizadas as acelerações do calado de
operação.
Para o método de cálculo adotado ( LFRD ),
foram adotados os seguintes valores, a saber:
- Carga permanente (massa da estrutura) –
fator de multiplicação igual a 1,3;
- Carga variável (carga do helicóptero
pousando) – fator de multiplicação igual a 1,3;
- Carga ambiental (vento atuando) – fator de
multiplicação igual a 0,7.
¾
Verificação à fadiga
Várias considerações devem ser adotadas
para esta verificação, contudo, como o objetivo
deste trabalho é o de apresentar a
metodologia
de
cálculo,
diversas
simplificações foram assumidas explicitadas a
seguir:
- Considerado a ocorrência de apenas um
estado de mar;
- Simplificação da análise das tensões.
Para esta análise foram considerados os
seguintes carregamentos de vento em
conjunto com as acelerações, a saber:
Figura 6 – Tabela de Acelerações e Inclinação
máxima da Unidade.
Para a condição de operação irrestrita,
conforme as normas, a carga de vento
estabelecida é de 36,0m/s [10].
Os valores de referência para Bacia de
Campos, de acordo com estudos da
Petrobrás, para 10 metros acima da linha
d’agua e com duração de 10 minutos são:
Figura 7 – Dados medidos na Bacia de
Campos no período de 10/1986 até 05/2003
- Condição 1 - vento no sentido transversal,
vento no piso do heliponto devido a “roll” e
acelerações no sentido transversal da
embarcação;
- Condição 2 - vento no sentido longitudinal
(positivo), vento no piso do heliponto devido a
“pitch” e acelerações no sentido longitudinal da
embarcação;
- Condição 3 - vento no sentido longitudinal
(negativo), vento no piso do heliponto “pitch” e
acelerações no sentido longitudinal da
embarcação;
Como a estrutura se mostra simétrica no
sentido transversal, somente uma condição de
carregamentos combinados foi considerada
neste sentido. Após a realização dos
carregamentos, foi gerada uma envoltória de
9 / 15
resultados de tensões, onde somente os
pontos máximos serão estudados.
Para a execução do estudo à fadiga foram
escolhidos dois pontos, os quais se mostram
mais comuns dentro da estrutura:
- Junta cruciforme – união de vigas com soldas
de topo nos flanges;
- Junta com chapa “gusset”.
¾
Verificação para uma Junta Cruciforme
Utilizaremos o processo de análise de fadiga
simplificada, de acordo com a norma do DnV
[3], e como parâmetro inicial o projeto de vida
útil da estrutura deverá ser de 25 anos. Abaixo
apresentamos um “plot” da estrutura, onde
poderemos observar o elemento 53, que será
alvo de nosso estudo.
Figura 10 – Representação dos pontos de
tensão fornecidos pelo programa.
O fator de projeto da vida à fadiga (DFF) pode
ser obtido através da tabela A1 [9] como
sendo:
DFF = 2,0 (estrutura externa não acessível à
inspeção e reparo em condições satisfatórias)
Parâmetro de Weibull [10]
Onde:
( L ) é o comprimento da unidade = 322,0m
h0 = 0,855
Será adotado o valor de 0,9.
Figura 9 – Plot da estrutura com o elemento 53
Os elementos 53, 47 e 48, possuem as
seguintes dimensões:
• Cálculo do SCF
Para o cálculo do SCF de uma junta
cruciforme utilizaremos a formulação do Dnv
[7]:
Como output do programa, apresentamos a
seguir o resultado da tensão nominal para o
elemento 53, que é dado pela soma:
SigNor = tensão axial (SigXX) + tensão flexão no plano
YX (SigBYX) + tensão flexão no plano ZX (SigBZX)
O programa fornece as tensões em vários
pontos do elemento de viga. Neste caso, como
o objeto de estudo é a ligação entre flanges, o
ponto nº 11 será verificado por apresentar o
maior valor de tensão.
Figura 11 – Detalhe esquemático de junta
cruciforme / metodologia de verificação do
SCF ( 7 )
• δ = excentricidade total ( mm
m );
• δ0 = 0,3 t (excentricidade inerente a curva);
• t = espessura da chapa considerada;
• l = comprimento da chapa considerada.
10 / 15
Adotaremos a Curva W1, pois é a que melhor
atende ao estudo. Ela é utilizada nas ligações
entre flanges de perfis (I ou H). [7]
Figura 13 – Tabela de resultado da vida à
fadiga
¾
Figura 12 – Modelo de junta adotado
• Cálculo do Dano (D)
Para o cálculo do dano à fadiga utilizaremos a
formulação do Dnv [7]:
Verificação para uma Junta com chapa
“gusset”
Utilizaremos o processo de análise de fadiga
simplificada semelhante ao utilizado na
verificação da viga cruciforme.
Abaixo apresentamos um plot da estrutura,
onde poderemos observar o elemento 1290,
que será alvo de nosso estudo.
(7)
Onde:
• n0 = expectativa do nº de ciclos de trabalho;
• h = parâmetro de Weibull adotado;
• q = parâmetro de Weibull definido pelo nível
de tensão (Δσ0);
• Γ(1+m/h) = função gama;
n(ν 0 .Τd ) =
=
n 0 dias × n 0 horas x 3600 s
período
x 25anos =
365 x 24 x3600 s
x 25anos = 1,314 x10 8 ciclos
6s
Figura 14 – Plot da estrutura - ligação do
elemento1290
O elemento 1290 é um perfil tubular conectado
na sua parte superior a um perfil (I) através de
uma chapa “gusset”.
O período adotado de 6,0 segundos refere-se
ao período mínimo de onda.
n0 = 1,314 x108 x 4 = 5,256 x108 ciclos
Δσ 0 = 5,716 x107 x 2 / 106 = 114,32 MPa
D ≤ η ⇒ D ≤ 1 / DFF ⇒ 0,2109 ≤ 0,5
Figura 15 – Representação da estrutura
11 / 15
Como output do programa, apresentamos a
seguir o resultado da tensão normal para o
elemento 1290, que é dada através da
seguinte fórmula [13]:
(8)
O programa fornece ainda as tensões em
vários
pontos
do
elemento
tubular.
Utilizaremos neste caso, o ponto nº 7 por
apresentar o maior valor de tensão.
Figura 16 – Ilustração do modelo adotado para
determinação do SCF
Apresentamos a seguir, a descrição dos casos
de carregamentos utilizados para esta
verificação e os seus respectivos resultados
(“plots”):
- Caso 1 – Todas as extremidades engastadas
exceto o pilar central onde foi aplicada carga
de tração axial unitária;
- Caso 2 – Todas as extremidades engastadas
exceto o pilar lateral onde foi aplicada carga
de tração axial unitária;
Figura 15 – Representação dos pontos de
tensão fornecidos pelo programa
O fator de projeto da vida à fadiga (DFF) e o
parâmetro de Weibull [10] foram adotados de
forma semelhante ao cálculo da junta
cruciforme.
• Cálculo do SCF
Para a obtenção do valor do SCF deste tipo de
junta, houve a necessidade da elaboração de
um modelo isolado da região, onde foram
atribuídas diversas condições de contorno ao
modelo e utilizada uma carga de valor unitário
em vários dos elementos de forma a
detectarmos as variações dos valores de
tensão ao redor do ponto de concentração,
que neste caso, será a ligação do perfil tubular
com a chapa “gusset”.
Os valores das tensões de von Mises
apresentadas nas figuras estão em MPa.
- Caso 3 – Todas as extremidades engastadas
exceto o pilar central com carga unitária no
sentido transversal do modelo global gerando
momento;
- Caso 4 – Todas as extremidades engastadas
exceto o pilar central com carga unitária no
sentido longitudinal do modelo global gerando
momento;
- Caso 5 – Todas as extremidades engastadas
exceto o pilar lateral com carga unitária no
sentido transversal do modelo global gerando
momento;
- Caso 6 – Todas as extremidades engastadas
exceto o pilar lateral com carga unitária no
sentido longitudinal do modelo global gerando
momento.
12 / 15
Figura 17 – Caso 1 - SCF = 1,79
Figura 19 – Caso 3 - SCF = 1,64
Figura 18 – Caso 2 - SCF = 1,67
Figura 20 – Caso 4 - SCF = 1,82
13 / 15
Adotaremos a Curva F, pois é a que melhor
atende a ligação de perfil tubular e chapa
gusset. Ela é recomendada nas ligações de
chapas “gusset” montadas com soldas de
filete. [7]
Figura 22 – Modelo de junta adotado
• Cálculo do Dano (D)
Para o cálculo do dano à fadiga utilizaremos a
formulação do Dnv [7]. Ver cálculo do dano na
verificação da viga cruciforme.
Figura 21 – Caso 5 - SCF = 4,08
Figura 23 – Tabela de resultado da vida à
fadiga
4
Figura 21 – Caso 6 - SCF = 1,52
Considerações Finais
Em virtude da crescente preocupação de
diversas entidades e empresas da área
petróleo, sejam estas “onshore” ou “offshore”,
com a segurança das pessoas e com os danos
e prejuízos envolvidas nestas operações,
torna-se primordial estudos mais aprofundados
nas áreas da engenharia de forma a minimizar
estes efeitos.
A análise da fadiga em
estruturas offshore é um destes casos. Na
14 / 15
graduação dos profissionais de engenharia o
tema fadiga é tratado de forma rápida e
simplificada. No entanto, na fase profissional
torna-se de extrema utilidade o conhecimento
e domínio deste assunto, em virtude da sua
atual difusão e utilização na determinação de
estruturas.
Desta forma, procuramos
desenvolver e proporcionar ao longo deste
trabalho um texto sucinto com informações
pontuais sobre a verificação da vida à fadiga
em estruturas offshore, mais precisamente em
estruturas de heliponto.
Através dos estudos apresentados neste
trabalho, onde realizamos a determinação da
vida à fadiga através do método simplificado,
pudemos ter contato com a teoria do
desenvolvimento da fadiga e a metodologia a
ser aplicada na determinação da vida à fadiga,
além das formulações, normas adotadas e a
necessidade da escolha adequada das curvas
S-N.
É importante destacar que este estudo pode
ser mais aprofundado, na medida em que se
tenha um tempo maior de dedicação ao
assunto, pois existem diversas outras técnicas
de análise não mencionadas neste trabalho, e
que traduzem resultados com maior grau de
precisão.
[4] ESDEP, European Steel Design Education
Programme – Chapter 12 – Basic Introduction
to Fatigue;
[5] RIVA, IKARO DOS REIS – Análise de
Fadiga de Estruturas Metálicas com Ênfase
em Offshore, dezembro de 2004;
[6] MENDONÇA, SALETE MARTINHO de –
COPPE/UFRJ, M.Sc., Engenharia Civil, Tese
de Mestrado – Análise Da Estrutura De
Suportação De Um Riser Rígido Em Catenária
Em Uma Plataforma Semi-Submersível; [Rio
de Janeiro] Junho de 2001;
[7] DNV – DET NORSKE VERITAS; Fatigue
Design of Offshore Steel Structures;
Recommended Practice RP-C203; August
2005;
[8] DNV – DET NORSKE VERITAS; Helicopter
Decks; Offshore Standard OS-E401; March
2001;
[9] DNV – DET NORSKE VERITAS; Design of
Offshore Steel Structures, General (LFRD
Method); Offshore Standard OS-C101; April
2004;
[10] DNV – DET NORSKE VERITAS; Fatigue
Assessment of Ship Structures, Classification
Notes Nº 30.7; February 2003
5
Referências Bibliográficas
[1] WILLEMS, EASLEY, ROLFE, “Resistência
dos Materiais”, Editora Mc. Graw-Hill, capítulo
14, 1983;
[11] ABS – AMERICAN BUREAU OF
SHIPPING; Rules for Building and Classing Móbile Offshore Drilling Unit; 2001;
[2] MOURA BRANCO, CARLOS AUGUSTO
GOMES DE, “Mecânica dos Materiais”, 3ª
edição, Serviço de Educação Fundação
Calouste Gulbenkian/Lisboa, capítulos 10 e
14, novembro de 1998;
[12] ABS – AMERICAN BUREAU OF
SHIPPING; Shipbuilding and Repair Standard
for Hull Structures During Construction;
Julyn1998;
[3] MOURA BRANCO, CARLOS AUGUSTO
GOMES DE; FERNANDES, ANTÓNIO
AUGUSTO; CASTRO, PAULO MANUEL
SALGADO TAVARES DE, “Fadiga de
Estruturas Soldadas”, edição de Fundação
Calouste Gulbenkian, agosto de 1986;
[13] API – AMERICAN PETROLEUM
INSTITUTE; Recommended Practice for
Planning, Designing and Construction Fixed
Offshore Platforms – Working Stress Design;
API RP 2A-WSD; Twenty-First Edition,
December 2000.
15 / 15