Associacao de Resistores

Laboratório de Física
Experimento 01: Associação de Resistores
Disciplina: Laboratório de Física Experimental II
Professor: ______________________________________ Turma: _____ Data: ___/___/20___
Alunos (nomes completos e em ordem alfabética):
1: _____________________________________________________________________________
2: _____________________________________________________________________________
3: _____________________________________________________________________________
4: _____________________________________________________________________________
5: _____________________________________________________________________________
Laboratório de Física – UVV
2/15
01 – Associação de Resistores
1.1. Objetivos
➢
Operar um multímetro como ohmímetro, selecionar escalas mais favoráveis para uma
medida e manusear protoboard para a montagem de circuitos elétricos;
➢
Associar resistores em série, paralelo, associações mistas e comparar a resistência
equivalente teórica com os valores encontrados experimentalmente.
1.2. Equipamentos
Lista de equipamentos necessários para a realização do experimento:
✔
1 Multímetro;
✔
1 protoboard;
✔
6 Resistores de mesma ordem de grandeza (evite repetição nos valores nominais dos
resistores).
2. Apresentação
Neste experimento será empregado um conjunto de resistores para o estudo de associação em
circuitos em série, paralelo e mistos, com a intenção de verificar a física das associações e
desenvolver as habilidades no uso do multímetro com na medida de resistências e de seleção de
escalas convenientes.
2.1.
Associação de Resistores
As regras de associação de resistores são meras aplicações das Leis de Kirchhoff que estabelecem:
1. A soma das variações de tensão em uma malha fechada é sempre igual a zero;
2. A soma das correntes que entram em um nó, menos a soma das correntes que saem de um
nó é sempre nula.
2.1.1.
Associação em Série
Suponha um circuito com três resistores em série, como ilustra a Figura 1, alimentado por uma fonte
de potencial , que fornece uma corrente ao circuito. Neste caso o potencial elétrico da fonte será
dividido em três quedas de potencial, sobre os três resistores, como ilustra a figura. Este circuito
muitas vezes é chamado de Divisor de Tensão.
Laboratório de Física – UVV
3/15
Figura 1: Circuito para associação em série
Estes potenciais são facilmente determinados pela Lei de Ohm, e são dados pelas equações:
Portanto, a soma destes potenciais tem que ser igual ao potencial da fonte, ou seja,
Ou na forma da Lei de Kirchhoff para as Malhas, “a soma dos potenciais em uma malha fechada é
igual a zero”,
De uma forma ou de outra, podemos escrever esta expressão na forma,
onde
é a soma das três resistências em série. Uma expressão mais geral para
seria
(1)
Portanto, para a associação de resistores em série, a resistência equivalente é dado pela soma das
resistências em série. Um outro ponto relevante que pode ajudar a identificação de resistores em
série é o fato que “em todos os resistores em série flui a mesma corrente, enquanto o potencial de
divide”.
2.1.2. Associação em Paralelo
A Figura 2 apresenta o circuito da associação de três resistores em paralelo. Observe que os pontos
e
no circuito da Figura 2-(a) possuem o mesmo potencial elétrico, uma vez que não existem
resistores entre eles1. O mesmo ocorre com os pontos e , na base do circuito da Figura 2-(a). Do
pondo de vista elétrico estes pontos são considerados o mesmo ponto e, portanto, possuem o
mesmo potencial elétrico. Ou seja, o potencial elétrico no polo superior da fonte (
) é o mesmo
nos terminais superiores dos resistores
,
e . O mesmo ocorre com o polo inferior da fonte (
), que é o mesmo nos terminais inferiores dos resistores
,
e
. Isto significa que os três
resistores estão sobre o mesmo potencial elétrico, no caso o potencial da fonte.
1
Nestes casos consideramos os fios ideais e portanto não possuem resistência.
Laboratório de Física – UVV
4/15
Figura 2: Duas representações da associação de três resistores em paralelo.
No entanto, observe que a corrente elétrica é dividida pelos resistores em três porções:
A corrente total pode ser determinada pela soma das três correntes,
Ou pela Lei de Kirchhoff para os Nós, “a soma das correntes que entram em um nó, menos a soma
das correntes que saem deste nó, é sempre nula”, que aplicada ao nó superior dará a mesma
expressão acima. Substituindo as expressões para as correntes acima, temos:
onde
é dado por,
ou de uma forma mais compacta
(2)
Laboratório de Física – UVV
5/15
Portanto, para a associação de resistores em paralelo, a resistência equivalente é dada pelo inverso
da soma dos inversos das resistências em paralelo.
2.2. Resistores Comerciais
Para as atividades, serão empregados resistores comerciais de
de potência máxima2 e com
de tolerância, embora alguns resistores de
possam ser encontrados no laboratório. Estes
resistores são constituídos por um cilindro de cerâmica, pintados por uma tinta de compostos de
carbono e mais algum metal, usualmente ferro. O comprimento e a espessura destas faixas resultam
na resistência do dispositivo.
Resistores comerciais são constituídos em valores padrões de resistências como
,
,
,
,
,
,
,
,
e múltiplos de
destes valores, para resistores de dois
algarismos.
Estes valores comerciais são chamados de “Valor Nominal” do resistor e geralmente são
representados através de um código de cores gravados nos resistores em 4 faixas. A Tabela 1
mostra o código de cores, para cada faixa, em um resistor de 4 faixas.
COR
1ª Faixa
Preto
-
Marrom
Vermelho
1
2
2ª Faixa
3ª Faixa
4ª Faixa
0
10
0
-
1
10
1
-
2
10
2
-
3
-
Laranja
3
3
10
Amarelo
4
4
104
-
Verde
5
5
105
-
Azul
6
6
10
Violeta
7
7
-
-
Cinza
8
8
-
-
Branco
9
9
-
Dourado
-
-
Prateado
-
-
6
-
10
-1
5%
10
-2
10%
Tabela 1: Tabela com código de cores para resistores de carbono.
Nestes resistores, as duas primeiras faixas representam dois dígitos, a terceira uma potência de
a quarta a tolerância do resistor.
e
A Figura 3 apresenta um resistor comercial de
de tolerância. Se olhar na Tabela 1, verá que a
primeira faixa, amarela, corresponde ao dígito e a segunda, violeta, ao dígito . Estas duas faixas
representam os dígitos
do valor da resistência. A terceira faixa, cor vermelha, corresponde a
potência de
. Portanto o valor nominal deste resistor é de
. A última faixa é sempre
dourada ou prateada, que correspondem a tolerância de
e
, conforme a Tabela 1.
2
Conhecidos como resistores de 1/4 de potência. A potência do resistor é dada pelo tamanho do dispositivo e,
consequentemente, área de dissipação de energia.
Laboratório de Física – UVV
6/15
Figura 3: Exemplo de um resistor de carbono de
Desta forma, para o resistor da Figura 3, seu Valor Nominal será
. Este é o valor
ajustado pelo fabricante e com a tolerância de
, o seu valor medido pode ser qualquer valor entre
3
, ou seja, qualquer valor entre
até
.
O Valor Nominal, e não o Valor Medido, é o valor empregado em projetos, utilizados na determinação
das correntes e tensões no circuito.
Os resistores estão arranjados em gavetas de uma caixa de miudezas, onde cada gaveta possui
resistores de uma mesma ordem de grandeza (mesma quarta faixa). Na Figura 4 a caixa de
resistores está aberta nos resistores de
(terceira faixa laranja). Cada nicho esta preenchido com
resistores de diferentes valores, como
,
,
,
,
e
.
Figura 4: Caixa de Resistores com a gaveta e ordem 10³
2.3. O Protoboard
Protoboard são pranchas empregadas na montagem de protótipos de circuitos para fins de testes e
projetos. O Laboratório de Física possui dois tipos de protoboard, o MP-2420 e o MP-1680A. Ambos
os protoboards são compostos por dois tipos de elementos, tipo A e tipo B como ilustra a Figura 5,
no entanto, dispostos em arranjos diferentes. Esta apresentação será focada no modelo Minipa MP2420.
Estes protoboards são compostos de dois tipos de elementos, marcados como A e B na Figura 5, e
3
Observe que a precisão da resistência dependerá da precisão do equipamento de medida empregado.
Laboratório de Física – UVV
7/15
quatro bornes coloridos, identificados no como terra, , ,
e 4, veja a Figura 5. Estes bornes
não estão conectados ao restante do protoboard, sua conexão deve ser feita com o emprego de fios
metálicos, como será apresentado adiante. Da mesma forma, os elementos tipo A e B não possuem
conexões entre si, sendo totalmente independentes. Para conectá-los eletricamente é necessário a
utilização de fios e dispositivos elétricos.
Figura 5: Protoboard Minipa MP-2420 (2420 pontos)
O protoboard MP-2420 possui três elementos do tipo A e 5 elementos do tipo B, enquanto que o
protoboard MP-1680A possui apenas 2 elementos do tipo A e 4 do tipo B. A disposição destes
elementos também diferem de um modelo para o outro, entretanto o seu funcionamento é o mesmo
em ambos os modelos.
O elemento tipo A possui 64 trilhas dispostas em duas linhas de 32 trilhas cada. Cada trilha, linhas
destacadas em verdes na Figura 6, possui 5 furos cada conectados verticalmente. Observe que as
32 trilhas da linha superior são completamente independentes das 32 trilhas na linha inferior.
Figura 6: Elemento tipo A: 64 trilhas com 5 pontos conectados cada.
Já o elemento do tipo B, é composto por 4 trilhas, onde cada trilha é composta de 25 furos,
eletricamente conectados, e agrupados em 5 colunas, veja as linhas em verde na Figura 7.
Figura 7: Elemento tipo B: 4 trilhas de 25 pontos conectados
2.3.1. Montando Circuitos no Protoboard
Em geral, a montagem de um circuito é mais confortavelmente realizada nos elementos do tipo A,
dado a sua disposição. Os elementos do tipo B são mais utilizados para levar um potencial elétrico a
pontos distantes do protoboard. Isto não significa que os elementos do tipo B não possam ser
usados na montagem do circuito, apenas não são convenientes para este serviço.
4
O modelo MP-1680A possui apenas três bornes
Laboratório de Física – UVV
8/15
Nas seções a seguir são apresentados algumas montagens de circuitos simples, ilustrando o
emprego do protoboard.
Atenção: Antes de iniciar o experimento na seção 3 realize todas as montagens das seções
seguintes: 2.3.2. Resistores em Série; 2.3.3. Resistores em Paralelo; e 2.3.4. Circuitos Mistos.
Demonstre as expressões (3), (4) e (5), calcule as resistências dos arranjos e compare com os
valores medidos. Ao final, apresente os resultados em uma folha avulsa para seu professor.
2.3.2. Resistores em Série
A Figura 8 apresenta um circuito simples com quatro resistores
associados em série. O primeiro passo na montagem do circuito
no protoboard é identificar os pontos de conexão entre dois ou
mais dispositivos. Estes pontos foram nomeados com as letras de
“ ” a “ ” no circuito da Figura 8. O primeiro ponto, letra “ ”,
representa a conexão entre o resistor
e o terminal positivo da
fonte , o ponto “ ” a conexão entre os resistores
e
,o“ ”
entre os resistores
e
, o “ ” entre
e
, e por fim, “ ”
entre o resistor
e o terminal negativo da fonte.
Cada conexão, pontos “ ” a “ ” no circuito da Figura 8, se tornará
uma trilha no protoboard. Uma possível montagem para este
circuito é apresentada na Figura 9.
Observe que cada ponto de conexão entre os dispositivos
ocupam uma das trilhas no protoboard.
Figura 8: Circuito Série
Figura 9: Montagem de quatro resistores em série.
Em verde estão evidenciados os trechos das trilhas por onde a corrente elétrica passaria, caso o
circuito fosse alimentado por uma fonte de tensão. Observe que a conexão poderia ter sido feita
na trilha em vermelho, sem qualquer problema na funcionalidade do circuito. Isto é possível pois a
trilha da conexão esta na linha superior do elemento tipo A e portanto está isolada das trilhas da
linha inferior, como é o caso da trilha em vermelho.
A resistência equivalente é calculada por aplicação direta da expressão (1), associação em série,
apresentada em seção anterior. Para o circuito da Figura 8, a resistência equivalente será dada pela
expressão:
(3)
2.3.3. Resistores em Paralelo
Um circuito com quatro resistores em paralelo é apresentado na Figura 10. Observe que neste
circuito exite apenas dois pontos onde os dispositivos são conectados, nomeados de “ ” e “ ”.
Todos pontos na parte superior do circuito correspondem a uma mesma conexão, “ ”, assim com na
Laboratório de Física – UVV
9/15
parte inferior, que corresponde a conexão “ ”. Observe que este é o mesmo caso da Figura 2-(a) e
(b) da seção 2.1.2. Associação em Paralelo.
Figura 10: Circuito Paralelo
Uma possível montagem no protoboard para este circuito é apresentado na Figura 11. As trilhas “ ”
e “ ” são marcadas em verde para evidenciar as conexões do circuito.
Figura 11: Montagem de quatro resistores em paralelo.
A resistência equivalente é calculada por aplicação direta da expressão (2), associação em paralelo,
apresentada em seção anterior. Para o circuito da Figura 10, a resistência equivalente será dada pela
expressão:
(4)
2.3.4. Circuitos Mistos
Para finalizar, considere o circuito misto apresentado na Figura 12, com quatro resistores. Os pontos
de conexão são evidenciados no circuito e nomeados como as letras
a . As conexões
e
são conexões especiais, chamadas de nós. Chamamos de nós todas as conexões que unem três ou
mais dispositivos em um circuito elétrico.
O nó conecta o polo positivo da fonte aos resistores
e . O nó conecta os resistores ,
e . A conexão conecta os terminais dos resistores
e , enquanto que a conexão conecta
os resistores
e
, já a conexão
liga a resistência
ao polo negativo da fonte, fechando o
circuito.
Laboratório de Física – UVV
10/15
Figura 12: Circuito misto com 4 resistores.
A Tabela 2 traz um resumo das conexões para a montagem deste circuito.
Conexão Conecta dispositivos
Nó
Nó
terminal positivo da fonte ao esquerdo do resistor
terminal direito do resistor
com o superior do
terminal inferior do resistor
ao direito do
terminal inferior do
ao terminal esquerdo do
e o superior do
e o direito do
terminal negativo da fonte ao terminal esquerdo do
Tabela 2: Conexões para o circuito da Figura 12.
Como este circuito possui 5 conexões, esta montagem deve ocupar 5 trilhas distintas no protoboard.
Uma possível montagem para este circuito é apresentado na Figura 13.
Figura 13: Montagem do circuito misto em protoboard.
As trilhas , , ,
e
estão evidenciadas em verde na Figura 13. Observe que uma boa
montagem é aquela que mantêm a disposição física dos resistores, semelhantes à do circuito
original.
A resistência equivalente para o circuito da Figura 12 é facilmente determinada por meio das
associações em série e paralelo, com o emprego das expressões (1) e (2), resultando na expressão
(5), a seguir.
(5)
3. Experimento
Os resistores estão guardados no laboratório em uma caixa de pesca com as resistências
guardadas em gavetas por ordem de grandezas diferentes. A primeira gaveta corresponde aos
resistores de ordem
, a segunda ordem
, a terceira ordem
e assim sucessivamente.
Escolha seis resistores de mesma ordem de grandeza, se possível diferentes, e preencha a Tabela 3
Laboratório de Física – UVV
11/15
com os seus Valores Nominais e os Valores Medidos pelo Ohmímetro:
Nominal
Tolerância
Medido
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
Tabela 3: Resistores selecionados.
Em seguida, associe os resistores conforme solicitado a seguir.
3.1. Associação em Série
Paras as montagens a seguir, utilize algarismos significativos para os cálculos com os valores
medidos (ou nominais) dos resistores. Estes cálculos são apenas para avaliação das grandezas a
serem medidas.
✔
Monte os seis resistores em série.
✔
Calcule o valor da resistência equivalente:
: __________
✔
Meça o valor da resistência equivalente com o Ohmímetro:
: __________
3.2. Associação em Paralelo
✔
Selecione quatro dos resistores e os monte em paralelo:
Resistores Selecionados: ____, ____, ____, ____
✔
Calcule a resistência equivalente:
: __________
✔
Meça a resistência equivalente:
: __________
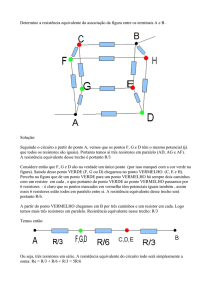
3.3. Associação Mista
✔
Copie os circuitos para as associações mistas apresentadas no quadro no espaço da Figura 14;
✔
Monte os circuitos no protoboard conforme os esquemas;
✔
Calcule a resistência equivalente, vista pelos terminais da fonte (
(b):
e
), para os circuitos (a) e
Laboratório de Física – UVV
12/15
Figura 14: Associações mistas
✔ Meça a resistência equivalente do circuito, vista pelos terminais A e B e preencha a Tabela 4.
Circuito
(a)
(b)
_______________ _______________
_______________ _______________
Tabela 4: Associações mistas
4. Resultados: Associação de Resistores
Utilizando a tolerância como incerteza, preencha a Tabela 5.
Resistor
Valores Nominais
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
Tabela 5: Resistências nominais empregadas.
Em seguida, com os valores nominais dos resistores, acima, calcule as resistências equivalentes dos
problemas e suas respectivas incertezas.
Laboratório de Física – UVV
Associações
Resistências Equivalentes
Série
____________
____________
Paralelo
____________
____________
Ccto Misto 1
____________
____________
Ccto Misto 2
____________
____________
Tabela 6: Resistores equivalentes para os circuitos.
13/15
Laboratório de Física – UVV
14/15
5. Experimento 01 – Associação de Resistores
Professor: ______________________________________ Turma: _____ Data: ___/___/20___
Alunos:
1: _____________________________________________________________________________
2: _____________________________________________________________________________
3: _____________________________________________________________________________
4: _____________________________________________________________________________
5: _____________________________________________________________________________
5.1. Dados Experimentais
Copie os dados das tabelas anteriores nas tabelas abaixo:
Nominal
Tolerância
Medido
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
____________
Tabela 7: Resistores selecionados, dados da Tabela 7.
Copie na Tabela 8 os dados relativos as resistências medidas e calculadas pelos valores nominais
nos experimentos.
Circuito
Série
Paralelo
Misto-a
Misto-b
_______________ _______________ _______________ ______________
_______________ _______________ _______________ ______________
Tabela 8: Associações Série, Paralelo e Mistos
Resistores Selecionados para a associação em paralelo: ____, ____, ____, ____
6. Equações e Expressões Relevantes
Nesta seção, são apresentados as expressões, equações e definições necessárias para o
desenvolvimento do experimento. O Formulário aponta as equações e definições essenciais para o
desenvolvimento das expressões na Composição, enquanto que este último apresenta as
expressões finais, geralmente, para a resolução do problema apresentado no experimento.
Laboratório de Física – UVV
15/15
6.1. Formulário
(6)
Associação de resistores em série
(7)
6.2. Composição
Este experimento não possui equação de composição pré definida, uma vez que os circuitos série e
paralelo são muito simples e os circuitos mistos são variáveis.
(8)
Resistência equivalente do circuito misto-a.
(9)
Resistência equivalente do circuito misto-b.