EXEMPLO 1 S: No sistema de polias ao lado, o bloco A se move

EXEMPLO 1
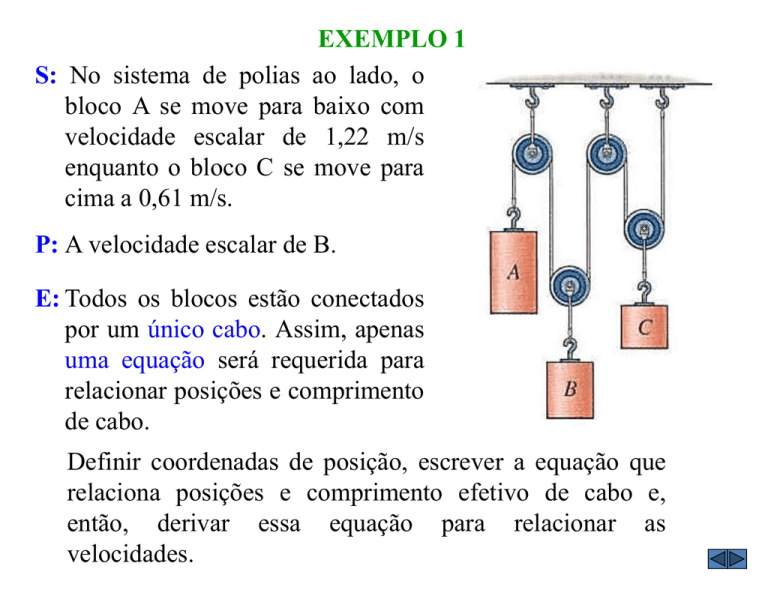
S: No sistema de polias ao lado, o
bloco A se move para baixo com
velocidade escalar de 1,22 m/s
enquanto o bloco C se move para
cima a 0,61 m/s.
P: A velocidade escalar de B.
E: Todos os blocos estão conectados
por um único cabo. Assim, apenas
uma equação será requerida para
relacionar posições e comprimento
de cabo.
Definir coordenadas de posição, escrever a equação que
relaciona posições e comprimento efetivo de cabo e,
então, derivar essa equação para relacionar as
velocidades.
EXEMPLO 1 (cont.)
Solução:
1) Uma linha de referência pode ser desenhada através das polias
superiores, sendo as coordenadas de posição definidas a partir
dessa linha até cada bloco (ou polia acima de cada bloco).
2) Definindo sA, sB, e sC como
indicado ao lado, a relação
de comprimento é tal que
sA + 2sB + 2sC = lE
3) Derivando para relacionar
as velocidades, tem-se que
vA + 2vB + 2vC = 0
 1,22 + 2vB + 2(– 0,61) = 0 e vB = 0 m/s !
EXEMPLO 2
S: Na figura ao lado, a polia em A é
puxada para baixo manualmente, com
velocidade escalar de 2,44 m/s.
P: A velocidade do bloco B.
E: Agora, há dois cabos envolvidos no
movimento desse sistema.
Assim, a posição de um ponto num
cabo deve ser relacionada à posição
do mesmo ponto no outro cabo.
Haverá duas equações, uma para cada
cabo em questão.
EXEMPLO 2 (cont.)
Solução:
1) Definir as coordenadas de posição a partir de uma linha de
referência fixa. Três coordenadas devem ser definidas: uma para o
ponto A (sA), uma para o bloco B (sB) e uma para relacionar
posições nos 2 cabos. Nota-se, nesse caso, que a polia C relaciona
o movimento dos dois cabos.
• Desenhar a linha de referência pela
polia superior (que é fixa).
• sA é definida até o centro da polia A.
• sB é definida até o centro da polia
que fica acima do bloco B.
• sC é definida até o centro da polia C.
• Todas as coordenadas são positivas
para baixo, ao longo das trajetórias.
EXEMPLO 2 (cont.)
2) Escrever as equações de comprimento efetivo para cada cabo.
Então, lE1 será o comprimento total
do 1º cabo menos a soma dos
trechos de comprimento constante,
enquanto lE2 será o equivalente
para o 2º cabo. Assim sendo,
cabo 1: 2sA + 2sC = lE1
cabo 2: sB + (sB – sC) = lE2
3) Eliminar sC entre as duas equações, donde resulta que
2sA + 4sB = lE1 + 2lE2
EXEMPLO 2 (cont.)
4) Relacionar as velocidades pela derivação da expressão acima.
Como lE1 e lE2 são constantes,
2vA + 4vB = 0
Portanto
vB = – 0,5vA = – 0,5(2,44)
= – 1,22 m/s
Ou seja, o bloco sobe a 1,22 m/s,
no sentido – sB .