Resoluções das atividades

FÍSICA 4
Resoluções das atividades
Aula 7
v (m/s)
Cinemática escalar – Movimento
uniformemente variado (MUV)
v
A2
Atividades para sala
A1
01 A
0
Nos pontos em que o gráfico da posição em função do
tempo é um segmento de reta inclinada, o movimento é
uniforme e a velocidade escalar é constante e não nula.
O sinal da velocidade escalar é dado pelo declive no gráfico do espaço, sendo positivo para função crescente e
negativo para função decrescente. Nos pontos em que o
gráfico da posição em função do tempo é um segmento
de reta horizontal, trata-se de repouso, e a velocidade é
nula. Nos pontos em que o gráfico da posição em função
do tempo é um arco de parábola, o movimento é uniformemente variado e a velocidade varia linearmente com o
tempo. Com esses argumentos, analisam-se os três gráficos da posição.
Gráfico 1: Até o 1 intervalo, o gráfico é um segmento de
reta decrescente, sendo a velocidade constante e negativa. No 2o intervalo, é um arco de parábola de declividade
decrescente que se liga a um segmento de reta horizontal,
indicando que o módulo da velocidade decresce até se
anular, levando-nos ao gráfico (c).
o
Gráfico 2: Até o 1 intervalo, o gráfico é um segmento de
parábola crescente, cuja declividade está diminuindo até
se ligar a um segmento de reta, também crescente, no 2o
intervalo, indicando que a velocidade é sempre positiva,
decrescente no 1o intervalo e constante no 2o intervalo,
levando-nos ao gráfico (d).
∆t1
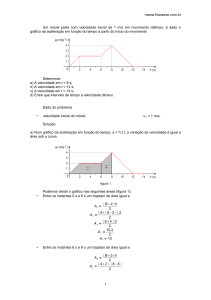
02 D
Cálculo da velocidade:
Dados: ∆S1 = 50 m; ∆S2 = 50 m.
Construindo o gráfico da velocidade em função do tempo
para os 10 segundos:
10
t (s)
∆t2
No gráfico da velocidade em função do tempo, a área
entre a linha do gráfico e o eixo dos tempos é numericamente igual ao espaço percorrido. Então:
v⋅t
v⋅t

⇒ 50 =
⇒ v ⋅ t = 100 (I)
 ∆S1 = A1 =
2
2

 ∆S2 = A 2 = v (10 − t ) ⇒ 50 = v (1
10 − t ) ⇒ 50 = 10 ⋅ v − v ⋅ t (II)
(I) em (II): 50 = 10v – 100 ⇒ v = 15 m/s
Cálculo da aceleração:
Aplicando a equação de Torricelli no trecho acelerado:
v2 = v 20 + 2 · a · ∆S1 ⇒ 152 = 02 + 2 · a · 50 ⇒ 225 = 100 · a ⇒
a = 2,25 m/s2.
03 B
Dados: ∆S = 130 + 80 = 210 m; v0 = 396 km/h = 110 m/s;
a = –5 m/s2
Aplicando a equação horária do espaço para movimento
uniformemente variado:
5
a
∆S = v 0 t + t 2 = 210 = 110 t − t 2 ⇒ t 2 − 44 t + 84 = 0 ⇒
2
2
t=2s
44 ± 1 936 − 336
⇒t =
⇒ t=2s
t=
t = 42 s (não convém)
2
o
Gráfico 3: Até o 1o intervalo, o gráfico é um segmento de
reta crescente, sendo a velocidade constante e positiva.
No 2o intervalo é um arco de parábola crescente, diminuindo a declividade até o vértice, indicando que a velocidade decresce até se anular. A partir daí, a função torna-se
decrescente, aumentando a declividade e indicando que
a velocidade se torna negativa, aumentando em módulo.
Essas conclusões levam-nos ao gráfico (b).
t
04 C
Calculando o módulo da aceleração escalar em cada caso:

 a1


 a2

∆v

a=
⇒  a3
∆t


 a4


 a5

Pré-Universitário – Livro 2
= 0 (v constante)
40 − 20
= 2 m/s2
10
0 − 10
=
= 5 m/s2
2
0 − 40
=
= 4 m/s2
10
20 − 100
=
= 2 m/s2
40
=
⇒ amáx = 5 m/s2
1
FÍSICA 4
movimento, o módulo da velocidade está aumentando (aceleração maior que zero), e, na segunda
parte, diminuindo (aceleração menor que zero).
Dessa forma, pode-se dizer que a aceleração não é
constante durante o movimento.
b) (F) Um movimento retilíneo uniforme tem aceleração
nula.
c) (F)Em momento algum do movimento descrito na
figura existe uma inversão de sentido do movimento. Logo, o carro não irá retornar à sua posição
inicial.
d)(V)
e) (F) Inverte o sentido de sua aceleração, e não do movimento (velocidade).
Atividades propostas
01 D
Tomando como unidade (u) o lado de cada quadrículo e
usando a propriedade do gráfico da velocidade × tempo,
as áreas dos trapézios fornecem as distâncias percorridas
por Encantado (dE) e Branca de Neve (d B):
5 +1

dE = 2 ⋅ 4 ⇒ dE = 12 u

d = 6 + 4 ⋅ 3 ⇒ d = 15 u
B
 B
2
⇒ dB > dE
02 B
05 A
v
A1
A2
A
Considerando desprezível a resistência do ar, a bola desce
em queda livre até que, em um determinado instante, ela
para abruptamente. Assim, a velocidade escalar aumenta
linearmente com o tempo, anulando-se instantaneamente;
enquanto a aceleração escalar é constante, até se anular,
também, instantaneamente, como mostram os gráficos da
alternativa A.
B
06 E
t0
t1
t2
t3
t4
t
t5
Inicialmente, o móvel B começa com maior velocidade
em relação ao móvel A. Portanto, como a distância percorrida representa a área sob a curva v × t, a área mais
clara representa a vantagem percorrida por B em relação
ao móvel A até o momento t2, quando as velocidades dos
dois móveis passam a ser iguais (área A1). A partir desse
momento, o móvel B desacelera e o móvel A acelera com
o mesmo módulo. Como os móveis acabam invertendo
as velocidades, o móvel A começa a percorrer maior
distância com o tempo, e a área mais escura representa
a vantagem de A em relação ao móvel B (área A2). Para
que os dois móveis se encontrem novamente, essas áreas
devem ser iguais, portanto, o encontro se dá no tempo t4.
03 E
O perito afirma: “Todo guiador profissional deveria aprender nos cursos de direção defensiva que a distância necessária para a completa parada de um veículo é, mantidas as
mesmas condições de frenagem, diretamente proporcional ao quadrado da velocidade que o veículo tem no início
∆S
∆S
da frenagem”. Portanto: 2 1 = 2 2 . Ou seja, se dobrar a
v1
v1
velocidade, a distância necessária será o quádruplo.
04 D
Analisando as alternativas,
a) (F) Em um movimento uniformemente variado, a aceleração é constante durante o movimento. O gráfico mostra claramente que, na primeira parte do
2
Distância (d) que o automóvel gasta para parar com velocidade inicial v:
v=0
v0 = v
v 2 = v 20 + 2 ⋅ a ⋅ d ⇒ 0 = v 2 + 2 ⋅ a ⋅ d ⇒ d =
v2
2⋅a
Distância (d') que o automóvel gasta para parar com velocidade inicial 2v:
v=0
v0 = 2v
4 ⋅ v2
v2 = v20 + 2 · a · d ⇒ 0 = (2v)2 + 2 · a · d' ⇒ d' =
2⋅a
v2
d=
2⋅a
4 ⋅ v2
d' =
2⋅a
d' = 4d
07 D
Na primeira situação, para o cálculo da aceleração do carro
com a pista seca, tem-se:
v2 = v02 + 2 · a · ∆S ⇒ 02 = 102 + 2 · a · 5 ⇒ a = –10 m/s2
Por sua vez, no cálculo da aceleração do carro com a pista
molhada, tem-se:
25
100
v2 = v02 + 2 · a · ∆S ⇒ 02 = 102 + 2 · a · 6 ⇒ a = −
= − m/s2
3
12
Na segunda situação, para o cálculo da distância percorrida com a pista seca, tem-se:
v2 = v02 + 2 · a · ∆S ⇒ 02 = 302 + 2 · (–10) · ∆S ⇒ ∆S = 45 m
Por sua vez, para o cálculo da distância percorrida com a
pista molhada, tem-se:
Pré-Universitário – Livro 2
FÍSICA 4
 25 
v2 = v02 + 2 · a · ∆S ⇒ 02 = 302 + 2 ·  −  · ∆S ⇒ ∆S = 54 m
3
Ou seja, a distância a mais é igual a d = 54 – 45 = 9 m.
08 D
A primeira figura permite concluir que, para menores temperaturas (motor frio) e em pista em aclive, a emissão de
CO é maior. A segunda figura mostra que essa emissão
é maior para baixas velocidades médias e em pista em
aclive.
09 B
Convertendo a velocidade para unidades do SI:
54
vM =
= 15 m/s
3, 6
4
Sendo o tempo de reação igual a , tem-se:
5
4
dR = 15 ⋅ = 3 ⋅ 4
5
dR = 12 m
10 E
A aceleração escalar é a = –5 m/s2
Aplicando a equação de Torricelli:
v 2 = v 20 +2 ⋅ a ⋅ ∆S ⇒ 0 = 252 − 2 ⋅ ( 5) ⋅ ∆S ⇒ ∆S =
625
⇒
10
⇒ ∆S = 62, 5 m
Pré-Universitário – Livro 2
3