formatação final M2-parte1

ATENÇÃO:
O material a seguir é parte de uma das aulas da apostila
de MÓDULO 2 que por sua vez, faz parte do CURSO
de ELETROELETRÔNICA ANALÓGICA -DIGITAL
que vai do MÓDULO 1 ao 4.
A partir da amostra da aula, terá uma idéia de onde o
treinamento de eletroeletrônica poderá lhe levar.
Você poderá adquirir o arquivo digital da apostila
completa (16 aulas), ou ainda na forma impressa que
será enviada por por correio. Entre na nova loja
virtual CTA Eletrônica e veja como:
www.lojacta.com.br
Além de ter a apostila e estuda-la, torne-se aluno e
assim poderá tirar dúvidas de cada uma das questões
dos blocos atrelados a cada uma das aulas da apostila,
receber as respostas por e-mail, fazer parte do
ranking de módulos e após a conclusão do módulo
com prova final, participar do ranking geral e poder
ser chamado por empresas do ramo de eletroeletrônica.
Saiba mais como se tornar um aluno acessando nossa
página de cursos:
www.ctaeletronica.com.br/web/curso.asp
APOSTILA ELÉTRICA-2 E ELETRÔNICA-1
MÓDULO - 2
AULA INDUTOR E CAPACITOR
EM CORRENTE ALTERNADA
2
Associação de indutores em série e paralelo
Capacitores em corrente alternada
A corrente no capacitor - reatância capacitiva
INDUTOR EM CORRENTE ALTERNADA
Até agora estudamos o indutor em circuitos de
corrente contínua, onde pudemos concluir, que
tendo correntes circulantes constantes sem
nenhuma variação, a reatância indutiva das
bobinas (indutores) era igual a zero, fazendo com
que estas bobinas se comportem como um “curto”
(resistência igual a zero), não gerando quedas de
tensões sobre essas.
Agora vamos estudar o que ocorre em circuitos
elétricos com indutores, que estejam submetidos a
correntes alternadas ou que variam no tempo.
Voltando à fórmula de reatância indutiva (XL) da
página 5, teremos:
XL = 2¶fL , portanto a reatância XL dependerá da
frequência da corrente do circuito. Como agora a
tensão é alternada, isso implica que a reatância
será diferente de zero e a nossa bobina começará a
se opor à corrente elétrica como se fosse um
resistor.
Se a nossa tensão alternada for de baixa frequência
(60 Hz por exemplo), a bobina funcionará como um
resistor de baixo valor (de 1 a 100W, dependendo do
valor da indutância L). Agora para as médias
frequências (1kHz por exemplo), a bobina
funcionará como um resistor de médio valor (de 1kW
a 10kW , dependendo da indutância) e para tensões
alternadas de alta frequência (1MHz, por exemplo)
a resistência equivalente será também muito alta.
Na figura 1a, temos um circuito com uma tensão
alternada de 10Vrms e uma frequência de 100Hz,
onde está ligada apenas uma bobina de 10mH (milihenry). Como a frequência é baixa podemos
concluir que a bobina deverá se comportar como
um resistor de baixo valor; para comprovarmos
isso, vamos pegar a fórmula da reatância indutiva e
figura 1a
GERADOR
10Vrms
100Hz
ELETRÔNICA
figura 1b
L1
10mH
GERADOR
10Vrms
100Hz
XL
6,3W
calcularmos o valor da reatância que irá se opor a
passagem de corrente:
XL = 2¶f L = 2 x 3,1416 x 100 x 0,01 = 6,3W
Portanto, o valor da reatância indutiva da bobina L1
num circuito de corrente alternada de 100Hz, será
de 6,3W. Vamos agora calcular a corrente “média”,
ou seja eficaz (Irms) do circuito. Devemos
primeiramente lembrar que os indutores, bem como
os capacitores, não são componentes lineares; isso
quer dizer que a tensão, a corrente e suas
resistências (ou reatância) não são proporcionais
entre si (nem inversamente proporcionais), portanto
a lei de Ohm não pode ser aplicada a estes
componentes. Contudo, em circuitos
“exclusivamente” compostos por indutores, sem
capacitores e sem resistores, existe uma lei básica,
derivada da lei de Ohm que pode ser aplicada a
estes circuitos e somente neste caso, trocando a
resistência elétrica (R) pela reatância indutiva (XL),
ficando com a seguinte relação:
Vrms = XL x Irms e Irms = Vrms / XL
Voltamos a lembrar que essa relação vale somente
para circuitos formado apenas por indutores. Isso
significa que se nosso indutor (bobina) tiver uma
resistência elétrica muito grande (devido ao
material de que ela é construída), ou mesmo se seu
capacitor “parasita” (devido as espiras paralelas) for
de valor expressivo, essa fórmula não poderá ser
aplicada.
Depois de todas estas considerações, podemos
finalmente calcular a corrente eficaz do circuito da
figura 1: Irms = Vrms / XL = 10V / 6,3W = 1,6 A
Pronto, já temos agora a corrente eficaz (Irms) do
circuito da figura 1, que é formado por um gerador
de tensão senoidal de 10Vrms e 100Hz de
frequência, que está ligado a uma bobina de 10mH,
gerará uma corrente alternada de 1,6 A, devido a
reatância indutiva dessa bobina valer 6,3W para
essa frequência (100Hz).
Vamos fazer um segundo exemplo com um circuito
similar ao da figura 1, mas alterando a frequência do
gerador e a indutância da bobina:
INDUTORES-REATÂNCIA INDUTIVA/CAPACITIVA-TRANSFORMADORES-FILTROS-SEMICONDUTORES-DIODOS-ZENERS-TRANSISTORES-AMPLIFICADORES DE SINAL-AMPLIFICADORES A,B,C
19
APOSTILA ELÉTRICA-2 E ELETRÔNICA-1
Neste segundo circuito (figura2), temos do lado
esquerdo, figura 2a, praticamente o mesmo circuito
da figura 1a, então podemos substituir a bobina L1
por sua reatância indutiva XL, que neste caso
poderá ser calculada como:
XL = 2 p f L = 2 x 3,14 x 1000000 x 0,00022 então:
XL = 1380W ou XL = 1,4kW.
Já na figura 2b temos o circuito da figura 2a,
substituindo a bobina L1 pela sua reatância XL,
neste caso também podemos aplicar a fórmula da
“nova lei de Ohm” para circuitos indutivos,
considerando que a resistência elétrica da bobina
L1 seja aproximadamente zero, onde teremos:
Irms = Vrms / XL = 10 / 1.400 = 7,1mA
Portanto, a bobina L1 produzirá uma corrente eficaz
de 7,1 mA, quando ligada a um gerador de tensão
alternada de 10Vrms com 1MHz de frequência.
figura 2a
GERADOR
10Vrms
1MHz
L1
220H
m
figura 2b
GERADOR
10Vrms
1MHz
XL
1,4kW
CONCLUSÃO
Os indutores (bobinas), em circuitos de corrente
alternada, farão oposição às variações de corrente
do circuito de acordo com suas reatâncias
indutivas, cujos valores dependerão da indutância
dessas bobinas, e principalmente das frequências
das correntes que circularão pelas bobinas.
Para correntes alternadas ou variáveis de baixa
frequência, a reatância indutiva das bobinas será
equivalente a resistores de baixo valor, quase não
se opondo à passagem das correntes do circuito
(conforme exemplo da figura 1).
Já para correntes alternadas ou variáveis de alta
frequência, a reatância indutiva das bobinas será
equivalente a resistores de alto valor, fazendo
grande oposição a passagem das correntes
elétricas, como pudemos observar no exemplo da
figura 2.
Caso o aluno queira saber mais detalhes sobre
circuitos de correntes alternada com indutores e
capacitores e ou resistores, ele poderá fazer uma
pesquisa em bibliotecas, ou então procurar na
internet informações sobre circuitos indutivos em
correntes alternadas, atraso de sinais e correntes, e
20
MÓDULO - 2
ainda análise de circuitos RLC.
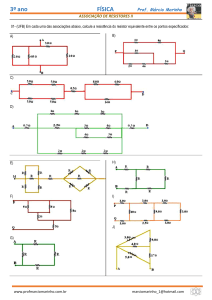
ASSOCIAÇÃO DE INDUTORES
Em certos circuitos, podemos nos deparar com dois
ou mais indutores ligados juntos, formando um
único indutor (indutor equivalente), para podermos
analisar circuitos assim devemos calcular os
valores desses indutores “equivalentes” em
associações de vários indutores.
Na apostila de Módulo 1, pudemos estudar a
associação de resistores e também de capacitores.
Nas associações de resistores em série o resistor
equivalente sempre será igual a soma algébrica
simples de todos os valores de sua resistências. Na
associação de resistores em paralelo foi
demonstrado um método simples de cálculo
envolvendo dois resistores de cada vez, calculando
o resistor equivalente a dois resistores em paralelo
e depois recalculando o próximo resistor paralelo,
até chegarmos a um único resistor equivalente a
essa malha paralela, levando sempre em
consideração a proporção entre os resistores.
Vimos também que nas malhas de resistores
paralelos de mesmo valor de resistência, o resistor
equivalente total dessa malha seria o valor de um
resistor dividido pelo números de resistores dessa
malha.
Na associação de capacitores em paralelo vimos
que o cálculo do capacitor equivalente seria o
mesmo para associação de resistores em série,
fazendo apenas a soma simples dos valores das
capacitância dos capacitores. Também na
associação de capacitores em série pudemos fazer
a mesma comparação com a associação de
resistores em paralelo, aplicando os mesmos
cálculos de resistores equivalentes para
capacitores equivalentes, à partir de dois
capacitores, até chegarmos a um capacitor
equivalente para toda a malha série. Pudemos ver
também uma fórmula para calcular diretamente o
capacitor equivalente de uma malha série, sem
precisar calcular de 2 em 2. Essa mesma fórmula
serve para calcular o resistor equivalente em uma
malha paralela formada por vários resistores de
valores diferentes.
Nas associações de indutores, fica claro que os
métodos de cálculo para achar o indutor
equivalente serão os mesmos aplicados para
resistores e capacitores, como mostraremos a
seguir:
ASSOCIAÇÃO EM SÉRIE
Na associação em série, teremos vários indutores
ligados um depois do outro, como mostra a figura
31, formando um único indutor equivalente.
A associação em série de indutores levará a um
valor final de indutância maior que o maior valor do
indutor associado. Isto porque na associação série,
INDUTORES-REATÂNCIA INDUTIVA/CAPACITIVA-TRANSFORMADORES-FILTROS-SEMICONDUTORES-DIODOS-ZENERS-TRANSISTORES-AMPLIFICADORES DE SINAL-AMPLIFICADORES A,B,C
ELETRÔNICA
APOSTILA ELÉTRICA-2 E ELETRÔNICA-1
as indutâncias dos indutores associados irão se
somar.
Para que possamos calcularmos este valor, basta
somar os valores dos indutores associados e
chegaremos ao resultado final. Uma analogia pode
ser feita com o cálculo de resistência equivalente de
resistores ligados em série. Um exemplo disso pode
ser visto na figura 3.
figura 3
A
A
Apesar desta fórmula apresentada na figura 5
fornecer meios para o cálculo de indutores em
paralelo (já apresentada no módulo1 para cálculos
de capacitores em série), lembramos que o meio
mais rápido e prático de se calcular indutores
equivalente é o método utilizado para cálculo de
resistores em paralelo.
Para exemplificar melhor, vamos pegar um exemplo
de 3 “bobinas” em paralelo, como na figura 6:
Na figura 6, podemos ver 3 indutores (L1,L2 e L3)
ligados em paralelo entre os pontos “A” e “B”;
B
Leq
MÓDULO - 2
figura 6
A
B
A
A
Leq
Leq = L1 + L2 + L3 +...+ Ln
B
Para fixar o método vamos pegar um exemplo de 3
indutores em série, como mostra a figura 4.
figura 4
L1=10m H
Leq
47mH
L2
22mH
B
B
L3=15mH
Nesta figura (4) podemos ver L1, L2 e L3 em série
entre os pontos “A” e “B”. Este método de cálculo
para encontrar o indutor equivalente na malha série
é o mesmo utilizado em resistores série, bastando
somar os valores das indutâncias dos indutores,
ficando então com: Leq = L1 + L2 + L3, onde
substituindo, teremos Leq = 10mH + 22mH + 15mH,
resultando Leq = 47mH.
ASSOCIAÇÃO EM PARALELO
Nesse tipo de associação, devido a corrente dos
indutores estar sendo dividida, teremos um
resultado de indutância menor que o menor valor do
indutor em paralelo. Para que possamos calcular
este valor, façamos o cálculo da figura 5 ou
utilizamos do mesmo cálculo feitos nas associação
paralelas dos resistores, vistos na apostila de
módulo 1.
figura 5
A
A
L2
L3
L4
Ln
B
Leq
B
1
1
1
1 ... 1
=
+
+
+ +
Leq L1 L2
L3
Ln
ELETRÔNICA
L
L3
5mH 20mH
B
Leq
4mH
A
A
L1
L1
L2
L3
10mH 10mH 20mH
B
poderíamos utilizar a fórmula indicada na figura 5,
mas para melhor compreensão da aplicação do
mesmo cálculo utilizado com resistores, vamos
aplicar o método de associação de resistores
paralelos.
Em associação de indutores em paralelo utilizamos
o mesmo cálculo de resistores paralelos.
Voltando então a figura 6, vamos utilizar o método
de resistores paralelos. Primeiro, achamos o
indutor equivalente a 2 indutores (L1 e L2). Como L1
e L2 são iguais o indutor equivalente terá a metade
do valor de cada indutor então: L = L1/2 = 5mH.
O próximo passo, será substituir L na malha
paralela, como mostra o circuito do meio da figura 6;
como sobraram ainda 2 indutores (L e L3), devemos
calcular novamente o indutor equivalente. O indutor
de menor indutância é L (5mH) ficando com 1x, e L3
valerá proporcionalmente 4x, totalizando 5x. Agora
dividindo o indutor de maior (L3) por 5x, chegando
ao valor Leq = 4mH.
Para confirmar se o cálculo pela fórmula da figura 5
estaria correto, vamos refazer os cálculos, só que
agora aplicando a fórmula:
1/Leq = 1/L1 + 1/L2 + 1/L3, ficando neste caso com
1/Leq = 1/10 + 1/10 + 1/20 = 1/Leq. Depois de
reduzida as frações ao mesmo denominador
teremos 1/Leq = 2/20 + 2/20 + 1/20 = 5/20 = 1/Leq.
Agora invertendo as frações: Leq/1 = 20/5 = 4mH =
Leq.
Como observa-se, os 2 métodos de cálculo de
indutores em paralelo são equivalentes e chega-se
ao mesmo resultado. Queremos aqui novamente
salientar que a fórmula da figura 5, também pode
ser aplicada a associação de resistores em
paralelo, bastando substituir os indutores da
fórmula por resistores:
1/Req = 1/R1 + 1/R2 + 1/R3 + ... + 1/Rn
INDUTORES-REATÂNCIA INDUTIVA/CAPACITIVA-TRANSFORMADORES-FILTROS-SEMICONDUTORES-DIODOS-ZENERS-TRANSISTORES-AMPLIFICADORES DE SINAL-AMPLIFICADORES A,B,C
21
APOSTILA ELÉTRICA-2 E ELETRÔNICA-1
CAPACITOR EM CORRENTE ALTERNADA
Na apostila de módulo 1, estudamos o capacitor, um
componente elétrico que tem a função de
armazenar cargas elétricas, mas nosso estudo se
limitou a capacitores ligados em tensão contínua.
Com isso pudemos verificar que um capacitor
ligado a uma tensão contínua irá se carregar com
aproximadamente a mesma tensão de alimentação
e depois irá permanecer carregado, como se fosse
uma bateria, sem permitir que exista corrente
circulante por ele; podemos então comparar um
capacitor carregado, com uma chave aberta.
figura 7
R1
GERADOR
DE TENSÃO
ALTERNADA
C1
Agora, vamos começar a estudar o comportamento
do capacitor quando ligado a uma tensão alternada.
Inicialmente vamos tomar um circuito formado por
um gerador de corrente alternada senoidal, onde
vamos ligar um resistor R1 em série com um
capacitor C1, conforme a figura 7:
Nesta figura, podemos observar que o capacitor C1
está em série com o resistor R1 e portanto toda
corrente que irá “carregar” o capacitor C1
obrigatoriamente também irá passar por R1. Vamos
chamar de Vg, a tensão senoidal gerada por nosso
figura 8 gerador, sendo a
+Vmax
forma de onda desta
tensão, vista na
0V
Vg
figura 8:
-Vmin Essa tensão gerada
se caracteriza por ser
uma tensão senoidal
e principalmente por ser uma tensão alternada, ou
seja numa parte do ciclo ela é positiva, gerando
corrente circulante que vai do gerador até a
“massa”, passando primeiramente por R1 e depois
carregando C1; na outra metade do ciclo ela é
negativa, gerando corrente inversa que tem o
sentido da “massa” para o gerador, que irá
descarregar o capacitor e passar por R1 e
finalmente terminando no gerador.
Toda tensão alternada, seja senoidal ou não, irá ter
essa característica: uma parte do ciclo será
positivo, gerando corrente no sentido do gerador à
“massa”, e o restante do ciclo será tensão negativa,
gerando corrente no sentido da “massa” para o
gerador.
Baseado nessas conclusões, podemos a partir da
+
22
-
MÓDULO - 2
tensão gerada pelo gerador (Vg) calcularmos a
forma de onda da tensão “acumulada” no capacitor
C1. Vamos chamar essa tensão no capacitor C1 de
Vc. Essa tensão deverá ter a forma de onda similar
a forma de onda gerada figura 9
Tb
Ta
To
Tf
Vg, mas sua amplitude
+Vp
máxima (+Vp) e sua
+ T3 T4 T5
amplitude mínima (-Vp)
Vg T1I T2I I I I
deverão ser menores
-Vp
que as tensões máxima
+Vp
e mínima do gerador
+I I T4I T5I
(+Vmax e -Vmin).
I
Vamos considerar a Vc T1 T2 T3
-Vp
forma de onda da figura
9, como sendo a
comparação entre a forma de onda do gerador Vg e
a forma de onda no capacitor Vc:
A forma de onda de cima corresponde à tensão
gerada Vg pelo gerador; T1 corresponde ao tempo
inicial quando ligamos o gerador e o capacitor ainda
está descarregado; T2 corresponde ao tempo no 1°
ciclo em que a tensão Vg atinge a tensão máxima
(+Vmax); T3 corresponde ao tempo onde no 1° ciclo
a tensão Vg vale zero volt e irá mudar para o ciclo
negativo invertendo a tensão; T4 é o tempo onde no
1° ciclo a tensão Vg atinge o máximo negativo (Vmin) e finalmente T5 é o tempo onde a tensão Vg
volta a valer zero volt encerrando o 1° ciclo e
recomeçando tudo novamente.
A forma de onda de baixo na figura 9, corresponde a
tensão Vc no capacitor C1: em T1 temos o instante
que é ligado o gerador e a tensão Vc ainda é igual a
zero volt, pois o capacitor está descarregado; no
instante T2 apesar de ser o pico de tensão no
gerador (+Vmax) a tensão no capacitor ainda não é
máxima, pois para o capacitor se carregar é
necessário que exista uma corrente I que levará as
cargas até a placa do capacitor, e essa corrente I
quando passar por R1 irá gerar uma queda de
tensão Vr sobre R1 então teremos uma tensão
sobre C1 (Vc) menor que Vg, como podemos ver na
figura 10:
Como é visto na figura 10, a tensão Vg irá gerar uma
corrente I circulante que irá carregar C1 com uma
tensão Vc; essa mesma corrente I irá gerar uma
queda de tensão Vr sobre R1, então podemos dizer
-
-
figura 10
Vr
R1
I
Vg
Vc
INDUTORES-REATÂNCIA INDUTIVA/CAPACITIVA-TRANSFORMADORES-FILTROS-SEMICONDUTORES-DIODOS-ZENERS-TRANSISTORES-AMPLIFICADORES DE SINAL-AMPLIFICADORES A,B,C
C1
ELETRÔNICA