a evolução do universo - Universidade da Madeira

GRUPO DE ASTRONOMIA
DA
UNIVERSIDADE DA MADEIRA
A EVOLUÇÃO DO UNIVERSO
ANGELINO GONÇALVES
ORLANDO SILVA
SEGUNDA SEMANA DA ASTRONOMIA
18 DE JULHO DE 2002
COSMOLOGIA
DO BIG BANG AO BIG CRUNCH
INTRODUÇÃO
OBSERVAÇÕES CRITÍCAS
ELEMENTOS LEVES
HOMOGÉNIEDADE E ISOTROPIA
O ABC... DO CALCULO DE DISTÂNCIAS
DIAGRAMAS ESPAÇO-TEMPO
FACTOR ESCALA a(t)
CURVATURA ESPACIAL
O PROBLEMA VELHICE-ACHATAMENTO
MANIPULANDO OS DIAGRAMAS ESPAÇO-TEMPO
O PROBLEMA DO HORIZONTE
INFLAÇÃO
A ESTRUTURA DE GRANDE ESCALA E A ANISOTROPIA
INTRODUÇÃO
Até há muito pouco tempo o Sistema Solar e o Universo
eram considerados como sendo a mesma coisa nas
mentes dos cientistas, de tal forma que a descoberta de
que a Terra não era o centro do Sistema Solar constituiu
um passo importante no desenvolvimento da
COSMOLOGIA.
No ínicio do século 20, Shapely demonstrou que o
Sistema Solar está muito longe do centro da Via Lactea.
Por esta razão em 1920 o palco estava pronto para as
descobertas observacionais que nos levaram à
TEORIA DO BIG BANG
OBSERVAÇÕES CRITÍCAS
Dados de Hubble (1929). O declive da linha é de
464 Km/seg/Mpc,
e é conhecida como a constante de Hubble, H0.
(1 Mpc = 3.086E24 cm)
Por isso o valor da constante de Hubble é aproximadamente
2 Gyr.
Isto deve ser próximo da idade do Universo, e sabemos que a
idade da Terra é superior a 2 mil milhões de anos.
O valor de Hubble levantou muitas dúvidas sobre os modelos
cosmológicos e levou ao aprecimento do modelo do
ESTADO ESTÁTICO.
Devido a isto algums ciêntistas propuseram leis de Redshift ao
quadrado-Distância. Estudos feitos posteriormente revelaram que ele
tinha confundido dois tipos de Cefeides para calcular as distâncias.
Os dados de Hubble de 1929 eram de facto muito pobres.
O grafíco acima é uma confirmação dramática da lei de Hubble.
Os dados são de 1996 para Sne do tipo Ia.
O Redshift é definido de tal forma que:
1+z = λ(observado)/ λ(emitido)
A lei do Redshift-Distância descoberta por Hubble é
compatível com o ponto de vista de Copérnico, ou seja, a nossa
posição no Universo não é especial.
A velocidade de retrocesso é simétrica.
Consideremos agora os diagramas Espaço-Tempo
Este diagrama mostra varias Galáxias próximas a se afastarem de
nós quando observamos do nosso ponto de vista
(Galáxia A em cima, Galáxia B em baixo).
Os diagramas vistos dos dois pontos de vista são idênticos
excepto nos nomes das Galáxias.
Por outro lado a lei quadrática transforma-se numa lei não
quadrática anisotrópica quando mudamos os pontos de vista.
Se observassemos uma lei velocidade quadrática-distância, então
um observador noutra Galáxia iria ver uma lei diferente.
Portanto ou a lei Redshift-Distância é linear
ou nós estamos no centro do Universo.
No seguinte diagrama temos à esquerda um padrão homogénio
mas não isotrópico e à direita um padrão isotrópico mas não
homogénio.
Se uma figura é isotrópica a partir de mais do que um ponto
então ela também tem de ser homogénia.
É claro que o Universo não é homogénio e isotrópico, porque
contém regiões densas como a Terra, mas pode ser
estatisticamente homogénio e isotrópico.
Peacock e Dodds olharam para as flutuações de densidade no
Universo próximo e descobriram que para regiões de 100 Mpc o
Universo é liso dentro de uma pequena percentagem.
A hípotese de um Universo isotrópico e homogénio aumentou a
partir do momento em que Penzias e Wilson anunciaram a
descoberta das microondas cósmicas em 1965.
Eles observaram um excesso de fluxo com um comprimento de
onda de 7.5 cm equivalente à radiação de um corpo negro a
3.7 +/- 1 grau Kelvin.
Neste momento os melhores dados sobre o espectro da radiação
de fundo vem do instrumento FIRAS do satélite COBE.
Os pontos são consistentes com a radiação de um corpo negro
com a temperatura igual a 2.725 K.
A temperatura da radiação cósmica de fundo é quase igual por
todo o céu.
Este mapa tem uma escala de temperatura onde
0 K é preto e 3 K é branco
ELEMENTOS LEVES
Outra evidência a favor do Big Bang é a abundância de
elementos leves, tais como o hidrdrgénio, deutério (hidrogénio
pessado), hélio e lítio. Quando o Universo tinha apenas alguns
minutos de vida a temperatura era suficientemente alta para
construir elementos leves por fusão nuclear.
A teoria do Big Bang núcleo-síntese prevê que aproximadamente
1/4 da massa do Universo devia ser composta por hélio, o que é
muito próximo ao que é observado.
HOMOGENEIDADE E ISOTROPIA
Principio Cosmológico:
O Universo é Homogénio e Isotrópico
Para que possamos dizer que o Universo é homogénio implica
que qualquer propriadade do Universo é igual por todo o lado.
Isto só é parcialmente verdade, mas parece ser uma excelente
aproximação quando tomamos a média sobre grandes escalas.
O ABC... DO CALCULO DE DISTÂNCIAS
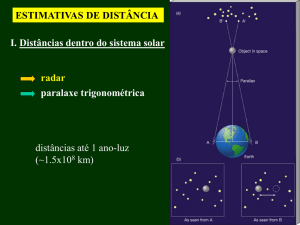
A) Paralaxe trigonométrica
B) Movimento de Enxames
C) Paralaxe secular
D) Paralaxe estatistico
E) Distância cinemática
F) Paralaxe de expansão
G) Distância do echo da luz
H) Binários visuais espectroscópicos
I) Método de Baade-Wesselink
J) Eclipses de binários espectroscópicos
K) Método de expansão da fotoesfera
L) da sequência principal
M) Paralaxe espectroscópico
N) Distância RR Lyrae
O) Distância das Cefeides
P) Função de luminosidade de Nebulosas Planetárias
Q) Estrelas mais brilhantes
R) Diametros das regiões mais largas de H II
S) Flutuações do brilho de superfície
T) Supernovas do Tipo Ia
U) Relação Tully-Ficher
V) Relação Faber-Jackson
W) Enxames das Galáxias mais brilhantes
X) Atraso do tempo em lentes gravitacionais
Y) Efeito Sunyaev- Zeldovich
Z) Lei de Hubble
A) Paralaxe trigonométrica
Método padrão, por excelência, para cálculo de distâncias
astronómicas
O paralaxe de uma estrela é metade do ângulo na estrela no
diagrama. Por isso o paralaxe é o ângulo formado na estrela no
triângulo Terra-Sol-estrela.
B) Movimento de Enxames
Não existem muitas estrelas próximas da Tera onde se possem
usar com sucesso o método anterior. Mas quando as estrelas
encontram-se num aglomerado estável cujo tamanho físico não
varia, como o enxame das Pleiades, então o movimento aparente
das estrelas dentro do enxame, pode ser utilizado para determinar
a distância a que se encontram.
C) Paralaxe secular
Método que pode ser utilizado para calcular distâncias
médias até um conjunto de estrelas, escolhidas por estarem
todas +/- à mesma distância da Terra.
I) Método de Baade-Wesselink
Baade-Wesselink
Método aplicado I)a Método
estrelasdepulsantes,
utilizando a cor e curvas do
fluxo da luz.
Desta forma encontrmos a razão entre os raios da estrela em
instantes de tempo diferente
M) Paralaxe espectroscópico
Quando o espectro de uma estrela é cuidadosamente observado,
é possível determinar dois parametros essencias da estrela assim
como a abundancia de subtâncias químicas na sua atmosfera.
1) Temperatura à superfície da estrela, responsável pelo tipo de
espectro que vai da mais quente à mais fria (OBAFGKM).
2) Gravidade à superfície da estrela.
O utilização do valor da gravidade à superfície para determinar a
luminosidade de uma estrela depende de três relações:
O) Distância das Cefeides
Cefeides são estrelas pulsantes devido às zonas de hidrogénio e
hélio ionizadas estarem perto da superfície da estrela.
Isto faz com que a temperatura da estrela seja +/- fixa e produz
uma faixa de instabilidade no diagrama H-R.
A sequência mostra a estrela a arrefecer e crescer e depois
diminuir e aquecer.
Uma vez que as Cefeides estão aproximadamente todas à mesma
temperatura, o tamanho de uma Cefeide determina a sua
luminosidade.
U) Relação Tully-Ficher
A velocidade rotacional de uma Galáxia espiral é um indicador
sua luminosidade.
A relação é aproximadamente
X) Atraso do tempo em lentes gravitacionais
Quando um quasar é detectado através de uma lente gravitacional
surgem multiplas imagens, como podemos ver no diagama.
Os caminhos da luz do Quazar até nós, que formam estas imagens,
tem comprimentos diferentes que diferem aproximadamente por
Y) Efeito Sunyaev- Zeldovich
Nuvens de gás quente envolvendo enxames de Galáxias,
provocam a distorção do espectro das microondas cósmicas de
fundo. Os electrões quentes no enxame de Galáxias dispersão
uma pequena fracção dos fotões do CMB e repõem-os por fotões
de enegia ligeiramente superior.
A altas frequencias o enxame aparente ser mais brilhante do que
o plano de fundo. Este efeito é proporcional a:
1) Densidade de electrões
2) Espessura do enxame ao longo da nossa linha de visão
3) Temperatura dos electrões
O parâmetro que combina estes factores disigna-se por parâmetro
Y-Kompaneets
A emissão de raios-X, Ix, da nuvem de gás do enxame é
proporcional a:
1) Quadrado da densidade de electrões
2) Espessura do enxame ao longo da nossa linha de visão
3) Temperatura dos electrões e frequencia de raios-X
Como resultado obtemos a razão
DIAGRAMAS ESPAÇO-TEMPO
Diagrama Espaço-Tempo da Terra a andar à volta do Sol. Aqui
tentamos utilizar perspectiva para tentar mostrar duas
dimensões, mas normalmente mostramos apenas um eixo
espacial e evitamos perspectiva.
A linha que representa a posição da Terra como uma função do
tempo é chamada a linha do Universo. O declive da linha do
Universo para uma partícula mostra a sua velocidade em relação
ao referêncial do diagrama.
Este diagrama mostra partículas com várias velocidades
Devido à velocidade da luz ser especial na relatividade, os
diagramas Espaço-Tempo são muitas vezes desenhados em
unidades de segundos de luz ou anos de luz. Por isso um declive
unitário (ângulo de 45º) corresponde à velocidade da luz
O conjunto de todas as linhas do Universo à velocidade da luz
que passam por um evento definem os cones de luz daquele
evento: o cone de luz do passado e o cone de luz do futuro.
Com a correcta interpretação das variáveis, a Lei de Hubble, é
verdadeira para todos os valores de D, até os muito grandeds que
dão v > c.
Os cones de luz para Galaxias distantes estão virados para além
da vertical, indicando v > c.
Modelo de densidade zero feito utilizando D e t da lei de Hubble.
As linhas do Universo para observadores comoveis estão
desenhadas e decoradas com pequenos cones de luz. A linha
vermelha forma o nosso cone de luz do passado.
Diagrama Espaço -Tempo nas coordenadas especiais
relatívisticas x e t:
As hipérbolas cinzentas mostram as superfícies do tempo próprio
constante desde o Big Bang. Podemos ver que o nosso cone de
luz atravessa as linhas do Universo das Galáxias mais distantes
na distância especial relativistica
x = c*t/2.
As relações entre distância e velocidade na lei de Hubble e o
redshift são
v = Ho*D
D = (c/Ho) ln(1 + z)
1 + z = exp (v/c)
Note que a lei Redshift-Velocidade anterior não é a lei do desvio
especial relativistico de Doppler
1 + z = sqrt ((1 + v/c)/(1 - v/c))
que só se aplica às coordenadas relativisticas especiais, não a
coordenadas cosmológicas.
FACTOR ESCALA a(t)
Porque a velocidade ou dD/dt é exactamente proporcional a D, a
distância entre qualquer par de objectos comoveis cresce por um
factor (1 + H*dt) durante um intervalo de tempo dt.
DG(t) = a(t)*DG(t0) ⇒ a(t0) = 1
Para ρ menor que ou igual à densidade crítica ρ(crit), o Universo
expande para sempre, enquanto para ρ maior que ρ(crit) o
Universo vai eventualmente parar e implodir. O valor de ρ(crit)
para H0 = 65 Km/seg/Mpc é de 8E-30 gm/cc ou seja 5 protões
por metro cúbico.
Se a densidade estiver perto do valor crítico a maior parte da
matéria deve ser muito escura para ser observada. As estimativas
mais recentes sugerem que a densidade está entre 0.3 e 1 vezes o
ρ(crit).
CURVATURA ESPACIAL
Uma das consequências da relatividade geral é que a curvatura
do espaço depende da relação entre ρ e ρ(crit).
Chamamos a esta relação
Ω = ρ/ρ(crit).
Ω = 1, o Universo tem uma geometia Euclideana ou plana.
Ω > 1, o Universo tem curvatura positiva ou geometria esférica.
Ω < 1, o Universo tem curvatura negativa ou geometria hiperbólica.
H0 = 65 Km/seg/Mpc
Ω0 = 0 (linha verde) 15Gyr
Ω0 = 1 (linha preta) 10 Gyr
Ω0 = 2 (linha vermelha) 8.6 Gyr
O PROBLEMA
VELHICE-ACHATAMENTO
Se a densidade fosse ligeiramente alta o Universo morreria cedo,
num Big Crunch. Isto é conhecido como o problema da "velhice"
na Cosmologia. E porque um Universo de densidade crítica tem
geometria espacial "achatada", tambem é conhecido como o
problema do "achatamento".
MANIPULANDO OS DIAGRAMAS
ESPAÇO-TEMPO
As linhas do Universo são agora curvadas devido à força
gravitica que causa a desaceleração da expansão (Ω = 1).
Às vezes é conveniente dividir a expansão do Universo em
partes. O resultado no diagrama Espaço-Tempo é a divisão das
coordenadas espacias por a(t).
Esta expansão expandiu o nosso cone de linhas passadas e temos
que voltar a desenhar para mostrar tudo.
Esticando o eixo do tempo perto do Big Bang obtemos
Diagrama Espaço-Tempo Conformal
O diagrama Espaço-Tempo para Ω0 = 1 é infinito em extensão e
por isso o diagrama Espaço-Tempo Conformal pode extender-se
muito para além do nosso cone de luz do passado.
Outras coordenadas também podem ser utilizadas.
Neste diagrama a(t) serve como coordenada radial (Ω0 = 2)
O PROBLEMA DO HORIZONTE
O Universo era opaco antes dos electrões e protões se terem
combinado para formar átomos de hidrogénio quando T < 3 000
K a um redshift de 1 + z = 1 000. Após este momento os fotões do
CMB podiam movimentar-se livremente pelo Universo
transparente que hoje observamos
A temperatura num certo ponto do céu tinha de ser determinada
quando os átomos de hidrogénio se formaram (recombinação mesmo que tenha sido a primeira vez).
Como os comprimentos de onda do CMB expandiram da mesma
forma que as distâncias entre as Galáxias durante a expansão do
Universo, sabemos que a(t) era 0.001 quando se deu a
recombinação.
Para o modelo de Ω0 com t0 = 10 Gyr o tempo anda à volta de
300 000 anos depois do Big Bang. Isto é uma fracção tão
pequena da idade actual que é útil ampliar esta parte da historia
do Universo no diagrama Espaço-Tempo Conformal.
Estas regiões não têm eventos em comum, mas as duas
temperaturas são iguais até 1 parte em 10 000. Como é que isto é
possível? Isto é conhecido como o problema do "horizonte" em
Cosmologia.
INFLAÇÃO
A inflação oferece uma solução ao problema
"velhice-achatamento" e ao problema do "horizonte".
O cenário inflacionário invoca uma densidade energética do
vácuo. Na teoria dos campos quânticos, o vácuo não é vazio, mas
está cheio de partículas virtuais.
Podemos ver neste diagrama Espaço-Tempo a formação de
partículas-antipartículas do nada e que depois se anulam
novamente para o nada.
A desidade energética do vácuo produz uma "gravidade
repulsiva" que causa a expansão do Universo a acelerar em vez
de desacelerar, e isto aumenta o t0 para um dado H0.
O cenário inflacionário propõe que a energia do vácuo foi muito
grande durante um breve período na historia inicial do
Universo.Quando o Universo é dominado por uma densidade
energética do vácuo o factor escala cresce exponencialmente,
a(t) = exp (H(t0-t))
Por isso a constante de Hubble é verdadeiramente constante
durante esta época por isso não tem que ser zero.
Se a época inflacionária durar o tempo sufficiente a função
exponencial fica muito grande. Isto faz a(t) muito grande, o que
torna o raio de curvatura do Universo muito grande.
A seguir podemos ver o nosso horizonte sobreposto numa esfera
com um raio muito grande
ou numa esfera mas pequena
Como só podemos ver até ao horizonte, para o caso inflacionário
em cima a esfera de raio grande parece quase achatada para nós.
Isto resolve o problema "velhice-achatamento" desde que o
crescimento exponencial durante a época inflacionária se dobre
sobre si pelo menos 100 vezes. A inflação também resolve o
problema do "horizonte", porque o cone de luz do futuro de um
evento acontece antes que a inflação se tenha expandido para uma
região enorme pelo crescimento durante a inflação.
Neste diagrama Espaço-Tempo podemos ver a época de inflação
em verde, e os cones-de-luz do futuro de dois eventos em
vermelho.
A ESTRUTURA DE GRANDE ESCALA
E A ANISOTROPIA
É claro que o Universo não é realmente homogénio, porque
contém regiões densas como Galáxias e pessoas. Estas regiões
deviam de afectar a temperatura da radiação cósmica de fundo.
O potencial gravitacional
φ = -GM/r,
será negativo em regiões muito densas, e positivo em regiões de
menor densidade. Fotões perdem energia quando eles saiem dos
poços de potencial gravitacional das regiões mais densas.
No seguinte diagrama Espaço-Tempo Conformal os bocados
densos de materia aparecem como barras cizentas verticais, a
época antes da recombinação como a região tracejada, e o
potencial gravitacional como a curva multicolor φ(x).
Onde o nosso cone de luz intercepta a superfície de
recombinação, vemos a temperatura perturbada por
dT/T = φ/(3*c2).
A primeira anisotropia a ser detectada foi a anisotropia dipolar
em 1969
Este mapa é do COBE e tem melhor detecção do que o desvio
feito em 1969.
Este mapa mostra a anisotropia cósmica depois do padrão dipolar
e a radiação da Via Láctea ter sido subtraída.
A inflação prevê um certo padrão estatístico na anisotropia. As
flutuações quânticas afectam normalmente pequenas regiões,
mas a enorme expanção exponencial durante a época
inflacionária fez estas pequenas regiões observáveis.
Uma vez que o padrão observado da anisotropia é consistente
com a inflação, podemos também perguntar se esta amplitude
implica forças suficientemente grandes para produzir os
aglomerados de Galáxias que observamos.
Este diagrama Espaço-Tempo Conformal mostra φ(x) no
momento de recombinação, utilizando os dados dT obtido por
COBE, as linhas do Universo que estão perturbadas pelas forças
gravitacionais produzidas pelo gradiente de potencial.
No entanto o COBE não pode observar pontos do tamanho de
Galáxias ou até super enxames de Galáxias, mas se utlizarmos
"uma potência igual para todas as escalas" podemos extrapolar a
informaçã para escalas mais pequenas.
Desta forma descobrimos que as forças gravitacionais são
suficientemente grandes para produzir os enxames observáveis,
mas só se as forças não forem contrariadas por outras forças.
Podemos então concluir que a maior parte da matéria no Universo
é "matéria escura" que não emite, absorve ou dispersa a luz. Esta
estranha conclusão pode ser reforçada se os dados de escalas
ângulares mais pequenas que vão ser fornecidos pelo "Microwave
Anisotropy Probe" (MAP) que foi lançado no ano 2000.
INTERROGAÇÕES
Quais os tipos de matéria e energia que compõem o nosso Universo?
Qual é a percentagem de cada?
Qual é a velocidade de expansão do Universo neste momento?
Qual é a idade do Universo neste momento?
Que tipo de Universo é que temos: Aberto, plano, fechado ou outro.
Como é que a expansão está a mudar com o tempo?
Qual o destino final do Universo?
FIM