Otimização da densidade de estados de fônons do alumínio a partir

Sociedade Brasileira de Química (SBQ)
Otimização da densidade de estados de fônons do alumínio a partir das
capacidades caloríficas a volume constante
Éderson D'M. Costa1* (PG), Nelson H. T. Lemes1 (PQ), Márcio O. Alves2 (PG), João P. Braga2 (PQ)
1
Instituto de Química, Universidade Federal de Alfenas, Alfenas-MG.
Departamento de Química, Universidade Federal de Minas Gerais, Belo Horizonte-MG.
*
[email protected]
2
Palavras chave: Fônon, Capacidade calorífica, Problema mal-colocado, Regularização de Tikhonov.
Introdução
A conexão entre a capacidade calorífica a volume
constante
, e a densidade de estados
, é
estabelecida por uma equação integral de Fredholm
de 1ª ordem,
∫
onde é a constante de Planck, a constante de
Boltzmann,
a temperatura absoluta, e
a
frequência.1 A quadratura da equação integral leva a
forma
matricial
,
que
não
pode ser resolvida de forma satisfatória por
devido a natureza mal colocada
do problema. Neste trabalho exploramos a
Regularização de Tikhonov (RT)2 que consiste em
adicionar restrições ao funcional a ser minimizado,
‖
‖
‖ ‖ , é um número positivo
que controla o peso dado à restrição e é algum
̂, em que ̂ é
operador linear, utilizou-se
uma estimativa para solução. Neste caso a solução
̂ .
é obtida por
Para a estimativa de ̂ utilizou-se a densidade de
estados obtida do trabalho de Walker,3 as
capacidades caloríficas , foram obtidas do trabalho
Giauque e Meads,4 todas essas informações, i.e. ̂
e , são informações experimentais para o alumínio.
A partir de ̂ não se reproduz
dentro do erro
experimental entre 15 a 300 K, o que está
relacionado com o erro na densidade de estados. O
erro de a 15 K é avaliado em 30%.
O parâmetro de regularização
foi
avaliado pela curva L.2 Os valores calculados de
são apresentadas na figura 2 em comparação com
os dados experimentais. Todos os valores
calculados encontram-se dentro da precisão
experimental, acima de 35 K de 0,1 a 0,2%, a 20 K
1% e a 15 K de 2 a 3%. Verificou-se também
melhoras significativas para a previsão das
propriedades termodinâmicas ,
e
, figura 3.
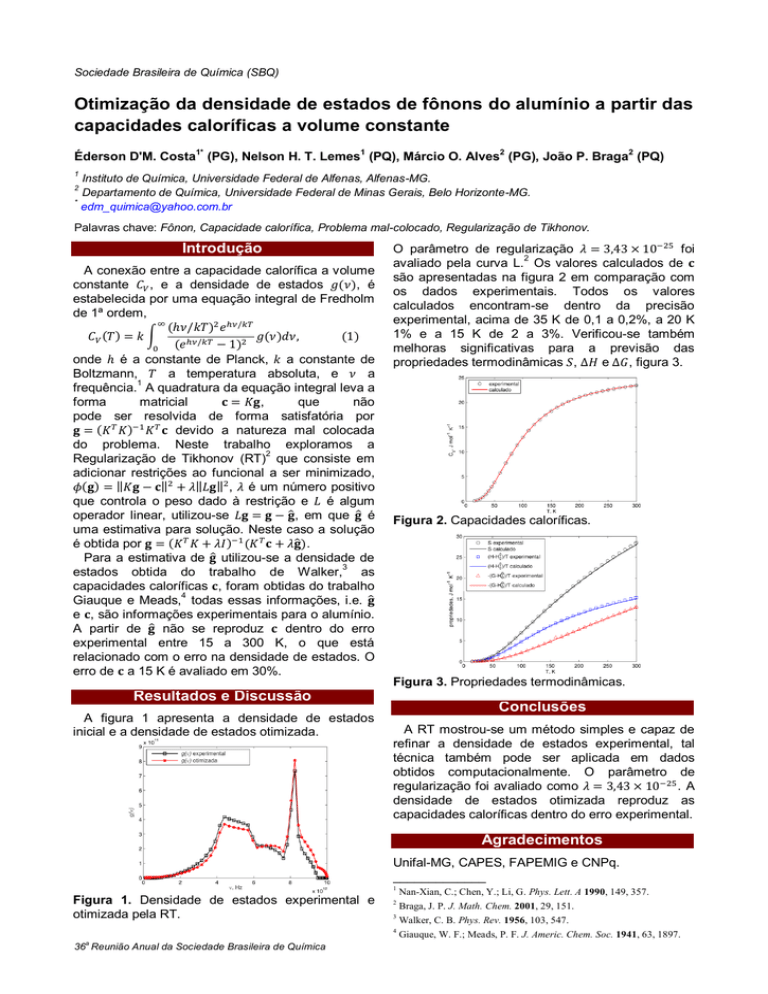
Figura 2. Capacidades caloríficas.
Figura 3. Propriedades termodinâmicas.
Resultados e Discussão
A figura 1 apresenta a densidade de estados
inicial e a densidade de estados otimizada.
Conclusões
A RT mostrou-se um método simples e capaz de
refinar a densidade de estados experimental, tal
técnica também pode ser aplicada em dados
obtidos computacionalmente. O parâmetro de
regularização foi avaliado como
.A
densidade de estados otimizada reproduz as
capacidades caloríficas dentro do erro experimental.
Agradecimentos
Unifal-MG, CAPES, FAPEMIG e CNPq.
_____________
Figura 1. Densidade de estados experimental e
otimizada pela RT.
a
36 Reunião Anual da Sociedade Brasileira de Química
1
Nan-Xian, C.; Chen, Y.; Li, G. Phys. Lett. A 1990, 149, 357.
2
Braga, J. P. J. Math. Chem. 2001, 29, 151.
3
Walker, C. B. Phys. Rev. 1956, 103, 547.
4
Giauque, W. F.; Meads, P. F. J. Americ. Chem. Soc. 1941, 63, 1897.