Conversão de Energia 01

ANOTAÇÕES DE CONVERSÃO I
1
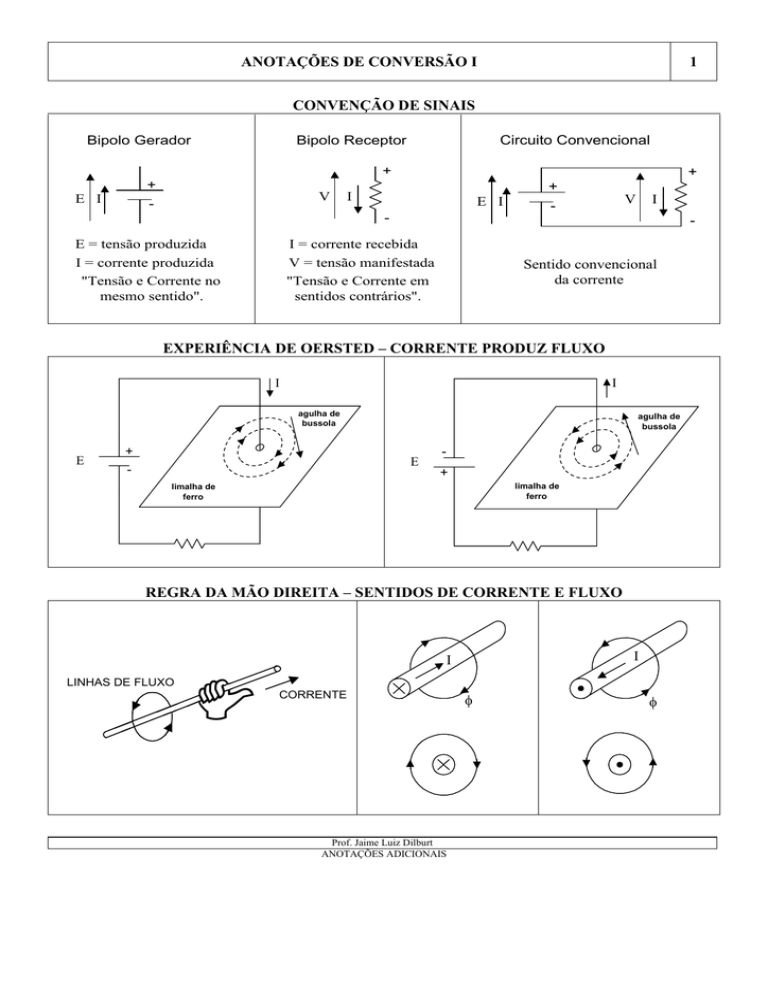
CONVENÇÃO DE SINAIS
Bipolo Gerador
Bipolo Receptor
Circuito Convencional
+
+
E I
V
-
+
I
E I
-
V
I
-
I = corrente recebida
V = tensão manifestada
"Tensão e Corrente em
sentidos contrários".
E = tensão produzida
I = corrente produzida
"Tensão e Corrente no
mesmo sentido".
+
-
Sentido convencional
da corrente
EXPERIÊNCIA DE OERSTED – CORRENTE PRODUZ FLUXO
I
I
agulha de
bussola
E
+
+
-
-
E
agulha de
bussola
limalha de
ferro
limalha de
ferro
REGRA DA MÃO DIREITA – SENTIDOS DE CORRENTE E FLUXO
I
I
LINHAS DE FLUXO
CORRENTE
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
φ
φ
ANOTAÇÕES DE CONVERSÃO I
2
PEÇAS POLARES NATURAIS (IMÃS)
LINHAS DE FLUXO
PEÇA POLAR
FACES POLARES N e S
N
S
N
S
LINHAS DE FLUXO DE PEÇAS POLARES PRÓXIMAS ENTRE SI – FACES DE
POLARIDADES OPOSTAS
N
S
S
S
N
N N
S
LINHAS DE FLUXO DE PEÇAS POLARES PRÓXIMAS ENTRE SI – FACES DE
POLARIDADES NÃO OPOSTAS. (Notar o campo magnético uniforme – linhas de fluxo paralelas
e eqüidistantes entre si)
N
S
N
S
S
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
N
S
N
ANOTAÇÕES DE CONVERSÃO I
3
FLUXO MAGNÉTICO EM UM SOLENÓIDE RETO
φ
φ
nucleo de ferro
N
S
S
N
I
I
φ
enrolamento de cobre
φ
A inversão do sentido de corrente inverte o sentido do fluxo.
Regra da Mão Direita – Enlaçando o enrolamento com a mão
direita, os dedos indicam o sentido da corrente e o polegar indica o
sentido do fluxo.
SATURAÇÃO MAGNÉTICA E HISTERESE MAGNÉTICA – CURVA DE HISTERESE
φ
φ
φ
C
B
φres.
φres.
φres.
A
I
I
PEÇA NUNCA MAGNETIZADA
PEÇA JÁ MAGNETIZADA
I
CURVA SIMPLIFICADA
LEGENDA DAS FIGURAS ACIMA
Φ → FLUXO MAGNÉTICO
Φres →MAGNETISMO RESIDUAL
Ι → CORRENTE DE EXCITAÇÃO
AB → TRECHO LINEAR
BC → TRECHO NÃO LINEAR
HISTERESE MAGNÉTICA →DIFERENÇA ENTRE AS CURVAS ASCENDENTE E DESCENDENTE
SATURAÇÃO MAGNÉTICA→ PONTO C EM DIANTE
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
ANOTAÇÕES DE CONVERSÃO I
4
GALVANÔMETRO DE ZERO CENTRAL
Instrumento habilitado para medir e indicar o sentido de corrente elétrica.
I
+
+
+
-
-
+
-
+
-
Circuito sem corrente
I
-
+
Circuitos com corrente – notar o sentido da corrente e o ponteiro do
galvanômetro
LEI DE FARADAY-LENZ → LEI DA INDUÇÃO ELETROMAGNÉTICA
FLUXO (VARIAÇÃO DE FLUXO) PRODUZ TENSÃO → e = −
φ
dφ
dt
DESCRIÇÃO
1. face polar Norte;
2. linhas de fluxo originando-se na face polar N;
3. anel condutor, em um circuito fechado por um
galvanômetro de zero central;
4. o anel vai movimentar-se de baixo para cima
ou de cima pra baixo, mantendo-se paralelo à
face polar N;
N
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
ANOTAÇÕES DE CONVERSÃO I
φinduzido resultante
φinduzido parcial
dφ
5
DESCRIÇÃO
φindutor
1. movimento do anel para baixo;
2. aumenta a quantidade de fluxo indutor enlaçada
pelo anel → dф;
3. surge uma tensão induzida entre as extremidades
do anel condutor → e = −
corrente induzida
movimento do
anel para baixo
N
φinduzido resultante
φinduzido parcial
dφ
4. surge uma corrente induzida circulando pelo
anel condutor e galvanômetro;
5. surge o fluxo induzido parcial, produzido pela
corrente circulante;
6. surge o fluxo induzido resultante, pela interação
dos fluxos induzidos parciais ao longo do anel;
restabelecendo o equilíbrio de fluxo enlaçado
originalmente pelo anel condutor.
DESCRIÇÃO
φindutor
1. movimento do anel para cima;
2. diminui a quantidade de fluxo indutor enlaçada
pelo anel → dф;
3. surge uma tensão induzida entre as extremidades
do anel condutor → e = −
corrente induzida
movimento do
anel para cima
N
dφ
;
dt
dφ
;
dt
4. surge uma corrente induzida circulando pelo
anel condutor e galvanômetro;
5. surge o fluxo induzido parcial, produzido pela
corrente circulante;
6. surge o fluxo induzido resultante, pela interação
dos fluxos induzidos parciais ao longo do anel;
restabelecendo o equilíbrio de fluxo enlaçado
originalmente pelo anel condutor.
LEI DE FARADAY-LENZ → A variação do fluxo indutor enlaçado por uma espira, provoca uma tensão
induzida, que produz uma corrente induzida, que produz um fluxo induzido cujo sentido é tal que opõe-se
à variação do fluxo indutor. (confirme esta afirmação nas 2 figuras anteriores).
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
ANOTAÇÕES DE CONVERSÃO I
6
CONDUTOR SE MOVIMENTANDO EM UM CAMPO MAGNÉTICO UNIFORME
φ
l
N
S
φ
O campo magnético uniforme se caracteriza por
apresentar linhas de fluxo paralelas e
eqüidistantes entre si, com o mesmo sentido em
qualquer posição do espaço compreendido entre
as duas faces polares paralelas.
O condutor está paralelo às faces polares, e
Vamos representar o fluxo magnético e o condutor,
perpendicular à direção do fluxo magnético
cujas extremidades tocam o trilho metálico e pode
deslizar para cima ou para baixo.
CONDUTOR EM MOVIMENTO PERPENDICULAR À DIREÇÃO DO FLUXO INDUTOR
movimento de baixo para cima
movimento de cima para baixo
l
l
2
1
secção transversal
secção transversal
corrente induzida
2
dx
φinduzido parcial
1
corrente induzida
φinduzido parcial
dx
φinduzido resultante
φinduzido resultante
dφ
dφ
φindutor
φindutor
OBS. Análise na nova área
OBS. Análise na nova área
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
ANOTAÇÕES DE CONVERSÃO I
7
CONDUTOR EM MOVIMENTO PARALELO À DIREÇÃO DO FLUXO INDUTOR
l
l
1
mov.
2
ISTO QUE FOI DESCRITO ATÉ
AGORA É TAMBÉM
CHAMADO
“EFEITO GERADOR”
φindutor
dx
Obs. – movimento de 1 para 2 ou de 2 para 1
não há alteração da área
enlaçada, não há variação de fluxo na área enlaçada, ( dφ = 0 ), logo não há
tensão induzida
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
ANOTAÇÕES DE CONVERSÃO I
8
REGRAS DA MÃO DIREITA PARA SENTIDOS DE FLUXO,
MOVIMENTO, TENSÃO E CORRENTE (efeito gerador)
Movimento
Tensão
Corrente
Fluxo
Regra de Fleming, da mão direita, do gerador.
dφ
dt
(MOVIMENTO NA DIREÇÃO PERPENDICULAR AO FLUXO MAGNÉTICO).
QUANTIFICAÇÃO DE
⎧ B = densidade de fluxo
e=−
⎫
φ ⎪
⎪
B=
⎨φ = int ensidade de fluxo ⎬ φ = BS = Blx →
S ⎪
⎩ S = área
⎪
⎭
e=−
d(Blx )
dx
= −Bl
= −Blv Volts
dt
dt
GRANDEZAS
Φ = INTENSIDADE DE FLUXO
B = DENSIDADE DE FLUXO
SISTEMA CGS
Linhas ou Maxwells
Linhas/cm2 ou Maxwells/cm2
SISTEMA MKS
Webers
Webers/m2
l = COMPRIMENTO ATIVO DO
centímetros
cm
centímetros/segundo
cm/s
e = − Blv.10 −8 Volts
metros
m
metros/segundo
m/s
CONDUTOR
v = VELOCIDADE DO CONDUTOR
(na perpendicular ao fluxo)
e = tensão induzida instantânea
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
e = − Blv Volts
ANOTAÇÕES DE CONVERSÃO I
9
TENSÃO INDUZIDA EM UM CONDUTOR EM MOVIMENTO INCLINADO COM RELAÇÃO
AO FLUXO MAGNÉTICO.
θ
v
v
v
φ
EXEMPLOS
movimento
perpendicular
ao fluxo
movimento
paralelo ao
fluxo
e = − Blv
e=0
FAÇA ESTES
movimento
inclinado
c/relação ao
fluxo: a
componente
paralela ao fluxo
não produz
tensão...
e = − Blv cos θ
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
ANOTAÇÕES DE CONVERSÃO I
10
EFEITO MOTOR
N
S
N
S
N
S
F
Condutor na presença de um campo
magnético uniforme. (vide pg. 6)
.Tensãoaplicada ao condutor,
corrente e linhas de fluxo.
Interação das linhas de fluxo e
surgimento da força F
A força que atua no condutor é dada por: F = BIl
A regra para determinar o sentido da força F é a REGRA DA MÃO ESQUERDA.
Sistema
Grandeza
MKS
CGS
MKgfS
F = BIl
F = BIl
N
Newtons
Weber/m2
Tesla
m
A
d
dinas
Maxwell/cm2
Gauss
cm
A
1 N = 105 dinas
1 Kgf = 9,81 N
BIl
9,81
Kgf
kilogramaforça
Weber/m2
Tesla
m
A
↓
F
B
l
Ι
Observações
F=
SIMULTANEIDADE DOS EFEITOS GERADOR E MOTOR – TRABALHO DE CLASSE
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
ANOTAÇÕES DE CONVERSÃO I
11
CONDUTOR EM MOVIMENTO CIRCULAR UNIFORME
EM UM CAMPO MAGNÉTICO UNIFORME
Posição referencial do condutor
Representação simplificada do movimento, em secção transversal
φ
1
2
N
1.
2.
3.
4.
5.
8
S
COMENTÁRIOS
v em cada ponto é tangencial à
trajetória;
posições 1 e 5
v é // ao fluxo:
tensão induzida nula;
posições 3 e 7
v é ⊥ ao fluxo,
tensão induzida instantânea máxima;
posições 2, 4, 6 e 8
v é inclinada
com relação ao fluxo, tensão induzida
dada por e = − Blv cos θ ;
θ = ângulo entre v e a ⊥ ao fluxo;
Sentidos das tensões obtidos com a
Regra da Mão Direita.
3
7
4
6
5
φ
FORMA DE ONDA DA TENSÃO INDUZIDA NO CONDUTOR, EM UM CICLO
ONDA SENOIDAL – TENSÃO ALTERNADA SENOIDAL
e
5
1
2
3
4
6
7
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
8
1
t
ANOTAÇÕES DE CONVERSÃO I
12
DEFINIÇÕES
1. BOBINA – área aberta plana ou não, delimitada por condutor elétrico (fio elétrico isolado).
2. ESPIRA – volta de fio. As bobinas podem ter uma ou diversas espiras, ou voltas de fio.
3. LADO ATIVO DE BOBINA – trecho reto da bobina sujeito às linhas de fluxo. (só se define para
bobinas de formas quadrada ou retangular).
4. TERMINAIS DAS BOBINAS – as 2 extremidades livres.
DIVERSAS FORMAS DE BOBINA (representação plana)
terminais
DETALHES IMPORTANTES
As espiras se superpõem, estão em contato mecânico mas não há contato elétrico entre elas. (fio isolado).
Bobina com 2 espiras
ou bobina dupla
Bobina com 3 espiras
ou bobina tripla
Lados de bobina compostos
por 1 condutor
Prof. Jaime Luiz Dilburt
ANOTAÇÕES ADICIONAIS
Lados de bobina compostos
por 2 condutores