Termodinâmica - Sou Vestibulando

© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
1
QUESTÕES CORRIGIDAS
TERMODINÂMICA
1.
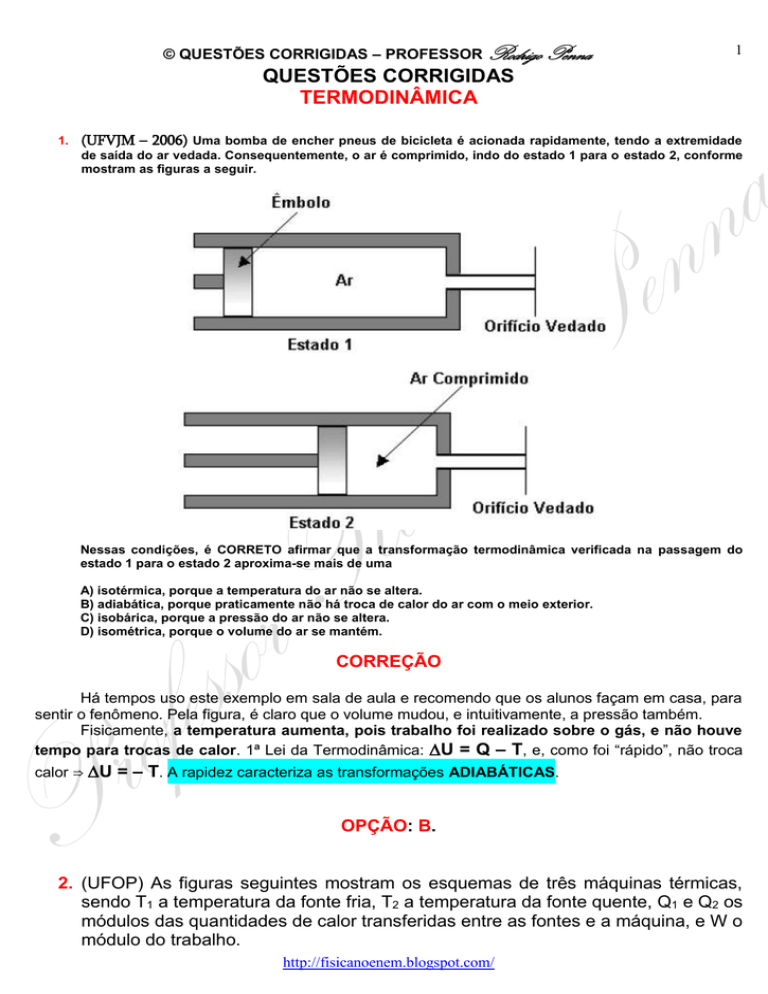
(UFVJM – 2006) Uma bomba de encher pneus de bicicleta é acionada rapidamente, tendo a extremidade
de saída do ar vedada. Consequentemente, o ar é comprimido, indo do estado 1 para o estado 2, conforme
mostram as figuras a seguir.
Nessas condições, é CORRETO afirmar que a transformação termodinâmica verificada na passagem do
estado 1 para o estado 2 aproxima-se mais de uma
A) isotérmica, porque a temperatura do ar não se altera.
B) adiabática, porque praticamente não há troca de calor do ar com o meio exterior.
C) isobárica, porque a pressão do ar não se altera.
D) isométrica, porque o volume do ar se mantém.
CORREÇÃO
Há tempos uso este exemplo em sala de aula e recomendo que os alunos façam em casa, para
sentir o fenômeno. Pela figura, é claro que o volume mudou, e intuitivamente, a pressão também.
Fisicamente, a temperatura aumenta, pois trabalho foi realizado sobre o gás, e não houve
tempo para trocas de calor. 1ª Lei da Termodinâmica: U = Q – T, e, como foi “rápido”, não troca
calor ⇒ U = – T. A rapidez caracteriza as transformações ADIABÁTICAS.
OPÇÃO: B.
2. (UFOP) As figuras seguintes mostram os esquemas de três máquinas térmicas,
sendo T1 a temperatura da fonte fria, T2 a temperatura da fonte quente, Q1 e Q2 os
módulos das quantidades de calor transferidas entre as fontes e a máquina, e W o
módulo do trabalho.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
2
Afirma-se que:
I. O esquema A representa uma máquina possível e o trabalho que ela realiza
é W = Q2 – Q1.
II. O esquema B representa uma máquina possível e o trabalho que ela realiza
é W = Q2.
III. O esquema C representa um refrigerador possível e o trabalho absorvido
por ele é W = Q2 – Q1.
Assinale a opção CORRETA:
a)
b)
c)
d)
Apenas I é verdadeira
Apenas I e II são verdadeiras.
Apenas II e III são verdadeiras.
Apenas I e III são verdadeiras.
CORREÇÃO
I – CERTO. A máquina retira calor 2, usa parte no trabalho W e rejeita o calor 1.
II – ERRADO. Nem todo o calor pode ser aproveitado como trabalho.
III – CERTO. Com a ajuda de trabalho W, o refrigerador retira calor 1 e rejeita para o
meio externo o calor 2.
OPÇÃO: D.
3. Observe no gráfico abaixo a representação do funcionamento de um dispositivo térmico.
Pressão
Volume
Observando o gráfico, RESPONDA: é uma máquina térmica ou um refrigerador?
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
CORREÇÃO
3
Trata-se de um refrigerador, pois o ciclo ocorre no sentido horário.
4. (UFMG/2006) (Constituída de dois itens.)
Pretendendo instalar um aquecedor em seu quarto, Daniel solicitou a dois engenheiros. Alberto
Pedrosa e Nilton Macieira . fazerem, cada um, um projeto de um sistema de aquecimento em
que se estabelecesse uma corrente de 10 A, quando ligado a uma rede elétrica de 220 V.
O engenheiro Pedrosa propôs a instalação de uma resistência que, ligada à rede elétrica,
aqueceria o quarto por efeito Joule.
Considere que o quarto de Daniel tem uma capacidade térmica de 1,1 x 10 5 J/oC.
1. Com base nessas informações, CALCULE o tempo mínimo necessário para que o aquecedor
projetado por Pedrosa aumente de 5,0 ºC a temperatura do quarto.
Por sua vez, o engenheiro Macieira propôs a instalação, no quarto de Daniel, de uma bomba de
calor, cujo funcionamento é semelhante ao de um aparelho de ar condicionado ligado ao
contrário. Dessa forma, o trabalho realizado pelo compressor do aparelho é utilizado para retirar
calor da parte externa e fornecer calor à parte interna do quarto.
Considere que o compressor converte em trabalho toda a energia elétrica fornecida à bomba de
calor.
Com base nessas informações,
2. RESPONDA:
O sistema proposto por Macieira aquece o quarto mais rapidamente que o sistema proposto por
Pedrosa?
JUSTIFIQUE sua resposta.
CORREÇÃO
Muito interessante! Enquanto a primeira parte aborda cálculos da eletricidade e termodinâmica,
a segunda leva o aluno a pensar, e bem!
Efeito Joule é a dissipação de calor por uma resistência percorrida por corrente. Este calor
será usado no aquecimento, que será mais fácil ou mais difícil de acordo com a Capacidade Térmica.
Energia
Vamos utilizar várias fórmulas: P = V.i, P=potência, V=”voltagem” e i=corrente; P 
;
tempo
Q
C
, C=capacidade térmica, Q=calor(energia) e t=variação de temperatura.
t
5
E
E
C.t 1,1.10 .5
2
P   V .i  t 
, masQ  C.t  t 

 2,5.10 s
t
V .i
V .i
220.10
Como toda prova de Física, e não de Matemática, os números são escolhidos a dedo!
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
Agora precisamos compreender bem a
FONTE QUENTE
Termodinâmica! O sistema proposto tem o mesmo
(QUARTO)
princípio de uma geladeira comum. Seria
equivalente a usar a parte de trás da geladeira,
aquela que muita gente utiliza para secar meias nos
dias de chuva, como aquecedor! Façamos um
Q2
esqueminha, lembrando que a geladeira é uma
Máquina Térmica funcionando ao contrário:
4
COMPRESSOR
(TRABALHO)
ζ
Calor é retirado do ambiente, pelo
Trabalho do compressor, e entregue no
Q1
quarto. Pelo esquema:
Q2 = ζ + Q1 .
Pelo enunciado, TODA a eletricidade
gasta é utilizada em Trabalho, sem perdas!
FONTE FRIA
Assim, gastando a mesma eletricidade,
(AMBIENTE
este sistema entrega ao quarto mais calor
EXTERNO)
(ζ + Q 1) do que o anterior, que entregava
somente a potência elétrica (ζ) convertida em
calor por Efeito Joule!
Muito boa a pergunta! Não me lembro de tê-la feito anteriormente. Leva o aluno a pensar, e
cobra um conhecimento Físico mais elaborado!
Com certeza, muita gente errou esta questão, ou respondeu certo, mas justificando de maneira
errada!
5. (UFVJM/2007) Tendo-se uma amostra de gás ideal em expansão isotérmica, é CORRETO
afirmar que
A) o trabalho realizado pelo gás é igual à variação de sua energia interna.
B) o trabalho realizado pelo gás é igual ao calor absorvido pelo mesmo.
C) o calor absorvido pelo gás é nulo.
D) a energia cinética média das moléculas do gás aumenta.
CORREÇÃO
Tratando dos Gases e da 1a Lei da Termodinâmica, mas como não trouxe desenho fica
totalmente teórica e meio sem graça. Vamos à lei:
U = Q – τ, onde U é a variação da energia interna (ligada à temperatura absoluta)(J, cal), Q o
calor (trocado entre o gás e o meio a sua volta) (J, cal) e
volume) (J, cal).
τ o Trabalho (ligado à variação de
Para uma transformação Isotérmica  Tfinal = Tinicial  U = UF - Ui ≈ TF - Ti = 0. Então:
0=Q–τ
 τ = Q . O trabalho realizado é igual ao calor recebido.
OPÇÃO: B.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
5
6. Uma certa amostra gasosa recebe 500 cal de calor trocado com o meio
externo e realiza um trabalho igual a 200 cal. A variação de sua energia
interna será igual a:
a)
b)
c)
d)
300 cal.
700 cal.
2,5 cal.
0,4 cal.
CORREÇÃO
1ª Lei da Termodinâmica: U = Q –   U = 500 – 200 = 300 cal.
OPÇÃO: A.
7. A figura abaixo representa um esquema de uma geladeira.
Site http://netfisicaonline.com/geladeira.html em 01/06/2008.
Marque entre as opções abaixo aquela que representa corretamente o funcionamento
da geladeira.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
6
a) No interior da geladeira, o motor elétrico retira calor dos alimentos e o gás que
circula bombeia o calor para fora.
b) A geladeira é uma máquina térmica funcionando ao contrário, retirando calor da
fonte fria através da realização de trabalho externo do motor e liberando calor
para fonte quente, o ambiente externo.
c) O calor dos alimentos flui através do gás e o motor obriga o calor recolhido a
expandir-se, liberando-o na parte traseira.
d) O calor passa naturalmente dos alimentos para um gás apropriado, capaz de
atraí-lo, e o mesmo gás, pela ação do motor, repele o calor para o lado de fora da
geladeira.
CORREÇÃO
De fato, a geladeira é uma máquina térmica ao contrário, como diz a letra B. As outras
opções não têm nenhum fundamento físico.
OPÇÃO: B.
8. Explique a convenção de sinais quando calculamos o trabalho realizado por um
gás ou sobre um gás.
CORREÇÃO
O trabalho realizado pelo gás durante a expansão é positivo e realizado sobre o gás
durante a compressão é negativo.
9. (UFOP/1o 2008) Considerando-se um gás ideal, assinale a alternativa incorreta.
A) O trabalho realizado em uma transformação isovolumétrica é nulo.
B) O calor específico molar sob pressão constante é maior que o calor específico molar a volume
constante.
C) Em uma transformação adiabática, o calor trocado entre um sistema e sua vizinhança é nulo.
D) Em um processo sob pressão constante, o produto da pressão P pelo volume V se mantém
constante.
CORREÇÃO
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
7
Gases e Termodinâmica.
a) CERTA. Um gás só realiza trabalho quando seu volume varia. Aliás, o Trabalho de um gás
é dado pela área do gráfico Pressão versus Volume. Veja.
P (Pa)
P (Pa)

V (m3)
V (m3)
Observe que, à esquerda, numa transformação Isobárica, a área é a do retângulo, que dá o
Trabalho . À direita, na Isovolumétrica (ou Isocórica) não existe área sob a reta.
b) CERTA. Não gosto sequer de comentar estes conceitos em sala no Ensino Médio, por absoluta
falta de necessidade! Calor específico molar é o mesmo que Calor Específico, grandeza que
mede a facilidade ou dificuldade de se esquentar ou se esfriar uma substância. Quanto maior o
calor específico, mais difícil de se esquentar: quer dizer, tem que se gastar mais calor para se
esquentá-la. A diferença do molar é que ele é válido para um mol de gás, só isso. Agora,
ilustremos o caso Isobárico e o Isovulumétrico.
A figura á esquerda foi retirada da prova da
UFMG/2002. Ela mostra um gás preso com
êmbolo móvel, mantendo a Pressão constante.
A figura da direita, tirada do images.google
mostra um aerosol. Se você não apertar a válvula,
lá dentro o gás mantém seu Volume constante.
Conforme comentado o ítem anterior, numa
transformação Isobárica, o gás pode realizar
trabalho, e na isovolumétrica não. Vejamos a
Primeira lei da Termodinâmica.
U  Q 
Ela nos informa que a variação da energia interna U depende do calor Q trocado e do Trabalho 
realizado. Na isovolumétrica, como o gás não pode realizar trabalho, ao receber calor esquenta
mais – todo calor Q é transformado em aquecimento U. Portanto, o calor específico é menor.
Na isobárica, parte do calor é usada para trabalho – erguer o êmbolo – e, nesse caso, o gás
esquente menos, tendo o calor específico maior, pois é mais difícil de esquentar. Só parte do calor
Q é transformada em aquecimento U, pois há o “– trabalho ”.
c) CERTA. É justamente a definição de Transformação Adiabática: é tão rápida que não dá
tempo de trocar calor.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
d) ERRADA! O primeiro gráfico acima mostra isto. Mas, usando Clapeyron:
pressão é constante, teríamos:
8
PV PV
 o o . Como a
T
To
PV Po Vo

. Vemos que é a razão entre o volume e a
T
To
temperatura (Kelvin) que se mantém constante, ou V  T .
OPÇÃO: D.
10. (UFMG/2009) Para estudar o comportamento de um gás, um professor montou o sistema
representado nesta figura:
Nesse sistema, um recipiente de volume V, dotado de um êmbolo e de um registro R, contém um
gás que se comporta como um gás ideal. Um manômetro, que consiste em um tubo de vidro, em
forma de U, que contém mercúrio, tem uma de suas extremidades conectada ao recipiente, por
intermédio do registro R, e a outra extremidade aberta.
Inicialmente, o registro está aberto e o gás está à pressão atmosférica p0 e à temperatura
ambiente T0.
Sejam d a densidade do mercúrio e he e hd a altura das colunas de mercúrio, nos ramos da
esquerda e da direita do tubo, respectivamente.
1. A partir de certo instante, o professor comprime o êmbolo, lentamente, para que o gás se
mantenha à temperatura ambiente, até reduzir à metade o volume ocupado, no recipiente, pelo
gás.
Considerando essa situação, DETERMINE a diferença de altura (he - hd) entre as duas colunas de
mercúrio no tubo de vidro, em termos de p0, d e g.
2. Em seguida, o professor fecha o registro R e puxa o êmbolo, rapidamente, até este retornar à
posição inicial.
Isso feito, ele abre o registro R e, ao mesmo tempo, observa o nível de cada uma das colunas de
mercúrio no tubo de vidro.
Considerando essa nova situação, RESPONDA:
A altura he é menor, igual ou maior que a altura hd?
JUSTIFIQUE sua resposta.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
9
CORREÇÃO
A TERMODINÂMICA, enfocando o Comportamento dos Gases, que a UFMG tanto aborda.
Logo, nenhuma surpresa.
No item 1 temos uma Transformação Gasosa. Fácil de identificar, por sinal. Segundo o texto
da questão, “o professor comprime o êmbolo, lentamente, para que o gás se mantenha à temperatura
ambiente”. Manter-se na mesma temperatura, ambiente, em que estava implica numa Transformação
Isotérmica, na qual a temperatura permanece constante – como eu costuma tratar, = k). Logo, outras
duas variáveis de estado do gás se alteram: o volume, a que a questão se refere, e a pressão, que
irá provocar a diferença de altura.
No enunciado, temos que o volume se reduz à metade. Fiz uma figura para ilustrar.
Patm
he – hd = h
Veja que pressionar o gás fez a coluna de mercúrio se deslocar para a esquerda em relação ao
nível de equilíbrio original, que deixei marcado. Podemos utilizar a Equação de Clapeyron que trata
do comportamento dos gases, a famosa “puta veia”... PV=nRT .
E, importante citar na resolução: como o gás está confinado, preso, o número de moles n
permanece constante. Então:
PV PV
 o o
T
To
. O produto pressãoxvolume / temperatura
permanece constante! Substituindo os dados, genéricos, fornecidos, calculamos a pressão atingida
pelo gás:
P
Vo
2  po Vo  P  p  P  2 p
o
o
2
To
To
. O que era esperado por um aluno que
compreende bem as transformações: se o volume se reduz pela metade, a pressão dobra!
Porém, a questão quer a diferença de altura! Marquei na figura, veja acima. Observe que o
gás sustenta a pressão atmosférica (Po) mais a diferença de altura he – hd da coluna de mercúrio!
Stevin nos ensina a calcular a pressão de um fluido numa profundidade qualquer:
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
10
P  Po  dhg
. O termo dhg é a chamada pressão hidrostática, devida à diferença de
altura, neste caso, das colunas de mercúrio! E a pressão inicial po é a atmosférica. Claro, a altura h,
então, é he – hd.
Podemos usar o Teorema de Stevin e calcular a altura h diretamente na fórmula acima.
Vamos lá...
2 po  po  dhg  2 po  po  dhg 
po
po
po  dhg  h 
 he  hd 
dg
dg
.
Apesar da aparência, não é tão complicado quanto se parece.
Quanto ao item 2, carece um cuidado maior. Pensando no contrário da transformação anterior,
se o professor puxasse o êmbolo lentamente, mantendo o registro aberto e a temperatura constante,
tudo voltaria ao início, com os mesmos valores de pressão, volume e temperatura. Mas, não foi o que
ele fez...
Para começar, a próxima transformação ocorreu, segundo a questão, “rapidamente”, o que
caracteriza uma mudança Adiabática. Tão rápida que não dá tempo de trocar calor com o ambiente.
U  Q 
Da 1a Lei da Termodinâmica, temos:
. Aqui, U é a variação da energia interna,
ligada à temperatura, o estado de agitação das partículas que compõem o gás; Q é o calor trocado,
U  0   
no caso zero;  é o trabalho realizado pelo gás. Então:
. Vemos que a
variação da energia, ou seja, a temperatura do gás depende do trabalho realizado pelo gás.
Caso se queira relacionar a Energia Interna com a Temperatura não com argumentos teóricos
mas com a Teoria Cinética dos Gases tem-se: U 
3
nRT
2
.
Como o gás se expande, ele realiza um trabalho positivo. Na prática, quer dizer que quando
o professor puxa o êmbolo dando-lhe mais espaço ele gasta sua própria energia interna para
aumentar de volume e ocupá-lo. Logo, sua temperatura, fator importante, diminui em relação à
temperatura ambiente, que manteve até então.
PV
 constante , permanece
Como ele continua confinado e não vazou, a relação anterior,
T
valendo. Já que o volume volta a ser V e concluímos que a temperatura diminui em relação à
inicial, a pressão não pode ser a mesma que a inicial! A relação mostra que a pressão deve
diminuir para compensar a diminuição da temperatura:
P  V (o mesmo)
 constante
T
!
Chegando ao final dos argumentos, como a pressão final do gás vai ser menor do que a que
ele tinha antes e antes era a atmosférica, o gás fica com pressão menor que a atmosférica!
http://fisicanoenem.blogspot.com/
11
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
Portanto, assim que o professor abrir o registro, sendo a pressão atmosférica maior, ela irá deslocar a
coluna de mercúrio agora para a direita. Fiz novamente uma ilustração do caso.
Assim, agora teremos he < hd . E foi mais complicado argumentar porque do que fazer a conta
do item 1!
11.
(PUC-RS/2005) A temperatura de um gás é diretamente proporcional à
energia cinética das suas partículas. Portanto, dois gases A e B, na mesma
temperatura, cujas partículas tenham massas na proporção de mA/mB = 4/1, terão
as energias cinéticas médias das suas partículas na proporção EcA/EcB igual a
a) 1/4
b) 1/2
c) 1
d) 4
CORREÇÃO
Problema interessante sobre a Teoria Cinética dos Gases. A questão fala sobre
a proporcionalidade, e a equação completa envolve a constante de Boltzmann:
EC 
3
KT , ou EC  T
2
. E aí a questão simplifica para os atentos: mesma
temperatura  mesma Energia Cinética. Só isto... Independente da massa!
Agora, algo que a questão não pergunta é o seguinte: tendo a mesma energia
cinética e a massa de A sendo 4 vezes maior, e quanto à velocidade das partículas do
gás A? Mas, é outra pergunta...
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
Aproveitando:
m.v 2
EC 
2
12
. Para ter a mesma cinética, as moléculas de A
4 m.(
devem ter ½ da velocidade de B. Veja porque: EC 
2
v 2
)
2
.
OPÇÃO: C.
12.
(UFMG/94) Como conseqüência da compressão adiabática sofrida por um
gás, pode-se afirmar que
a) a densidade do gás aumenta, e sua temperatura diminui.
b) a densidade do gás e sua temperatura diminuem.
c) a densidade do gás aumenta, e sua temperatura permanece constante.
d) a densidade do gás e sua temperatura aumentam.
CORREÇÃO
Aplicação da 1ª Lei da Termodinâmica, U = Q – , e conhecimento sobre o
significado de Adibática. Significa que ocorre tão rápido que não dá tempo de trocar
calor. Sendo assim, Q = 0 e
U = – .
Sem
tantas
preocupações com sinais,
pense em termos de energia.
Ao comprimir um gás, quem
gasta energia é você. Como
a energia se conserva, ele
deve ir para algum lugar, no
caso, o próprio gás! Sua
temperatura aumenta. Agora,
no decoreba, ao comprimir o
trabalho é negativo. Menos
com menos da fórmula dá
mais,
U
–
ligado
à
temperatura – vai aumentar. Veja o esqueminha com a compressão.
Além disto, por ocupar menos volume, a densidade do gás aumenta.
OPÇÃO: D.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
13
13.
(PUC-Camp/97) O esquema a seguir representa trocas de calor e realização
de trabalho em uma máquina térmica. Os valores de T1 e Q1 não foram indicados
mas deverão ser calculados durante a solução desta questão.
Considerando os dados indicados no esquema, se essa máquina operasse segundo um
ciclo de Carnot, a temperatura T1, da fonte quente, seria, em Kelvins, igual a
a)
b)
c)
d)
375
400
1200
1500
CORREÇÃO
Esquema tradicional da Máquina Térmica, utilizando o Calor Q1 da fonte quente para
 e rejeitando calor Q2 para a chamada fonte fria. Fácil calcular o
calor rejeitado: retirou 4.000, aproveitou 800, sobram 3.200 J de energia ( Q2 + = Q1 ).
realizar Trabalho
Quanto ao rendimento, refere-se à parte do calor aproveitado:
http://fisicanoenem.blogspot.com/
r
r
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna

Q1
, mas   Q1  Q2  r 
14
Q1  Q2

Q1
Q1 Q2
Q

 r  1 2
Q1 Q1
Q1
.
Porém, operando no Ciclo de Carnot, ele mostrou que o rendimento máximo será:
r  1
T2
T1
. Brincando de matemática básica:
4
75
Q2 T2
3200 300
 

 T1  375 K
Q1 T1
T1
4000
.
5
OPÇÃO: A.
14.
Quando pressionamos um aerossol e o gás sai, sentimos um abaixamento
na temperatura do frasco. Veja a figura. Este resfriamento é
explicado pelas leis da Termodinâmica. Escolha entre as opções
abaixo aquela que representa a melhor explicação para este
fenômeno.
a) O gás está sofrendo uma expansão rápida, ou seja, adiabática.
Ao realizar trabalho para se expandir, ele gasta sua energia interna e isto se
manifesta no abaixamento de sua temperatura.
b) A abertura da válvula do aerossol permite a troca de calor com o ambiente. Calor
do gás sai pela válvula, reduzindo sua temperatura.
c) Ao apertarmos a válvula realizamos trabalho sobre o gás. De acordo com a 1ª Lei
da Termodinâmica, este trabalho que realizamos tem o sinal positivo, que devido
ao sinal negativo da equação, se traduz em um abaixamento de temperatura.
d) A temperatura de um gás está relacionada ao número de moléculas que sua
amostra possui. Abrindo a válvula e perdendo moléculas, o gás perde também
temperatura.
CORREÇÃO
A saída do gás é rápida: adiabática. Sua expansão, para sair, se dá às custas de sua
própria energia interna, que se reduz. E esta está ligada à temperatura, que abaixa.
OPÇÃO: A.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
15. (UFVJM/2009) Analise estas afirmações.
15
I. Um gás perfeito sofre uma transformação adiabática se, e somente se, for colocado em
um recipiente de volume variável com paredes revestidas por material isolante térmico.
II. Um gás perfeito, ao ganhar calor da vizinhança, apresenta um aumento em sua energia
interna, que independe do trabalho realizado.
III. Um gás perfeito, ao sofrer uma transformação cíclica, apresenta trabalho igual ao calor.
Com base nessa análise, ASSINALE a alternativa que contém apenas afirmação correta.
A) I e II
B) II e III
C) I
D) III
CORREÇÃO
Cada item...
I.
Errado. Adiabático significa tão rápido que não dá tempo de trocar calor.
Lembre-se de que não há isolantes perfeitos.
II.
Errado. Temos a 1ª Lei da Termodinâmica, conhecimento fundamental: U = Q
III.
-  . A energia interna varia, sempre, dependendo do calor e do trabalho.
CERTO. Veja um ciclo: o gás vai e volta ao ponto A, na mesma temperatura,
logo U = 0 e Q = .
Pressão
Volume
OPÇÃO: D.
16. (UNIMONTES/2009) Uma máquina térmica ideal, operando sob o ciclo de Carnot, converte uma
quantidade de energia igual a 800 J em trabalho útil, por ciclo. A máquina trabalha com fontes
térmicas a 400 K e 500 K, denominadas fonte fria e fonte quente, respectivamente. Determine a
quantidade de calor rejeitado à fonte fria.
A) 4000 J.
B) 1600 J.
C) 800 J.
D) 3200 J.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
16
CORREÇÃO
Q2
T2
r

1


1

Como Carnot demonstrou, o rendimento é dado por :
Q1
T1 . Então:
r  1
4 00 1
  20% . A outra conta é de cabeça... Se rendendo 20% a máquina
5 00 5
aproveita 800 J, então está recebendo 4.000 J de calor!
E, finalmente, destes 4.000, desperdiça 3.200 J de calor!
OPÇÃO: D.
17. (UFV/2009) Em um certo processo termodinâmico, o sistema não troca calor com a sua
vizinhança. E CORRETO inferir que, nesse processo, necessariamente:
a) a pressão no sistema aumenta.
b) a temperatura do sistema e constante.
c) o trabalho realizado pelo sistema e igual ao produto da sua pressão inicial pela variação de volume.
d) o módulo da variação da energia interna do sistema e igual ao módulo do trabalho realizado por ele.
CORREÇÃO
Temos a 1ª Lei da Termodinâmica, conhecimento fundamental: U = Q (não troca calor), teremos U = -  ou
.
 . Se Q = 0
U  
OPÇÃO: D.
18. (UNIMONTES/2009) Uma amostra de um gás perfeito passa do estado A para o estado B, sob
pressão constante de 80
N/m2, absorvendo 2 × 103
Joules de calor. O volume V
e
a temperatura T dessa
amostra estão representados
no
gráfico.
Calcule
o
aumento da energia interna,
durante a transformação.
A) 200 J.
B) 500 J.
C) 300 J.
D) 400 J.
CORREÇÃO
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
Sob pressão constante, isobárica, vale:
17
 =P. V . Do gráfico, o volume vai de 10 para
30 m3, variando 20... Logo:  = 80.20 = 1.600 J.
Da 1ª Lei da Termodinâmica, U = Q -  , temos U = 2000 – 1600 = 400 J.
OPÇÃO: D.
19.
Durante incêndios, uma grande preocupação dos bombeiros é com os
botijões de gás, como os ilustrados ao lado. Recebendo uma
quantidade calor para a qual não estão preparados, a conseqüência
conhecida é que eles podem simplesmente explodir. E, neste caso,
são capazes de grandes estragos. Veja a próxima figura que mostra,
exatamente, o que pode ocorrer em um acidente como este! Dentro
dos botijões, o gás de cozinha – GLP – pode ter seu comportamento
descrito como um chamado Gás Ideal, aproximadamente. Escolha entre as
opções abaixo aquela que descreve corretamente o tipo de
transformação gasosa a que o gás, no interior do botijão,
estará sujeito. Transformação esta que leva o botijão a explodir.
a) Isotérmica.
b) Isobárica.
c) Isovolumétrica.
d) Adiabática.
CORREÇÃO
Questão bem simples. Basta lembrar que, antes de explodir, embora o botijão até dilate,
mas pouco, podemos considerar seu volume como praticamente constante. E,
devido a isto, ao receber calor, a temperatura e a pressão aumentam até o ponto em
que ele não suporta mais.
OPÇÃO: C.
20.
U = Q - .
Escreva a 1ª Lei da Termodinâmica.
CORREÇÃO
21.
Cite o tipo de transformação gasosa que ocorre tão rápida que não dá
tempo de trocar calor.
CORREÇÃO
Adiabática.
22.
Um gás sofre uma transformação gasosa como a mostrada no diagrama
Pressão x Volume a seguir, passando de um estado inicial i para um final f.
a) Diga o tipo de transformação sofrida pelo gás.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
18
b) Responda: sua temperatura aumenta, diminui ou não se altera?
P (Pa)
f
i
V (m3)
CORREÇÃO
Como o volume não se altera, é uma transformação isovolumétrica. Além disto,
observando que a pressão aumenta, então a temperatura também aumenta. Fica
como tarefa justificar, pela 1ª Lei da Termodinâmica, por que o gás está recebendo
calor e também verificar, pelas isotermas do gráfico – não traçadas – que a temperatura
visivelmente aumenta.
23. (UEMG/2009) Um gás é aquecido no interior de um recipiente dotado de êmbolo móvel, de tal
maneira que o trabalho realizado pelo gás é igual ao calor que ele recebe, conforme ilustração a
seguir:
Assinale a alternativa que mostra CORRETAMENTE o que aconteceu, durante o processo,
nas condições descritas acima:
A) A temperatura do gás permaneceu constante.
B) A pressão do gás permaneceu constante.
C) A temperatura do gás aumentou, pois ele é aquecido.
D) A pressão e a temperatura do gás permaneceram constantes.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
19
CORREÇÃO
1ª Lei da Termodinâmica: U = Q -  . Do enunciado, temos que o calor é igual ao
trabalho! Portanto: U = Q – Q = 0, o que significa que a temperatura não varia.
OPÇÃO: A.
24.
O esquema abaixo representa o funcionamento de uma máquina térmica.
EXPLIQUE-O de forma fisicamente correta e objetiva.
CORREÇÃO
Uma máquina térmica retira calor da chamada fonte quente (Q2) à temperatura T2
, utiliza parte para realizar trabalho W (alguma aplicação tecnológica) e rejeita para
fonte fria à temperatura T1 uma quantidade de calor Q1 (desperdício).
Notar que os índices 1 e 2 estão trocados em relação à maioria dos livros, mas o
esquema é literalmente idêntico.
25. (UFMG/2010) Uma máquina térmica é
constituída de um cilindro, cheio de
gás, que tem um êmbolo móvel.
Durante o funcionamento dessa
máquina, o gás é submetido a um
processo cíclico, que o leva de um
estado K a outro estado L e, depois,
de volta ao estado K e assim
sucessivamente, como representado
no diagrama pressão versus volume,
mostrado na figura ao lado.
Considerando
essas
informações,
ESPONDA:
A) Em qual dos dois estados – K ou L – a
temperatura do gás é maior?
JUSTIFIQUE sua resposta.
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
20
B) Em um ciclo completo, em que o gás sai do estado K e volta ao mesmo estado, essa máquina realiza
trabalho líquido?
JUSTIFIQUE sua resposta.
C) Tendo-se em vista que se trata de um sistema ideal, é possível converter em trabalho todo o calor
fornecido a essa máquina?
JUSTIFIQUE sua resposta.
CORREÇÃO
A Termodinâmica. Envolve conhecimento, mas não achei esta tão complicada.
Quanto ao item A, em qual estado (K ou L) a temperatura é maior, podemos justificar de dois
modos bem distintos. Escrevendo a famosa equação de Clapeyron, a “puta velha”...
PV  nRT
. Dela, vemos que, se o número de mols n permanecer constante, o que
ocorre quando o gás (neste caso considerado idel) está preso (confianado) na máquina, dentro de
um cilindro com êmbolo, e sendo R já é uma constante, então a Temperatura é proporcional ao
produto Pressão x Volume (T  P.V). No gráfico, observamos que para L os valores da Pressão e
do Volume são maiores do que em K. Veja...
TK
TL > TK
VK
VL > VK
PL > PK
PK
No gráfico, como disse, em L os valores de P e V são maiores. Logo, em L a temperatura é
maior. Outra maneira pela qual gosto de visualizar é através das Isotermas, hipérboles, curvas que
neste caso mostram pontos de temperaturas constantes.
Note que a isoterma de K é mais baixa que a de L, logo sua temperatura é menor.
Quanto ao item B, vou argumentar pela área sob o
gráfico, conhecimento fundamental. Ela fornece o trabalho.
Durante a expansão, o gás realiza trabalho (positivo), e
durante a compressão trabalho é realizado sobre ele
(negativo). O chamado Trabalho Líquido é a diferença entre
estes dois, e é dado pela área dentro do círculo. Como se vê,
trabalho positivo é maior que o negativo e há portanto, sim,
trabalho líquido. O que significa que a máquina realmente
cumpriu seu papel: como num carro, por exemplo, moveu as
rodas.
http://fisicanoenem.blogspot.com/
o
21
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
Finalmente, em C, um dos enunciados da famosa e filosófica 2a Lei da Termodinâmica, diz que não
existe máquina térmica cujo rendimento seja de 100%. O que quer dizer que não é possível
converter em trabalho todo o calor...
26. (UFMG/2011) Um pistão - constituído de um cilindro e de um êmbolo, que
pode se mover livremente – contém um gás ideal, como representado na
Figura I. O êmbolo tem massa de 20 kg e área de 0,20 m 2. Nessa
situação, o gás está à temperatura ambiente e ocupa um volume VI.
Considere quaisquer atritos desprezíveis e que a pressão atmosférica é de 101
kPa.
1. Com base nessas informações, DETERMINE a pressão do gás dentro do
pistão.
2. Em seguida, o pistão é virado de cabeça para baixo, como mostrado na
Figura II. Nessa nova situação, a temperatura continua igual à do
ambiente e o volume ocupado pelo gás é VII.
Com base nessas informações, DETERMINE a razão VII / VI entre os
volumes.
3. Assinalando com um X a quadrícula apropriada, RESPONDA:
Ao passar da situação representada na Figura I para a mostrada na Figura II,
o gás dentro do
cilindro cede calor, recebe calor ou não troca calor?
Cede calor.
Recebe calor.
Não troca calor.
JUSTIFIQUE sua resposta.
CORREÇÃO
Questão de Termodinâmica, envolvendo Gases. Pistões com gases não são novidade: além
de fazerem parte dos motores à combustão, povoam a muito as provas da UFMG. Como se vê tanto
na 1ª quanto na 2ª etapas.
O item 1 envolve o Equilíbrio, e a 1ª Lei de Newton (Fres=0), por
sinal já cobrada nesta prova. Veja as forças que atuam e equilibram o pistão
na figura I.
A Força do Gás, para cima, precisa equilibrar o Peso do Êmbolo e
também a Força devido à Pressão Atmosférica, ou seja, devido ao peso
da camada de ar da atmosfera. Talvez haja alguma confusão entre Pressão
e Força por parte de alguns. Escrevendo o Equilíbrio.
f gás
f Patm
Pêmbolo
Fgás  Pêmbolo  FPatm
Agora, lembramos o conceito de Pressão: a força distribuída em uma área:
força F
P
  F  P. A . O Peso é uma força, igual ao produto “m.g”, mas os dados da questão
área
A
http://fisicanoenem.blogspot.com/
22
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
trazem Pressão. No caso do gás e da força devido à pressão atmosférica, temos que substituir.
Assim:
Pgás A  m. g  Patm A .
Temos dados, unidades corretas, fazer as contas...
Pgás .0, 20  20.10  101.103.0, 20 
2
2
2
Pgás .  200  101.10 3 .

10
10
2
Pgás .  200  20200 
10
10200
2
Pgás .  20400  Pgás  102000 
10
Pgás  102.103  102 kPa
Como esperávamos, o gás tem pressão maior que a atmosférica, tanto que sustenta a mesma e
o êmbolo.
O item 2 é interessante. Ao virar o pistão de ponta a cabeça, a pressão atmosférica continua
sustentando um peso de 20 kg, do êmbolo. Ela é grande!
Neste vídeo, no meu blog, mostro como ela esmaga facilmente um tambor. Olhe lá:
- http://quantizado.blogspot.com/2009/06/pressao-atmosferica.html .
Temos que observar a configuração de forças na nova situação, para o novo Equilíbrio.
Observe que o Peso do êmbolo continua para baixo. Porém, o gás
agora pressiona o êmbolo para baixo. E, como o pistão é aberto embaixo, a
Patm
pressão atmosférica empurra para cima. Muitas pessoas simplesmente não
enxergam a pressão atmosférica atuando para cima. Há uma famosa
experiência de se emborcar um copo cheio d’água, para mostrar isto. Quer
ver?
f gás
http://www.youtube.com/watch?v=hq3FszCVbFE&feature=related .
êmbolo
f
P
Novamente, temos os dados, restam as contas...
Fgás  Pêmbolo  FPatm  Pgás A  m. g  Patm A 
Pgás .0, 20  20.10  101.103.0, 20 
2
2
2
Pgás .  200  101.10 3 .

10
10
10000
2
Pgás .  20200  200  20000 
10
Pgás  100000  100.103  100 kPa
http://fisicanoenem.blogspot.com/
© QUESTÕES CORRIGIDAS – PROFESSOR Rodrigo Penna
23
Sabemos a pressão na situação II, e não terminamos. A pressão diminuiu, e a pergunta é sobre
a razão entre os volumes final e inicial. Só de virar de cabeça para baixo, creio intuitivamente a
pessoa imagina o volume crescendo. Se não, as fórmulas e contas mostrarão. Da equação dos gases
ideais, Clapeyron, a famosa “puta veia não rejeita tarado”, temos: PV=nRT. Se o gás está preso, o
número de “mols”, n, permanece constante. Leva à tradicional proporcionalidade nas transformações
gasosas. No caso, o enunciado diz: temperatura constante!
PII .VII PI .VI
V
P

 II  I 
VI PII
TII
TI
VII 102

 1,02
VI 100
Olhando o resultado, como a pressão ficou inversamente proporcional ao volume, se este
cresceu a pressão diminuiu. Foi o que ocorreu.
A última pergunta é sobre troca de calor Q, e envolve a 1ª Lei da Termodinâmica. Matéria que
exige grande clareza por parte do aluno. E correção sobre a convenção de sinais, na Física.
U = Q - , onde:
- U é a variação da energia interna de um gás, vinculada à temperatura (grau de agitação das
partículas que compõem este gás). É positiva quando a temperatura e energia interna aumentam, e
vice-versa;
- Q é o calor trocado pelo gás com o ambiente (vizinhança). É positivo quando o gás ganha calor, e
vice-versa;
-  é o trabalho, mais chato e menos compreendido pelos estudantes. Trabalho não deixa de ser uma
troca de energia. Quando um gás é “espremido”, você dá energia a ele. Ao contrário, quando ele se
expande, gasta sua energia interna para “aumentar de tamanho”. O trabalho é positivo quando o gás
se expande e negativo quando ele é comprimido.
Já ilustrei um motor a combustão, nesta prova, ali atrás. Sem clareza sobre o modelo cinético
de
um
gás
o
aluno
se
complica.
Eis
uma
explicação
on
line:
http://www.youtube.com/watch?v=EtKKpRzB-y0 .
Como a temperatura não muda, temos U = 0  0 = Q - 
  = Q.
A razão entre os volumes, 1,02, nos mostrou que o gás expandiu um pouco, isto é, seu
volume aumentou: VII > VI  VII / VI > 1. Nesta expansão, ele realizou trabalho (para “aumentar de
tamanho”) positivo. Logo, ganhou calor (positivo, + = +) ao longo desta expansão, para poder se
expandir sem esfriar, mantendo a temperatura constante.
Recebe calor.
http://fisicanoenem.blogspot.com/