ramiltonfisica.blogspot.com LISTA 2 – 1

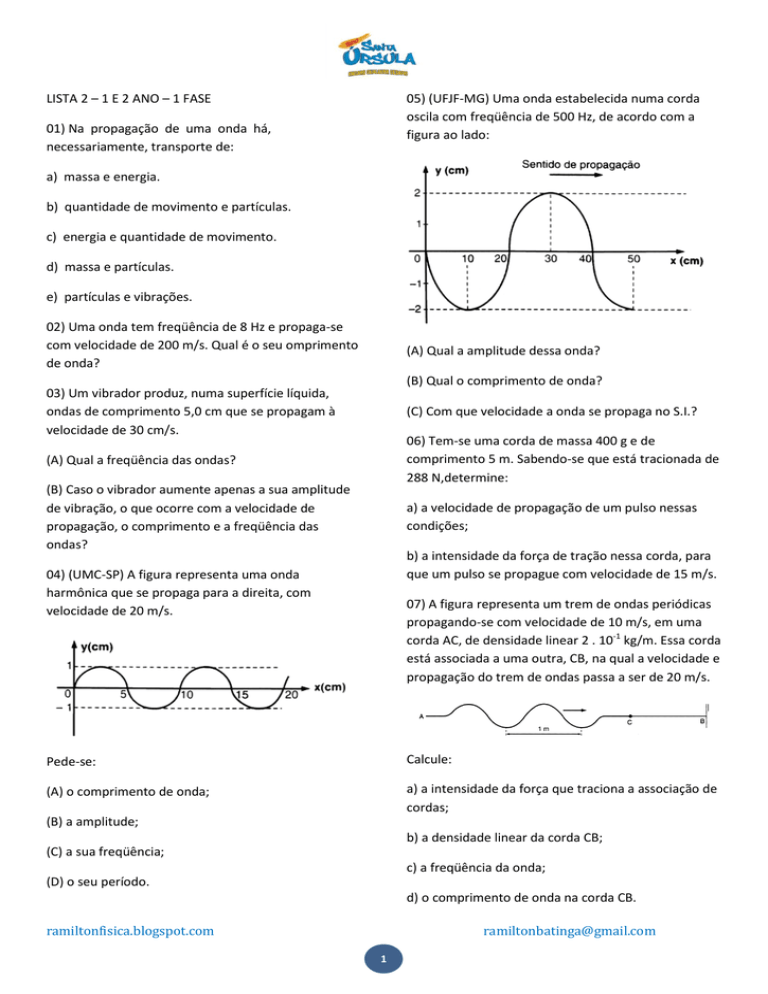
05) (UFJF-MG) Uma onda estabelecida numa corda
oscila com freqüência de 500 Hz, de acordo com a
figura ao lado:
LISTA 2 – 1 E 2 ANO – 1 FASE
01) Na propagação de uma onda há,
necessariamente, transporte de:
a) massa e energia.
b) quantidade de movimento e partículas.
c) energia e quantidade de movimento.
d) massa e partículas.
e) partículas e vibrações.
02) Uma onda tem freqüência de 8 Hz e propaga-se
com velocidade de 200 m/s. Qual é o seu omprimento
de onda?
(A) Qual a amplitude dessa onda?
(B) Qual o comprimento de onda?
03) Um vibrador produz, numa superfície líquida,
ondas de comprimento 5,0 cm que se propagam à
velocidade de 30 cm/s.
(C) Com que velocidade a onda se propaga no S.I.?
06) Tem-se uma corda de massa 400 g e de
comprimento 5 m. Sabendo-se que está tracionada de
288 N,determine:
(A) Qual a freqüência das ondas?
(B) Caso o vibrador aumente apenas a sua amplitude
de vibração, o que ocorre com a velocidade de
propagação, o comprimento e a freqüência das
ondas?
a) a velocidade de propagação de um pulso nessas
condições;
b) a intensidade da força de tração nessa corda, para
que um pulso se propague com velocidade de 15 m/s.
04) (UMC-SP) A figura representa uma onda
harmônica que se propaga para a direita, com
velocidade de 20 m/s.
07) A figura representa um trem de ondas periódicas
propagando-se com velocidade de 10 m/s, em uma
corda AC, de densidade linear 2 . 10-1 kg/m. Essa corda
está associada a uma outra, CB, na qual a velocidade e
propagação do trem de ondas passa a ser de 20 m/s.
Pede-se:
Calcule:
(A) o comprimento de onda;
a) a intensidade da força que traciona a associação de
cordas;
(B) a amplitude;
b) a densidade linear da corda CB;
(C) a sua freqüência;
c) a freqüência da onda;
(D) o seu período.
d) o comprimento de onda na corda CB.
ramiltonfisica.blogspot.com
[email protected]
1
08) Uma corda, de massa m = 240 g e de
comprimento l = 1,2 m, vibra com freqüência de 150
Hz, no estado estacionário esquematizado. Determine
a velocidade de propagação da onda na corda e a
força tensora na mesma.
14) Determine a temperatura em ºC, na qual o valor
na escala Fahrenheit excede em 3 unidades o dobro
do valor na escala Celsius.
15) Um bloco de alumínio com 600g de massa deve
ser aquecido de 10ºC até 150ºC. Sendo de 0,22
cal/gºC o calor específico do alumínio, calcule:
(A) a quantidade de calor que o bloco deve receber;
(B) a sua capacidade térmica.
16)Quantas calorias perderá a massa de dois
quilogramas de água, quando a sua temperatura
baixar de 50ºC para 20ºC?
09) (F.M. Pouso Alegre-MG) O termômetro Celsius
marca 0 na temperatura do gelo fundente e 100 na
temperatura de ebulição da água, sob pressão
normal. O termômetro Fahrenheit marca 32 e 212;
respectivamente, nessas temperaturas. Quando o
termômetro Celsius marca 40ºC, o Fahrenheit
marcará:
17) Em um recipiente, colocamos 250 g de água a
100ºC e, em seguida, mais 1.000 g de água a 0ºC.
Admitindo que não haja perda de calor para o
recipiente e para o ambiente, calcule a temperatura
final das 1.250 g de água.
10) (Unimep-SP) Numa das regiões mais frias do
mundo, o termômetro indica –76ºF. Qual será o valor
dessa temperatura na escala Celsius?
18) Um bloco com 200 g de massa, a 100ºC, é
introduzido num calorímetro, de capacidade térmica
desprezível, que contém 500 g de água a 12ºC.
Determine o calor específico do metal que constitui o
bloco, sabendo-se que o equilíbrio térmico se
estabelece a 20ºC.
11) OSEC-SP) Uma temperatura na escala Fahrenheit é
expressa por um número que é o triplo do
correspondente na escala Celsius. Essa temperatura
em ºF é:
19) (UFAL) O calor latente do gelo é 80 cal/g e o calor
específico da água é 1 cal/gºC. Com estes dados podese concluir que o calor necessário para fundir 1 g de
gelo a 0ºC é suficiente para elevar, de 15ºC para 35ºC,
a temperatura de uma quantidade de água cuja a
massa, em gramas, é:
12) (UNIMEP-SP) Numa das regiões mais frias do
mundo, o termômetro indica –76ºF. Qual será o valor
dessa temperatura na escala Kelvin.
13) (UFAL) A temperatura de fusão do gelo é 0ºC. Essa
temperatura, na escala absoluta e escala fahrenheit, é
expressa, respectivamente, pelos valores:
(A) 5
(A) 80 e 32
(B) 4
(B) 0 e 273
(C) 3
(C) 32 e 273
(D) 2
(D) 273 e 32
(E) 1
(E) 32 e 80
20) (UFAL) O calor específico do chumbo é 0,31
cal/gºC. Em um trabalho científico, este valor deve ser
expresso, no Sistema Internacional, em J/ kg · K.
ramiltonfisica.blogspot.com
[email protected]
2
Lembrando que 1 cal 4,186 J, o calor específico do
chumbo é no S.I.
(A) 1,3 · 10-2
(B) 1,3 · 10-1
(C) 1,3 · 103
(D) 1,3 . 101
(E) 1,3 · 102
ramiltonfisica.blogspot.com
[email protected]
3