17 Podemos usar como termo de comparação - Moodle

!
Podemos usar como termo de comparação para os fluxos anuais de energia no
planeta Terra os indicadores relativos ao consumo energético mundial. Estas
estatísticas podem ser encontradas na Internet, fazendo uma busca em “World
Primary Energy Consumption”. Na página encontrada o consumo energético é
apresentado em
(
), uma unidade pouco usual de energia.
Para referência fica a sua equivalência ao
,
. As grandes
quantidades de energia são expressas em “quadriliões de Btu”, ou
, na
nomenclatura da mesma página. A sua equivalência em joule vale
=
=
×
Obtivemos assim os seguintes valores para os consumos observados em 1970 e
2001, assim como um consumo estimado para 2025
Ano
1970
2001
2025
Consumo anual (
207
404
623
)
Consumo anual (J)
20
2.2x10 J
20
4.3x10 J
20
6.6x10 J
7.1 A energia solar incidente no topo da atmosfera
Os satélites meteorológicos permitem
medir o fluxo de energia solar que
incide no topo da atmosfera, ΦRS ,
cujo valor é dado por
Φ =
Uma vez que esta energia é
proveniente
do
Sol,
podemos
considerar que ela incide como um
feixe paralelo no planeta Terra, como
se mostra na figura 18. Por isso, a
potência de radiação solar total
incidente em todo o Globo é dada
pelo produto do fluxo pela superfície de um disco com o raio da Terra (figura 18),
=Φ π
Usando
para o raio da Terra obtemos o valor de
=
×
6
Durante um ano, que perfaz um total de 31.56x10 s, a energia total de radiação
solar incidente no topo da atmosfera vale
=
×
Esta energia é cerca de 4000 vezes superior ao consumo energético mundial do ano
de 2001, que vimos anteriormente. Esta energia disponível livremente constitui um
dos maiores mananciais energéticos ainda por explorar de forma completa pela
humanidade. Se aproveitássemos apenas uma parte em 1000, todas as nossas
necessidades energéticas estariam resolvidas. Tal aproveitamento é por enquanto
uma miragem e as consequência do aproveitamento intensivo da energia solar na
Terra estão ainda longe de serem completamente apreciadas. Quando ao seu
aproveitamento no espaço, falta resolver o problema do transporte.
Cap.4-
17
!
7.2 A energia geotérmica
Apenas uma pequena parte da energia solar incidente no topo da atmosfera atinge
a superfície do planeta. Uma vez que, à escala geológica, a temperatura à superfície
se tem mantido aproximadamente constante, isto significa que o sistema Globo
deve emitir para o espaço uma quantidade equivalente de energia, por forma a se
manter um equilíbrio energético.
Essa energia é a energia geotérmica e tem a sua origem no interior do planeta. O
interior do planeta é muito mais quente que o seu exterior e a energia escapa por
condução e convecção. A elevada temperatura do planeta tem duas origens, por um
lado a energia residual da formação do planeta, há cerca de 4,5 bilhões de anos
atrás, e ainda a energia do decaimento radioactivo dos isótopos que compõem o
interior do planeta. Sem esta segunda componente, há muito que o interior do
planeta estaria frio e a Terra seria inabitável. Desconhecendo a existência da
radioactividade, o reputado físico inglês Thomson no século XIX estimou para a
idade da Terra um valor muito inferior ao dos Geólogos que usavam a observação
no terreno dos processos geológicos.
As medições realizadas à superfície da Terra permitem estimar um valor médio para
o fluxo geotérmico, ΦG
Φ =
=
O fluxo geotérmico varia muito de local para local tendo em conta o seu
enquadramento geodinâmico. Para o Globo inteiro, a potência total é agora obtida
multiplicando o fluxo pela superfície da Terra,
=Φ π =
×
Esta potência é cerca de 1000 vezes inferior à potência da radiação solar incidente
no topo da atmosfera. Durante um ano, a energia geotérmica total emitida pela
Terra vale
=
=
×
Comparando com o consumo energético em 2001, este valor é apenas o dobro
desse consumo, pelo que a energia geotérmica nunca se poderá estabelecer como
fonte alternativa de energia. Seria necessário aproveitar metade da energia
disponível.
7.3 A energia sísmica
Os sismos são sem dúvida uma das mais impressionantes manifestações do
planeta vivo que é a Terra. A dimensão dos sismos é medida pela magnitude.
Existem várias escalas de magnitude, que dependem da forma como são medidad,
sendo uma delas a magnitude Ms, media a partir da amplitude das ondas
superficiais. Gutenberg e Richter proposeram há mais de 50 anos uma relação entre
a energia sísmica (de vibração) libertada por um sismo e a magnitude Ms do
mesmo. Esta relação é ainda utilizada hoje em dia em sismologia,
=
+ !
Nesta expressão a energia está expressa em
. É devido a esta lei que podemos
dizer que quando a magnitude de um sismo aumenta de 1 grau, a energia libertada
Cap.4-
18
!
aumenta 30 vezes. A escala de energia é uma escala logarítmica. Se quisermos
saber a energia libertada por um sismo, basta fazer
!
=
As redes de observação mundial que existem em operação desde a década de 60
permitem registar hoje em dia todos os sismos com uma magnitude superior a 5.
Sabendo também que os sismos mais frequentes são os de menor magnitude, e
que quando a magnitude diminui de 1 grau, o número de sismos aumenta 10 vezes,
podemos estimar a energia sísmica total liberta na Terra durante um ano. Ela é
aproximadamente igual à energia de um sismo com magnitude ! " Usando a
expressão anterior, obtemos então para esta energia o valor de
=
×
Esta energia é 500 vezes inferior à energia geotérmica e cerca de 200 vezes inferior
ao consumo energético global no ano de 2001. O grande efeito dos sismos não se
deve à energia total envolvida, mas sim ao facto de essa energia ser libertada de
forma concentrada no espaço e no tempo, ao contrário da energia geotérmica.
7.4 A energia cinética das placas
A Geologia encontra-se hoje dominada pelo paradigma da Tectónica de Placas,
sendo difícil encontrar um domínio das Ciências da Terra onde ele não tenha
influência. Vamos por isso neste parágrafo estimar o valor médio da energia cinética
das placas tectónicas, usando a expressão
$
=
#
Começamos por admitir que a velocidade média das placas vale
$ % , isto é,
−
#= $
=
×
Para calcular a massa das placas, usaremos a sua expressão em função da
densidade e do volume, = ρ& . Usamos para a densidade o valor médio
ρ=
' $ =
'
Para o cálculo do volume, vamos considerar que esta é um paralelepípedo, com a
superfície do planeta Terra e uma espessura de (
.
& =) π =
×
A massa da litosfera toma assim o valor
= ρ& = ×
'
Substituindo agora todos os valores na expressão da energia cinética, obtemos
×
=
$ =
Este é um valor equivalente à energia contida em dois iogurtes! (ver ponto 2.8 neste
capítulo).
Para estimarmos a transferência de energia envolvida para manter estas placas em
movimento durante um ano, vamos admitir que elas se movem contra uma força de
atrito cinético, de coeficiente *$
. Nestas circunstâncias, para velocidade
constante, a potência dissipada pelo atrito vale
×
+ = +$ # = * $ ' # =
A energia envolvida ao longo de um ano inteiro vale
Cap.4-
19
+
=
×
.Trata-se de um
!
valor próximo da energia geotérmica, o que sugere uma forte relação entre os dois
processos, a cinemática de placas e o escape de energia do interior do planeta
Terra.
8. Impulso e Quantidade de Movimento
A 2ª lei de Newton que foi estudada anteriormente no capítulo da Dinâmica,
relacionando as causas do movimento (as forças) com os seus efeitos (uma
aceleração)
#
,=
=
aplica-se a corpos em que a massa se mantém constante. Existem no entanto
diversas situações em que existe movimento mas a massa não se mantém
constante:
Um balão cheio de ar. Quando deixamos o ar sair, o balão movimenta-se no
ar mas a sua massa não se mantém constante, o ar do interior é expulso
através da pequena abertura do balão.
Um foguete. Num foguete de fogo de artifício a combustão da pólvora faz
mover o corpo mas como consequência a massa do foguete diminui.
Um foguetão. Passa-se o mesmo que num foguete. O combustível do
foguetão é queimado e ejectado pelo que a massa do foguetão vai
diminuindo com o movimento. O princípio pode ser ilustrado por uma simples
garrafa de refrigerante, parcialmente cheia de água e com ar comprimido. A
expulsão da água diminui a massa do foguetão e fá-lo mover-se.
Um barco e uma metralhadora. Ao dispararmos uma metralhadora no interior
de um barco, a massa do corpo vai diminuindo e o barco vai-se deslocando
no sentido contrário ao dos disparos
Um astronauta no espaço. No espaço, um astronauta para se deslocar não
dispõe da gravidade e do atrito no chão para o ajudar. Ele socorre-se de
pequenos foguetes que vai disparando no sentido contrário ao que pretende
deslocar-se. Se numa nave espacial um astronauta se encontrar suspenso no
ar sem nada para se agarrar, o que ele deve fazer é pegar num objecto na
sua posse e atirá-lo com força numa direcção. O corpo será projectado na
direcção oposta, mas a sua massa terá diminuído.
Nenhuma destas situações é regida pelo enunciado da 2ª lei tal como o repetimos
em cima. Elas enquadram-se num enunciado mais geral dessa lei, que até coincide
com a forma original como Newton terá apresentado a sua lei. Sabendo que a
massa é constante, então ela pode ser incluída dentro do sinal de derivada da 2ª lei.
Obtemos assim uma nova expressão, mais geral que a anterior, e que é aplicável
também aos casos em que a massa é variável
#
#
,=
→
,=
A nova grandeza que aparece nesta lei, o produto da massa pela velocidade,
designa-se por quantidade de movimento, e a letra que a representa é a letra -= #
Trata-se de uma grandeza vectorial, com a mesma direcção e sentido que o vector
velocidade. No sistema internacional de unidades, SI, esta grandeza não tem uma
Cap.4-
20
!
unidade especial, exprimindo-se em ' % . Usando o conceito de quantidade de
movimento, a 2ª lei de Newton toma a forma mais geral
#
,=
=
Se a força aplicada for nula, então o corpo tem uma quantidade de movimento
constante
,=
-=$
Quando a força aplicada não é nula, tem-se então para dois instantes diferentes, tA
e tB que a variação da quantidade de movimento se exprime sob a forma de um
integral,
,=
→
-=,
→
∆- = ,
+
Nesta última expressão, o integral do produto da força pelo intervalo de tempo,
representa uma nova grandeza física, que designamos por impulso da força, e
representamos pela letra ..
. = ,
O impulso da força exprime-se no sistema SI de unidades por / . Devemos notar,
que sendo a variação da quantidade de movimento igual ao impulso da força,
ambas as grandezas devem ter unidades equivalentes. De facto, impulso e
quantidade de movimento podem-se exprimir de forma indiferente pelas unidades
' % ou / .
Quando uma força constante actua durante um intervalo de tempo ∆t, então o seu
impulso é dado simplesmente pelo produto
. = ,∆
O conceito de impulso da força é importante em situações em que a força actua
durante um intervalo de tempo muito curto, como seja por exemplo, a acção de uma
pancada. Neste caso, não importa saber o que se passa durante a pancada, mas
relacionar esta com a alteração do estado de movimento verificada. Isto é possível
de fazer através do conceito de impulso da força e quantidade de movimento
. = ∆- = - 0 − -
9. Conservação da Quantidade de Movimento
9.1 Um sistema de partículas
A conservação da quantidade de movimento de uma partícula é uma situação trivial,
que resulta directamente do enunciado da 2ª lei de Newton. No entanto, o mesmo já
não sucede para um sistema de partículas.
Para ilustrar o que sucede com um sistema de partículas consideremos a situação
descrita na figura 19. Podemos aqui ver um sistema formado por 4 partículas. Estas
partículas ir-se-ão mover sob a acção de forças que podem ser de dois tipos:
as forças interiores, que traduzem as interacções entre os componentes do
Cap.4-
21
!
sistema, ,
as forças exteriores, que traduzem a interacção entre o sistema e o seu
exterior, , 1
Se considerarmos agora a acção
global de todas as forças sobre o
sistema de partículas,
, = , + ,1
verificamos que, pela 3ª lei de
Newton, ou lei da acção e reacção, a
soma das forças interiores é nula,
, =
Por outro lado, a quantidade de
movimento é uma grandeza aditiva e
por isso a quantidade de movimento
do sistema de partículas é dado por
-=
Sendo assim, a 2ª lei de Newton, , = indica-nos que apenas as forças
exteriores podem alterar a quantidade de movimento total de um sistema de
partículas, ou seja, num sistema de partículas podemos escrever
,1 =
Quando a soma das forças exteriores for nula, então há conservação da quantidade
de movimento, mesmo que existam forças interiores. Este é o teorema da
conservação da quantidade de movimento: quando a resultante das forças
exteriores aplicadas a um sistema de partículas for nula, então a quantidade de
movimento do sistema mantém-se constante
,1 =
-=
- =$
ou
.
1
=
-=
- =$
Este é o princípio que permite explicar o movimento dos corpos apresentados no
início do parágrafo 8. Vejamos por exemplo o caso do astronauta. Ele está
inicialmente em repouso e a sua quantidade de movimento é nula. Quando dispara
um jacto numa direcção, a força envolvida é uma força interior, pois o combustível
faz parte do sistema. No entanto, ao projectar uma massa de gás a alta velocidade
numa dada direcção, faz esta ganhar quantidade de movimento nessa direcção.
Uma vez que não há forças exteriores, a quantidade de movimento total deve-se
manter nula. Isso só é possível se o corpo do astronauta for projectado na direcção
oposta. A mesma interpretação se aplica ao exemplo do foguetão no espaço ou à
metralhadora no interior de um barco.
Cap.4-
22
!
9.2 Choques e explosões
O teorema da conservação da quantidade de movimento também se aplica a um
outro conjunto de situações, que podemos designar por choques e explosões.
Estas situações ocorrem habitualmente na presença do peso ou de outras forças
exteriores. No entanto, a interacção é tão rápida, que podemos considerar que o
impulso das forças exteriores também é nulo, isto é,
∆ ≈
. 1 ≈,1 ∆ ≈
Então, nestas situações, também podemos considerar que a quantidade de
movimento do sistema de partículas se mantém constante.
Resumindo, temos duas situações em que há conservação da quantidade de
movimento de um sistema de partículas:
,1 =
quando a resultante das forças exteriores é nula
quando o tempo da interacção é tão rápido que o impulso das forças
exteriores é nulo . 1 ≈ , 1 ∆ ≈
Nos choques e explosões, uma vez que se admite que as interacções são
instantâneas ( ∆ ≈ ) então também se verifique que entre os instantes
imediatamente antes e imediatamente depois do choque (ou explosão) a posição
das partículas não sofreu alteração. Isto significa que, sendo a energia potencial
função exclusiva da posição, num choque ou explosão não há variação da energia
potencial. Por isso, num choque ou explosão apenas pode haver variação da
energia cinética total das partículas.
Vamos assim classificar os choques quanto à variação da energia cinética. Um
choque é elástico quando durante o choque não há variação da energia cinética,
isto é, a energia cinética mantém-se constante (e por consequência também a
energia mecânica se mantém constante, pelas considerações anteriores)
∆ $=
→
= $
$
$ 0
Um choque diz-se inelástico quando há uma diminuição da energia cinética
durante o choque
∆ $<
→
< $
$
$ 0
Neste caso diz-se que há dissipação de energia.
Há ainda um outro tipo de choque que merece uma designação especial, trata-se do
choque perfeitamente inelástico. Esta classificação aplica-se aos casos em que
os corpos após o choque se movem com a mesma velocidade final, os corpos ficam
ligados uns aos outros.
9.3 Exemplos de aplicação
Choque frontal elástico
Neste caso consideramos o choque entre duas massas iguais, estando uma delas
inicialmente em repouso. O choque é frontal, o que significa que no final as bolas se
devem deslocar na mesma direcção e sentido que a bola incidente. Esta situação
Cap.4-
23
!
encontra-se descrita na figura 20. Trata-se de um caso frequente em jogos como o
bilhar ou o “curling”, um jogo que se faz com pedras cilíndricas que se deslocam
escorregando numa pista de gelo.
Devemos notar que as velocidades depois do choque de cada uma das partículas
se identifica com uma ’ (plica).
Tratando-se de um choque, há conservação da quantidade de movimento entre os
instantes imediatamente antes e imediatamente depois do choque. Essa não é a
situação representada na figura, onde as partículas se ilustram afastadas uma da
outra, para facilitar a identificação dos vectores velocidade relevantes. Temos então
=- →
# = # + #
Usando o eixo XX indicado na figura, esta equação vectorial traduz-se na seguinte
equação escalar
# = # + #
Sendo o choque elástico, devemos ainda observar a conservação da energia
cinética, o que se traduz na equação
$
=
$
-
→
# =
# +
#
Conjugando as duas equações, obtemos um sistema de duas equações a duas
incógnitas, as velocidades das bolas após o choque,
# = # + #
# = # +#
→
# =
# +
#
# = # +#
Substituindo a 1ª equação na segunda obtemos
# + # + # # = # +#
→
# # =
Esta equação tem 3 soluções possíveis:
ambas as velocidades são nulas, não é possível fisicamente, violaria a
conservação da energia cinética
a velocidade final da bola 2 seria nula, # = . Esta solução também não é
fisicamente possível, pois significaria que a bola 1 atravessaria a bola 2 como
um fantasma sem a tocar
a velocidade final da bola 2 é nula, # = . É a única solução fisicamente
possível.
Usando agora a conservação da quantidade de movimento para obter a velocidade
final da bola 2, obtemos a solução completa do nosso problema
# =
# =
Num choque frontal elástico entre bolas da mesma massa, estando uma delas
parada, há uma transferência integral da velocidade da bola que se move para a
bola parada. Esta passa a mover-se exactamente com a mesma velocidade.
Cap.4-
24
!
Esta propriedade dos choques elásticos é usada num objecto decorativo que é
habitualmente designado por pêndulo de Newton. Trata-se de um conjunto de
esferas metálicas em contacto umas com as outras e suspensas por fios. Quando
se afasta uma das bolas de forma que ela vá bater na mais próxima, o choque é
comunicado em sucessão a todas as bolas, movendo-se apenas a última esfera da
série, que assim inicia um novo ciclo.
Bola elástica que bate no chão
Trata-se de uma situação que facilmente
podemos experimentar com qualquer tipo de
bola, uma bola de basquete, uma bola de ténis
ou uma “super-bola” de borracha. Quando
deixamos cair qualquer destas bolas no chão,
ela é reflectida sendo devolvida pelo choque
com uma velocidade que é quase idêntica à
velocidade incidente, de tal forma que a bola
quase que atinge a altura inicial do
lançamento. O efeito é mais evidente no caso
da “super-bola”. Vejamos como é que tal
situação é possível, admitindo que o choque no chão é elástico. A situação que
pretendemos estudar encontra-se descrita na figura 22.
Tal como anteriormente, trata-se de um choque frontal elástico e por isso devem-se
aplicar dois princípios de conservação, a conservação da quantidade de movimento
(choque) e a conservação da energia cinética (elástico). A diferença em relação ao
caso estudado anteriormente reside no facto de neste caso a massa dos dois
objectos ser diferente, sendo a massa do corpo (1) muito menor que a do corpo (2)
<< !
Começando pela conservação da quantidade de movimento, obtemos a seguinte
equação vectorial
=- →
# = # + !#
Usando o eixo YY indicado na figura 22, esta equação vectorial traduz-se na
equação escalar
− # = # − !#
Como o choque é elástico há conservação da energia cinética e podemos escrever
a equação
Cap.4-
25
!
$
=
$
→
-
# =
# + !#
Conjugando as duas equações, obtemos um sistema de duas equações a duas
incógnitas, as velocidades das bolas após o choque,
− # = # − !#
# =
# + !#
Uma vez que as massas são diferentes, este sistema não pode ser facilmente
simplificado. Para o resolver vamos dividir ambas as equações pela massa da Terra
M, designando o quociente entre massas pela letra α, que pelas condições do
problema, deve ser muito menor que 1,
α=
<< !
α <<
!
Usando este factor e cortando também o factor 2 na equação da energia cinética,
obtemos o sistema de equações
− α# = α# − #
# = α# + α# = α # + #
α# = α# + #
−
Substituindo agora na 2ª equação obtemos
α# = α# +α # + #
→
# = # +α # + #
α
<<
Usando o facto de
podemos nesta equação desprezar a 2ª parcela do
segundo termo e escrevermos
# ≈#
Isto é, a velocidade final da bola é igual, em módulo, à velocidade inicial da bola,
mas tem o sentido oposto,
# ≈ −#
Verificamos assim que o choque elástico de uma bola com a Terra devia fazer esta
voltar a atingir a altura de lançamento. Se desprezarmos o atrito durante o trajecto, a
diferença de alturas verificada nos casos reais traduz a perda de energia cinética
durante o choque inelástico.
Choque perfeitamente inelástico
Trata-se de uma situação em que
após o choque ambos os corpos
ficam com a mesma velocidade final,
deslocam-se em conjunto. Esta é, por
exemplo, a situação que se verifica
quando um asteróide choca com a
Terra.
Este
caso
encontra-se
ilustrado na figura 23.
Neste caso não há conservação de
energia cinética, apenas conservação da quantidade de movimento, verificando-se
ainda que
# =# =#
Uma vez que o corpo 2 se encontra inicialmente em repouso, podemos escrever
Cap.4-
26
!
equação vectorial
=- →
# = +! #
Usando o eixo XX indicado na figura 23, esta equação vectorial traduz-se na
equação
# =
+! #
→
# =#
+!
2
Vejamos por exemplo o caso de uma asteróide, de densidade ('%
$ e com um raio
, que embate na Terra com uma velocidade de 3
de
%. A massa da Terra é
aproximadamente
3× 3 '. A massa do asteróide vem dada por
= ρ& = ρ
π
=
×
'
Usando a expressão obtida anteriormente, obtemos para a velocidade final do
conjunto Terra+asteróide a velocidade de
# =#
=
×
−
+!
Trata-se de uma velocidade muitíssimo pequena!
=
Choque oblíquo com massas iguais
Trata-se de uma situação análoga ao primeiro exemplo estudado, em que duas
bolas de massas iguais chocam, estando uma delas inicialmente em repouso. Neste
caso o choque não é frontal e por isso no final cada bola vai para o seu lado, como
se mostra na figura 24.
À semelhança das situações anteriores, a conservação da quantidade de
movimento durante o choque em simultâneo com a conservação da energia cinética,
por ser um choque elástico, permitem escrever o seguinte sistema de equações, em
que a 1ª é uma equação vectorial e a 2ª uma equação escalar,
# = # + #
# = # +#
→
# =
# +
#
# = # +#
Cap.4-
27
!
Usando a 1ª equação e as propriedades do produto interno, podemos calcular o
quadrado do módulo da velocidade # como
# = # ⋅ # = # +# ⋅ # +# = # +# + # ⋅#
Substituindo na equação de conservação da energia cinética obtém-se
# +# + # ⋅# = # +#
# ⋅# =
Isto é, se nenhuma das velocidades finais for nula, então a nulidade do produto
interno implica que as velocidades das bolas após o choque são perpendiculares
# ⊥#
→
α +β =
→
β= β
α=
β
Para resolver um caso concreto há que decompor
cada uma das velocidades finais no sistema de
eixos XY, como se indica na figura 25.
A equação vectorial da conservação da quantidade
de movimento transforma-se num sistema de duas
equações escalares
# =#
α +#
β
=#
α −#
β
Se considerarmos as relações trigonométricas entre
os ângulos α e β, assim como a conservação de
energia cinética, obtemos um sistema de 3 equações
# = # +#
# =#
α +#
α
=#
α −#
α
Este sistema tem 3 incógnitas, as velocidades #4 , #43 e o ângulo α, se soubermos a
velocidade inicial # . Sucede, no entanto, que estas 3 equações não são
independentes e por isso apenas duas incógnitas podem ser determinadas. Por
isso, neste tipo de problemas é necessário dar o valor final de uma das 3 incógnitas,
habitualmente um dos ângulos de saída, α ou β.
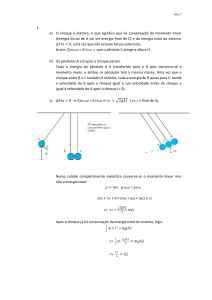
Conservação de energia e de quantidade de movimento
Neste
capítulo
foram
enunciados dois grandes
princípios de conservação
da Física, a conservação de
energia e a conservação da
quantidade de movimento.
No exemplo que iremos
agora
desenvolver
ilustramos uma situação
onde ambos os princípios se
devem aplicar.
Consideremos então dois pêndulos com massas diferentes mas dispostos de tal
maneira que podem chocar de forma frontal, como se mostra na figura 26. Do
Cap.4-
28
!
sistema conhecemos as massas dos pêndulos,
e !, assim como a altura de
lançamento do pêndulo mais pequeno, . O pêndulo cai ganhando velocidade e vai
bater no pêndulo maior. O choque que se dá é frontal e elástico. Como
consequência ambos os pêndulos ganham uma velocidade o que lhes vai permitir
atingir no seu movimento as alturas máximas de 4e 54, respectivamente para o
pêndulo pequeno e pêndulo grande.
O objectivo deste problema consiste em determinar o valor das alturas finais de
cada um dos pêndulos em função dos dados do problema. Para resolver esta
questão, temos de decompor o movimento global numa sequência de movimentos
que sejam tratáveis pelas leis da Física conhecidas.
1º movimento, a queda do pêndulo pequeno.
Na ausência de atrito, este movimento processa-se com conservação da energia
mecânica pois as únicas forças a actuar são o peso, uma força conservativa, e a
tensão no fio, que não realiza trabalho. Sabemos então que a energia mecânica no
ponto mais alto da trajectória, com velocidade nula, deve ser igual à energia
mecânica no seu ponto mais baixo. Tomando o ponto mais baixo do centro do
pêndulo como referência para a energia potencial gravítica do peso, podemos
escrever
' =
→
#
#=
'
Nesta equação # representa a velocidade do pêndulo pequeno imediatamente antes
de este embater no pêndulo grande.
2º movimento, choque frontal elástico entre os pêndulos.
A figura 27 ilustra a disposição das
velocidades para esta situação. A
conservação da quantidade de
movimento durante o choque
permite escrever a equação
vectorial
# = # + !&
Usando o eixo XX indicado na
figura, esta equação vectorial
traduz-se na equação escalar
# = − # + !&
Sendo o choque elástico, há que observar a conservação da energia cinética
$
=
$
-
→
# =
# + !&
Conjugando as duas equações, obtemos um sistema de duas equações a duas
incógnitas, as velocidades das bolas após o choque,
# = − # + !&
# = −# +α&
→
# =
# + !&
# = # +α&
Neste caso dividimos ambas as equações pela massa do pêndulo mais pequeno,
Cap.4-
29
,
!
e designámos o quociente das massas pela razão α = !
.
Para resolver o sistema vamos usar o método da substituição. Pegando na 1ª
equação podemos escrever
# = − # + α&
→
# = # + α & − α#&
Substituindo agora na 2ª equação temos, após simplificação,
# = # + α & − α#& +α&
→
α#& = α & +α&
→
# =& α +
Obtemos então finalmente a solução para a velocidade após o choque do pêndulo
maior
& =#
+α
Usando agora a 1ª equação do sistema, obtemos também a velocidade final do
pêndulo pequeno
α−
# = − # + α&
→
# =#
+α
3º movimento, a subida do pêndulo maior.
Tal como o primeiro movimento, esta subida processa-se, na ausência de atrito,
com conservação da energia mecânica, pelas mesmas razões que foram apontadas
anteriormente. Usando de novo como referência o ponto mais baixo do centro do
pêndulo, podemos escrever para a conservação de energia mecânica a expressão
que resulta de se igualar as energias dos pontos mais baixo e mais alto da
trajectória (onde a velocidade é nula)
&
!& = !'5
→
5=
'
Usando as expressões já determinadas anteriormente, podemos escrever
#
5=
=
' +α
+α
4º movimento, a subida do pêndulo pequeno.
Tal como anteriormente, esta subida processa-se, na ausência de atrito, com
conservação da energia mecânica. Usando como referência o ponto mais baixo do
centro do pêndulo, podemos escrever para a conservação de energia mecânica a
expressão que resulta de se igualar as energias dos pontos mais baixo e mais alto
da trajectória (onde a velocidade é nula)
#
# = '
→
=
'
Usando as expressões já determinadas anteriormente, podemos escrever
# α−
α−
=
=
' +α
+α
Para exemplificar os resultados possíveis deste problema, vejamos o que sucede
para 3 razões diferentes entre as massas, de 10, 100 e 100 vezes. Os resultados
estão apresentados na tabela seguinte.
Cap.4-
30
!
α
10
100
1000
h’
0.67h
0.96h
0.996h
H’
0.033h
0.00039h
-6
4.0x10 h
Para uma grande diferença entre as massas, o pêndulo pequeno praticamente
atinge a altura de lançamento inicial.
Cap.4-
31