notas de aula

*
NOTAS DE AULA
RESOLUÇÃO DE PROBLEMAS
Benedito Tadeu Vasconcelos Freire
NOTAS DE AULAS COMPLEMENTARES - SEDIS. UFRN
WWW. SEDIS . UFRN . BR
Notas de Aulas complementares para os alunos do Curso de Especialização em Ensino de Matemática para o
Ensino Médio, realizado de janeiro a dezembro de 2015.
Primeira Versão, Setembro de 2015
Conteúdo
1
Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2
ESTRATÉGIAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.0.1
2.0.2
Antes de fazer, tente entender! . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
A busca do plano . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.1
Procure semelhanças com outros problemas.
2.1.1
Aplicação 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
8
2.2
Começar pelo fácil torna fácil o difícil
10
2.3
Experimente, procure algo que seja invariante
10
2.3.1
Aplicação 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.4
Faça um desenho e, dependendo da situação, pinte às cores.
12
2.5
Modifique o enunciado, para ver se lhe ocorre um caminho possível
14
2.5.1
Aplicação 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14
2.6
Redução ao Absurdo.
16
2.7
Suponha o problema resolvido (ou olhe de trás para diante)
17
2.7.1
Aplicação 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 17
3
Problemas Diversos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21
4
Legenda . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
4.1
Legenda
5
Bibliografia . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
31
1. Introdução
Da prática da nossa convivência com os estudantes, verificamos que a maioria deles não tem facilidade
para resolver problemas. Estas notas pretendem mostrar algumas idéias que poderão apontar ao estudante
caminhos facilitadores no sentido de tornar a atividade de resolução de problemas menos árida.
Para resolver problemas de forma clara, o estudante tem que comunicar suas idéias de maneira coerente,
com organização e com argumentos estruturados, permitindo a ele próprio e aos outros o entendimento fácil
de seus argumentos e a intrepretação perfeita de suas idéias.
A Matemática é a linguagem apropriada para a resolução de problemas nas diversas áreas do conhecimento, por ser concisa, ter muitos recursos e não permitir ambiguidades.
Galileu Galilei 1 foi quem introduziu a matemática como linguagem da ciência.
Como um reconhecimento por suas qualidades indispensáveis à formação do cidadão, a Matemática é a
única disciplina que é estudada em todos os países do mundo e em todos os níveis educacionais.
De acordo com Paul Halmos 2 , o coração da matemática são seus próprios problemas. "A maior parte de
1 GALILEU GALILEI Galileu Galilei (1564 -1642 ), italiano, foi um físico, matemático, astrônomo e filósofo. Galileu Galilei foi
personalidade fundamental na revolução científica. Foi o mais velho dos sete filhos do músico italiano, alaudista, Vincenzo Galilei e de
Giulia Ammannati. Viveu a maior parte de sua vida em Pisa e em Florença, na época integrantes do Grão-Ducado da Toscana.
Galileu Galilei desenvolveu os primeiros estudos sistemáticos do movimento uniformemente acelerado e do movimento do pêndulo.
Descobriu a lei dos corpos, enunciou o princípio da inércia e o conceito de referencial inercial, idéias precursoras da mecânica
newtoniana. Galileu melhorou significativamente o telescópio refrator e com ele descobriu as manchas solares, as montanhas da Lua,
as fases de Vénus, quatro dos satélites de Júpiter, os anéis de Saturno, as estrelas da Via Láctea. Estas descobertas contribuíram
decisivamente na defesa do heliocentrismo. Contudo a principal contribuição de Galileu foi para o método científico, pois a ciência
assentava numa metodologia aristotélica.
O físico desenvolveu ainda vários instrumentos como a balança hidrostática, um tipo de compasso geométrico que permitia medir
ângulos e áreas, o termómetro de Galileu e o precursor do relógio de pêndulo. O método empírico, defendido por Galileu, constitui
um corte com o método aristotélico mais abstrato utilizado nessa época, devido a isto Galileu é considerado como o "pai da ciência
moderna". Fonte: htt p : //pt.wikipedia.org/wiki/GalileuG alilei. Acessado em 17/03/2014.
2 PAUL HALMOS - (1916 - 2006) foi um matemático estadunidense nascido na Hungria, que fez avanços fundamentais nas áreas
de Lógica Matemática, Teoria da Probabilidade, Estatística, Teoria dos Operadores, Teoria Ergódica e Análise Funcional (em especial,
nos espaços de Hilbert ). Ele também foi reconhecido como um grande expositor da matemática.
Halmos chegou em os EUA aos 13 anos de idade, mas nunca perdeu seu sotaque húngaro. Halmos obteve seu Bacharelado na
Universidade de Illinois, graduando em filosofia e especializando-se em matemática. Ele levou apenas três anos para obter o grau, e
tinha apenas 19 anos quando se formou. Começou um doutorado (Ph.D.) na filosofia, mas, passou para a matemática, graduando-se em
Capítulo 1. Introdução
6
cada vida significativa é passada com a solução de problemas; uma parte considerável da vida profissional de
técnicos, engenheiros, cientistas, etc., é vivida na busca de solução de problemas de matemática. É dever de
todos os professores e dos professores de matemática em particular, expor seus alunos para problemas muito
mais do que aos fatos", disse ele.
O uso da Matemática com linguagem exige um conhecimento mínimo para poder ser utilizada. Por isso,
o estudante necessita de situações que permitam exercitar essa linguagem, e uma delas são os empregos dos
métodos de resolução de problema.
Uma referência no estudo da arte de resolver problema são os trabalhos do professor Polya 3
Para oportunizar a resolução de problemas, apresentamos no texto problemas de Olimpíada de Matemática de vários países, por serem intrigantes, criativos e desafiadores.
É comum uma diferenciação entre problema e exercício, veja, por exemplo em [6], página x. O exercício é
uma questão que testa o domínio do estudante numa técnica que está sendo focada ou que foi recentemente
coberta. Exercícios podem ser difíceis ou fáceis, mas, de uma maneira geral, eles nunca são intrigantes, e
normalmente fica claro como proceder no sentido de como encontrar a solução. Por outro lado, um problema
é uma questão que não pode ser respondida imediatamente. Problemas são muitas vezes abertos, paradoxais,
às vezes indecifráveis e exigem investigação antes que se pode chegar a uma solução.
Esperamos que os estudantes possam apreciar as idéias que permitem a resolução dos problemas aqui
apresentados.
Todos os erros e equívocos são de nossa responsabilidade. Receberemos com alegria comentários
apontando eventuais erros, como também formas de melhorar o texto.
Natal, setembro de 2015
Benedito Tadeu Vasconcelos Freire
[email protected]
1938 sob a orientação do Professor Joseph L. Doob, com a dissertação intitulada: A Invariantes de Certas Transformações Estocásticos:
A Teoria Matemática de Sistemas de Jogos.
Pouco depois de sua formatura, Halmos foi para o Instituto de Estudos Avançados. Seis meses depois, ele estava trabalhando com John
von Neumann, que se revelou uma experiência decisiva. Na sua permaneência no Instituto de Estudos Avançados, Halmos escreveu seu
primeiro livro, Espaços Vetoriais de Dimensões Infinitas, que imediatamente estabeleceu sua reputação como um excelente expositor da
matemática.
Halmos ensinou na Universidade de Syracuse , na Universidade de Chicago (1946-1960), na Universidade de Michigan, na Universidade
da Califórnia, em Santa Barbara (1976-1978), na Universidade do Havaí, e na Universidade de Indiana, onde se aposentou. Desde
sua aposentadoria, em 1985, até sua morte, ele era ligado ao departamento de Matemática da Universidade de Santa Clara. Fonte:
http://en.wikipedia.org/wiki/PaulH almos.Acessadoem17/03/2014.
3 GEORG POLYA - George Pólya (1887 —1985) húngaro, professor de matemática de 1914 a 1940 no Instituto Federal de
Tecnologia de Zurique, na Suíça, de 1940 a 1953 na Stanford University, nos Estados Unidos. Pólya permaneceu como Professor
Emérito da Stanford o resto de sua vida e carreira. Ele trabalhou em uma variedade de tópicos matemáticos, incluindo séries, teoria dos
números, análise matemática, geometria, álgebra, combinatória e probabilidade.
No início de sua carreira, Pólya escreveu com Gábor Szegó, matemático húngaro famoso, dois influentes livros de problemas: Problemas
e Teoremas em Análise (I: Série, Cálculo Integral, Teoria das Funções e II, Teoria das Funções, Zeros de polinômios, Determinantes,
Teoria dos Números ,Geometria.....). Mais tarde, ele se dedicou ao estudo da Heurística, um método ou processo criado com o objetivo
de encontrar soluções para um problema, para identificar métodos sistemáticos de resolução de problemas a uma maior descoberta e
invenção em matemática para os estudantes, professores e pesquisadores. Ele escreveu cinco livros sobre o assunto: How to Solve it,
traduzido para o português como A Arte de Resolver Problema, Matemática e Raciocínio Plausível (Volume I: Indução e Analogia em
Matemática, e Volume II: Padrões de Plausível Inference) e descoberta matemática: Na compreensão, aprendizado e ensino Problem
Solving (volumes 1 e 2).
Em How to Solve It, Pólya fornece sugestões heurísticas para resolver uma gama de problemas, incluindo os problemas matemáticos e
os não-matemáticos. O livro inclui conselhos para ensinar os alunos de matemática e uma mini-enciclopédia de termos heurísticos. Foi
traduzido para várias línguas e já vendeu mais de um milhão de cópias. O físico russo Zhores I. Alfyorov, (Prêmio Nobel em 2000),
elogiou, lembrando que ele era um fã. O livro ainda é usado em educação matemática.
Além de suas obras que abordam diretamente a resolução de problemas, Pólya escreveu outro livro chamado Métodos Matemáticos em
Ciências, com base em um trabalho de 1963 apoiado pela National Science Foundation, editado por Leon Bowden, e publicado pela
Associação Matemática da América (MAA), em 1977. FONTE: htt p : //en.wikipedia.org/wiki/GeorgeP olya.
2. ESTRATÉGIAS
Já é clássica e bem conhecida, a formulação que fez Polya das quatro etapas essenciais para a resolução de
um problema, que constituem o ponto de partida de todos os estudos posteriores:
• Antes de fazer, tente entender
• Traçar um plano para resolvê-lo
• Colocar o plano em prática
• Comprovar os resultados
No que se segue, vamos desenvolver estas etapas, exercitando a resolução de problemas.
2.0.1
Antes de fazer, tente entender!
Quando alguém lhe propõe um problema, um jogo, um quebra-cabeça, inicialmente, assegure-se que entendeu
a fundo os dados do problema, as regras do jogo e o possível lugar que tem cada uma dessas informações,
como elas se encaixam umas com as outras. Para resolver um problema, é imprescindível que você conheça
o que é dado e, exatamente, o que o problema pede.
Faça a si mesmo as seguintes perguntas:
• Qual é a incógnita?
• Quais são as quantidades dadas?
• Quais são as condições dadas?
• O que o problema pede?
A solução do problema consiste em ligar, por passos lógicos, os dados do problema ao que nele se
pede .
R
2.0.2
A solução do problema consiste em ligar, por passos lógicos, os dados do problema ao que nele se
pede .
A busca do plano
Uma das técnicas de criatividade, chamada tempestade de idéias (em inglês brainstorming), geralmente feita
em grupo, revela que a quantidade gera a qualidade. O método foi popularizado nos anos de 1930 pelo
americano Alex Faicney Osborn. A fase em que você procura um plano capaz de levar a solução de um
problema é uma situação parecida com a tempestade de idéia, só que exercida muitas vezes solitariamente
por você. Esta fase do processo de resolução do problema é aquela em que deve nascer da sua cabeça
muitas idéias, mesmo que possam parecer totalmente inócuas.
Durante este processo, nenhuma idéia deve ser descartada ou julgada como errada ou absurda. As vezes, as
Capítulo 2. ESTRATÉGIAS
8
idéias em que você menos aposta podem se revelar as mais apropriadas. Por isso, anote todas as suas idéias.
Se você já tem algumas estratégias possíveis para atacar o problema, a tarefa a seguir é meditar sobre
as suas idéias e deixar que o seu subconsciente trabalhe, a seu gosto, esse amontoado de idéias que você
preparou para ele. É aconselhável que você faça uma lista das melhores idéias, a princípio sem misturá-las.
Explore cada idéia da lista com decisão e confiança, de forma ordenada, em paz, sem precipitações.
Se, ao colocar em prática uma idéia, lhe ocorrer outra, totalmente desligada da primeira, e que você avalia
que pode lhe ajudar, não vá desprezá-la. Coloque-a na sua lista. Mas, também não desvie sua atenção da
que agora está explorando.
Um ponto importante que deve sempre ser lembrado: você não pode desistir facilmente. Por outro lado,
não deve teimar demais só com uma idéia. Se as coisas complicarem demais, haverá provavelmente outro
caminho. Um caminho que foi muito usado na história de matemática foi o da tentativa e erro, tentativa e
erro, tentativa e erro, você não pode esquecer este fato.
Ao concluir sua resolução, você precisa ter certeza disso. Reveja sua solução com cuidado.
Uma verdade: as meias idéias e as meias soluções de pouco servem!
É preciso certificar de que, realmente, você chegou à solução.
Se você conseguir resolver o problema, ótimo.
Se trabalhou horas a fio e não conseguiu vislumbrar uma solução, não se preocupe. Muitas vezes se aprende
profundamente com os problemas que se tenta, com interesse, determinação e persistência ...... e não se
consegue resolver, do que com os que se resolve à primeira vista.
Um conselho deve ser lembrado: é mais importante a qualidade do que a quantidade. Não se apresse em
demasia. Ao concluir a solução de um problema, é preciso que você reflita sobre o processo, para que tenha
uma idéia das dificuldades, dos becos sem saídas em que se meteu e, principalmente, como deve proceder no
futuro para resolver melhor outros problemas, parecidos ou não.
Uma reflexão sobe o nosso próprio processo de pensamento é interessante na medida em que podemos
tirar bons proveitos para o futuro. Cada um tem seu próprio estilo de conhecimento. Visual ou analítico?
Depende muito da expressão verbal ou da forma escrita? Tem tendência para o compromisso com idéia
única, sem flexibilidade? Tem tendência a pensar em círculo obsessivamente? Como se pode fomentar o
fluxo de idéias novas, variadas, originais? Reflexões como essas ajudam, a saber, que tipo de problemas
você pode se ocupar com sucesso e em quais deles sua probabilidade de êxito não é tão grande.
2.1
Procure semelhanças com outros problemas.
Como não há nada de novo debaixo do céu, é conveniente procurar semelhanças do problema dado com
outros que você já conhece.
Pergunte a si mesmo: o que é que esse problema me faz lembrar?
Se seu problema for genérico, tente primeiro alguns casos particulares. Caso o problema envolva a geometria
tridimensional, você poderá tentar primeiro um problema bidimensional análogo.
2.1.1
Aplicação 1
Problema 2.1.1 - Resolva a equação x4 − 5x2 + 6 = 0.
Solução
Se a equação dada parece difícil, troque x2 por t, obtendo a equação
t 2 − 5t + 6 = 0
(∗),
2
que é mais fácil de resolver. Assim, as soluções da equação
(*) são
√
√ t = 2 e t = 3, o que implica x = 2 ou
2
x = 3. Portanto, as soluções da equação dada são: ± 2 e ± 3.
Problema 2.1.2 - Numa caixa retangular fechada, veja Figura a seguir, no vértice A temos uma formiga e
no vértice B temos outra formiga. A formiga na posição A quer encontrar a formiga na posição B.
Qual é o caminho mais curto sobre a caixa, ligando A até B?
Solução
2.1 Procure semelhanças com outros problemas.
9
O que é que esse problema me faz lembrar?
Se a questão fosse num retângulo, figura plana, em vez de uma caixa retangular, figura tridimensional,
a questão seria resolvida simplesmente procurando o menor caminho sobre o plano ligando dois pontos,
que sabemos ser um segmento de reta. O que temos que fazer é tornar a caixa tridimensional um objeto
bidimensional. Como fazer isso? Abrindo a caixa, marcando os dois pontos e traçando o segmento de reta
ligando os pontos A e B, veja figura a seguir.
Depois disso, recompomos a caixa, mostrando o menor caminho ligando os pontos A e B, veja figura a
seguir.
Problema 2.1.3 - Qual é a soma dos n termos da séries 7 + 77 + 777 + 7777 + · · · ?
Solução
Se em vez de 7 + 77 + 777 + 7777 + · · · tivéssemos
9 + 99 + 999 + 9999 + · · ·?
Neste caso, reescreveríamos a séries como:
9 + 99 + 999 + 9999 + · · · = (10 − 1) + (100 − 1) + (1000 − 1) + (10000 − 1) + · · · =
= (10 + 100 + 1000 + 10000 + · · · ) − n
As potências de 10 formam uma progressão geométrica de n termos cuja soma é igual a
10n+1 −10
.
9
Assim,
9 + 99 + 999 + 9999 + · · · =
= (10 − 1) + (100 − 1) + (1000 − 1) + (10000 − 1) + · · · =
10n+1 − 10
− n.
9
Agora, observe que para encontrar a soma pedida, basta observar que 7 é igual a
a soma pedida é igual a
7
9
de 9, o que implica que
7
× 9(1 + 11 + 111 + 1111 + · · · ) =
9
n+1
7
10
− 10
7
= (9 + 99 + 999 + 9999 + · · · ) =
− n = (10n+1 − 9n − 10).
9
9
81
7 + 77 + 777 + 7777 + · · · = 7(1 + 11 + 111 + 1111 + · · · ) =
Problema 2.1.4 - Numa sala de aula existem 25 alunos sentados em 5 filas com 5 lugares em cada fila. Um
dia o professor pede aos alunos para mudar os lugares como segue:
cada aluno deve mover um assento para a frente ou para trás ou um assento à esquerda ou à direita movimento em diagonal não é permitido.
É possível que todos os 25 alunos sigam estas instruções?
Solução
A abordagem tradicional é tentar vários movimentos. Isso geralmente não resolve o problem e causa
certa frustração. A idéia aqui é resolver um problema análogo mais simples. Assim, faça um desenho da
sala e numere os assentos, veja figura a seguir.
Agora, observe que, dos números inteiros de 1 a 25, temos 13 números ímpares e somente 12 números
pares. Com os movimentos permitidos, cada aluno passa de uma cadeira de número ímpar para uma cadeira
de número par, e vice-versa. Como a quantidade de números pares difere da quantidade de números ímpares,
vai haver um aluno que que não pode se movimentar.
Portanto, é impossível que todos os 25 alunos sigam as instruções do professor.
Capítulo 2. ESTRATÉGIAS
10
2.2
Começar pelo fácil torna fácil o difícil
Talvez o problema seja complicado porque há muitos elementos. Tente tornar o problema mais fácil. Construa um, menos complicado, com menos dados. Talvez essa situação venha lhe revelar algo que facilite a
solução do problema mais complexo.
Problema 2.2.1 - (BW - 2005) É possível encontrar 2014 números inteiros positivos distintos, cada um
deles um quadrado perfeito, tal que a soma seja também um quadrado perfeito?
Solução
A resposta é sim.
Se o problema fosse encontrar dois números inteiros positivos quadrados perfeitos cuja soma fosse um
quadrado perfeito, usaríamos o teorema de Pitágoras:
32 + 42 = 52 .
Agora, vamos ver que esta situação mais simples nos revela uma saída par o problema mais complexo. De
fato, multiplique cada lado da última igualdade por 52 , obtendo
32 .52 + 42 .52 = 52 .52
e substitua 52 na primeira parcela do lado esquerdo por 32 + 42 . Assim, obtemos
32 (32 + 42 ) + 42× 52 = 52 ⇐⇒ 32 .32 + 32 .42 + 42 .52 = 52 .52 .
Novamente, multiplicando cada lado da última igualdade por 52 , obtemos
32 .32 .52 + 32 .42 .52 + 42 .52 .52 = 52 .52 .52
e usando na primeira parcela à esquerda a substituição de 52 por 32 + 42 , obtemos:
32 .32 .32 + 32 .32 .42 + 32 .42 .52 + 42 .52 .52 = 52 .52 .52 .
Continuando esse processo, encontraremos 2014 números inteiros positivos distintos, que são quadrados
perfeitos, tal que a soma seja também um quadrado perfeito.
2.3
Experimente, procure algo que seja invariante
Muita matemática foi feita por tentativa, errando, corrigindo, aperfeiçoando, avançando.
As vezes pode ser vantajoso introduzir no problema algo novo, um auxílio extra, para que facilite você na
percepção entre o que foi dado e o que foi pedido.
2.3.1
Aplicação 2
Problema 2.3.1 - Tem-se quarenta e três pedaços de palitos, cujos comprimentos são 1, 2, 3, · · · , 42, 43
centímetros, respectivamente.
Diga, justificando, se é possível formar um quadrado usando todos estes pedaços, sem quebrar qualquer um
deles, nem sobrepor dois ou mais deles.
E se em vez de um quadrado for um retângulo?
Solução
Aqui é conveniente observar que
1 + 2 + 3 + · · · + 42 + 43 =
43 × (43 + 1)
= 43 × 22 = 946.
2
Se fosse possível formar um quadrado, de lado medindo x, usando todos estes pedaços, sem quebrar qualquer
um deles, nem sobrepor dois ou mais deles, teríamos necessariamente que o perímetro do quadrado seria
igual a 946. Ou seja, 4x = 946, o que é impossível, pois x tem de ser um número inteiro e o número 946 não
2.3 Experimente, procure algo que seja invariante
11
é divisível por 4.
Se em vez de um quadrado for um retângulo, com lados medindo a e b centímetros, teríamos o perímetro
do retângulo como sendo igual a 2a + 2b = 946, ou seja a + b = 473. Neste caso, a resposta é sim. Se os
quatro lados do retângulo medem a, a, b, b, poderíamos tomar:
a = 1 + 2;
e
a = 3, e
b = (4 + 43) + (6 + 41) + (8 + 39) + (10 + 37) + · · · + (19 + 29) + (20 + 27) + (22 + 25)
e
b = (5 + 42) + (7 + 40) + (9 + 38) + (11 + 36) + · · · + (19 + 28) + (21 + 26) + (23 + 24).
Problema 2.3.2 - Um tabuleiro 10 × 10 pode ser coberto por 25 dominós de dimensões 1 × 4?
Solução
Aqui o invariante mais óbvio é a área, que infelizmente não ajuda na solução do problema. Por outro
lado, podemos escrever um número em cada um dos 100 quadrados unitários do tabuleiro com a propriedade
que, não importa como nós colocamos um dos dominós cobrindo 4 quadrados, a soma dos números em
quatro quadrados coberto seja igual a zero; no entanto, a soma de todos os 100 números em todo o tabuleiro
não é zero. Então, obviamente, a cobertura é impossível.
Como associar os números aos quadrados unitários do tabuleiro do modo com prevemos acima?
Defina os valores an , para n = 1, 2, 3, · · · , 9, 10, da seguinte maneira:
a1 = 1
a2 = 1
a3 = 1
a4 = −3
a5 = 1
a6 = 1
a7 = 1
a8 = −3 a9 = 1
a10 = 1
Nesta sequência, qualquer bloco consecutivo de quatro termos tem soma igual a 0, mas a soma de todos os
dez não é 0. Agora, escrevemos no quadrado unitário do tabuleiro que está na linha m e coluna n o número
am × an , que nos sugere uma pintura para o tabuleiro usando três cores distintas, veja figura a seguir.
Problema 2.3.3 - (AUMO - 1978) Três máquinas caça-níqueis imprimem pares de inteiros positivos em
cartões. As máquinas caça-níqueis trabalham da seguinte maneira. A primeira máquina caça-níquel depois
de ler um cartão (a, b) imprime um novo cartão (a + 1, b + 1); a segunda máquina caça níquel depois de
ler um cartão (a, b) imprime um novo cartão ( a2 , 2b ). Esta máquina só funciona se os números a e b forem
pares. A terceira máquina caça-níquel, depois de ler dois cartões (a, b) e (b, c) imprime um novo cartão
(a, c). Além disso, as máquina caça-níquel devolvem todos os cartões lidos.
É possível começar com um cartão (4, 18) e chegar num cartão (1, 100)?
Solução
A resposta é não.
Para qualquer cartão (a, b) chame D(a, b) a diferença a − b. Seja S a coleção de todos os cartões obtidos a
partir do cartão (4, 18) por meio de operações consecutivas das máquinas caça-niquel.
Vamos mostrar que D(a, b) é divisível por 7, para cada (a, b) ∈ S. Isto é, o resto da divisão de D(a, b) por 7
é um invariante.
Para mostrar isso, vamos usar indução sobre o número de sucessivos usos das máquinas.
Observe que D(4, 18) = 4−18 = −14. Logo, o resto da divisão de D(4, 18) por 7 é zero: −14 = (−2)×7+0.
Vamos supor que depois do n−ésimo uso das máquinas tenhamos um cartão (a, b), com o resto da divisão
de D(a, b) por 7 igual a zero.
Vamos considerar o (n + 1)−ésimo uso das máquinas caça-niquel. Existem três casos possíveis:
• Usando a primeira máquina, depois de colocar o cartão (a, b), obtemos o cartão (a + 1, b + 1). Neste
caso, D(a + 1, b + 1) = (a + 1) − (b + 1) = a − b, que, por hipótese de indução, é divisível por 7;
• Usando a segunda máquina, depois de colocar o cartão (a, b), obtemos o cartão ( a2 , b2 ). Neste caso,
D( 2a , 2b ) = a2 − b2 ) = 12 (a − b), que, por hipótese de indução, é divisível por 7.
• Usando a terceira máquina, depois de colocar os cartões (a, b) e (c, d), obtemos o cartão (a, c). Neste
caso, D(a, c) = a − c = a − b + b − c = (a − b) + (b − c), que, por hipótese de indução, é divisível por
7, por ser soma de dois números múltiplos de 7.
12
Capítulo 2. ESTRATÉGIAS
Assim, em todos os três casos, o resto da divisão de D(a, b) por 7 no novo cartão é nulo. O mesmo é
verdade para o caso do cartão obtido a partir de (4, 18) nas três máquinas caça-niquel. Mas, D(1, 100) =
1 − 100 = −99 = (−15) × 7 + 6. Portanto, D(1, 100) deixa resto 6 na divisão por 7, consequentemente não
é possivel obter o cartão (1, 100) a partir do cartão (4, 18).
2.4
Faça um desenho e, dependendo da situação, pinte às cores.
Muitos de nós pensamos melhor com um desenho, esquema, imagem, do que com palavras. Diz o ditado
popular: uma imagem vale mais do que mil palavras.
Logo, sempre que puder, faça um esquema auxiliar, um desenho, pinte às cores. Essas atitudes, quase sempre
revelam caminhos surpreendentemente elegantes e fáceis de comprovar.
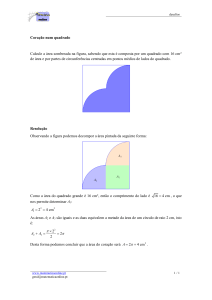
Problema 2.4.1 - Considere um tabuleiro de xadrez 8 × 8 e 32 dominós de dimensão 2 × 1. Os dominós
podem ser arranjados sobre o tabuleiro de modo a cobri-lo inteiramente, cada dominó cobrindo perfeitamente
dois quadrados unitários. Dois quadrados unitários, situados nos cantos do tabuleiro, são retirados, veja
Figura a seguir.
Diga, justificando, se 31 dominós cobrem completamente o tabuleiro reduzido.
Solução
A resposta é não.
A idéia aqui é pintar o tabuleiros de modo que as casas fiquem alternadamente pretas e brancas, veja figura
a seguir.
Observe que os dois quadrados situados nos cantos do tabuleiro possuem a mesma cor e que cada dominó
por inteiro cobre sempre uma casa de cada cor, independente de como você o coloca sobre o tabuleiro na
horizontal ou vertical. Assim, se a cobertura fosse possível deveríamos ter no tabuleiro a mesma quantidade
de casas de cada cor, o que não ocorre com a retirada de duas casas de mesma cor.
Portanto, 31 dominós não cobrirão completamente o tabuleiro reduzido.
Problema 2.4.2 - O rei, peça do jogo de xadrez, se movimenta uma única casa em todas as direções. Pode
o rei, começando do quadrado mais abaixo, à esquerda, ir até o quadrado mais acima à direita, visitando
cada uma das casas restantes do tabuleiro exatamente uma única vez?
2.4 Faça um desenho e, dependendo da situação, pinte às cores.
13
Solução
A resposta é não.
Pinte as casas do tabuleiro alternadamente pretas e brancas. Agora, basta observar que o rei vai de uma
casa de uma cor para a casa de cor oposta. omo o rei tem que fazer 63 movimentos, o último irá deixá-lo
em uma casa da cor oposta a cor da primeira casa. Mas, a priemira casa e a última possuem a mesma cor,
o que é uma contradição. Portanto, o rei não pode, começando do quadrado mais abaixo, à esquerda, ir
até o quadrado mais acima à direita, visitando cada uma das casas restantes do tabuleiro exatamente uma
única vez.
Problema 2.4.3 - Bolas de tênis de mesmo raio r são hermeticamente embaladas em latas cilíndricas com 3
bolas, onde elas apenas tocam a lata na superfície lateral, no topo e no fundo.
Qual é maior: a altura da lata embalagem ou a medida da circunferência de cada bola?
Solução
A resposta é: a medida da circunferência de cada bola.
Façamos um desenho da situação.
Observe que a altura da lata é igual a 3d, onde d é o diâmetro da circunferência de cada bola. A medida da
circunferência de cada bola é igual 2πr = 2π d2 = πd > 3d, pois π = 3, 14 · · · > 3.
Problema 2.4.4 - (BW - 2003) Diga, justificando, se é possível escolher 1000 pontos do plano de tal modo
que no mínimo 6000 distâncias entre dois deles sejam iguais.
Solução
A resposta é sim.
Comece com uma configuração de 4 pontos e 5 distâncias, veja figura a seguir.
Agora tome a figura acima e mais duas cópias congruentes a ela, obtidas por movimentos paralelos (e não
coincidentes), veja figuta a seguir.
Neste caso, tem-se 3 × 4 = 12 pontos e 3 × 5 + 12 = 27 distâncias. Agora junte mais três cópias da figura
acima, obtendo:
3 × 12 = 36 pontos e 3 × 27 + 36 = 117 dist âncias.
Agora, forme uma figura com 9 figuras congruentes a figura inicial, obtidas dela por movimentos paralelos
(e não coincidentes). Desse modo, temos
3 × 36 = 108 pontos e 3 × 117 + 108 = 459 dist âncias.
Procedendo desta maneira, sempre juntando mais 3 cópias da figura inicial, vamos obtendo gradativamente:
3 × 108 = 324 pontos e 3 × 459 + 324 = 1701 dist âncias.
3 × 324 = 972 pontos e 3 × 1701 + 972 = 6075 dist âncias.
Problema 2.4.5 - Numa sala quadrada de dimensões 13 × 13 retira-se o quadrado unitário central.
É possível ladrilhar o restante da sala usando ladrilhos retangulares de dimensões 1 × 4 ou 4 × 1?
Solução
Não.
Pinte os quadrados do assoalho de preto e branco no padrão seguinte. Na primeira linha acima, pinte de
preto os dois quadrados mais à esquerdal, pinte de branco os dois seguintes (da esquerda para direita), os
dois próximos pinte de preto, os dois próximos de branco, e assim por diante, de modo que na extremidade
direita fique um único quadrado preto. Na segunda linha, pinte a linha de forma alternada com a pintura da
primeira linha: dois quadrados brancos, dois quadrados pretos e assim por diante. Numerando as linhas de
1 a 13, temos que todas as linhas ímpar são pintadas de forma idêntica que a pintura da primeira linha e
todas as linhas numeradas com números pares são pintadas de forma idêntica que a pintura da linha de
número 2, veja figura a seguir.
Capítulo 2. ESTRATÉGIAS
14
Observe que existem mais quadrados unitários pretos do que quadrados brancos. Por outro lado, cada
ladrilho 4 × 1, não importa como seja colocado, cobre precisamente dois quadrados unitários pretos e dois
brancos. Assim, se um ladrilhamento deixar um único quadrado descoberto, este quadrado tem de ser preto.
Mas, o quadrado central é branco. Portanto, tal ladrilhamento é impossível.
2.5
2.5.1
Modifique o enunciado, para ver se lhe ocorre um caminho possível
Aplicação 3
Quando o problema parecer difícil demais, modifique o enunciado, transforme o problema em outro, isto
pode levar a um caminho que lhe mostre a saída.
Problema 2.5.1 - Calcule o valor da expressão E = (tan 15o ).(tan 30o ).(tan 45o ).(tan 60o ).(tan 75o ).
Solução
A idéia aqui é óbservar que se x + y = 90o , então
tan (x + y) =
tan x + tan y
= tan 90o = ∞.
1 − tan x. tan y
Ou seja, 1 − tan x. tan y = 0, que é o mesmo que tan x. tan y = 1, ou ainda
tan x =
1
1
=
= cot (90o − x)
tan y tan (90o − x)
Logo, temos que
tan 75o = cot (90o − 75o ) = cot 15o ;
tan 60o = cot (90o − 60o ) = cot 30o .
Portanto,
E = (tan 15o ).(tan 30o ).(tan 45o ).(tan 60o ).(tan 75o ) =
= (tan 15o ).(cot 15o ).(tan 30o ).(cot 30o ).(tan 45o ) = 1.1.1 = 1.
Problema 2.5.2 - (BW 2004) Escreve-se em cada uma das seis faces de um cubo um número inteiro positivo.
Para cada vértice do cubo, calcula-se o produto dos números nas três faces adjacentes a ele. A soma desses
produtos é igual a 1001
Qual é a soma dos seis números escritos nas faces do cubo?
Solução
Em vez de tomar aleatoriamente os seis números escritos nas faces do cubo, vamos considerar os
números dois a dois, escritos nas faces opostas. Assim, sejam a1 , a2 , b1 , b2 , c1 , c2 os números escritos nas
2.5 Modifique o enunciado, para ver se lhe ocorre um caminho possível
15
faces dos cubos de tal maneira que a1 , a2 estão escritos em faces opostas, b1 , b2 números ecritos em faces
opostas e c1 , c2 números escritos em faces opostas. Agora, a soma dos oito produtos:
a1 .a2 + a1 .b1 + a1 .b2 + a1 .c1 + · · · + c1 .c2 = 1001.
Por outro lado,
a1 .a2 + a1 .b1 + a1 .b2 + a1 .c1 + · · · + c1 .c2 = (a1 + a2 ).(b1 + b2 ).(c1 + c2 ) =
= 1001 = 7.11.13
. Portanto, a soma dos oito números escritos nas faces do cubo é igual a:
(a1 + a2 ) + (b1 + b2 ) + (c1 + c2 ) = 7 + 11 + 13 = 31.
Problema 2.5.3 - (BW 2001) Pintam-se ou de vermelho ou de verde 2001 pontos distintos sobre um círculo.
Em cada etapa, todos os pontos são simultaneamente pintados novamente da maneira seguinte:
se dois pontos são vizinhos imediatos de um ponto P e possuem a mesma cor que P, então a cor de P não se
altera, caso contrário P muda de cor.
Começando com a primeira pintura F1 , obtemos as pinturas F2 , f3 , · · · , depois de aplicar várias etapas de
pinturas.
Prove que existe um número n0 ≤ 1000 tal que Fn0 = Fn0 +2 . Isto é verdade se o número 1000 for substituído
pelo número 999?
Solução
A resposta é não.
Vamos denotar os pontos sobre o círculo por 1, 2, 3, · · · , 2001, de tal modo que os pontos i, j sejam vizinhos
se |i − j| = 1 ou {i, j} = {1, 2001}.
Vamos dizer que k pontos formam um segmento monocromático de comprimento k se os pontos são consecutivos sobre o círculo e se eles possuem a mesma cor.
Para uma pintura F, chamamos de d(F) o comprimento máximo de um segmento monocromático. Observe
que d(F) > 1, para todo n, pois 2001 é ímpar. Se d(F) = 2001, então todos os pontos possuem a mesma cor,
portanto, F1 = F2 = F3 = · · · e, neste caso, podemos escolher n0 = 1.
Seja 1 < d(F1 ) < 2001. Valem as seguintes propriedades:
(i) Se 3 < d(Fn ) < 2001, então d(Fn+1 ) = d(Fn ) − 2;
(ii)Se d(Fn ) = 3, então d( fn+1 ) = 2;
(iii) Se d(Fn ) = 2, então d(Fn+1)=d(Fn e fn+2 = fn ;
Se valem as três propriedades acima, segue de (i) e (ii) que d(F1000 ) ≤ 2 e por (iii) temos que F1000 = F1002 .
Além disso, se F1 é a pintura onde 1 é pintado de vermelho e todos os outros pontos são pintados de verde,
então d(F1 ) = 2000 e então d(F1 ) > d(F2 ) > · · · > d(F1000 ) = 2, o que mostra que para todo n < 1000,
temos Fn 6= Fn+2 e então 1000 não pode ser substituído por 999.
Agora, vamos provar as três propriedades acima.
Seja (i + 1, i + 2, , · · · , i + k) o maior segmento monocromático para Fn , considerando os pontos módulo 2001.
Então (i + 2, i + 3, · · · , i + k − 1) é um segmento monocromático para Fn+1 e segue que d(Fn+1 ) ≥ d(Fn)−2 .
Além disso, se (i + 1, i + 2, , · · · , i + k) é o maior segmento monocromático para Fn+1 , com k ≥ 3, então
(i, i + 1, · · · , i + k + 1) é um segmento monocromático para Fn . Disso, e do fato de Fn+1 > 1, seguem (i) e (ii).
Para provar (iii) observe que se d(Fn ) ≤ 2, então Fn+1 é obtido de Fn mudando as cores de todos os
pontos, o que conclui a prova.
Explore a simetria
Muitos problemas são resolvidos quando se explora a simetria que o problema apresenta, de forma explícita
ou mesmo mascarada.
Aplicação 4
Problema 2.5.4 - Inscreve-se um quadrado num círculo, que por sua vez está inscrito noutro quadrado, veja
figura a seguir.
Capítulo 2. ESTRATÉGIAS
16
Qual é a razão das áreas dos dois quadrados?
Solução
Podemos resolver o problema usando a noção de simetria. Se você gira o quadrado menor por um
ângulo de 450 , seus vértices irão coincidir com os pontos de tangência do círculo e do quadrado maior.
Portanto, é fácil ver, que o quadrado menor possui a metade da área do quadrado maior.
Problema 2.5.5 - (CMO 1978) Eve e Odette disputam um jogo num tabuleiro 3 × 3, com peças brancas e
peças pretas. As regras são as seguntes:
I - Elas jogam alternadamente;
II - Uma jogada consiste em colocar uma peça numa casa do tabuleiro ainda não ocupadada
III - Na sua vez de jogar, uma jogadora pode escolher ou uma peça branca ou uma peça preta e não precisa
usar sempre a mesma cor;
IV - Quando o tabuleiro está totalmente preenchido pelas peças, Eves obtém um ponto para toda linha,
coluna ou diagonal que possuir um número par de peças pretas, e Odette obtém um ponto para toda linha,
coluna ou diagonal que possuir um número ímpar de peças pretas;
V - A jogadora que obtiver no mínimo cinco dos oito pontos VENCE.
Descreva uma estratégia vencedora para a garota que começa o jogo.
Solução
Vamos supor que Eve começa o jogo.
Eve coloca uma peça preta na casa central do tabuleiro, ela existe pois no tabuleiro temos 9 casas. A partir
daí, sempre que Odette jogar, Eve joga com uma peça da cor oposta a de Odette na casa simétrica, em
relação a casa central, daquela que Odette jogou. Por este procedimento, Eve obtém um ponto para toda
linha, coluna e diagonal que passem pelo centro. Além disso, pelo menos uma das linhas ou colunas que
passam pelo centro tem 2 peças pretas, daí Eves vence o jogo.
Chamando de B uma peça branca e P uma peça preta, no fianl do jogo o tabuleiro terá a seguinte aparência:
P
P
1
P
2
B
B
Exatamente um das casas 1 e 2 possui uma peça preta, e a linha dela possui um número par de peças pretas.
2.6
Redução ao Absurdo.
Um raciocínio muito empregado na resolução de problemas é aquele que comumente se chama de método
por redução ao absurdo ou método indireto.
Como é que funciona?
Se você pretende mostrar que uma afirmação A implica numa afirmação B, comece supondo que isto não
acontece. Ou seja, que A não implica em B. Fazendo deduções e raciocínios corretos, você chegará à
conclusão de que uma afirmação, que você sabe que é correta, não se realiza. Ou seja, você chegará a uma
contradição. Portanto, A implica em B.
Problema 2.6.1 - Demonstrar que o número
√
2 é irracional.
Solução
√
√
Suponha o contrário. Isto é, 2 não é um número irracional. Isto significa dizer que 2 = mn , onde
m, n ∈ Z, com n 6= 0. Sem perda de generalidade, vamos supor que os números m e n sejam relativamente
√
2
primo. Ou seja, MDC(m, n) = 1. Elevando ao quadrado ambos os membros de 2 = mn , obtemos 2 = mn2 ,
que é o mesmo que dizer que
m2 = 2n2
(∗).
Assim, m2 é par e, logo, m é par. Desse modo, m = 2k, onde k ∈ Z. Substituindo esse valor de m em (*),
obtemos que n2 é par, o que implica que n é par. Assim, concluímos que m é par e n é par. Uma contradição,
2.7 Suponha o problema resolvido (ou olhe de trás para diante)
pois tínhamos suposto MDC(m, n). = 1. Portanto, o número
17
√
2 é irracional.
Problema 2.6.2 - (BW - 2001) Escrevem-se os números 1, 2, 3, · · · , 49 nas casas de um tabuleiro 7 × 7,
sendo um número em cada casa e calcula-se a soma dos números em cada linha e cada coluna. Algumas
dessas 14 somas são ímpares enquanto as outras são pares. Seja A a soma de todas as somas ímpares e B a
soma de todas as somas pares.
É possível colocar os números nas casas do tabuleiro de modo que A = B?
Solução
A resposta é não.
Se isto fosse possível, teríamos 2 × (1 + 2 + 3 + 4 + · · · + 49) = A + B = 2B. Mas, B é um número par, pois
é a soma de números pares. Por outro lado, 1 + 2 + 3 + 4 + · · · + 49 = 25 × 49, que é um número ímpar.
Contradição. Portanto é impossível colocar os números nas casas do tabuleiro de modo que A = B.
Problema 2.6.3 - (TT - 1984) temos 2000 maçãs em várias bolsas. Podemos remover bolsas e/ou remover
maçãs das bolsas.
Prove que é possível ter um número igual de maçãs em cada uma das bolsas restantes, sendo o total de maçãs
não menor do que 100.
Solução
Suponha o contrário. Assim, o número total de bolsas restantes não é mais do que 99, caso contrário,
poderíamos deixar 1 maçã em cada uma das 100 bolsas e remover as restantes. Além disso, o total de bolsas
com no mínimo duas maçãs não é mais do que 49, o total de bolsas com no mínimo três maçãs não é mais
do que 33, etc. Portanto, o total de maçãs não é maior do que 99 + 49 + 33 + · · · . Existem 94 termos depois
dos cinco primeiros termos , cada um deles sendo menor do que ou igual a 16. Agora
99 + 49 + 33 + 24 + 19 + 94 × 16 = 1728 < 2000.
Contradição. Portanto, é possível ter um número igual de maçãs em cada uma das bolsas restantes, sendo o
total de maçãs não menor do que 100.
Problema 2.6.4 - (KMO- 1981) Seja p um número primo, p > 3. Sabe-se que para um certo inteiro positivo
n o número pn possui 20 dígitos, quando escrito na base 10.
Prove que dentre esses dígitos existem no mínimo três iguais.
Solução
Suponha o contrário. Isto é, dentre os 20 dígitos do número pn não existem três iguais. Isto significa que
um dos dígitos 0, 1, 2, 3 · · · , 9 é usado na representação decimal de pn exatamente duas vezes. Assim, a soma
dos dígitos de pn é igual a
2 × (0 + 1 + 2 + · · · + 9) = 90.
Logo, pn é divisível por 3. Mas, isso é uma contradição, pois p é um primo maior do que 3, o que implica
que pn não pode ser divisível por 3. Portanto, dentre es dígitos de pn existem no mínimo três iguais.
2.7
Suponha o problema resolvido (ou olhe de trás para diante)
Uma tática que pode ser utilizada em jogos ou problemas em que se tem de construir alguma figura, é supor
o problema resolvido. Então você poderá reverter seus passos e, portanto, construir uma solução para o
problema original.
2.7.1
Aplicação 4
Problema 2.7.1 - Dois amigos, A e B se divertem com o seguinte jogo, em que jogam alternadamente. O
primeiro a jogar, A, escolhe um inteiro qualquer de 1 a 11, inclusive, e comunica ao segundo jogador, B, a
sua escolha e este soma-o à qualquer número de 1 a 11, inclusive, por ele escolhido, falando o resultado ao
primeiro jogador, que o soma à qualquer número escolhido de 1 a 11, e assim eles vão jogando, alternadamente, até que um deles obtenha o número 56, vencendo o jogo.
Capítulo 2. ESTRATÉGIAS
18
Quem vence: A ou B? Qual é a estratégia para vencer?
Solução
O jogador A, que começa, vence.
Na sua penúltima jogada, o jogador A tem de deixar para B uma soma menor do que 56 − 11 = 45, para
garantir que B não possa atingir o número 56. Assim, ele deixa a soma igual a 44. Na sua jogada
imediatamente anterior ele deixa para o jogador B uma soma menor do que 44 − 11 = 33, para garantir
que o jogador B não possa atingir 44. Desse modo, as jogadas vencedoras de A são de tal maneira que os
totais atingidos por eles sejam: 8, 20, 32, 44 e 56.
Problema 2.7.2 - Dois amigos, A e B, disputam seguinte jogo, em que jogam alternadamente, usando um
monte com 27 de caroços de feijão. O jogador A começa. Uma jogada consiste em retirar 1, 2, 3 ou 4 caroços
do monte. O jogo termina quando todos caroços forem removidos. O vencedor é aquele que possuir um
número par de caroços quando todos os caroços tiverem sido retirados.
Quem vence: A ou B? Qual a estratégia vencedora?
Solução
(Solução por David Angell, University of New South Wales, Australia. Fonte: [1]
Descreva a posição do jogo num momento qualquer por um par:
• (n, I), se existem no monte n caroços de feijão e se o jogador que vai fazer seu movimento possui um
número ímpar de caroços ou
• (n, P) se existem no monte n caroços de feijão e se o jogador que vai fazer seu movimento possui um
número par de caroços.
Dizemos que uma posição é uma posição vencedora se o jogador que tem a vez de jogar pode garantir que
vai vencer, não importando como o outro jogue. Assim, temos:
• (1, I) é uma posição vencedora, porque o jogador que vai fazer seu movimento retira o último caroço
e fica com um número par deles.
• (1, P) é uma posição perdedora, pois o jogador que vai fazer seu movimento retira o último caroço e
fica com um número ímpar deles.
• (2, I) é uma posição vencedora, porque retirando um caroço fica com um número par deles e deixa o
oponente na posição (1,P), que é uma posição perdedora..
• (2, P) é uma posição vencedora, pois o jogador que vai fazer seu movimento retira os dois últimos
caroços e termina com um número par deles.
• Por razões análogas, (3, I), (3, P), (4, I) e (4, P) são posições vencedoras. Por exemplo, na posição
(3,P) o oponente possui um número par de caroços, retirando dois caroços coloca o oponente na
posição (1, P), que, como vimos acima, é uma posição perdedora.
• (5, I) é uma posição perdedora, pois o oponente possui um número ímpar de caroços, pois qualquer
movimento deixa-o em uma das posições (4, I) ou (3, I) ou (2, I) ou (1, I).
• (5, P) é uma posição vencedora, porque retirando 4 caroços coloca o oponente na posição perdedora
(1, P).
• (6, I) é uma posição perdedora porque o oponente possui um número par de caroços, e qualquer
movimento leva-o para uma das posições vencedoras (5, P) ou (4, P) ou (3, P) ou (2, P).
• (6, P) é uma posição vencedora, pois retirando 1 caroço coloca o oponente na posição perdedora
(5, I). Se você continuar com esse raciocínio, vai descobrir que agora a situação se repete: as posições
vencedoras e perdedoras para n caroços são as mesmas que para n − 6 caroços. Por exemplo, se
n = 7, então (n, I) vence e (n, P) perde, mesmo para n = 1; se n = 8, então ambas as posições (n, I) e
(n, P) vencem; o mesmo para n = 2, e assim por diante.
Portanto, para n = 27, começando com um número par de caroços (0 é um número par) é essencialmente o
mesmo que a posição (3, P) e o primeiro jogador vence retirando dois caroços.
A estratégia vencedora é simplesmente seguir a tabela de instruções dada abaixo. Como existem realmente
somente doze posições de (1, I) a (6, P), e três delas são posições perdedoras, segue que não importa como
você jogue, existem nove posições vencedoras para memorizar. Essas posições vencedoras estão na tabela
abaixo, onde n (mod 6) significa o resto quando n é dividido por 6.
2.7 Suponha o problema resolvido (ou olhe de trás para diante)
n (mod 6)
0
1
n Impar nenhum
1(2)
n Par
1
nenhum
2
3
4
1
3(4) 3
2(3)
2
4
5
nenhum
4
19
3. Problemas Diversos
Problema 3.0.1 - (AMO) Começando com um hexágono regular, uma forma geométrica é gerada em
estágios. Na Fase 1, há um hexágono. Cercando-o completamente, adicionando um hexágono regular
congruente ao incial, para cada lado dele exposto, temos que na Fase 2, existem 7 hexágonos no total.
Cercando completamente a nova forma pela adição de um hexágono regular, congruentes aos outros, para
cada lado exposto, temos que na Fase 3 existem um total de 19 hexágonos, veja Figura a seguir.
Encontre uma fórmula para o número total de hexágono em Fase n.
Solução
No hexagono inicial, traçamos as três maiores diagonais e as prolongamos. Elas cortam a figura em 6
partes congruentes, veja Figura a seguir.
Agora, omitindo o hexágono central, observa-se que a quantidae de hexágono em cada parte congruente e
em cada estágio é:
1
1
1
1
1
1
+1+
, 3,
+3+
, 5,
+5+
, 7, · · ·
1,
2
2
2
2
2
2
Isto é, a quantidae de hexágono em cada parte congruente e em cada estágio é:
1, 2, 3, 4, 5, 6, 7, · · · , n − 1
(depois de n est ágios)
Portanto, se Tn é o número de hexágonos no estágio n, temos que
Tn = 6[1 + 2 + 3 + 4 + 5 + · · · + (n − 1)] + 1 =
6n(n − 1)
+ 1 = 3n(n − 1) + 1 = 3n2 − 3n + 1.
2
Problema 3.0.2 - (CM, 37: No 5 September 2011) Juliette e Philippe disputam um jogo em que fazem seus
movimentos alternadamente. No início do jogo, cada vértice de um quadrado é coberto por um número de
fichas. Um movimento consiste em cada jogador escolher um lado do quadrado e retirar de suas extremidades
tantas fichas quanto ele desejar, desde que ele retire pelo menos uma. Não é necessário retirar o mesmo
número de fichas de cada extremidade. O jogador que retirar a última ficha vence o jogo. No início do jogo,
existem 10 fichas no vértice A, 11 fichas no vértice B, 12 fichas no vértice C e 13 fichas no vértice D.
Se Juliette começa, qual é a sua estratégia para vencer?
22
Capítulo 3. Problemas Diversos
Solução
Sejam a, b, c e d o número de fichas nos vértices A, B,C e D, respectivamente. A estratégia de Juliette é
fazer seus movimentos para ter a = c e b = d.
Se na sua vez de jogar, Philippe recebe um quadrado com a = c e b = d, então ele retira no mínimo uma
ficha, e não pode retirar fichas de ambos os extremos de uma diagonal. Portanto, ele sempre passa para
Juliette um quadrado com a 6= c e b 6= d. Se Juliette recebe um quadrado a 6= c e b 6= d, então para cada
diagonal ela deve escolher a extremidade com maior número de fichas. Nesse caso, ela deve escolher o lado
que liga essas duas extremidades e retirar fichas até que a = c e b = d. Assim, ela sempre pode aplicar essa
estratégia e obter a = c = 0 e b = d, vencendo o jogo.
Problema 3.0.3 - (OMM - 2003) Tem-se cartões sobre uma mesa de modo que em cada um deles está
escrito um par de números inteiros positivos. Existe exatamente um cartão para cada par de números inteiros,
(a, b), com 1 ≤ a < b ≤ 2003. Dois jogadores disputam um jogo, em que jogam alternadamente. Cada
movimento corresponde a retirar um cartão e escrever no quadro-negro o produto ab dos números lá escritos.
O primeiro jogador que faz com que o Máximo Divisor Comum dos números no quadro-negro seja igual a
1 perde.
Qual dos jogadores tem uma estratégia vencedora: o primeiro ou o segundo a jogar?
Solução
O primeiro jogador tem uma estratégia vencedora.
Considere os números no quadro-negro imediatamente antes do movimento perdedor. O Máximo Divisor
Comum de todos esses números deve ser um inteiro d > 1.
Se d não é um número primo, então ele possui algum divisor, k, menor do que ele, de modo que o cartão
com o par (1, k) ainda pode ser retirado. Contradição, pois o próximo movimento é perdedor.
Logo, d é um número primo e todo cartão com um par (a, b), com d dividindo ab deve ter já sido retirado.
Existem 2002 pares da forma (a, d), pois, pela hipótese do problema, a pode ser qualquer um dos números
1, 2, 3, ..., 2003 exceto d. De maneira análoga, existem 2002 pares da forma (a, 2d), com 2d ≤ 2003. Agora,
observe que, deste modo, contamos duas vez o par (d, 2d). Logo, d tem de ser escolhido de modo que
2d < 2003 < 3d, o que implica que existem 4003 pares possíveis.
O primeiro jogador pode vencer se ele retira o par (1, 997). Assim, as possíveis jogadas são:
(k, 997), para k = 2, 3, 4, ..., 996, 998, ..., 2003 (que são 2001 possibilidades), e (k, 1994), para k =
1, 2, 3, ..., 996, 998, 999, ..., 1993, 1995, 1996, ..., 2003 (que são 2001 possibilidades).
Portanto, existe um número par de movimentos disponíveis e o primeiro jogador vencerá. Observe que o
segundo jogador só pode reduzir o número de movimentos disponíveis se ele perder.
Problema 3.0.4 - (HMITMT - 2003) Num hotel os quartos estão dispostos como um tabuleiro 2 × 8, estando cada um deles ocupado por umm hóspede. Todos os hóspedes estão se sentindo desconfortáveis em
seus aposentos, de modo que cada um deles gostaria de passar para um quarto adjacente, horizontal ou
verticalmente. Naturalmente, eles podem fazer a mudança simultaneamente, de tal maneira que cada quarto
fique novamente ocupado com um hóspede.
De quantas maneiras distintas podem ser feitos esses movimentos coletivos?
Solução
Imagine que os quartos são pintados alternadamente de preto e branco, no estilo de um tabuleiro de
xadrez, veja figura a seguir.
Pela figura, é fácil ver que, cada hóspede se movimenta de um quarto preto para um quarto adjacente branco,
e vice-versa. Se para um hóspede, que inicialmente está num quadrado preto, colocamos um dominó sobre
o quarto antigo e o novo, obtemos uma pintura do tabuleiro do tipo 2 × n, formada por n dominós, pois
cada quadrado preto é usado uma vez e cada quadrado branco é usado uma vez. Aplicando procedimento
análogo para cada hóspede que inicialmente está num quarto branco e se movimenta para um quadrado
preto, obtemos uma segunda pintura para o tabuleiro. Inversamente, é fácil verificar que, para qualquer par
de quadrados dessas pinturas, determina um padrão de movimento. Também é fácil provar por indução
que o número de pinturas do tipo dominós de um tabuleiro de dimensões 2 × n é (n + 1)-ésimo número de
23
Fibonacci.
Isto é fácil de ver para os casos de n = 1, 2 e para um retângulo 2 × n, onde os dois quadrados mais
a direita pertencem a um dominó vertical ou deixam um retângulo de dimensão 2 × (n − 1) ser pintado
arbitráriamente, ou dois dominós ocupam quadradados adjacentes, deixando um retângulo de dimensão
2 × (n − 2) ser pintado livremente. Portanto, o número de pinturas possíveis é o número de Fibonacci.
Deste modo, o número de pinturas de um tabuleiro de dimensão 2 × 8 é 34, e o número possível de pares de
tais pinturas é igual a 342 = 1156, que é a resposta ao problema.
Problema 3.0.5 - (HMITMT - 2002) Sem levar em consideração a ordem das parcelas, de quantas maneiras
podemos expressar 2002 como soma de 3 inteiros positivos?
(Consideramos 2 + 1000 + 1000 e 1000 + 2 + 1000 como sendo a mesma forma de expressar 2002 como
soma de 3 inteiros positivos)
Solução
Sejam a, b e c três números positivos para os quais a + b + c = 2002. Para facilitar o entendimento
e evitar redundancia, vamos supor que a ≤ b ≤ c. Observe que, para cada escolha de a e b, existe uma
única escolha para c, pois c = 2002 − (a + b). Agora, vamos contar todas as possibilidades para a e b
considerando dois casos:
Caso 1 O número a é par.
Caso 2 O número a é ímpar.
Suponha que o número a do terno procurado seja um número par. Neste caso, para cada valor de a, teríamos
b = c = 2002−a
, que é um número inteiro. Com isso, teríamos a + 2002−a
+ 2002−a
= 2002, satisfazendo ao
2
2
2
2002−a
problema. Observe que, para b = 2 ≥ a, segue que 2002 − a ≥ 2a, que é o mesmo que a ≤ 667. Como
a é um número par, temos 2 ≤ a ≤ 666.
Para cada valor de a, existem ( 2002−a
− a + 1) valores para b. Ou seja, para cada valor de a, existem
2
2002−a−2a+2
3a
= 1002 − 2 valores para b.
2
3×4
Agora, se a = 2, temos 1002 − 3×2
2 = 999 valores para b. Se a = 4, temos 2002 − 2 = 996 valores
3×6
para b. Se a = 6, temos 2002 − 2 = 993 valores para b, e assim por diante até a = 666, que nos dá
2002 − 3×666
= 3 valores para b. Para calcular a quantidade de todos os números a, b, c possíveis, quando a
2
é um número par, somamos os números obtidos anteriormente, que formam uma progressão aritmética. Isto
é, a quantidade de valores possíveis para os ternos de número a, b, c, com a par, satisfazendo ao problema é
igual a: 999 + 996 + 993 + ... + 3 = 999+3
2 × 333 = 501 × 333 = 166833.
Seja a um número ímpar. Neste caso, para cada valor de a, existem [ (2002−(a+1)
− a + 1] = [ (2002−a−1−2a+2
]
2
2
3(a−1)
2000−3(a−1)
] = 1000 − [ 2 ] possíveis valores para o número b.
=[
2
Como dado o número a, tem-se: b = 2002−(a+1)
≥ a, segue que 2002 − (a + 1) ≥ a, que é o mesmo que
2
a ≤ 667. Como a é um número ímpar positivo, temos 1 ≤ a ≤ 667.
Agora, se a = 1, temos que existem 1000 − 3×(1−1)
= 1000 valores possíveis para b. Se a = 3, existem
2
3×(3−1)
1000 − 2
= 997 valores possíveis para b. Se a = 5, existem 1000 − 3×(5−1)
= 994 valores possíveis
2
3×(667−1)
para b, e assim por diante até a = 667, que nos dá 1000 −
= 1 valor possível para b. Para
2
calcular a quantidade de todos os números a, b, c possíveis, quando a é um número ímpar, somamos
os números obtidos anteriormente, que formam uma progressão aritmética. Isto é, a quantidade de
valores possíveis para os ternos de número a, b, c, com a ímpar, satisfazendo ao problema é igual a:
× 334 = 1001 × 167 = 167167.
1000 + 997 + 994 + ... + 1 = (1000+1
2
Portanto, existem 166833 + 167167 = 334000 possíveis arranjos dos números inteiros positivos a, b, c
satisfazendo ao problema.
Problema 3.0.6 - (TT - 2012) Um tesouro está enterrado num tabuleiro de xadrez 8 × 8. Em cada uma das
casas do tabuleiro existe enterrado uma mensagem que indica o número mínimo de passos que se necessita
para chegar a casa do tesouro. Necessita-se de um passo para se mover de uma casa para a casa vizinha, que
é uma que tem um lado comum com a casa de partida.
Determine o número mínimo de casas que se deve escavar para chegar com certeza ao tesouro.
Solução
Se escolhemos uma casa qualquer para escavar, não há nenhuma garantia de que o tesouro esteja lá.
Se a mensagem retirada diz que o tesouro está num outro quadrado, não é possível determinar a exata
localização dele fazendo uma só escavação. Vamos provar que, para encontrar o tesouro, temos que escavar
24
Capítulo 3. Problemas Diversos
duas casas.
Numeramos as linhas do tabuleiro 8 × 8, de baixo para cima, de 1 a 8 e as colunas, da esquerda para a
direita, de 1 a 8. Assim, cada casa do tabuleiro é perfeitamente identificada por um par de números (b, c),
veja figura a seguir.
Escavamos as casas (1, 1) e (8, 1). Sejam a e b, respectivamente, os números que encontramos após
escavarmos as duas casas. Cada um desses números representa o comprimento do caminho mínimo que
devemos fazer da casa escavada até o tesouro. Podemos imaginar, sem perda de generalidade, que o caminho
mínimo realiza primeiro todos os movimentos verticais necessários em seguida e, após isso, os movimentos
horizontais até atingir o tesouro.
Vamos supor que o tesouro esteja na casa (i, j) do tabuleiro. Os caminhos mínimos para se atingir o tesouro,
a partir das casas escavadas, são de dois tipos:
Tipo (I) - aquele que começa na casa (1, 1), vai até a casa (1, j) e daí até a casa (i, j).
Tipo (II) - aquele que começa na casa (8, 1), vai até a casa (8, j) e daí até a casa (i, j).
Deste modo, sejam V1 e H1 a quantidade de movimentos verticais e horizontais, respectivamente, a partir da
casa (1, 1) até chegar ao tesouro e V2 e H2 a quantidade de movimentosos verticais e horizntias a partir da
casa
(8, 1) até chegar ao tesouro. Desse modo, temos que:
V1 + H1 = a
V2 + H2 = b
Pelo que indicamos acima, os movimentos horizontais dos dois caminhos são os mesmos, i. e. H1 = H2 , e a
diferença | a − b | é igual a diferença entre os comprimentos dos movimentos verticais dos dois caminhos.
Além disso, a soma dos comprimentos dos dois movimentos verticais é igual a V1 +V2 = 7.
Portanto,
supondo a ≥ b, teremos um sistema de equações lineares 2 × 2:
V1 −V2 = a − b
.
V1 +V2 = b
Este sistema tem solução única, o que determina exatamente a posição do tesouro.
Para ilustrar, considere o tabuleiro a seguir com o número obtido com a escavação em cada casa e o local
do tesouro.
Quando escavamos a casa (1, 1) obtemos o número a = 9. Isto é, o caminho mínimo de (1, 1) até o tesouro
tem comprimento 9. Quando escavamos a casa (8, 1) obtemos o número b = 8. Ou seja, o caminho mínimo
de (8, 1) até o tesouro tem comprimento 8.
Para se mover da casa (1, 1) até o tesouro, casa (5, 6), temos que fazer um movimento vertical até a
casa (5, 1) e de lá fazemos um movimento horizontal até a casa (5, 6). Além disso, a diferença 9 − 8 = 1.
Logo, temos que encontrar dois números cuja soma seja 7 e cuja diferença seja 1. Os únicos números
que satisfazem são 3 e 4. Portanto, de (1, 1) temos que descer 3 casas e, de (8, 1), mover para cima 4
casas. Como o comprimento do caminho mínimo de (1, 1) até o tesouro é 9, temos que andar 5 casas
horizontalmente. Portanto, o tesouro está na casa (5, 6).
Problema 3.0.7 - (LMO - 1987) Num tabuleiro 8 × 8 comum, com as casas pintadas alternadamente de
preto e branco, um movimento permitido é trocar de posição quaisquer duas linhas ou colunas.
Aplicando uma sequência de tais movimentos, é possível obter um tabuleiro onde a metade à esquerda seja
totalmente formada por casas pretas e a metade à direita seja formada inteiramente por casas brancas?
Solução
Observe que, em qualquer movimento permitido, não se altera o número de quadrados pretos numa
coluna do tabuleiro, que inicialmente é quatro. Logo, nunca obteremos uma coluna consistindo de oito
quadrados pretos. Portanto, é impossível obter um tabuleiro onde a metade à esquerda seja totalmente
formada por casas pretas e a metade à direita seja formada inteiramente por casas brancas.
Problema 3.0.8 - (OIM - 2000) Um mágico tem cem cartões numerados de 1 a 100. Ele coloca os cartões
em três caixas, uma vermelha, uma branca, uma azul, de tal modo que cada caixa contém no mínimo um
cartão. Uma pessoa da platéia escolhe duas dessas caixas e retira cartões de cada uma delas. Em seguida,
revela a soma dos números daqueles cartões. Dada esta informação, o mágico localiza a caixa da qual
nenhum cartão foi retirado.
25
De quantas maneiras o mágico pode repartir os cartões nas caixas de modo que ele possa sempre executar
seu truqie com êxito?
(Duas maneiras de repartir os cartões são consideradas distintas se ao menos um cartão é colocado em duas
caixas diferentes)
Solução
A resposta é 12.
Vamos chamar, respectivamente, de r, w, b as cores das caixas vermelha, branca, azul.
Vamos dizer que a cor do número i seja a da cor da caixa em que ele se encontra e todo número considerado
esteja no conjunto {1, 2, 3, · · · , 100}.
Para que o truque funcione, sempre que x + y = z +t e os cartões de números x e y estejam em casas distintas,
então ou z e t estão nestas mesmas caixas ou ambos estão na caixa restante. Isso significa dizaer que,
nenhum par de número de cores distintas tem a mesma soma que outros dois em caixas distintas.
Consideramos dois casos:
Caso 1: Suponhamos que existe uma caixa tal que os cartões numerados com i, i + 1, i + 2 são de cores
distintas, digamos vermelho (r), branco (w), azul (b), respectivamente.
Questão: Em que caixa está o cartão de número i + 3?
Está na caixa vermelha. De fato, como |{z}
i + (i + 3) = (i + 1) + (i + 2), para que o truque funcione, (i + 3)
| {z } | {z } | {z }
r
w
?
b
tem de ser vermelho (r).
De modo análogo, como (i + 4) + (i + 1) = (i + 3) + (i + 2), para que o truque funcione, segue que (i + 4) é
| {z } | {z } | {z } | {z }
w
?
r
b
branco (w). Do mesmo modo, como (i − 1) + (i + 2) = (i) + (i + 1), segue que (i − 1) é branco (w)
| {z } | {z } |{z} | {z }
?
r
b
w
Com isso, concluímos que três cores vizinha distintas determinam a cor do próximo número. Além disso,
este processo se repete: rwb é seguido por r, w, b e assim por diante. Este processo também funciona
inversamente: rwb é precedido por b, e assim por diante.
Logo, é suficiente definir as cores dos cartões numerados com 1, 2, 3, que pode ser feito de 6 modos distintos. Todos esses arranjos são tais que as somas dos números vermelhos e azuis, dos números brancos e
azuis, e dos números vermelhos e azuis, são restos distintos módulo 3. Isto é, a primeira caixa comtém os
cartõe de números 1, 4, 7, · · · , 100, a segunda caixa contém os de números 2, 5, 8, · · · , 98 e a terceira contém
3, 6, 9, · · · , 99
Caso 2: Suponhamos que não existem três cartões com números consecutivos em caixas distintas. Sem perda
de generalidade, suponhamos que o número 1 seja vermelho (r).
Agora, seja i o maior número que não é vermelho. Vamos supor que i seja branco. Seja k o menor número
azul. Como, por hipótese, não existe três números consecutivos de cores distintas, rwb, temos necessariamente que (i + 1) < k.
Suponhamos que k < 100. Como |{z}
i + |{z}
k = (i − 1) + (k + 1), segue que (k + 1) é vermelho (r). No
| {z } | {z }
w
b
r
?
entanto, como |{z}
i + (k + 1) = (i + 1) + |{z}
k , segue que (i + 1) deve ser azul b, o que contradiz o fato de
| {z } | {z }
w
r
?
b
que k é o menor número azul. Logo, k = 100.
Do mesmo modo, como (i − 1) + |{z}
100 = |{z}
i + |{z}
99 , segue que 99 é branco.
| {z }
r
b
w
?
Se t é um número inteiro, com t > 1 e o cartão numerado com t esteja na caixa vermelha (r), como
t + |{z}
99 = (t − 1) + |{z}
100 , temos que (t − 1) é azul (b), segue que o menor número azul é 100. Portanto,
|{z}
| {z }
r
w
?
b
a pintura dos números é feita do seguinte modo: rww · · · wwb.
Deste modo, se a soma é maior do que ou igual a 100, então a caixa restante é azul; se a soma é 101, a
caixa restante é branca; e se a soma é maior do que 101, a caixa restante é vermelha. Ou seja, uma caixa
contém o cartão com número 1, uma outra caixa contém os cartões com os números 2, 3, 4, · · · , 99 e a outra
caixa contém somente o cartão com número 100. O número de tais arranjos é 6.
Portanto, a resposta ao problema é 6 + 6 = 12.
Problema 3.0.9 - (OIM - 1986) Provar ou dê um contra-exemplo: Dado um conjunto finito de pontos no
26
Capítulo 3. Problemas Diversos
plano com coordenadas inteiras, é possível pintar de vermelho alguns destes pontos e os restantes de branco
de tal forma que para qualquer reta L paralela a um dos eixos coordenados, o número de pontos vermelhos e
o número de pontos brancos sobre L diferem por no máximo 1.
Solução
A resposta é sim.
Sejam P1 , P2 , P3 , · · · , Pn pontos sobre uma reta l paralela a um eixo, contados da esquerda para a direita e de
cima para baixo. Desenhamos segmentos juntando P1 a P2 , P3 a P4 , · · · . De um modo geral, traçamos um
segmento juntando os pontos P2i−1 a P2i . Feito isso para toda dessas retas l, obtemos uma algumas linhas
poligonais. Se uma dessas poligonais é fechada, significa que ela forma um poligono com um número par de
vértices. Agora, pintamos os vértices dessa poligonal alternadamente de vermelho e branco. Um ponto que
não esteja sobre a poligonal pode ser pintado de forma arbitrária. A pintura obtida satisfaz ao problema.
Problema 3.0.10 - (LMO - 1989) Dadas 32 pedras de pesos distintos, prove que 35 pesagens num balança
de dois pratos são suficiente para determinar quais são as duas pedras mais pesadas.
Solução
Inicialmente, dividimos as 32 pedras em 16 pares e, fazendo 16 pesagens, separamos o conjunto das
16 pedras mais pesadas. Agora, dividimos as 16 pedras mais pesadas em pares e, com 8 pesagens, determinamos as 8 mais pesadas dentre as 16 mais pesadas. Repetindo o processo, dividimos as 8 pedras mais
pesadas em pares e, com quatro pesagens, encontramos a 4 mais pesadas. Repetindo o processo, podemos
determinar a mais pesada das pedras depois de 16 + 8 + 4 + 2 + 1 = 31 pesagens.
Durante as pesagens, a segunda pedra com mais peso só poderia ser eliminada pela pedra mais pesada.
Nesse momento, você conhece a pedra mais pesada e as 6 mais pesadas. Agora, fique só com as 5 mais
pesadas. Extraia as 5 pedras que foram pesadas contra a pedra mais pesada durante as pesagens. Nesse
momento, é fácil de encontrar a mais pesado dessas 5 pedras em apenas 4 pesagens sucessivas, fazendo a
pesagem duas a duas e eliminando a mais leve.
Problema 3.0.11 - (SAMO - 1996) Um polígono convexo possui 2n lados. Prove que o polígono contém
no mínimo n diagonais que não são paralelas a qualquer um de seus lados.
Solução
= n(2n − 3) diagonais. Agora, observe que, para
Como o polígono possui 2n lados, ele possui 2n.(2n−3)
2
cada lado, existem no máximo (n − 2) diagonais paralelas a ele. Deste modo, existem no máximo 2n(n − 2)
diagonais paralelas a algum lado. Portanto, existem no mínimo n(2n − 3) − 2n(n − 2) = n diagonais que
não são paralelas a qualquer lado.
Problema 3.0.12 - Na década de 1960, tinha um programa semanal de televisão muito popular nos Estados
Unidos chamado "Let’s Make a Deal"("Vamos fazer um acordo"). A cada semana, em um determinado
momento no programa, o apresentador, Monty Hall, apresentava ao competidor três portas fechadas.
Atrás de uma das portas, havia um prêmio substancial (um carro) e atrás das outras, não havia nada substancial
(vamos imaginar que tivesse um bode). O apresentador, Monty Hall, pedia que o participante escolhesse uma
das porta. Claramente, a chance de o competidor escolher a porta com o prêmio era de 1 em 3. Para causar
impacto aos telespectadores, em vez de simplesmente abrir a porta escolhida para revelar o que está por trás,
o apresentador, Monty Hall, abria uma das duas portas que o competidor não tinha escolhido, revelando que
ela não escondia o prêmio (e sim um bode).
É claro que o apresentador sabia onde o prêmio estava, por isso ele podia fazer isso. Ele então oferecia ao
competidor a oportunidade de mudar sua escolha para a outra porta que, naquela momento, permanecia
fechada.
Qual é a estratégia mais lógica, ficar com a porta escolhida inicialmente ou mudar de porta? Com qual das
duas portas ainda fechadas o concorrente tem mais probabilidades de ganhar? Por quê?
Solução 1
27
Existem três portas: A, B e C. Quando o competidor escolheu uma delas, digamos a A, a chance de
que ela seja a premiada é de 1/3. Como conseqüência, a probabilidade de que tenha errado, ou em outras
palavras, de que o prêmio esteja nas outras duas portas B ou C é de 2/3. Pode-se comprovar isso somando a
probabilidade de cada uma das outras portas ou simplesmente sabendo que a probabilidade de que haja um
prêmio é sempre 1. O importante é ter em mente que a chance de o prêmio estar nas outras portas que ele
não escolheu é de 2/3. Entendendo isso, basta ver que o apresentador abrirá sem erro uma dessas outras
duas portas que contém um bode, digamos que seja a B. Ao fazer isso, ele está dando uma informação
valiosa: se o prêmio estava nas outras portas que não escolheu (B ou C), então agora ele só pode estar na
porta que o compettidor não escolheu e não foi aberta, ou seja, a porta C. Ou seja, se o competidor errou ao
escolher uma porta - e as chances disto são de 2/3 - então ao abrir uma das outras portas não-premiadas o
apresentador está lhe dizendo onde está o prêmio. Toda vez que o competidor tiver escolhido inicialmente
uma porta errada, ao trocar de porta irá com certeza ganhar. Como as chances de que tenha errado em sua
escolha inicial são de 2/3, se trocar suas chances de ganhar serão de 2/3 - e por conseguinte a chance de
que ganhe se não trocar de porta é de apenas 1/3. É assim mais vantajoso trocar de porta.
Solução 2
Suponha que, em vez de 3 houvessem 1000 portas, numeradas de 1 a 1000, e o competidor escolheu a
porta de número 1000.
Todos as portas contém um bode, exceto uma, aquela que tem o carro.
Quando o competidor escolhe uma porta, em seguida, Monty Hall abre todas as outras portas, exceto uma...
e dá a oportunidade para o competidor mudar a escolha para a outra porta. Se fosse você, mudaria? É
possível um pensamento do tipo "Escolhi a porta correta no meu primeiro palpite."Mas, qual é a probabi1
lidade de que isso fosse verdade? Resposta: 1000
... Há uma chance de 999 de que o carro não está atrás
da porta que o competidor escolheu. E se o carro não está atrás da porta que o competidor escolheu,
ele deve estar por trás da última porta que Monty deixou sem abrir. Em outras palavras, Monty ajudou,
deixando uma porta para que o competidor mude, que tem uma chance de 999 de ter o carro por trás dela.
999
Então nesse caso, se você mudar, você teria uma chance de 1000
de ganhar o carro. Portanto, é melhor mudar.
Problema 3.0.13 - Dois jogadores, A e B, disputam um jogo em que jogam alternadamente. Uma jogada de
A é escolher um ponto do plano, que não esteja pintado, e pintá-lo de vermelho. Uma jogada de B é escolher
10 pontos do plano, que não estejam pintados, e pintá-los de verde. O jogador A vence se existem três pontos
vermelhos que sejam vértices de um triângulo equilátero.
O jogador B pode impedir do jogador A de vencer a partida?
Solução
A resposta é não.
O primeiro jogador, A, pode sempre vencer, não importa como o jogador B jogue. Para isso, em suas
n primeiras jogadas ele escolhe pintar de vermelho pontos sobre uma mesma reta. Agora, observe que
para cada par destes n pontos existem dois pontos, um de cada lada da reta, que o segundo jogador,
B,tem de pintar de verde, para evitar que o jogador A vença. O números de tais pontosé igual a 2×
n
n
2 . Por outro lado, o jogador B pode pintar no máximo 10n pontos de verde. Agora, 2× 2 > 10n, que é
o mesmo que n(n − 1) > 10n. Ou seja, n − 1 > 10. Portanto, o primeiro jogador vence no seu 12o movimento.
Problema 3.0.14 - Ana e Célia disputam o jogo seguinte, em que jogam alternadamente. Ana deve pintar,
ou de azul ou de vermelho, cada ponto que esteja sobre um dado círculo. Célia deve escolher três dos pontos
pintados de modo que eles determinem um triângulo cujas medidas de seus ângulos internos sejam 30, 50 e
100 graus, respectivamente. Célia vence se esse triângulo possui os vértices de mesma cor. Ana vence se
Célia não consegue fazer a escolha.
Quem vence: Ana ou Célia?
Solução
28
Capítulo 3. Problemas Diversos
Ana vence.
Basta ela marcar 6 pontos sobre o círculo, de modo que este fique dividido em seis arcos de mesmo comprimento. Agora ela pinta alternadamente de azul e vermelho cada um dos arcos, de forma consecutiva, tendo
o cuidado de pintar em cada arco o ponto inicial da cor do arco, mas deixar o ponto final com a cor do
próximo arco. Quando Célia quiser escolher os vértices de seu triângulo, os extremos do lado oposto ao
ângulo de 600 , ela deve determinar um arco de 600 sobre o círculo. Pela pintura feita, estes extremos devem
necessariamente possuir cores distintas.
Problema 3.0.15 - Numa caixa, temos 25 fichas iguais, numeradas de 1 até 25. Você pode retirar da caixa
uma ficha por vez, sem reposição, e pode continuar a retirar fichas até que o produto de dois números de
duas fichas retiradas seja um quadrado perfeito.
Qual é o número mínimo de fichas que você deve retirar para ter certeza de obter um par de fichas cujo
produto é um quadrado perfeito?
Solução
Seja S = {1, 2, 3, ..., 24, 25}. Partimos o conjunto S em subconjuntos disjuntos com as seguintes duas
propriedades:
(i) o produto de quaisquer dois elementos de um subconjunto é um quadrado perfeito; (ii) o produto
de quaisquer dois elementos escolhidos em subconjuntos distintos não é um quadrado perfeito. Assim,
escrevemos:
S = {1, 4, 9, 16, 25} ∪ {2, 8, 18} ∪ {3, 12} ∪ {5, 20} ∪ {6, 24} ∪ {7} ∪ {10}∪
∪{11} ∪ {13} ∪ {14} ∪ {15} ∪ {17} ∪ {19} ∪ {21} ∪ {22} ∪ {23}
.
Ou seja, partimos o conjunto S em 16 subconjuntos disjuntos. Se escolhermos uma ficha de cada um
dos subconjuntos não teremos obtido um par de fichas satisfazendo ao problema. Mas, com mais uma ficha
vamos obter um par de fichas cujo produto é um quadrado perfeito. Portanto, a resposta é 16 + 1 = 17.
Problema 3.0.16 - Dois jogadores, A e B, disputam um jogo, em que jogam alternadamente. Inicialmente,
escreve-se no quadro-negro o número natural 2. Uma jogada consiste em somar ao último número, n, no
quadro-negro um divisor próprio de n. Quem atingir um número maior do que ou igual 2010 vence. O
jogador A começa o jogo.
Quem vence, A ou B? Qual é a estratégia para vencer?
Solução
O jogador A possui uma estratégia vencedora.
A estratégia do jogador A consiste em jogar deixando para seu adversário sempre um número ímpar. Observe
que um divisor próprio de um número ímpar é no máximo um terço daquele número, pois o menor divisor
deste número é 3. Deste modo, o jogador B só pode somar no máximo 13 do último número escrito no
quadro-negro.
Toda vez que o jogador B vai jogar, encontra um número ímpar e soma a ele um divisor dele, que é ímpar
também, resultando sempre num número par. O jogador A por sua vez soma sempre um divisor de um
número par. Assim, ele pode jogar a metade deste número e prossegue assim até obter pela primeira vez um
número maior do que ou igual a 1340. Uma vez obtido esse número x, o jogador A soma a ele sua metade,
atingindo então um número maior do que 2010. (Observe que: x+x
2 ≥ 2010 ⇒ x ≥ 1340).
Problema 3.0.17 - Dois jogadores, A e B, disputam o seguinte jogo, em que jogam alternadamente.
Escrevem-se no quadro-negro uma sequência de 49 números inteiros consecutivos quaisquer. Uma jogada
consiste em apagar um desses números. No final, restam somente dois números: a e b. O jogador A ganha se
MDC(a, b) = 1 e B ganha se MDC(a, b) > 1. O jogador A começa o jogo.
(a) Quem ganha: A ou B? Qual a estratégia para vencer?
(b) Se, em vez de 49 números inteiros consecutivos fossem 50, quem ganha: A ou B? Qual a estratégia para
vencer?
Solução
29
(a) O jogador A ganha.
Como a quantidade de inteiros é ímpar, o jogador divide os 49 primeiros números em pares de inteiros
sucessivos, deixando o número final sozinho. Ele inicia apagando o número que ficou sozinho. Se o jogador
B apaga qualquer número de um par, então A apaga o outro. O que sobra no final é um par (n, n + 1), com
MDC(n, n + 1) = 1.
(b) O jogador B ganha.
A estratégia do jogador B é apagar todos os números ímpares, deixando dois números ímpares múltiplos de
3. Por sua vez, o jogador A sempre apaga um número par. Antes da penúltima jogada restam quatro números
no quadro-negro: dois números pares, p e q, e dois números ímpares, i e j. Se A apagar um número ímpar,
então B apaga o outro número ímpar, restando os dois números pares. Se A apaga um dos números pares,
então B apaga o outro número par, restando i e j, com MDC(i, j) ≥ 3.
Problema 3.0.18 - Todo membro de uma seqüência de números, a partir do segundo, é igual a soma do
termo precedente com a soma de seus dígitos. O primeiro número da seqüência é 1.
Diga, justificando, se o número 2010 pertence à seqüência.
Solução
A resposta é não.
Seja (a1 , a2 , a3 , a4 , · · · a seqüência de números. Observe que:
a1 = 1,
a2 = 2 = 3.0 + 2,
a3 = 4 = 3.1 + 1,
a4 = 8 = 3.2 + 2,
a5 = 16 = 3.5 + 1,
a6 = 23 = 3.7 + 2,
a7 = 28 = 3.9 + 1,
···············
Para cada inteiro m, seja S(m) a soma dos dígitos de m. Sabe-se que, na divisão por 3,os números m e S(m)
deixam o mesmo resto. Observando os números da seqüência encontrados acima, temos que os restos da
divisão por 3 dos termos da seqüência são alternadamente 1 e 2. De fato, se an = 3k + 1, com k inteiro, então
an+1 = an + S(an ) = (3k + 1) + (3q + 1) = 3 j + 2, onde q e j são números inteiros inteiros.
Se an = 3k + 2, com k inteiro, então an+1 = an + S(an) = (3k + 2) + (3q + 2) = 3 j + 1, onde q e j são
números inteiros.
Deste modo, de fato o resto da divisão dos termos da seqüência por 3 é ou 1 ou 2. Mas, 2010 deixa resto
zero na divisão por 3. Portanto, 2010 não aparece na seqüência.
Problema 3.0.19 - (CRUX) No aniversário de Maria, José quer dar-lhe um presente e, para isso, propõe
o jogo seguinte, no qual eles jogam alternadamente. Ele escreve no quadro-negro os números inteiros
0, 1, 2, 3, 4, ...., 255, 256. Maria começa o jogo. Ela escolhe 27 dos números escritos e apaga-os. José escolhe
26 números dentre o que sobraram e apaga-os. Em seguida, Maria escolhe 25 dentre os números restantes
a apaga-os. E eles prosseguem assim até que José escolhe 20 = 1 número e apaga-o. Como são apagados
27 + 26 + 25 + 24 + .... + 21 + 20 = 28 ˘1 = 255 números, restam dois números, a e b, no quadro-negro, José
paga para Maria uma quantia, em reais, correspondente ao valor |a − b|.
Se os jogadores fazem sempre suas melhores jogadas, qual é o maior valor que Maria tem certeza que ganha?
Solução
Maria ganha no máximo 24 ou 216 reais.
A estratégia de Maria é apagar sempre os números que estão nas posições pares. Com isso, ela aumenta a
distância entre eles, aumentando o valor de |a − b|. Depois das jogadas de números 1, 2, 3 e 4, a distância
entre os números vizinhos, que estão ainda escritos no quadro-negro, é 2, 4, 6, 8 e 16, respectivamente, o que
garante a Maria receber o máximo possível, independente de como José joga.
30
Capítulo 3. Problemas Diversos
Problema 3.0.20 - (RP) Daniel tem uma balança de dois pratos e dez pedras cujos pesos são todos números
inteiros entre 1 até 10, inclusive. Ele quer colocar algumas pedras na balança de tal forma que os pratos
fiquem equilibrados.
(a) Determine qual é o maior e o menor número de pedras que pode colocar. Justifique por que é o maior e
mostre um exemplo.
(b) Determine a maior quantidade de pedras que se pode colocar se em cada prato se deve haver a mesma
quantidade de pedras.
Solução
(a) É impossível colocar 10 pedras, pois 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55, que é um número
ímpar e não pode ser dividido como soma de dois inteiros iguais. Nove pedras podem ser usadas, basta
retirar uma pedra cujo peso é um número ímpar. Por exemplo, se retirarmos a pedra 1, podemos colocar num
dos pratos as pedras 8 + 9 + 10 = 27 e no outro prato as pedras 2 + 3 + 4 + 5 + 6 + 7 = 27.
(b) O máximo possível de pedras que podemos usar é 8. Por exemplo, descartamos as pedras 9 e 10 e usamos
1 + 4 + 5 + 8 = 18 num dos pratos e 2 + 3 + 6 + 7 = 18 no outro prato.
Problema 3.0.21 - (OMP) Um motorista planeja uma viagem que vai passar por um trecho de 800 km no
deserto, que não possui postos para abastecer. Ele sabe que seu carro só pode armazenar 50 litros de gasolina
e tem um rendimento de 10 km por litro. O motorista pode deixar gasolina armazenada em barris, no costado
da rodovia, em pontos distintos dessa região desértica. Por exemplo, com o tanque cheio com 50 litros de
gasolina ele pode percorrer 100 km, deixar armazenado 30 litros no ponto que chegou e voltar ao ponto de
partida para reabastecer o tanque de gasolina. O motorista decide realizar a viagem e chega ao primeiro
posto antes do deserto com tanque vazio.
Pode o motorista atravessar o deserto se neste primeiro posto de abastecimento antes do deserto a oferta total
de gasolina é de 140 litros? E se fosse 180 litros?
Solução
Com a oferta de 140 litros não é possível o motorista atravessar o deserto.
Para atravessar o deserto se necessita armazenar gasolina no quilômetro 300 ou mais adiante, caso contrário,
se percorreria mais de 500 km sem abastecer, o que é impossível, pois a autonomia do carro é de no máximo
500 km. Chamemos este ponto de depósito de combustível de P. Para armazenar gasolina em P o motorista tem de percorrer pelo menos duas vezes a distância do primeiro posto ao ponto P, que é pelo menos
2 × 300 km = 600 km. Como a distância a ser percorrida é de 800 km, vemos que é impossível atravessar o
deserto com uma oferta menor do que 140 litros. Por outro lado, não se pode atravessar o deserto com uma
oferta exatamente igual a 140 litros, simplesmente porque é impossível armazenar gasolina em P e voltar
com esta quantidade.
Com 180 litros é possível atravessar o deserto seguindo o seguinte roteiro:
(a) O motorista faz três viagens para armazenar gasolina no ponto P, situado a 50 km da partida, armazenando
40 litros em cada uma das viagens;
(b) Após estas três viagens, abastece o tanque no primeiro posto com 30 litros, volta ao ponto P, chegando
com 25 litros;
(c) Do ponto P, avança duas vezes a um ponto Q a 100 km dele, armazenando ali 30 litros em cada viagem;
(d) De volta ao ponto P abastece com 45 litros que estão armazenados ali e segue até o ponto Q com 35 litros
de gasolina;
(e) A partir de Q, chegando num ponto R, armazenando ali 20 litros de gasolina e volta ao ponto Q;
(f) Abastece os 45 litros de gasolina restantes em Q, avança até R, chegando com 30 litros, abastece ali com
os 20 litros existentes no local e completa a viagem.
4. Legenda
4.1
Legenda
•
•
•
•
•
•
•
•
•
•
•
•
•
•
AMO - Australian Mathematical Olympiad
AUMO - All Union Mathematical (URRS)
BW - Baltic Way Mathematical Contest
CMO - Canadian Mathematical Olympiad
CRUX - Crux Mathematicorum (Revista de resolução de problemas - Canadá)
HMITMT - Havard-MIT Mathematics Tournaments
IMO - International Mathematical Olympiad
KMO - Kiev Math Olympiad
LMO - Lenigrad Mathematical Olympiad
OMM - Olimpiada Mexicana de Matemática
OMP - Olimpiada de Matemática do Peru
RP - Olimpiada Rioplatense de Matemática
SAMO - South African Mathematics Olympiad
TT - Tournament of the Tows
5. Bibliografia
1. ANGEL, D - http://math.stackexchange.com/questions/731193/how-to-win-this-game
2. EWING, J. - Paul Halmos: In his own words. Notice of AMS. Vol. 54 . Number 9. October 2007.
3. GUZMÁN, O. M. - Aventuras Matemáticas. Gradiva. Lisboa. 1990.
4. MARTÍN, J. E. - Resolucion de Problemas Matemáticos (Vol 3). Centro de Professores y Recursos.
Salamanca. 1999. (Em PDF)
5. POSAMENTIER, A.S.; WOLFGANG, S - The Art of Problem Solving. Corwin Press. Thousand
Oaks. 1996.
6. POSAMENTIER, A.S. - The Art of Solving Problems. Vienna 2-06 (Em PPT)
7. POSAMENTIER, A.S. - Problem Solving in Mathematics - Grade 3-6 Powerful Strategies to Deeper.
Corwin Press. Thousand Oaks. 2009.
8. ZEITZ, P. - The Art and Craft of Problem Solving. Second Edition. Wiley. Danvers. 2007