Universidade Federal de Sergipe

CAMPO MAGNÉTICO EM CONDUTORES
Introdução
A existência do magnetismo foi observada há cerca de 2500 anos quando
certo tipo de pedra (magnetita) atraía fragmentos de ferro, que são conhecidos
como ímãs permanentes. Descobriu-se que um ímã permanente exerce uma
força sobre outro ímã ou sobre um pedaço de ferro não imantado e que todo ímã
possui dois pólos: o pólo norte e o pólo sul. Os pólos magnéticos iguais de dois
ímãs se repelem mutuamente, enquanto pólos opostos se atraem.
A Terra é um imã natural de forma que a agulha de uma bússola alinhada
ao campo magnético da Terra é um exemplo de interação magnética. O pólo
norte geográfico da Terra está próximo ao pólo sul magnético, assim o pólo norte
da agulha de uma bússola aponta para o norte. Por volta de 1750, descobriu-se
que a força exercida por um pólo sobre outro variava com o inverso do quadrado
da distância entre os pólos.
Lei de Biot-Savart
A relação entre a eletricidade e o magnetismo foi descoberta no século
XIX quando Oersted verificou que a agulha de uma bússola era desviada por um
fio conduzindo uma corrente elétrica (Figura 1).
Figura 1: Experimento de Oersted. A agulha da bússola oscila
quando existe uma corrente e o sentido depende do sentido da
corrente (Sears & Zemansky).
Apostila de Laboratório de Física B – 2016/1
Departamento de Física, Universidade Federal de Sergipe
1
A partir do experimento de Oersted foi estabelecida a Lei de Biot-Savart
que estabelece o cálculo do campo magnético B originado por uma corrente I.
Para um condutor retilíneo, o módulo do campo magnético é dado por:
𝐵=
𝜇0 𝐼
2𝜋𝑟
(1)
onde µ0 = permeabilidade magnética do vácuo = 4.10-7 (T.m/A), r é a distância
entre o ponto do campo e o fio condutor e 𝐼 é a corrente no fio.
Neste caso, as linhas do campo magnético apresentam-se como círculos
concêntricos, o vetor B é perpendicular ao plano definido pelo ponto e o fio e o
sentido do campo é dado pela regra da mão direita (Figura 2).
Figura 2: Exemplo de uso da regra da mão direita para um condutor retilíneo.
Quando se aponta o polegar da mão direita no sentido da corrente elétrica, o
sentido do campo magnético é dado pelos demais dedos dobrados.
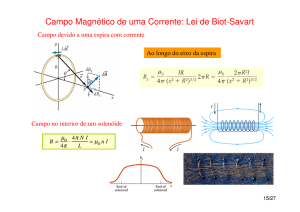
Considere agora uma espira circular de raio R e uma corrente I
percorrendo a espira (Figura 3). As linhas do campo magnético entram por um
lado da espira e saem por outro, de modo que o sentido é determinado pela regra
da mão direita.
Figura 3: O sentido do campo magnético de uma espira circular é dado pela
regra da mão direita.
Apostila de Laboratório de Física B – 2016/1
Departamento de Física, Universidade Federal de Sergipe
2
O módulo do campo magnético sobre o eixo de uma espira circular a uma
distância x do centro da espira é dado por:
𝜇0 𝐼𝑅 2
𝐵=
2(𝑥 2 + 𝑅 2 )3/2
(2)
Considerando que o ponto x = 0 é o centro da espira, tem-se que o módulo
do campo neste ponto é dado por:
𝜇0 𝐼
2𝑅
(3)
𝜇0 𝑁𝐼
2𝑅
(4)
𝐵=
E no caso de N espiras:
𝐵=
Lei de Ampère
A lei de Ampère é análoga à lei de Gauss para o campo elétrico. Essa lei
foi proposta originalmente por André-Marie Ampère no século XVIII e diz que “a
circulação do campo magnético ao longo de um percurso fechado é igual à
permeabilidade magnética no vácuo vezes a corrente total que atravessa a área
envolvida”, dada pela seguinte integral de linha:
(5)
∮ 𝐵. 𝑑𝑙 = 𝜇0 𝐼
A lei de Ampère é útil quando envolve situações com simetria que
permitem o cálculo da integral, tais como o cálculo do campo de um fio condutor
longo e retilíneo, campo no interior de um cilindro condutor, campo de um
solenóide linear, campo de um solenóide toroidal, entre outros.
Um solenóide é constituído por um enrolamento como uma hélice
cilíndrica com as espiras muito próximas (Figura 4). Todas as espiras conduzem
a mesma corrente I, e o campo magnético total B em cada ponto é a soma vetorial
dos campos produzidos pelas espiras individuais. No seu interior, os campos se
somam e o campo total é aproximadamente constante e uniforme. No seu
exterior, os campos se cancelam, e o campo é aproximadamente nulo.
Apostila de Laboratório de Física B – 2016/1
Departamento de Física, Universidade Federal de Sergipe
3
Figura 4: Campo magnético ao longo do eixo de um solenóide, cujo
comprimento é igual a quatro vezes o seu raio (Halliday; Sears & Zemansky).
Pela figura anterior, o número de espiras para um dado comprimento L é
igual a N. Cada uma dessas espiras passa uma vez pelo retângulo abcd e a
corrente total que passa pelo retângulo abcd é IT = NI
De acordo com a lei de Ampère, o módulo do campo magnético para um
solenóide longo é dado por:
𝐵 = 𝜇0
𝑁
𝐼
𝐿
(6)
onde µ0 = permeabilidade magnética do vácuo = 4.10-7 (T.m/A), I é a corrente
elétrica que passa pelo solenóide e N é o número de espiras em um dado
comprimento L.
Entretanto, o campo só é uniforme e constante na porção central do
solenóide, pois os solenóides reais têm comprimento limitado e os campos
próximos os limites do solenóide sofrem um efeito de borda, região na qual o
campo cai do valor do campo magnético no interior do solenóide até o campo
magnético nulo no exterior do solenóide. O comportamento do campo magnético
ao longo de um solenóide, incluindo a região de bordas, é representado na Figura
5 a seguir. Nesta figura, o valor do campo magnético em cada ponto foi dividido
pelo valor do campo máximo (B), no centro do solenóide (B0), e o comprimento
do solenóide pode ser estimado pela largura a meia altura, conforme indicado no
gráfico.
Apostila de Laboratório de Física B – 2016/1
Departamento de Física, Universidade Federal de Sergipe
4
Figura 5: Gráfico da razão entre o campo magnético (B) e o campo magnético
máximo (B0) no interior de um solenóide.
Atividade experimental
1. Objetivos
O objetivo desta atividade prática é contribuir para a compreensão do
campo magnético gerado por fios condutores, e observar na prática a Lei de BiotSavart e de Ampère.
2. Materiais e Métodos
Os materiais necessários para realização deste experimento são:
 Fonte de tensão elétrica contínua;
 Cabos;
 Teslâmetro;
 Multímetro;
 Bobinas condutoras;
 Bússolas;
 Fio de cobre;
 Solenóide com 300 espiras;
 Trena;
 Suportes diversos.
Apostila de Laboratório de Física B – 2016/1
Departamento de Física, Universidade Federal de Sergipe
5
Roteiro Experimental:
1ª Parte: Experiência de Oersted
i.
Monte um experimento semelhante ao de Oersted, utilizando uma bússola
e um suporte com um fio de cobre espesso.
ii.
Alinhe a bússola e o fio de cobre com a direção norte, como na Figura 1.
iii.
Aplique uma corrente de 3 A no fio e observe a deflexão da bússola.
iv.
Inverta a direção da corrente e observe novamente o que acontece.
2ª Parte: Campo central em bobinas de corrente (a Lei de Biot-Savart).
i.
Monte um arranjo experimental que permita a medida do campo no centro
das bobinas (x = 0).
ii.
Utilizando agora 3 bobinas de mesmo raio e com diferente número de
espiras, meça o campo magnético central em cada caso, utilizando uma
corrente fixa de 3 A.
iii.
Utilizando 3 bobinas com apenas uma volta e diferentes raios, meça o
campo magnético central em cada caso, utilizando uma corrente fixa de
3 A.
3ª Parte: Campo magnético central com diferentes correntes
i.
Meça o comprimento do solenóide e determine seu centro;
ii.
Insira a haste do teslâmetro no interior do solenóide até que a extremidade
coincida com o centro do solenóide. Essa será a posição x = 0;
iii.
Meça o valor campo magnético no centro do solenóide para 10 valores de
corrente distintos, menores do que 1,5 A, para determinar o valor de
corrente. Use o display da fonte como indicador da corrente.
4ª Parte: Campo magnético ao longo do eixo x
i.
Com o teslâmetro posicionado inicialmente na posição x = 0, ligue a fonte
de tensão e ajuste a corrente para 1 A;
ii.
Meça o valor do campo magnético na posição inicial e varie a posição da
extremidade da haste com relação ao centro do solenóide, medindo o
campo em cada posição, até que tenha sido possível obter os dados
necessários para construir um gráfico como o da Figura 5.
Apostila de Laboratório de Física B – 2016/1
Departamento de Física, Universidade Federal de Sergipe
6
3. Tabela de Dados
Tabela 1: Valores de campos magnéticos no centro de bobinas de diferentes
raios e número de espiras.
Bobinas de mesmo raio
Raio
(cm)
Nº de Campo Magnético em x=0 (mT)
Espiras Medida 1 Medida 2 Medida 3
B
(mT)
sa
(mT)
sb
(mT)
sc
(mT)
Resultado de B
Bobina1
(______±_____)_____
Bobina2
(______±_____)_____
Bobina3
(______±_____)_____
Bobinas de mesmo número de espiras
Raio
(cm)
Nº de Campo Magnético em x=0 (mT)
Espiras Medida 1 Medida 2 Medida 3
B
(mT)
sa
(mT)
sb
(mT)
sc
(mT)
Resultado de B
Bobina1
(______±_____)_____
Bobina2
(______±_____)_____
Bobina3
(______±_____)_____
Tabela 2: Valores de campos magnéticos no centro do solenóide para
diferentes correntes.
Campo magnético central (x=0)
Corrente sbcorrente
(A)
(A)
B
(mT)
sbcampo
(mT)
i1
i2
i3
i4
i5
i6
i7
i8
i9
i 10
Apostila de Laboratório de Física B – 2016/1
Departamento de Física, Universidade Federal de Sergipe
7
Tabela 3: Valores de campos magnéticos ao longo do eixo central do solenóide.
Campo magnético ao longo do eixo x
Corrente =
Deslocamento direção positiva
Deslocamento direção negativa
Posição
(cm)
0,0
1,0
2,0
3,0
4,0
5,0
6,0
7,0
7,5
8,0
8,5
9,0
9,5
10,0
10,5
11,0
11,5
12,0
12,5
13,0
13,5
14,0
B
(mT)
sb
(mT)
Apostila de Laboratório de Física B – 2016/1
Departamento de Física, Universidade Federal de Sergipe
Posição
(cm)
0,0
-1,0
-2,0
-3,0
-4,0
-5,0
-6,0
-7,0
-7,5
-8,0
-8,5
-9,0
-9,5
-10,0
-10,5
-11,0
-11,5
-12,0
-12,5
-13,0
-13,5
-14,0
B
(mT)
sb
(mT)
8
Discussão
1ª Parte:
1. Discuta a deflexão das bússolas devido à passagem de corrente no fio de
cobre.
2ª Parte:
1. Construa dois gráficos: um de campo magnético versus o número de
espiras e outro do campo magnético versus o raio da espira. Faça os
ajustes adequados em cada gráfico e determine, a partir dos parâmetros
dos ajustes, a permeabilidade magnética do ar, determine-a, com
incerteza (propagada) e compare, determinando o erro relativo em
percentual, com o valor da permeabilidade magnética do vácuo (4.10-7
T.m/A).
2. Discuta o comportamento dos gráficos e analise se os resultados estão
coerentes com a Lei de Biot-Savart (vide Equação (4)).
3ª Parte:
1. Construa o gráfico de B versus I e determine μ0 com incerteza (propagada)
a partir do coeficiente angular da reta, utilizando o valor de L determinado
com a régua e sabendo que o número de espiras do solenóide utilizado
era 300.
2. Compare o valor do item anterior com a permeabilidade magnética do
vácuo (4.10-7 T.m/A), mais uma vez determinando um erro relativo em
percentual.
4ª Parte:
1. Construa o gráfico de B/B0 versus a posição e verifique sua similaridade
com o gráfico da Figura 5. Note que B0 é o campo em x = 0 (valor máximo).
2. Determine o comprimento L do solenóide a partir do gráfico e compare
com o valor medido em sala.
Apostila de Laboratório de Física B – 2016/1
Departamento de Física, Universidade Federal de Sergipe
9