cópia_acetato_c_magnético3

Campo Magnético de uma Corrente: Lei de Biot-Savart
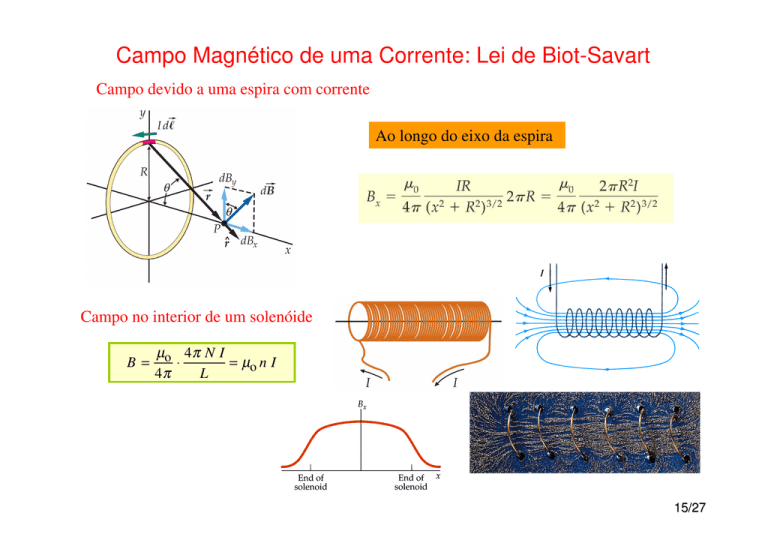
Campo devido a uma espira com corrente
Ao longo do eixo da espira
Campo no interior de um solenóide
B=
µo 4π N I
⋅
= µo n I
4π
L
15/27
15/27
Campo Magnético de uma Corrente: Lei de Biot-Savart
Campo devido a uma corrente rectilínea
Integrando a lei de Biot-Savart ao longo de todo o fio
obtemos a expressão do campo magnético para um
segmento rectilíneo do fio:
B=
µo I
⋅ ⋅ (s en θ1 + s e n θ2 )
4π R
onde R é a distância do fio ao ponto considerado e os
ângulos θ1 e θ2 têm o sentido definido na figura.
No caso dum fio infinito (θ1 = θ2 = 90°) obtém-se
B=
µo 2 I
µ I
⋅
= o
4π R
2π R
16/27
16/27
Lei de Ampère
A circulação do vector campo magnético através
duma curva fechada C é proporcional à corrente
enlaçada, I, por essa curva.
& &
∫C B ⋅ dl = µ 0 I
As correntes são consideradas de valor
positivo quando o seu sentido é o
definido pela regra da mão direita
quando se circula ao longa da curva C.
C
Exemplos:
I⊗
C
C
I
C
& &
∫C B ⋅ dl = µ 0 (I − I ) = 0
I
& &
∫C B ⋅ dl = 0
I
2I⊗
& &
∫C B ⋅ dl = µ 0 (I − 2 I ) = − µ 0 I
17/27
17/27
Campo criado por uma corrente rectilínea pela lei de Ampère
Configuração das linhas
de campo:
Orientação do campo
magnético:
Definição da curva
fechada C:
C
Definindo a circulação ao contrário obter-se-á
naturalmente a mesmo resultado:
& &
∫C B ⋅ dl = ∫C B dl cos180º = − B 2πr
C
& &
∫C B ⋅ dl = ∫C B dl cos 0 = B 2πr
e,
& &
e, ∫C B ⋅ dl = − µ 0 I
logo,
µ0 I
B=
2πr
logo,
& &
∫C B ⋅ dl = µ 0 I
µ0 I
B=
2πr
18/27
18/27
Campo criado por um solenóide infinito pela lei de Ampère
& &
& &
& &
& &
& &
∫C B ⋅ dl = ∫ab B ⋅ dl + ∫bc B ⋅ dl + ∫cd B ⋅ dl + ∫da B ⋅ dl = µ 0 nLI
I representa a intensidade de
corrente que percorre o solenóide e
portanto cada uma das espiras.
Sendo n o número de espiras por
unidade de comprimento, o
número de espiras N contidas no
comprimento L será, N = nL.
⇔
& &
∫C B ⋅ dl = ∫ab Bdl + 0 + 0 + 0 = µ 0 nLI
⇔
BL = µ 0 nLI
⇔
B = µ 0 nI
19/27
19/27
Força Magnética sobre uma Carga Pontual em Movimento
&
Quando uma carga eléctrica q& se move com velocidade v numa região onde
existe um campo magnético B fica sujeita a uma força magnética:
&
&
& &
F = q v × B ⇒ F = q v B senθ
A força é nula se a velocidade da carga for nula, ou seja, a força magnética só
actua sobre cargas em movimento.
– Mesmo estando a carga em movimento a força é nula se a sua velocidade
tiver a mesma direcção do campo magnético.
– Para uma dada intensidade do campo e uma dada velocidade, a força é
máxima quando o campo magnético e a velocidade são perpendiculares
entre si.
20/27
20/27
Movimento de uma Carga Pontual num Campo Magnético
•
A força magnética sobre uma carga em movimento é perpendicular à velocidade da
partícula.
A força magnética modifica a direcção da velocidade, mas não o seu módulo. Não altera a
energia cinética da partícula (não realiza trabalho).
•
No caso de a velocidade ser perpendicular a um campo magnético uniforme, a partícula
descreve uma órbita circular, caso contrário terá um movimento helicoidal.
Camp
o
•
uniform
e
v→
⊥ →
B
Camp
o
unifor
me
→
v não
perpen
dicular →
aB
Camp
o
não u
niform
e
→
v não
perpen
dicular →
aB
Caso existam campos eléctricos e magnéticos na mesma região do espaço, a partícula fica
& & &
sujeita a uma força resultante, denominada força de Lorentz: &
F = q ( E + v × B)
•
Com o auxílio de campos eléctricos e magnéticos é possível guiar partículas carregadas.
21/27
21/27