problemas de fsica ii

Problemas de Fluidos
DADOS:
ρágua = 1 g cm – 3 γágua = 0,073 N m–1 ρ mercúrio = 13,6 g cm – 3 γmercúrio = 0,514 N m–1
ρglicerina = 1,26 g cm – 3 ρar = 1,225 kg m – 3 g = 9,8 m s–2
Densidade; Pressão; Tensão Superficial; Capilaridade
3
1- Qual é a massa de um litro de óleo de caroço de algodão cuja densidade é de 0,926 g cm– ? E o peso?
3
2- A massa de um litro de leite é 1,032 kg. A nata que ele contém tem uma densidade de 0,865 g cm– ,
quando pura, e constitui 4% do volume do leite. Qual a densidade do leite desnatado?
5
3- A pressão atmosférica vale aproximadamente 1,013x10 Pa. Faça uma estimativa da intensidade da força
que a atmosfera exerce sobre a sua cabeça. Expresse o resultado em N e em kgf. (Considere φ = 10 cm)
4- Uma pessoa de 60 kg está em pé sobre uma caixa leve e cúbica de 5 cm de aresta. A caixa está assente no
chão. Qual a pressão que a caixa exerce sobre o chão?
5- Qual a força exercida pelo ar, em condições normais, na janela de uma sala, de dimensões 1,0 m x 1,5 m ?
6- Uma ventosa, com um diâmetro de 10 cm, é aplicada no tecto, para pendurar diversos objectos. Determine
o valor máximo de massa que pode ser pendurada, considerando que a pressão no interior da ventosa
corresponde a 1/10 da pressão atmosférica.
7- Um insecto de água assenta sobre a superfície desta sem se afundar devido
à tensão superficial. Se o insecto tiver seis patas, e cada pata estiver em
contacto com a água num comprimento de 5 mm, qual o peso máximo,
ou massa (em gramas), do insecto para que não se afunde?
8- A que altura sobe acima do nível do reservatório de água (a 20 ºC) num
tubo de vidro de diâmetro interno 2,0 mm ?
9- Calcule a depressão aproximada do mercúrio a 20 ºC num
tubo capilar de raio 1,5 mm. A tensão superficial ( γ ) para
–1
o mercúrio é de 0,514 N m a 20 ºC, a sua densidade é de
3
13,6 g cm– e o ângulo de contacto 140º .
FÍSICA II
Mecânica de Fluidos
Nova Edição 2005/2006
ESA – IPB
Lei Fundamental da Hidrostática; Medidores de Pressão; Lei de Pascal – Prensa hidráulica
10- Um dique, que protegia New Orleans, tinha uma fuga por um orifício de 1 cm2 de área, a 2 m de
profundidade abaixo da superfície da água.
Com que força deveria apertar uma pessoa sobre o orifício para deter a fuga?
Expresse o resultado em kgf.
11- Determine a pressão no fundo de um tanque
com glicerina sob pressão (Figura ao lado)
50 kPa
Glicerina
2,0 m
12- No séc. XVII, Pascal realizou a seguinte experiência:
encheu com água um barril de vinho, ao qual conectou um tubo
longo, onde foi acrescentando água até que rebentou o barril.
a) Se o raio da tampa fosse 20 cm e a altura do tubo 12 m, que força exercia a água sobre a tampa?
b) Qual a massa dessa água, se o tubo tivesse de diâmetro interno 6 mm?
13- A que altura a água poderia subir na canalização de um prédio, se a medida da pressão da água no
andar de térreo fosse 270 kPa ?
F2
14- Numa prensa hidráulica como a da figura ao lado, o pistão maior
2
tem uma área de secção transversal de 200 cm e o menor tem
2
uma área de 5 cm . Se uma pessoa de 50 kgf se colocar no pistão
menor, calcule a força F1 no pistão maior.
15- Para o sistema ao lado, o cilindro da esquerda, em L, tem uma
2
massa de 600 kg e uma secção de 800 cm . O pistão da direita,
L
2
em S, tem uma secção de 25 cm e peso desprezável. Se o sistema
3
for enchido com óleo (densidade = 0,78 g cm– ), calcule a força F
necessária para manter o sistema em equilíbrio.
A1
A2
F1
S
600 kg
8m
Lei de Arquimedes – Impulsão; Equação da Continuidade em Estado Estacionário e Não Estacionário;
Equação de Bernoulli
16- Um densímetro pesa 0,0216 N e tem na extremidade superior
uma haste cilíndrica de 2,8 mm de diâmetro. Quanto mais fundo
flutuará em óleo de densidade relativa 0,780 do que em álcool de
densidade relativa 0,821 ?
(Este instrumento tem vários nomes, consoante a escala de calibração:
Pesa – Mosto (saber a quantidade de açúcar no mosto);
Pesa – Sais (saber a densidade de líquidos mais densos que a água);
Pesa – Vinho (uma espécie de enómetro, permite saber o álcool presente no vinho).
FÍSICA II
Mecânica de Fluidos
Nova Edição 2005/2006
ESA – IPB
17- Um pedaço de uma certa liga pesa 86 gf no ar e 73 gf quando imerso em água. Calcule o seu volume e a
sua densidade.
18- Uma tampa de vidro pesa 2,50 gf no ar, 1,50 gf na água e 0,70 gf no ácido sulfúrico. Qual é a densidade
do ácido? E a sua densidade relativa?
3
19- Suspeita-se que um pedaço de ouro puro (ρ = 19,3 g cm– ) tenha o centro oco. Ele pesa 38,25 gf no ar e
36,22 gf na água. O objecto é oco ou maciço?
3
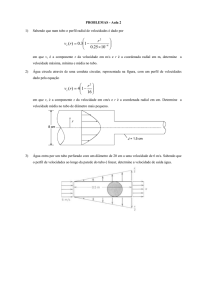
20- Quando 0,03 m s–1 de um fluido ideal se escoam através de um tubo de 300 mm que mais tarde se reduz
a um tubo de diâmetro 150 mm, calcule as velocidades médias nos dois tubos.
21- Se a velocidade, de um fluido ideal, num tubo de 300 mm for de 0,50 m s–1, qual será a velocidade num
jacto de 75 mm de diâmetro saindo de um bocal fixo ao tubo?
3
22- Se 250 cm de um fluido ideal se escoarem por um tubo de 7 mm, em 7 s, qual a velocidade média do
fluido no tubo?
23- A mangueira de um jardim possui um diâmetro de 2 cm e está ligada a um irrigador que consiste num
recipiente munido de 20 orifícios, cada um dos quais com diâmetro de 0,14 cm. A velocidade da água na
mangueira vale 0,85 m s–1. Calcule a velocidade da água ao sair dos orifícios.
3
24- Um tubo cilíndrico transporta óleo. A densidade do óleo vale 0,85 g cm– . Ao passar pela secção recta do
tubo, a velocidade é constante e igual a 1,2 m s–1. O diâmetro vale 10 cm. Calcule: (a) o caudal; (b) o
fluxo de massa.
3
25- No aparelho ao lado, uma misturadora, alimenta-se água através do tubo A, a um caudal de 0,10 m s–1,
enquanto que glicerina, cuja densidade relativa é de 1,26, é alimentada pelo tubo B a um débito de 0,030
3
m s–1. A emulsão, de densidade relativa 1,05, sai pelo tubo C de 30 cm de diâmetro
Determine a produção ao fim de uma hora,
a) em litros;
A
C
b) em kg .
B
A
B
2
hA
hB
1
3
1,5 m
FÍSICA II
26- Água está a fluir para dentro do tanque paralelipédico A. A base
deste tanque é quadrada, de aresta 1,5 m. O caudal na conduta (1)
3
que alimenta o tanque A, é de 3,55 m s–1. A água escoa-se para o
tanque B, também de base quadrada com aresta de 2,5 m, com
3
um caudal de 1,82 m s–1. Determine:
a) a variação do nível de água no tanque A em função do tempo;
b) o tempo que demora a encher o tanque A (h= 1,5 m);
b) c) o caudal que atravessa a secção (3), sabendo que a superfície livre
do tanque B desce a uma velocidade de 6,1 cm s–1.
2,5 m
Mecânica de Fluidos
Nova Edição 2005/2006
ESA – IPB
27- Um tubo horizontal onde ocorre um escoamento de água tem um estrangulamento, com mostra a figura ao
lado. No ponto 1, o diâmetro vale 6 cm, a velocidade 2 m s–1 e a pressão 180 kPa. No ponto 2, o diâmetro
vale 2 cm. Determine a velocidade e a pressão no ponto 2.
2
1
28- Num tubo de Venturi, equipado com um manómetro de mercúrio,
o ponto 1 tem o diâmetro de 12 cm, enquanto que no ponto 2
o diâmetro é 6 cm. Qual o fluxo Q de água no tubo de Venturi,
se a leitura no manómetro for 22 cm ?
3
(A densidade do mercúrio é igual a 13,6 g cm– .)
1
29- Que volume de água sairá, por minuto, de um tanque destapado
através de uma abertura de 3 cm de diâmetro que está 5 m abaixo
do nível da água no tanque ?
5m
2
30- Um tubo de Pitot é montado na asa de um avião para determinar a velocidade do aparelho em relação ao
ar, que está à temperatura de 0 ºC. O tubo contém álcool e indica uma diferença de altura nos níveis de 26
2
3
cm. Qual a velocidade do avião em relação ao ar ? Considere a densidade do álcool igual a 8,1x10 kg m– .
FLUIDOS REAIS: Lei de Poiseuille; Número de Reynolds
31- Quanta água se escoará em 30 s, através de um tubo capilar de 200 mm de comprimento e de diâmetro
interno 1,5 mm, se a diferença de pressão através do tubo é de 5 cm-Hg ? A viscosidade da água é 0,801
3
cP e a densidade do mercúrio, 13,6 g cm– .
32- Uma artéria de uma pessoa foi reduzida a metade do seu diâmetro original devido a depósitos na parede
interna. Qual o factor de redução do fluxo de sangue, se a diferença de pressão ao longo da artéria
permanecer inalterada ?
33- Determine a velocidade crítica de um escoamento, a 20 ºC, num tubo de 20 mm (a) para a gasolina;
-7 2
-6 2
(b) para a água. (Viscosidade: 6,48x10 m s–1 – gasolina; 1,02x10 m s–1 – água.)
34- Determine o tipo de escoamento que ocorre num tubo de 305 mm quando (a) água a 15 ºC escoa a uma
velocidade de 1,07 m s–1 , e (b) óleo combustível pesado, a 15 ºC, escoa à mesma velocidade.
-7 2
-5 2
(Viscosidade: 11,3x10 m s–1 – água; 20,53x10 m s–1 – óleo combustível.)
3
35- Para condições de escoamento laminar, que diâmetro de tubo conduzirá 0,0057 m s–1 de óleo
-6 2
combustível a 4 ºC ? (viscosidade = 6,09x10 m s–1)
Bibliografia:
“Física Geral”, Frederick J. Bueche, Schaum McGraw-Hill, São Paulo – Brasil, 1983
“Mecânica de Fluidos e Hidráulica”, R. V. Giles & et. al., Makron Books, Brasil, 1996
“Engineering Fluid Mechanics”, J. A. Roberson & C. T. Crowe, Wiley & Sons, 1997
FÍSICA II
Mecânica de Fluidos
Nova Edição 2005/2006
ESA – IPB
SOLUÇÕES
Procurou-se Respeitar os Algarismos Significativos
1) 0,9 kg ; 9 N
–3
2) 1,039 g cm
2
3) 8,0 x10 N; 80 kgf
5
4) 2 x 10 Pa
5) -----6) 73 kg
7) 0,2 g
8) 7,4 mm
9) – 8 mm
10) 24 m (óleo) ; 18 m (água)
11) 75 kPa
12) 13 atm
13) 17 m
14) 2000 kgf
15) 184 N
16) h = 1,05 h
1
2
3
17) 13 cm ; 6,6 g cm
–3
–3
18) 1,8 g cm ; 1,8
3
–3
19) 0,05 cm (Densidade do objecto = 18,8 g cm . O objecto é oco.
–1
–1
20) v = 0,42 m s ; v = 1,70 m s
1
2
–1
21) 8 m s
22) 0,9 m s
–1
–1
23) 9 m s
–1
–1
24) 9,4 l s ; 8,0 kg s
5
5
25) 4,7 x 10 litros; 5,0 x 10 kg
–1
3 –1
26) a) + 77 cm s ; b) 4,3 min c) 2,2 m s
–1
27) 18 m s ; 20 kPa
–1
3
28) 0,02 m s
–1
3
29) 0,42 m min
–1
30) 200 km h
3
31) 155 cm
32) 0,062
–1
–1
33) 0,065 m s ; 0,10 m s
34) a) escoamento turbulento; b) escoamento laminar
35) 0,60 m
FÍSICA II
Mecânica de Fluidos
Nova Edição 2005/2006
ESA – IPB