LISTA IV – Tensão Normal e Cisalhamento

TENSÃO NORMAL e TENSÃO DE CISALHAMENTO
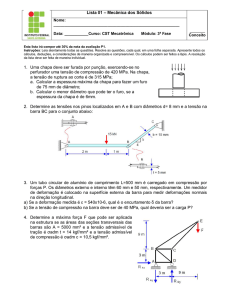
1) Determinar a tensão normal média de compressão da figura abaixo entre:
a) o bloco de madeira de seção 100mm x 120mm e a base de concreto.
b) a base de concreto 500mm x 500mm e o solo.
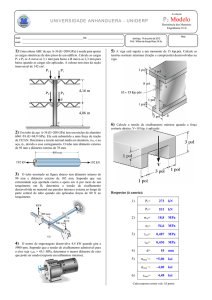
2) Calcular as tensões de "contato" em A, B e C, na estrutura representada
na figura abaixo. (dimensões em metros)
3) A carga de ruptura por tração de uma barra redonda de aço, com diâmetro
de 20 mm, é de 12.500 kg. Qual é a resistência à tração desse aço e qual é o
coeficiente de segurança existente quando σadm= 1.400 kg/cm² ?
4) Emprega-se um rebite para ligar duas barras de aço, como se indica na
figura. Se o diâmetro do rebite é 19mm e a carga P = 30 kN, qual a tensão
de cisalhamento no rebite?
5) Determine as tensões normais desenvolvidas nas seções de topo, meia
altura e base, no pilar abaixo. O peso próprio do pilar deve ser considerado.
(peso específico: 30 kN/m3)
6) Um pilar de concreto recebe uma carga axial de 200 kN. Dimensione-o
com seção quadrada de lado “a” levando em conta que a tensão admissível
de compressão para este concreto é de 2,0 kN/cm2. Dimensione também o
seu bloco de fundação, com seção igualmente quadrada e lado “b”, sabendo
que o solo onde o sistema assenta tem uma tensão de compressão
admissível de 0,025 kN/cm2. (DICA: O peso próprio do material deve ser
considerado). Dados : γconcreto= 25 kN/m3.
7) Duas peças de madeira de seção retangular 80mm x 140mm são coladas
uma à outra em um entalhe inclinado, conforme mostra a figura abaixo.
Calcular as tensões na cola para P = 16 kN e para:
a) θ = 30º ; b) θ = 45º ; c) θ = 60º
8) Um pilar em aço deve receber uma carga oriunda de um telhado de 60 kN.
Dimensione-o com seção quadrada sabendo que o aço apresenta peso
específico de 77 kN/m3 e tem uma tensão de compressão admissível de 8
KN/cm2.
9) As peças de madeira A e B são ligadas por cobrejuntas de madeira que
são colados nas superfície de contato com as peças. Deixa-se uma folga de
8 mm entre as extremidades de A e B . Determine o valor do comprimento
"L" para que a tensão de cisalhamento nas superfícies coladas não
ultrapasse 0,8 kN/cm2.
10) Uma placa é fixada a uma base de madeira por meio de três parafusos
de diâmetro 22mm. Calcular a tensão média de cisalhamento nos parafusos
para uma carga P=120 kN, conforme mostra a figura abaixo.
11) O elemento AC mostrado na figura está submetido a uma força vertical
de 3 kN. Determinar a posição x de aplicação da força de modo que a tensão
de compressão média no apoio C seja igual à tensão de tração no tirante AB.
A haste tem uma área de seção transversal de 400 mm², e a área de contato
em C é de 650 mm².
12) A barra mostrada na figura tem seção transversal quadrada para a qual a
profundidade e a largura são de 40 mm. Supondo que seja aplicada uma
força axial de 800 N ao longo do eixo do centróide da área da seção
transversal da barra, determinar a tensão normal média e a tensão de
cisalhamento média que atuam sobre o material (a) no plano da seção a-a e
(b) no plano da seção b-b.
13) Uma chapa deve ser furada por punção, exercendo-se no perfurador
uma tensão de compressão de 420 MPa. Na chapa, a tensão de ruptura ao
corte é de 315 MPa;
a) Calcular a espessura máxima da chapa para fazer um furo de 75 mm de
diâmetro;
b) Calcular o menor diâmetro que pode ter o furo, se a espessura da chapa é
de 6mm.
14) Uma placa metálica onde são colocados equipamentos pesados é
apoiada em 4 pilaretes de seção circular vazada feitos de ferro fundido. Cada
um desses pilaretes deve ser projetado para resistir a uma força de 280 kN.
Se a tensão de ruptura do ferro fundido é 350 MPa, o coeficiente de
segurança com relação à ruptura é 4, e a espessura da parede dos pilaretes
é 10mm, qual o diâmetro externo mínimo que os pilaretes devem ter? (ver a
figura abaixo).
15) O elemento inclinado na Figura abaixo está submetido a uma força de
compressão de 3.000 N. Determine a tensão de compressão média ao longo
das áreas de contato lisas definidas por AB e BC e a tensão de cisalhamento
média ao longo do plano horizontal definido por EDB.
16) A luminária de 80 kg é suportada por duas hastes AB e BC como mostra
a figura. Se AB tem diâmetro de 10 mm e BC tem diâmetro de 8 mm.
Determinar a tensão normal média em cada haste.
17) O conjunto consiste em três discos A, B e C usados para suportar a
carga de 140 kN. Determine o menor diâmetro d1 do disco superior, o
diâmetro d2 do espaço entre os apoios e o diâmetro d3 do orifício no disco
inferior. A tensão de apoio admissível para o material é (σadm)a = 350 MPa e
a tensão de cisalhamento admissível é τadm = 125 MPa.
18) A escora de madeira mostrada na figura está suportada por uma haste
de aço de 10 mm de diâmetro presa na parede. Se a escora suporta uma
carga vertical de 5 kN, calcular a tensão de cisalhamento média da haste e
ao longo das duas áreas sombreadas da escora, uma das quais está
identificada como abcd.
19) O tirante está apoiado em sua extremidade por um disco circular fixo
como mostrado na figura. Se a haste passa por um furo de 40 mm de
diâmetro, determinar o diâmetro mínimo requerido da haste e a espessura
mínima do disco necessários para suportar uma carga de 20 kN. A tensão
normal admissível da haste é σadm = 60 MPa, e a tensão de cisalhamento
admissível do disco é τadm = 35 MPa.
20) A coluna está sujeita a uma força axial de 8 kN aplicada no centroide da
área da seção transversal. Determine a tensão normal média que age na
seção a-a. Mostre como fica essa distribuição de tensão sobre a seção
transversal da área.
21) A barra rígida mostrada na figura é suportada por uma haste de aço AC
que tem diâmetro de 20 mm e um bloco de alumínio que tem área da seção
transversal de 1800 mm². Os pinos de 18 mm de diâmetro em A e C estão
submetidos a um cisalhamento simples. Se a tensão de ruptura do aço e do
alumínio forem (σaço)rup = 680 MPa e (σal)rup = 70 MPa, respectivamente, e
a tensão de cisalhamento de ruptura de cada pino for τrup = 900 MPa,
determinar a maior carga P que pode ser aplica à barra. Aplicar F.S = 2.
22) As hastes AB e CD são feitas de aço cuja tensão de ruptura por tração é
σrup = 510 MPa. Usando um fator de segurança FS = 1,75 para tração,
determine o menor diâmetro das hastes de modo que elas possam suportar
a carga mostrada.
23) O punção circular B exerce uma força de 2 kN no topo da chapa A.
Determinar a tensão de cisalhamento média na chapa devida a esse
carregamento.
24) O bloco de concreto tem as dimensões mostradas na figura. Se o
material falhar quando a tensão normal média atingir 0,84 MPa, determine a
maior carga vertical P aplicada no centro que ele pode suportar.
25) O pequeno bloco tem espessura de 5 mm. Se a distribuição de tensão no
apoio desenvolvida pela carga variar como mostra a figura, determine a força
F aplicada ao bloco e a distância d até o ponto onde ela é aplicada.
26) O elemento B está sujeito a uma força de compressão de 4 kN. Se A e B
forem feitos de madeira e tiverem 10 mm de espessura, determine, com
aproximação de 5 mm, a menor dimensão h do apoio de modo que a tensão
de cisalhamento média não exceda τadm = 2,1 MPa.
27) A junta está presa por dois parafusos. Determine o diâmetro exigido para
os parafusos se a tensão de ruptura por cisalhamento para os parafusos for
τrup = 350 MPa. Use um fator de segurança para cisalhamento FS = 2,5.
28) Se a tensão de apoio admissível para o material sob os apoios em A e B
for σadm = 2,8 MPa, determine os tamanhos das chapas de apoio quadradas
A’ e B’ exigidos para suportar a carga. Considere P = 7,5 kN. A dimensão
das chapas deverá ter aproximação de 10 mm. As reações nos apoios são
verticais.