r 0 - PRP

INTERAÇÃO ENTRE CARGAS COM A ELETRODINÂMICA DE WEBER
Aluno: Alexandre Gomes Pinto. E-mail: [email protected]
Orientador: André Koch Torres Assis. E-mail: [email protected]
INSTITUTO DE FÍSICA “GLEB WATAGHIN”, UNICAMP, 13083-859, Campinas,SP
Trabalho de iniciação científica realizado com bolsa de fomento FAPESP
Palavras chave: Weber-Eletrodinâmica-Indutância
Introdução
Resultados
A eletrodinâmica de Weber é baseada em uma força entre cargas que depende da
distância, velocidade e aceleração entre elas. É uma força central derivada de uma energia
potencial, logo satisfaz às leis de conservação de energia, momento linear e angular. A
motivação de Weber ao propor sua eletrodinâmica em 1846 foi unificar em uma única
fórmula as forças de Coulomb e Ampère, além da lei de indução de Faraday. De acordo com
a lei de Weber, a força exercida pela carga q’ sobre a carga q, é dada por:
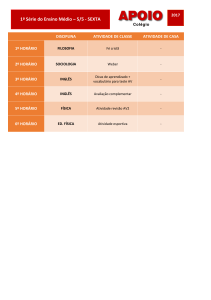
Os períodos de oscilação obtidos para um sistema de cargas opostas, usando os potenciais
de Coulomb e de Weber, foram , respectivamente,

Fq 'q
q' q rˆ
r²
1
4 0 r²
2c ²
rr
c²
(1)
Este projeto tem como objetivo geral a familiarização com a eletrodinâmica de Weber.
Para isso, será apresentada a análise de dois tópicos: o problema unidimensional de dois
corpos interagindo pelo potencial de Weber e a derivação da indutância de um circuito,
utilizando a segunda lei de Newton em conjunto com a força de Weber. Para o primeiro
tópico, vamos comparar o período de oscilação obtido por Weber com o obtido usando o
potencial coulombiano. Veremos ainda que a interação pelo potencial de Weber permite uma
situação nova que não ocorre no eletromagnetismo clássico, a saber, o movimento
oscilatório entre duas cargas de mesmo sinal. Weber usou este fato para propor um modelo
planetário para os átomos no qual o núcleo era mantido estável apenas por sua força
eletromagnética. No segundo tópico, veremos que a indutância de um circuito pode ser vista
como uma medida da massa inercial efetiva dos elétrons.
TC
2
2
0
qq'
3/ 2
0
r
e
TW
4
2
0
qq'
r0
3/ 2
0
r
r0
r0
2
arctan
r0
(4)
onde μ = mm’/(m+m’) é a massa reduzida do sistema e ρ = qq’/(4πε0μc²) é uma constante
característica do sistema, com unidade de distância. A análise das fórmulas indica que o
período de Weber coincide com o de Coulomb para r0 >> ρ, sendo então o quadrado do
período proporcional ao cubo da distância inicial entre as cargas. Este resultado é análogo a
terceira lei de Kepler do movimento planetário. Na Figura 2 temos o comportamento dos
dois períodos em função de r0.
Metodologia
Problema de dois corpos: Consideramos duas partículas pontuais de cargas q e q’ e
massas m e m’ , partindo do repouso em relação a um referencial inercial, a uma distância r0
uma da outra. As expressões de velocidade de aproximação/repulsão das cargas podem ser
derivadas a partir do princípio de conservação de energia, E = T+U = constante, onde T é a
energia cinética das duas cargas e U a energia potencial de Coulomb ou de Weber. Esta
última é dada por:
U
1
4
0
qq'
r²
1
r
2c ²
(2)
Essa energia potencial reduz-se à de Coulomb quando a velocidade entre as cargas é nula.
Com as expressões de velocidade, foi possível calcular analiticamente o tempo para que as
cargas voltassem às condições iniciais. Vale lembrar que supomos uma situação idealizada,
na qual as partículas passam uma pela outra quando se encontram, sem que haja colisão.
A derivação da auto-indutância de um circuito pode ser feita considerando a equação
de movimento de um único elétron em condução. Considerando que sobre esse elétron
atuam a força de Weber FW e uma força de resistiva –bv dependente da velocidade v do
elétron em relação ao condutor, temos, pela segunda lei de Newton, que FW - bv = ma .
Com isso, podemos chegar à equação de um circuito resistivo-indutivo, a saber:
V (t )
dI
L
dt
RI
d ²Q
L
dt ²
dQ
R
dt
As configurações estudadas são mostradas na Figura 1.
(3)
Figura 2: Períodos de oscilação do sistema elétron-próton segundo Weber (1) e Coulomb (2)
para (a) 0 < r0 < 2ρ e para (b) r0>>ρ.
Para um sistema de cargas de mesmo sinal, segundo a eletrodinâmica de Weber o
movimento será oscilatório se a distância inicial r0 for menor que a distância crítica ρ. Caso
contrário, a distância entre as cargas aumenta cada vez mais, que é o caso não-oscilatório,
análogo à repulsão coulombiana. O período obtido para r0< ρ, com ρ>0, é:
TW
2 2
r0
c
r0
(
r0
r0 ) ln
r0
(5)
Para interações entre prótons e elétrons com uma distância inicial de 1 Å, temos as
seguintes frequências de oscilação: 1/TC =1/ TW ≈ 1015 Hz, ou seja, com ordem de grandeza
da luz visível. Já para o sistema próton-próton, para qualquer distância r0 < ρ, temos que
1/TW > 1020 Hz, que é a região dos raios gama, cuja origem é tida como resultado de
processos nucleares.
Quanto ao cálculo da indutância de um circuito, obtivemos que, além do termo
coulombiano, somente é não-nulo o termo que leva em conta a aceleração relativa entre o
elétron de condução e a rede cristalina, considerando que a f.e.m. do circuito varia
lentamente. Podemos escrever a força proveniente deste termo como F = mWa, onde mW é
uma massa weberiana do circuito. Ocorre que mW é muito maior que a massa do elétron, de
maneira que a indutância fica em função apenas da massa weberiana, que depende da
geometria do circuito. Pelo cálculo da indutância nos circuitos da Figura 1, obtivemos que,
para distribuições volumétricas ou superficiais de carga, temos, respectivamente,
L
mW 
e A
ou
L
mW 
e s
(6)
Isso justifica a semelhança entre (3) e a equação de movimento forçado amortecido, que é:
F (t )
d ²x
m
dt ²
dx
b
dt
(7)
Conclusão
Figura 1: Circuitos para os quais foram derivadas as indutâncias pela lei de Weber.
Obtivemos uma expressão analítica para os períodos de oscilação de um sistema de
duas cargas, movimentando-se na linha que as une. Ao colocar os valores conhecidos das
massas e cargas dos prótons e elétrons, obtém-se na eletrodinâmica de Weber frequências de
oscilação das partículas de mesma ordem de grandeza da luz visível ou dos raios gama. Isso
não deve ser coincidência, embora ainda não esteja elucidada a relação entre os fenômenos.
A indutância de um circuito pode ser considerada como uma medida da massa inercial
efetiva dos elétrons, mostrando que a semelhança entre as equações (3) e (7) não é
coincidência.