Colégio Zaccaria TELEFAX: (0 XX 21) 3235

EXERCÍCIO DE MATEMÁTICA
Prova Final
Colégio Zaccaria
TELEFAX: (0 XX 21) 3235-9400
www.zaccaria.g12.br
Data:
Aluno(a): _________________________________________________
Turma: 1801/02
Turno: Manhã
N.º ____
Professor(a): Marinete
CONTEÚDOS:
ÁLGEBRA:




Fatoração de polinônios.
Simplificação de frações algébricas.
Equações fracionárias e problemas.
Sistema de equações fracionárias.
GEOMETRIA:



Triângulos.
Quadriláteros.
Círculo e Circunferência.
1) Simplifique ao máximo as frações algébricas, depois de fatorar os polinômios:
a)
x 2  10 x  25
x 2  25
b)
ax  bx  ay  by
a2  b2
c)
a 2  3a
a 2  6a  9
d)
3x 2 y  3xy 2
x 2  2 xy  y ²
1
2) Qual é o conjunto solução da equação:
2
4x
7
 2

?
x3 x 9 x3
3) Para que valor de y a igualdade abaixo é verdadeira?
10
15
13


3y  6 2 y  4 6
4) A razão entre a idade que Fabiana terá daqui a 5 anos e a idade que ela tinha há 5 anos é de
3
.
2
Resolva os itens a seguir:
a) Qual é a equação que melhor representa a situação citada?
b) Qual é a idade atual de Fabiana?
2
5) Resolva os sistemas, usando qualquer dos métodos estudados, dando seu conjunto solução:
S = x, y  , verificando o conjunto universo.
a)
1
 2
1  y  1  x

b) 
x  5 1
 y
 x 1
5

 y
x  4 y  3

6) Trezentos e vinte livros deveriam ser repartidos igualmente entre alguns alunos de uma escola. No
entanto três deles deixaram de comparecer e o total de livros distribuídos foi alterado para 296.
Responda:
a.
Qual era o número inicial de alunos?
b.
Quantos alunos compareceram no dia da distribuição dos livros?
c.
Quantos livros cada aluno recebeu?
3
7) Numa loja de produtos esportivos, há uma promoção para quem comprar acima de oito unidades
de um mesmo produto. A fórmula utilizada pelo gerente para obter o preço unitário do produto é:
P=
k
 15
n
k = Valor constante que depende do tipo
do produto (em reais)
n = Número de unidades adquiridas (n ≥ 8)
P = Preço unitário do produto (em reais)
Qual o valor da constante k, sabendo-se que determinado cliente comprou 20 camisetas de
basquete por R$ 23,00 cada?
a)
b)
c)
d)
K = 120
K = 160
K = 140
K = 210
8) Uma indústria produziu 150 peças em x dias. Se tivesse trabalhado (3x -1) dias, produziria 420 peças.
Nessa indústria, a produção diária é sempre a mesma.
a) Em quantos dias foram produzidas as 150 peças?
b) Qual é a produção diária dessas peças?
c) quantas peças podem ser produzidas em 10 dias?
4
8) Em um triângulo, a medida de seus ângulos são expressa s por 3x, 4x + 15° e 6x– 30°.
Qual é a medida do maior ângulo desse t riângulo?
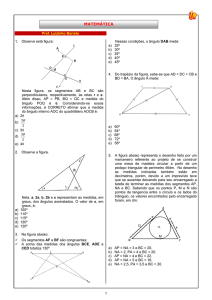
9) Na f igur a abaixo, calcule z:
A
z
30º
100º
B
50º
D
C
H
10) Num tr iângulo isósceles, o ângulo do vért ice mede o dobro de cada ângulo da base.
Quanto mede cada ângulo desse triângulo?
11) Determine o valor de x e y da figura abaixo, sabendo-se que o triânculo ABC é isósceles, de
base BC.
A
x y
60º
D
80º
B
C
5
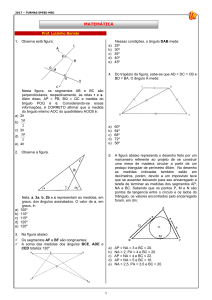
12) A figura abaixo é um trapézio isósceles. Sabendo que AM está contido na bissetriz do ângulo DAˆ B e BM
está contido na bissetriz do ângulo CBˆ A , determine o valor da medida x indicada.
C
D
108º
M
x
A
B
13) O retângulo abaixo, possui lados medindo x e y.
y
x
Responda:
a) Qual é o monômio que representa a sua área?
b) Qual é o polinômio, na forma reduzida, que representa seu perímetro?
c)
Qual é a forma fatorada do polinômio do item b?
14) As medidas a, b e c dos ângulos centrais indicados, são dados pelas expressões a = 5x + 10º,
b = 4x + 30º e c = x + 80º. As medidas dos ângulos a, b e c são respectivamente.
a) 130º, 124º e 106º.
b) 120º, 134º e 106º.
c) 180º, 134º e 106º.
d) 120º, 180º e 106º.
15) O valor de  na figura é
a) 25º
b) 30º
c) 40º
d) 45º
6
16) Qual é o valor de x, se B divide o arco AB em dois arcos congruentes?
7