Ficha nº2

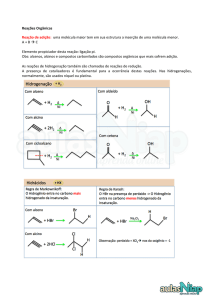
Mestrado em Física e Química, ano lectivo 2005/6
1
ESPECTROSCOPIAS ROTACIONAL E VIBRACIONAL
1. Gillian observou uma risca no espectro rotacional de micro-ondas de 12C16O no seu estado
fundamental a 3.84235 cm-1, enquanto que para o 13C16O a risca aparece a 3.67337 cm-1. As
massas atómicas relativas são m12C = 12.0000 e m16O = 15.9949.
a) Calcule o comprimento da ligação 12C16O. R: 1.132 10-10 m
b) Determine a massa atómica relativa do 13C. R: m13C = 12.9626
2. O espectro de infravermelho do HBr gasoso inclui uma banda intensa centrada a 2559 cm-1
cujas linhas sucessivas estão afastadas de 1654 cm-1. Se a constante de anarmonicidade for
0.01706, calcule
a) a distância internuclear de equilíbrio. R: r0 = 1.432 10-11 m
b) o número de onda da vibração fundamental. R:  = 2649 cm-1
c) o número de onda a que pertence o segundo harmónico. R:  = 5028 cm-1
3. a) Calcule o número de onda da vibração fundamental da molécula de H35Cl, sabendo que
a constante de força é igual a 516 Nm-1. R:  = 2991 cm-1
b) Calcule o desvio no número de onda quando se utiliza o isótopo 2H35Cl. As massas
relativas de H, D e 35Cl são, respectivamente, 1.008, 2.014 e 34.069. R:  = 847 cm-1
4. O espectro de rotação pura do iodeto de hidrogénio, H127I, consiste numa série de linhas
sucessivas afastadas de 13.10 cm-1.
a) Diga qual é o modelo geralmente utilizado para traduzir a rotação dos átomos de uma
molécula diatómica. Com base neste modelo, deduza a expressão da energia rotacional, EJ,
para a molécula diatómica.
b) Calcule a distância internuclear de equilíbrio da molécula H127I. R: r0 = 160.6 pm
c) Determine a constante rotacional de equilíbrio, B, para a molécula H127I. (Nota: admita
que B é independente do número quântico v). R: B = 1.297 10-22 J
Mestrado em Física e Química, ano lectivo 2005/6
2
5. Encontra-se representado na Figura 1 o diagrama dos quatro primeiros níveis de energia
rotacionais dos dois estados vibracionais v = 0 e v = 1 da molécula 1H35Cl, bem como a
estrutura rotacional da banda fundamental de absorção de roto-vibração centrada a 2886 cm-1.
a) Diga qual é o modelo geralmente utilizado para traduzir a vibração dos átomos de uma
molécula diatómica. Com base neste modelo, deduza a expressão da energia vibracional, Ev,
para a molécula diatómica.
b) Calcule o número de onda da vibração fundamental da molécula 1H35Cl, sabendo que a
constante de força da molécula é igual a 516 Nm-1. R:  = 2990 cm-1
c) Defina anarmonicidade e diga qual a sua influência na energia vibracional de uma
molécula diatómica. Determine a constante de anarmonicidade, xe, da molécula 1H35Cl.
R: xe = 55.9 cm-1
d) Diga qual é o modelo geralmente utilizado para traduzir a rotação dos átomos de uma
molécula diatómica. Com base neste modelo, deduza a expressão da energia rotacional, EJ,
para a molécula diatómica.
e) Determine a constante rotacional de equilíbrio, , para a molécula 1H35Cl, sabendo que
a distância internuclear de equilíbrio desta é igual a 1.275 Å. (Nota: admita que B é
independente do número quântico v). R: = 10.61 cm-1
f) Calcule o espaçamento entre as riscas sucessivas da banda de absorção fundamental.
 = 21.2 cm-1
g) Atribua o número quântico rotacional adequado a cada um dos oito níveis rotacionais
patentes no diagrama de níveis de energia patente na Figura 1 e calcule a energia rotacional
correspondente a cada um deles.
h) Trace linhas verticais no diagrama de níveis de energia patente na Figura 1 de modo a
representar as transições que dão origem à estrutura rotacional da banda de absorção
fundamental. Identifique os ramos P, R e Q no espectro de riscas presente na mesma Figura.
R:

Figura 1 - Diagrama de níveis de energia de uma molécula diatómica para os dois primeiros
Mestrado em Física e Química, ano lectivo 2005/6
3
níveis vibracionais e estrutura rotacional da banda de absorção fundamental
6. Os haletos de hidrogénio apresentam as seguintes frequências fundamentais de vibração:
H19F
H35Cl
H81Br
H127I
4141.3 cm-1
2988.9 cm-1
2649.7 cm-1
2309.5 cm-1
a) Diga qual é o modelo geralmente utilizado para traduzir a vibração dos átomos de uma
molécula diatómica. Com base neste modelo, deduza a expressão da energia vibracional, Ev,
para a molécula diatómica.
b) Calcule as constantes de força das ligações hidrogénio-haleto em cada caso.
R: 967.1, 515.6, 411.8 e 314.2 Nm-1.
c) Defina anarmonicidade e diga qual a sua influência na energia vibracional de uma
molécula diatómica.
7. O espectro de microondas da molécula 12C14N consiste numa série de linhas sucessivas
afastadas de 3.7978 cm-1.
a) Diga qual é o modelo geralmente utilizado para traduzir a rotação dos átomos de uma
molécula diatómica. Com base neste modelo, deduza a expressão da energia rotacional, EJ,
para a molécula diatómica.
b) Calcule a distância internuclear de equilíbrio da molécula 12C14N.
c) Determine a constante rotacional de equilíbrio, B, para a molécula 12C14N. (Nota:
admita que B é independente do número quântico v).
d) Diga qual é o modelo geralmente utilizado para traduzir a vibração dos átomos de uma
molécula diatómica. Com base neste modelo, deduza a expressão da energia vibracional, Ev,
para a molécula diatómica.
e) Calcule as constantes de força para o estiramento das ligações nas moléculas CN e CN+,
sabendo que os números de onda da vibração fundamental de cada uma destas moléculas são
iguais a 2068.61 cm-1 e 1580.00 cm-1, respectivamente. Comente o resultado obtido.
f) Defina anarmonicidade e diga qual a sua influência na energia vibracional de uma
molécula diatómica.
Mestrado em Física e Química, ano lectivo 2005/6
4
8. Apresentam-se a seguir algumas transições rotacionais puras do espectro de micro-ondas da
molécula de 12C16O no estado fundamental.
J  J+1
01
1 2
2 3
3 4
4 5
 (GHz)
115.271
230.538
345.796
461.041
576.268
a) Diga qual é o modelo geralmente utilizado para traduzir a rotação dos átomos de uma
molécula diatómica. Com base neste modelo, deduza a expressão da energia rotacional, EJ,
para a molécula diatómica.
b) Calcule a distância internuclear de equilíbrio, r0, da molécula 12C16O.
R: r0 = 1.131
10-10 m
c) Idealmente o espectro rotacional puro de uma molécula diatómica é constituído por uma
série de riscas igualmente espaçadas. Justifique esta afirmação, apresentando um esboço
ilustrativo.
d) Apresente uma razão para o facto do espaçamento entre riscas sucessivas não ser
constante no espectro rotacional da molécula 12C16O.
e) Sabendo que para a molécula 13C16O a transição rotacional pura J = 0  1 ocorre a
110.201 GHz, determine a massa atómica relativa do 13C. R: m13C = 12.9862
9. A frequência fundamental de vibração da molécula 1H127I ocorre a 2309.5 cm-1. A
constante rotacional desta molécula é igual a 6.551 cm-1. A distância internuclear de
equilíbrio eleva-se a 160.4 pm.
a) Diga qual é o modelo geralmente utilizado para traduzir a vibração dos átomos de uma
molécula diatómica. Com base neste modelo, deduza a expressão da energia vibracional, Ev,
para uma molécula diatómica.
b) Calcule o espaçamento entre as riscas sucessivas do espectro de roto-vibração do
1H127I. R: = 13.102 cm-1
c) Determine a massa atómica relativa do 127I. R: m127I = 129.0735
d) Calcule a constante de força da ligação hidrogénio-haleto. R: k = 313.2 Nm-1
e) Determine a posição da banda fundamental de absorção do espectro de roto-vibração do
1H127I. R:  = 2309.5 cm-1
Mestrado em Física e Química, ano lectivo 2005/6
CONSTANTES
h = 6.625 10-34 J s
c = 2.99 1010 cm s-1
me = 9.10956 10-31 kg
massa atómica relativa 1H = 1.007825
massa atómica relativa 14N = 14.003074
massa atómica relativa 19F = 18.998403
massa atómica relativa 35Cl = 34.968853
massa atómica relativa 79Br = 78.918340
massa atómica relativa 81Br = 90.916290
massa atómica relativa 127I = 126.904470
FACTORES DE CONVERSÃO
1 nm = 10-7 cm
1 Å = 10-8 cm
1 J = 107 erg
1 eV = 1.602 10-19 J
5