movimento retilíneo uniforme (mru) - Cursinho PET

MOVIMENTO RETILÍNEO UNIFORME
(MRU)
INTRODUÇÃO
A partir de agora passaremos a discutir tipos de movimentos e começaremos pelo
Movimento Retilíneo Uniforme. Este tipo de movimento de define por variações de
espaços iguais em intervalos de tempo iguais, em outras palavras a velocidade é
constante.
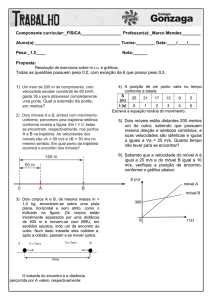
Observe no nosso exemplo que o rapaz percorre espaços iguais em tempos iguais. Ele
leva 2 s para percorrer cada 10 m, ou seja, quando está a 10 m se passaram 2 s, quando
está em 20 m se passaram 4 s e assim sucessivamente, de tal forma que se calcularmos
sua velocidade em cada uma das posições descritas (comparadas com a posição inicial),
teremos:
vm =
∆s
10
20
30
40
=
=
=
=
= 5 m/s
∆t
2
4
6
8
Portanto quando falamos de MRU não tem mais sentido em utilizarmos o conceito de
velocidade média, já que a velocidade não se altera no decorrer do movimento, logo
passaremos a utilizar:
v = vm
FUNÇÃO HORÁRIA DO MRU
A função horária de um movimento, representa o endereço de um móvel no tempo,
ou seja, ela fornece a posição desse móvel num instante qualquer. Com ela seremos
capazes de prever tanto posições futuras do movimento, como conhecer posições em que
o móvel já passou.
A seguir deduziremos a função s = f (t) para o MRU e como ponto de partida
utilizaremos a definição de velocidade.
Observe o esquema abaixo:
• O móvel parte de uma posição inicial so no instante t = 0;
• Num instante t qualquer ele estará na posição s.
Partindo da definição da velocidade:
Aplicando as observações descritas
acima, temos:
v =
s −s
∆s
= 2 1
∆t
t 2 − t1
v=
s − so
t−0
Simplificando a expressão, temos que:
v. t = s − s o
Isolando o espaço s, fica:
s o + v. t = s
Portanto a Função Horária do MRU é
dada por:
S = So + v.t
EXERCÍCIOS
1) Um móvel descreve um movimento retilíneo uniforme, de acordo com a função horária:
S = -20 + 5t (SI)
Para esse móvel determine:
(a) o espaço inicial e sua velocidade escalar;
(b) a posição no instante t = 10s;
(c) o instante em que ele passará pela origem dos espaços.
2) Um trem de 100m de comprimento, a uma velocidade constante de 10 m/s demora 1
min para atravessar uma ponte. Determine o comprimento da ponte.
3) Dois carros, A e B, se deslocam numa pista retilínea, ambos no mesmo sentido e com
velocidades constantes. O carro que está na frente desenvolve 72 km/h e o que está atrás
desenvolve 126 km/h. Num certo instante, a distância entre eles é de 225 m.
(a) Quanto tempo o carro A gasta para alcançar o carro B ?
(b) Que distância o carro que está atrás precisa percorrer para alcançar o que está na
frente ?
4) Duas estações A e B estão separadas por 200 km, medidos ao longo da trajetória. Pela
estação A passa um trem P, no sentido de A para B, e simultaneamente passa por B um
trem Q, no sentido de B para A. Os trens P e Q têm movimentos retilíneos e uniformes
com velocidades de valores absolutos 70 km/h e 30 km/h, respectivamente. Determine o
instante e a posição do encontro.
DESAFIO:
De duas cidadezinhas, ligadas por uma estrada reta de
10 km de comprimento, partem simultaneamente, uma
em direção à outra, duas carroças, puxadas cada uma
por um cavalo e andando à velocidade de 5 km/h. No
instante da partida, uma mosca, que estava pousada na
testa do primeiro cavalo, parte voando em linha reta,
com velocidade de 15 km/h e vai pousar na testa do
segundo cavalo. Após intervalo de tempo desprezível,
parte novamente e volta, com a mesma velocidade de
antes, em direção ao primeiro cavalo até pousar em sua
testa. E assim prossegue nesse vaivém, até que os dois
cavalos se encontram e a mosca morre esmagada entre
as duas testas. Quantos quilômetros percorreu a
mosca ?
GRÁFICOS DO MRU
A utilização de gráficos é uma poderosa arma para interpretação de dados. Os
gráficos são utilizados, por exemplo, em geografia para mostrar a evolução da densidade
populacional de uma região, na política afim de mostrar a corrida eleitoral, ou seja, o
posicionamento dos candidatos na disputa de um cargo político e também na matemática
mostrando desde funções simples a funções complexas.
Em física, utilizaremos os gráficos para mostrar a evolução no tempo de grandezas
como espaço, velocidade e aceleração.
GRÁFICOS DO ESPAÇO EM FUNÇÃO DO TEMPO (s x t)
No MRU, temos a seguinte função horária (s = f (t)):
S = So + v.t
Como esta função é do 1o grau, podemos ter os seguintes gráficos s x t para o MRU:
MOVIMENTO PROGRESSIVO
MOVIMENTO RETRÓGRADO
GRÁFICOS DA VELOCIDADE EM FUNÇÃO DO TEMPO (v x t)
Para o MRU, a velocidade é constante e diferente de zero. Nesse caso a função será uma
reta paralela ao eixo dos tempos.
MOVIMENTO PROGRESSIVO
MOVIMENTO RETRÓGRADO
GRÁFICOS DA ACELERAÇÃO EM FUNÇÃO DO TEMPO (a x t)
No MRU a aceleração é igual a zero e portanto teremos:
PROPRIEDADES NOS GRÁFICOS DO MRU
No gráfico s x t, no MRU temos:
A definição de tangente:
Aplicando a definição de tangente
no nosso caso, temos:
Sabendo que v =
∆s
, temos então:
∆t
tg θ =
cateto oposto
cateto adjacente
tg θ =
∆s
∆t
V = tg θ
No gráfico v x t, no MRU temos:
A área de um retângulo:
A = B.h
Aplicando em nosso caso, temos:
A = ∆t . v
Sabendo que v. ∆t = ∆s , teremos então:
ΔS = A
EXERCÍCIOS
5) Um móvel se desloca segundo o diagrama da figura.
Determine:
(a) a função horária do movimento;
(b) a posição do móvel no instante t = 30 s;
6) O diagrama horário representa o comportamento da
velocidade escalar de um móvel em função do tempo. No
instante t = 0, o móvel encontra-se na posição so = 3 m.
(a) Determine o deslocamento do corpo nos primeiros 10 s.
(b) Escreva a função horária para o espaço escalar.
(c) Determine o espaço do corpo após 10 s do início do
movimento.
(d) Construa um esboço do gráfico s x t deste movimento.
EXERCÍCIOS
COMPLEMENTARES
7) Durante uma tempestade, um indivíduo vê um relâmpago, mas ouve o trovão 5 s
depois. Considerando-se o som no ar, com velocidade praticamente constante e igual a
340 m/s determine:
(a) a distância que separa o indivíduo e o local do relâmpago;
(b) o tempo que a luz levou para ir do local onde foi produzido o relâmpago até onde está
o indivíduo. A velocidade da luz é aproximadamente 300 000 km/s.
8) Um atirador aponta para um alvo e dispara um projétil. Este sai da arma com
velocidade de 300 m/s. O impacto do projétil no alvo é ouvido pelo atirador 3,2 s após o
disparo. Sendo 340 m/s a velocidade de propagação do som no ar, calcule a distância do
atirador ao alvo.
(FUVEST-SP) 9) Uma composição ferroviária (19 vagões e uma locomotiva) desloca-se a
20 m/s. Sendo o comprimento de cada elemento da composição 10 m, qual é o tempo
que o trem gasta para ultrapassar:
(a) um sinaleiro ?
(b) uma ponte de 100 m de comprimento ?
(Mackenzie-SP) 10) Uma partícula está em movimento
retilíneo e suas posições variam com o tempo de acordo
com o gráfico ao lado. No instante t = 1,0 minuto, sua
posição será:
(a) 5,0 m;
(d) 300 m;
(b) 12 m;
(e) 1.200 m.
(c) 20 m;
(PUC-RJ) 11) O gráfico relaciona a posição (s) de um móvel
em função do tempo (t). A partir do gráfico pode-se concluir
corretamente que:
(a) o móvel inverte o sentido do movimento no instante t = 5
s;
(b) a velocidade é nula no instante t = 5 s;
(c) o deslocamento é nulo no intervalo de 0 a 5 s;
(d) a velocidade é constante e vale 20 m/s;
(e) a velocidade vale – 2 m/s no intervalo de 0 a 5 s e 2 m/s
no intervalo de 5 a 10 s.
GABARITO Exercícios e Exercícios Complementares
1)
(a) S0 = -20m e
V=5m/s
(b) 30m
(c) 4s
2) 500 m
3)
(a) 15s
(b) 525 m
5)
(a) s = 20 - 2.t
(b) s = -40 m
9)
(a) 10 s
(b) 15 s
6)
(a) ∆ s = 50 m
(b) s = 3 + 5.t
(c) s = 53 m
(d)
10) letra e
4) 2h e 140 km
7)
(a) 1700 m
(b) ≅ 5,67 . 10-6 s
8) 510 m
11) letra d