Força magnética em contatores

Força magnética em contatores
Antônio Flavio Licarião Nogueira
Universidade do Estado de Santa Catarina
[email protected]
1. O contator cc
Os contatores CC são formados por um circuito
magnético que contém uma parte móvel,
conforme ilustração da Fig. 1. Quando uma
corrente contínua alimenta a bobina B, a parte
móvel P é puxada para cima, fazendo com que
contatos elétricos C sejam fechados. Quando a
corrente se anula, a mola M faz com que a parte
móvel P volte ao seu local de repouso e os
contatos abrem.
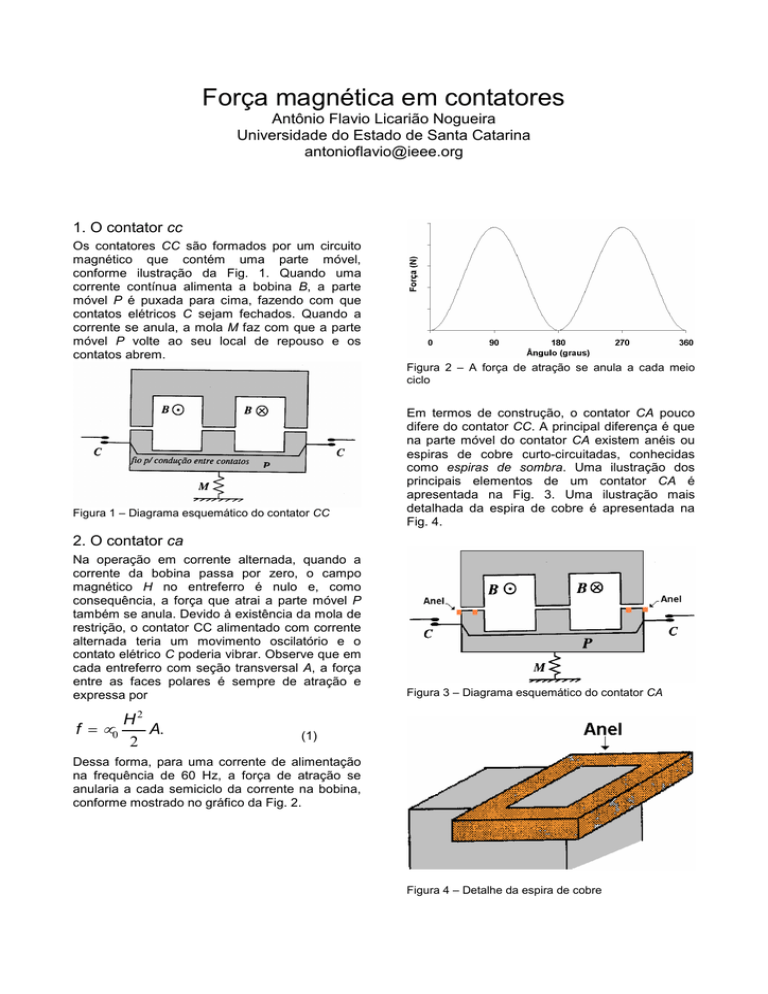
Figura 2 – A força de atração se anula a cada meio
ciclo
Figura 1 – Diagrama esquemático do contator CC
Em termos de construção, o contator CA pouco
difere do contator CC. A principal diferença é que
na parte móvel do contator CA existem anéis ou
espiras de cobre curto-circuitadas, conhecidas
como espiras de sombra. Uma ilustração dos
principais elementos de um contator CA é
apresentada na Fig. 3. Uma ilustração mais
detalhada da espira de cobre é apresentada na
Fig. 4.
2. O contator ca
Na operação em corrente alternada, quando a
corrente da bobina passa por zero, o campo
magnético H no entreferro é nulo e, como
consequência, a força que atrai a parte móvel P
também se anula. Devido à existência da mola de
restrição, o contator CC alimentado com corrente
alternada teria um movimento oscilatório e o
contato elétrico C poderia vibrar. Observe que em
cada entreferro com seção transversal A, a força
entre as faces polares é sempre de atração e
expressa por
f = µ0
H2
A.
2
Figura 3 – Diagrama esquemático do contator CA
(1)
Dessa forma, para uma corrente de alimentação
na frequência de 60 Hz, a força de atração se
anularia a cada semiciclo da corrente na bobina,
conforme mostrado no gráfico da Fig. 2.
Figura 4 – Detalhe da espira de cobre
Se a corrente de alimentação é senoidal, o fluxo
que circula no circuito magnético também o é. O
anel de cobre é, pois, atravessado por esse fluxo
variável no tempo e, em consequência, uma
corrente é induzida no mesmo. Essa corrente é
defasada de aproximadamente 90º do fluxo que a
cria. Assim, quando a corrente da bobina é nula,
a corrente no anel é máxima, fazendo com que
certa quantidade de fluxo – e também uma força
de atração – sejam mantidas no circuito
magnético. Como resultado final, a peça móvel P
se mantém atraída.
quase todas as linhas de campo – e fluxo
magnético – atravessam o interior do anel. Essa
corrente induzida mantém um fluxo circulando no
circuito magnético e uma força de atração entre
as duas partes do núcleo.
3. Análise das variáveis eletromagnéticas
Os principais elementos do modelo numérico para
análise de um contator ca são mostrados na Fig.
5. Nessa primeira análise vamos considerar que o
contator está aberto, ou seja, as duas partes que
compõem o núcleo magnético estão separadas
por uma camada de ar conhecida como
entreferro.
Figura 7 – Corrente somente no anel
Para esse contator, em particular, as variações
temporais das correntes são:
Ibobina = 350,0 sin(ϖt )
(2)
I anel = −4,02 cos(ϖt ).
(3)
O gráfico que representa a variação temporal
dessas correntes ao longo da metade do ciclo CA
é apresentado na Fig. 8. A representação fasorial
das correntes é mostrada na Fig. 9.
Figura 5 – Elementos do modelo numérico
Os traçados das equipotenciais do contator em
duas situações distintas são apresentados nas
figuras 6 e 7. Trata-se dos resultados de duas
análises magnetostáticas feitas no simulador de
campos FEMM [2]. A ilustração da Fig. 6
corresponde ao instante onde a corrente da
bobina é máxima.
Nessa situação, o fluxo
atravessa a região da espira de cobre sem
qualquer reação pois, nessa primeira simulação,
a corrente da espira é feita igual a zero.
Figura 8 – Variação temporal das correntes
Figura 6 – Corrente somente na bobina de campo
Na situação da Fig. 7, a corrente na bobina é nula
e a corrente nas espiras laterais é máxima. O
fluxo que circula no circuito magnético é criado
unicamente pela corrente que circula nas espiras.
Vale observar no traçado das equipotenciais que
Figura 9 – Representação fasorial das correntes.
Referências
4. Exercício
O circuito magnético de um contator ca é
apresentado na Fig. 1. O dispositivo opera na
frequência de 60 Hz e os detalhes geométricos da
espira de sombra são mostrados na Fig. 2.
Figura 1 – Contator ca
Figura 2 – Espira; dimensões em milímetros
Nessa análise, vamos considerar que o contator
está aberto e que o comprimento dos entreferros
é 1,5 mm. A corrente da bobina pode ser
expressa por
I bobina = 350 sin( wt ) A.
(a) Determine as expressões para a variação
temporal dos campos h e b;
(b) A superfície de ferro envolvida pela espira de
sombra tem uma área de 4 mm x 10 mm. Calcule
a expressão para o fluxo magnético φa que
atravessa a espira.
(c) Calcule a f.e.m. induzida na espira de cobre
empregando a lei de Faraday,
e(t ) = −
dφ a
.
dt
(d) Calcule a resistência Ra da espira de sombra.
Observe que sua geometria é retangular com
2
seção transversal de 1,0 mm .
(e) Para calcular a expressão para a corrente
induzida Ia, use a lei de Ohm,
I a (t ) =
e(t )
Ra
[1] J.P.A. Bastos, Eletromagnetismo para engenharia:
estática e quase-estática, Editora da UFSC,
Florianópolis, 2004, 1ª ed, p. 321-325.
[2] D. Meeker, FEMM 4.0 Magnetics and Electrostatics
Reference Manual, 2008.
Disponível em http://foster-miller.net/wiki/HomePage