Revisão-Julho-2016

Cinemática
1. O número de bactérias em uma cultura
cresce de modo análogo ao deslocamento de
uma partícula em movimento uniformemente
acelerado com velocidade inicial nula. Assim,
pode-se afirmar que a taxa de crescimento de
bactérias comporta-se da mesma maneira que
a velocidade de uma partícula.
Admita um experimento no qual foi medido o
crescimento do número de bactérias em um
meio adequado de cultura, durante um
determinado período de tempo. Ao fim das
primeiras quatro horas do experimento, o
5
número de bactérias era igual a 8  10 .
Após a primeira hora, a taxa de crescimento
dessa amostra, em número de bactérias por
hora, foi igual a:
5
a) 1,0  10
b)
5
2,0  10
4,0  10
d)
8,0  105
2.
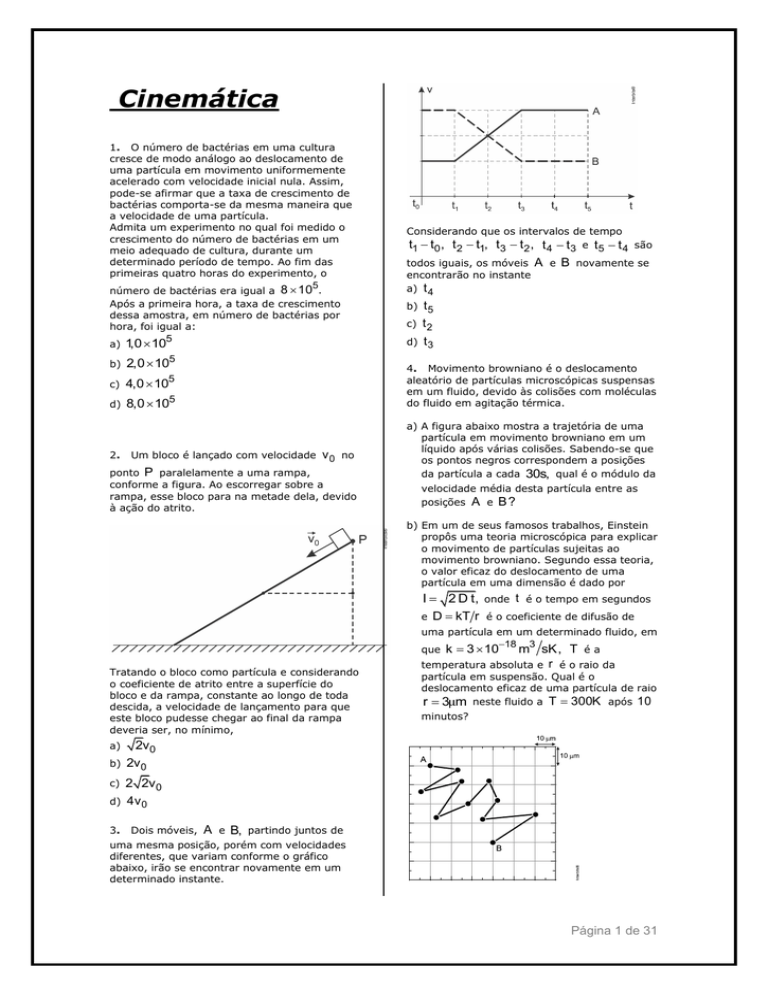
todos iguais, os móveis
encontrarão no instante
a) t 4
A e B novamente se
b) t 5
c) t 2
d) t 3
4. Movimento browniano é o deslocamento
aleatório de partículas microscópicas suspensas
em um fluido, devido às colisões com moléculas
do fluido em agitação térmica.
5
c)
Considerando que os intervalos de tempo
t1  t0 , t2  t1, t3  t 2 , t 4  t3 e t5  t 4 são
Um bloco é lançado com velocidade
v 0 no
ponto P paralelamente a uma rampa,
conforme a figura. Ao escorregar sobre a
rampa, esse bloco para na metade dela, devido
à ação do atrito.
a) A figura abaixo mostra a trajetória de uma
partícula em movimento browniano em um
líquido após várias colisões. Sabendo-se que
os pontos negros correspondem a posições
da partícula a cada 30s, qual é o módulo da
velocidade média desta partícula entre as
posições A e B ?
b) Em um de seus famosos trabalhos, Einstein
propôs uma teoria microscópica para explicar
o movimento de partículas sujeitas ao
movimento browniano. Segundo essa teoria,
o valor eficaz do deslocamento de uma
partícula em uma dimensão é dado por
I  2 D t,
e D  kT r
onde
t é o tempo em segundos
é o coeficiente de difusão de
uma partícula em um determinado fluido, em
18 3
que k  3  10
m sK, T é a
Tratando o bloco como partícula e considerando
o coeficiente de atrito entre a superfície do
bloco e da rampa, constante ao longo de toda
descida, a velocidade de lançamento para que
este bloco pudesse chegar ao final da rampa
deveria ser, no mínimo,
a)
b)
c)
d)
3.
temperatura absoluta e r é o raio da
partícula em suspensão. Qual é o
deslocamento eficaz de uma partícula de raio
r  3μm neste fluido a T  300K após 10
minutos?
2v0
2v0
2 2v0
4v 0
Dois móveis,
A e B, partindo juntos de
uma mesma posição, porém com velocidades
diferentes, que variam conforme o gráfico
abaixo, irão se encontrar novamente em um
determinado instante.
Página 1 de 31
5. Alguns meios de transporte são realmente
especiais como o veículo chamado Fênix 2, uma
cápsula de aço criada para resgatar, um a um,
33 mineiros chilenos que ficaram presos a
chegasse meia hora antes do horário
combinado.
700 metros abaixo da superfície.
Primeiramente foi perfurado um túnel até a
câmara onde se encontravam os mineiros. Em
seguida, a Fênix 2 foi levada até essa câmara.
Lá embaixo, a partir do instante em que um
mineiro já estava posicionado dentro da
cápsula, a subida da Fênix 2 pelo túnel
demorava 16 minutos.
É correto afirmar que, durante a subida da
cápsula da câmara até a superfície, a
velocidade média da Fênix 2 foi,
aproximadamente,
a) 0,7 km h.
b)
2,6 km h.
c) 3,4 km h.
d) 3,6 km h.
e) 4,4 km h.
6. A velocidade é uma grandeza que relaciona
a distância percorrida e o tempo gasto para
percorrê-la. A aceleração é uma grandeza que
mede a rapidez com que a velocidade varia.
Mais rápido, mais lento, são percepções
sensoriais. Tentamos medir com relógios tais
variações e nos rebelamos, quando elas não
concordam com a nossa percepção. Dizemos
nunca com muita facilidade, dizemos sempre
com muita facilidade, como se fôssemos fiéis a
um momento. “Mas o outro já está olhando
para o lado.” (LUFT, 2014)
O que é constante e imutável num momento
não será mais no momento seguinte. Uma
velocidade, num momento, pode não ser a
mesma num momento seguinte.
Assinale a situação em que o móvel apresenta
maior valor (positivo ou negativo) de
aceleração:
a) O móvel estava a 50m / s e manteve essa
velocidade durante
2,0 s.
b) O móvel estava a 20m / s e, em 10 s,
aumentou a sua velocidade para 40 m / s.
c) O móvel estava a 10m / s e, em 2,0 s,
diminuiu sua velocidade para zero.
d) O móvel estava a 40 m / s e, em 10 s,
diminuiu sua velocidade para zero.
7. João mora em São Paulo e tem um
compromisso às 16 h em São José dos
Campos, distante 90 km de São Paulo.
Pretendendo fazer uma viagem tranquila, saiu,
no dia do compromisso, de São Paulo às 14 h,
planejando chegar ao local pontualmente no
horário marcado. Durante o trajeto, depois de
ter percorrido um terço do percurso com
velocidade média de 45 km / h, João recebeu
Para chegar ao local do compromisso no novo
horário, desprezando- se o tempo parado para
atender a ligação, João deverá desenvolver, no
restante do percurso, uma velocidade média,
em km / h, no mínimo, igual a
a)
120.
60.
c) 108.
d) 72.
e) 90.
b)
8. Dois amigos, Tiago e João, resolvem iniciar
a prática de exercícios físicos a fim de melhorar
o condicionamento. Tiago escolhe uma
caminhada, sempre com velocidade escalar
constante de 0,875m / s, 300m na direção
norte e, em seguida,
400m na direção leste.
João prefere uma leve corrida, 800m na
direção oeste e, em seguida, 600m na direção
sul, realizando o percurso com velocidade
média de módulo 1,25m / s. Eles partem
simultaneamente do mesmo ponto.
De acordo com o exposto acima, é CORRETO
afirmar que:
01) o módulo da velocidade média de Tiago é
0,625m / s.
02) Tiago e João realizam seus percursos em
tempos diferentes.
04) o deslocamento de Tiago é de 700m.
08) a velocidade escalar média de João é de
1,75m / s.
16) o módulo do deslocamento de João em
relação a Tiago é 1500m.
32) a velocidade de João em relação a Tiago é
de 0,625m / s.
9. Uma bola é lançada com velocidade
horizontal de 2,5 m / s do alto de um edifício e
alcança o solo a
5,0 m da base do mesmo.
Despreze efeitos de resistência do ar e indique,
em metros, a altura do edifício.
uma ligação em seu celular pedindo que ele
Página 2 de 31
Considere:
g  10 m / s2
a)
10
2,0
c) 7,5
d) 20
e) 12,5
b)
10. Um carro, partindo do repouso, desloca-se
em um trecho A de modo que sua velocidade
aumente linearmente com o tempo até atingir
60km h. Após algum tempo, em um trecho B,
o motorista aciona o freio, de modo que a
velocidade decresça também linearmente com o
tempo. Considere que a trajetória do automóvel
é retilínea nos dois trechos e que ambos sejam
estradas sem aclives ou declives. Assim, podese afirmar corretamente que o vetor aceleração
nos dois trechos tem
a) mesma direção e mesmo sentido.
b) mesma direção e sentido contrário.
c) mesmo módulo e mesmo sentido.
d) direções perpendiculares e mesmo módulo.
Sabendo que o encontro entre elas ocorre,
apenas, uma vez, o valor da separação inicial,
d, entre as partículas vale
a)
4m
b) 8 m
c) 16 m
d) 96 m
e) 192 m
14. Considere o gráfico abaixo, que representa
a velocidade de um corpo em movimento
retilíneo em função do tempo, e as afirmativas
que seguem.
11. Um trem, durante os primeiros minutos de
sua partida, tem o módulo de sua velocidade
dado por v  2t, onde t é o tempo em
segundos e
v a velocidade, em m s.
Considerando que um dos vagões pese
3  103 kg, qual o módulo da força resultante
sobre esse vagão, em newtons?
a) 3000.
1,0 m / s2 .
II. A distância percorrida nos 10 s é de 50 m.
b) 6000.
I. A aceleração do móvel é de
c) 1500.
d) 30000.
12. A Agência Espacial Brasileira está
desenvolvendo um veículo lançador de satélites
(VLS) com a finalidade de colocar satélites em
órbita ao redor da Terra. A agência pretende
lançar o VLS em 2016, a partir do Centro de
Lançamento de Alcântara, no Maranhão.
a) Considere que, durante um lançamento, o
VLS percorre uma distância de 1200km em
800s. Qual é a velocidade média do VLS
nesse trecho?
b) Suponha que no primeiro estágio do
lançamento o VLS suba a partir do repouso
com aceleração resultante constante de
módulo aR . Considerando que o primeiro
estágio dura
distância de
13.
80s, e que o VLS percorre uma
32km, calcule aR .
Duas partículas,
1
e
2,
se movem ao
longo de uma linha horizontal, em rota de
encontro com velocidades iniciais de módulos
iguais a v1  10m / s e v 2  14 m / s e
acelerações contrárias às suas velocidades de
2
2
módulos a1  1,0m / s e a2  0,5m / s .
III. A velocidade varia uniformemente, e o
móvel percorre 10 m a cada segundo.
IV. A aceleração é constante, e a velocidade
aumenta 10 m / s a cada segundo.
São verdadeiras apenas as afirmativas
a) I e II.
b) I e III.
c) II e IV.
d) I, III e IV.
e) II, III e IV.
15. Um ciclista está pedalando sua bicicleta
em um trecho retilíneo de uma ciclovia, em
uma famosa avenida de Florianópolis. No
instante t  0, a velocidade do ciclista é
18 km / h no sentido positivo da trajetória, isto
é, eixo
0x,
e sua posição é
20 m em relação a
uma parada de ônibus. A aceleração do ciclista
2
é ax  4,0 m / s . Considerando o conjunto
ciclista e bicicleta como um ponto material e
com massa de 70 kg, assinale a soma da(s)
proposição(ões) CORRETA(S).
01) O movimento da bicicleta é retilíneo e
uniforme.
02) A expressão matemática que define a
posição da bicicleta é
x  20  5t  4t 2.
Página 3 de 31
04) A força resultante a qual o conjunto está
sujeito é 280 N.
08) O trabalho total realizado sobre o conjunto,
no intervalo de tempo de 0 a 2s, foi de
3600 J.
16) A quantidade de movimento do conjunto no
instante 2 s foi de 910 kg  m / s.
32) O impulso sofrido pelo conjunto no
intervalo de tempo de 0 a 2 s foi de
910 Ns.
16. Uma criança com uma bola nas mãos está
sentada em um “gira‐gira” que roda com
velocidade angular constante e frequência
f  0,25 Hz.
a) Considerando que a distância da bola ao
centro do “gira‐gira” é 2 m, determine os
módulos da velocidade
b) a componente tangencial da aceleração
apresenta a mesma direção e o mesmo
sentido da velocidade.
c) o movimento do automóvel é circular
uniforme.
d) o movimento do automóvel é uniformemente
acelerado.
e) os vetores velocidade e aceleração são
perpendiculares entre si.
19. Um bote de assalto deve atravessar um rio
de largura igual a 800m, numa trajetória
perpendicular à sua margem, num intervalo de
tempo de 1 minuto e 40 segundos, com
velocidade constante.
Considerando o bote como uma partícula,
desprezando a resistência do ar e sendo
constante e igual a 6 m/s a velocidade da
correnteza do rio em relação à sua margem, o
módulo da velocidade do bote em relação à
água do rio deverá ser de:
V T e da aceleração
a da bola, em relação ao chão.
Num certo instante, a criança arremessa a bola
horizontalmente em direção ao centro do
“gira‐gira”, com velocidade
V R de módulo
4 m / s, em relação a si.
Determine, para um instante imediatamente
após o lançamento,
b) o módulo da velocidade U da bola em
relação ao chão;
c) o ângulo θ entre as direções das
velocidades
U e V R da bola.
Note e adote:
π3
17. Um avião, após deslocar-se 120 km para
nordeste (NE), desloca-se 160 km para sudeste
(SE). Sendo um quarto de hora, o tempo total
dessa viagem, o módulo da velocidade vetorial
média do avião, nesse tempo, foi de
a) 320 km/h
b) 480 km/h
c) 540 km/h
d) 640 km/h
e) 800 km/h
18. A figura a seguir apresenta, em dois
instantes, as velocidades v1 e v2 de um
automóvel que, em um plano horizontal, se
desloca numa pista circular.
Com base nos dados da figura, e sabendo-se
que os módulos dessas velocidades são tais que
v1>v2 é correto afirmar que
a) a componente centrípeta da aceleração é
diferente de zero.
a) 4 m/s
b) 6 m/s
c) 8 m/s
d) 10 m/s
e) 14 m/s
20. Considere um móvel que percorre a metade
de uma pista circular de raio igual a 10,0m em
10,0s. Adotando-se 2 como sendo 1,4 e π
igual a 3, é correto afirmar:
a) O espaço percorrido pelo móvel é igual a
60,0m.
b) O deslocamento vetorial do móvel tem
módulo igual a 10,0m.
c) A velocidade vetorial média do móvel tem
módulo igual a 2,0m/s.
d) O módulo da velocidade escalar média do
móvel é igual a 1,5m/s.
e) A velocidade vetorial média e a velocidade
escalar média do móvel têm a mesma
intensidade.
21. O estudo da física em duas e três
dimensões requer o uso de uma ferramenta
matemática conveniente e poderosa conhecida
como vetor. Sobre os vetores, assinale o que
for correto.
01) A direção de um vetor é dada pelo ângulo
que ele forma com um eixo de referência
qualquer dado.
02) O comprimento do segmento de reta
orientado que representa o vetor é
proporcional ao seu módulo.
04) Dois vetores são iguais somente se seus
módulos correspondentes forem iguais.
08) O módulo do vetor depende de sua direção
e nunca é negativo.
16) Suporte de um vetor é a reta sobre a qual
ele atua.
Página 4 de 31
TEXTO PARA A PRÓXIMA QUESTÃO:
Nesta prova adote os conceitos da Mecânica
Newtoniana e as seguintes convenções:
O valor da aceleração da gravidade: g = 10
m/s2.
O valor π = 3.
A resistência do ar pode ser desconsiderada.
22. Em uma competição de rally pelo interior
do Brasil, um dos competidores para o seu jeep
por falta de gasolina. O motorista então anda
200 metros em linha reta para a direita até
encontrar um posto de combustível. Em
seguida, ele anda mais 10 metros, no mesmo
sentido, até uma loja de conveniência para
comprar água. Finalmente, o motorista retorna
em linha reta para o seu jeep.
Considerando o posto de gasolina como origem
do sistema de referência e adotando o sentido
positivo como sendo o da esquerda para a
direita, identifique as afirmativas corretas:
(
) A posição do jeep em relação ao posto é
−200 m.
(
) O deslocamento do motorista entre o
posto e a loja de conveniência foi de 10
m.
(
) O deslocamento do motorista entre a loja
de conveniência e o jeep foi de −210 m.
(
) O deslocamento do motorista, no trajeto
posto de combustível - loja de
conveniência - posto de combustível, foi
de 20 m.
(
) A distância total percorrida pelo
motorista, para comprar gasolina e água
e retornar para o jeep, foi de 420 m.
23. De dentro de um automóvel em
movimento retilíneo uniforme, numa estrada
horizontal, um estudante olha pela janela
lateral e observa a chuva caindo, fazendo um
ângulo
sen
 
com a direção vertical, com
  = 0,8 e cos   = 0,6.
Para uma pessoa parada na estrada, a chuva
cai verticalmente, com velocidade constante de
módulo v. Se o velocímetro do automóvel
marca 80,0 km/h, pode-se concluir que o valor
de v é igual a:
a) 48,0 km/h
b) 60,0 km/h
c) 64,0 km/h
d) 80,0 km/h
e) 106,7 km/h
24. Um barco pode viajar a uma velocidade de
11 km/h em um lago em que a água está
parada. Em um rio, o barco pode manter a
mesma velocidade com relaçăo à água. Se esse
barco viaja no Rio Săo Francisco, cuja
velocidade da água, em relaçăo à margem,
assume-se 0,83 m/s, qual é sua velocidade
aproximada em relaçăo a uma árvore plantada
na beira do rio quando seu movimento é no
sentido da correnteza e contra a correnteza,
respectivamente?
a) 14 km/h e 8 km/h.
b) 10,2 m/s e 11,8 m/s.
c) 8 km/h e 14 km/h.
d) 11,8 m/s e 10,2 m/s.
25. Um pequeno avião acelera, logo após a sua
decolagem, em linha reta, formando um ângulo
de 45o com o plano horizontal.
Sabendo que a componente horizontal de sua
aceleração é de 6,0 m/s2, calcule a componente
vertical da mesma.
(Considere g = 10 m/s2)
a) 6,0 m/s2
b) 4,0 m/s2
c) 16,0 m/s2
d) 12,0 m/s2
e) 3,0 m/s2
26. Toda vez que o vetor velocidade sofre
alguma variação, significa que existe uma
aceleração atuando. Existem a aceleração
tangencial ou linear e a aceleração centrípeta.
Assinale a alternativa correta que caracteriza
cada uma dessas duas acelerações.
a) Aceleração tangencial é consequência da
variação no módulo do vetor velocidade;
aceleração
centrípeta é consequência da variação na
direção do vetor velocidade.
b) Aceleração tangencial é consequência da
variação na direção do vetor velocidade;
aceleração
centrípeta é consequência da variação no
módulo do vetor velocidade.
c) Aceleração tangencial só aparece no MRUV;
aceleração centrípeta só aparece no MCU.
d) Aceleração tangencial tem sempre a mesma
direção e sentido do vetor velocidade;
aceleração
centrípeta é sempre perpendicular ao vetor
velocidade.
e) Aceleração centrípeta tem sempre a mesma
direção e sentido do vetor velocidade;
aceleração
tangencial é sempre perpendicular ao vetor
velocidade.
27. Um corpo move-se no plano XY, sendo as
coordenadas de sua posição dadas pelas
funções
x(t)  3t e y(t)  t3  12t , em
centímetros, com t em segundos. O módulo do
deslocamento entre os instantes t = 0 e t = 4
segundos, em centímetros, é
a) 4.
b) 20.
c) 38.
d) 48.
28. Uma ave marinha costuma mergulhar de
uma altura de 20 m para buscar alimento no
mar.
Suponha que um desses mergulhos tenha sido
feito em sentido vertical, a partir do repouso e
exclusivamente sob ação da força da gravidade.
Desprezando-se as forças de atrito e de
resistência do ar, a ave chegará à superfície do
mar a uma velocidade, em m/s,
aproximadamente igual a:
a) 20
b) 40
c) 60
d) 80
Página 5 de 31
29. A castanha-do-pará (Bertholletia excelsa)
é fonte de alimentação e renda das populações
tradicionais da Amazônia. Sua coleta é
realizada por extrativistas que percorrem
quilômetros de trilhas nas matas, durante o
período das chuvas amazônicas. A castanheira
é uma das maiores árvores da floresta,
atingindo facilmente a altura de 50m. O fruto
da castanheira, um ouriço, tem cerca de
1kg e
contém, em média, 16 sementes. Baseando-se
nesses dados e considerando o valor padrão da
2
aceleração da gravidade 9,81m / s , pode-se
Assinale a alternativa que representa o esboço
dos gráficos em relação à velocidade  tempo
e à aceleração  tempo, respectivamente.
estimar que a velocidade com que o ouriço
atinge o solo, ao cair do alto de uma
castanheira, é de, em m / s,
aproximadamente,
a) 5,2.
b)
c)
d)
e)
10,1.
20,4.
31,3.
98,1.
a)
30. Analise a situação a seguir.
Um jovem, desejando estimar a altura do
terraço onde se encontrava, deixou cair várias
esferas de aço e, munido de um cronômetro,
anotou o tempo de queda de todas. Após
alguns cálculos, elaborou o gráfico abaixo com
o tempo médio " t " gasto pelas esferas na
queda.
b)
Considere que, para facilitar os cálculos, o
jovem desprezou a resistência do ar o adotou
g  10 m / s2. Pode-se afirmar que: o valor
encontrado para o tempo médio
c)
(t) e a altura
do terraço foram, respectivamente:
a) 1,0s e 10m
b) 1,2s e 12m
c) 2,0s e 20m
d) 2,5s e 25m
e) 3,0s e 30m
31 Uma pessoa do alto de um prédio solta uma
bola e mede o módulo da posição da bola em
função do tempo. A figura, abaixo, mostra o
esboço do gráfico da posição em relação ao
tempo.
d)
Página 6 de 31
e)
32. Na Terra a aceleração da gravidade é
aproximadamente igual a 10 m/s2 e na Lua, 2
m/s2. Se um objeto for abandonado de uma
mesma altura em queda livre nos dois corpos
celestes, então a razão entre os tempos de
queda na Lua e na Terra é
a)
1/ 10.
b) 1/5.
c) 1.
d) 5.
e) 10.
33. Considere um vagão deslocando-se em
uma trajetória retilínea com velocidade
constante e igual a 5 m/s. Um observador, A,
dentro dele, lança uma pedra verticalmente
para cima. Um outro observador, B, do lado de
fora do vagão e em repouso em relação à
Terra, observa o vagão passar. Sendo VA e VB,
respectivamente, as velocidades da pedra no
ponto mais alto de sua trajetória em relação a
cada observador, pode-se concluir que:
a) VA = 0 e VB = 0
b) VA = 0 e VB = 5 m/s
c) VA = 5 m/s e VB = 0
d) VA = 5 m/s e VB = 5m/s
e) VA = 0 e VB = 10 m/s
34. Em um certo planeta, um corpo é atirado
verticalmente para cima, no vácuo, de um
ponto acima do solo horizontal. A altura, em
metros, atingida pelo corpo é dada pela função
h(t)  At 2  Bt  C, em que t está em
segundos. Decorridos 4 segundos do
lançamento, o corpo atinge a altura máxima de
9 metros e, 10 segundos após o lançamento, o
corpo toca o solo.
A altura do ponto de lançamento, em metros, é
a) 0
b) 2
c) 3
d) 5
e) 6
Estática
1. Considere que ambos os sistemas
mostrados nas Figuras (a) e (b) a seguir
estejam em equilíbrio e que as forças de tensão
nos fios esquerdos possuam intensidades iguais
a Ta e Tb, respectivamente.
Sabendo-se que M = 5,0 kg e que o ângulo
igual a 60°, é CORRETO afirmar que
1/2
a) Ta  2
Tb
1/2
b) Ta  3
Tb
1/2
c) Ta  5
Tb
θ é
 
 
 
Ta  Tb / 2
e) Ta  Tb
d)
2. Na figura abaixo, blocos idênticos estão
suspensos por cordas idênticas em três
situações distintas, (1), (2) e (3).
Assinale a alternativa que apresenta as
situações na ordem crescente de probabilidade
de rompimento das cordas. (O sinal de
igualdade abaixo indica situações com a mesma
probabilidade de rompimento).
a) (3), (2), (1).
b) (3), (2) = (1).
c) (1), (2), (3).
d) (1) = (2), (3).
e) (1) = (2) = (3).
3. Um bloco de 6 kg de massa é mantido em
repouso, encostado em uma parede vertical,
aplicando-se a ele uma força horizontal F . Se a
aceleração da gravidade vale 10 m/s2 e o
coeficiente de atrito estático entre o bloco e a
parede é 0,2, qual é o menor valor de
F , em
Newtons para que o bloco permaneça em
repouso?
a) 60
b) 120
c) 180
d) 240
e) 300
4. Uma pessoa, de massa 80,0 kg, consegue
aplicar uma força de tração máxima de 800,0
N. Um corpo de massa M necessita ser
levantado como indicado na figura a seguir. O
coeficiente de atrito estático entre a sola do
sapato da pessoa e o chão de concreto é
 e  1,0 .
Página 7 de 31
Faça um esboço de todas as forças que atuam
em todo o sistema e determine qual a maior
massa M que pode ser levantada pela pessoa
sem que esta deslize, para um ângulo
  45º .
b) 1,2; 0,5; 0,2.
c) 0,7; 0,3; 0,2.
d) 0,2; 0,5; 1,2.
e) 0,2; 0,3; 0,7.
7.
Três blocos de massas m1 , m2 e m3 ,
respectivamente, estão unidos por cordas de
massa desprezível, conforme mostrado na
figura. O sistema encontra-se em equilíbrio
estático. Considere que não há atrito no
movimento da roldana e que o bloco de massa
m1 está sobre uma superfície horizontal.
Assinale a alternativa que apresenta
corretamente (em função de m1 e m3 ) o
5. O sistema da figura é formado por um bloco
de 80 kg e duas molas de massas desprezíveis
associadas em paralelo, de mesma constante

elástica. A força horizontal F mantém o corpo
em equilíbrio estático, a deformação elástica do
sistema de molas é 20 cm e a aceleração da
gravidade local tem módulo 10 m/s2. Então, é
correto afirmar que a constante elástica de
cada mola vale, em N/cm:
a) 10
b) 20
c) 40
d) 60
e) 80
apoiado.
a)
m3
2m1
b)
m1
2m3
c)
d)
6. Um móbile pendurado no teto tem três
elefantezinhos presos um ao outro por fios,
como mostra a figura. As massas dos elefantes
de cima, do meio e de baixo são,
respectivamente, 20g, 30g e 70g. Os valores de
tensão, em newtons, nos fios superior, médio e
inferior são, respectivamente, iguais a
Note e adote: Desconsidere as massas dos
fios.
Aceleração da gravidade
coeficiente de atrito estático entre o bloco de
massa m1 e a superfície em que ele está
g  10 m/s2 .
e)
3m3
2m1
3m1
2m3
3m1
m3
8. A BR-101, também conhecida como
Rodovia Translitorânea, faz a ligação do Brasil
de norte a sul. Sua duplicação, portanto, é uma
obra de grande importância. A construção da
nova ponte de Laguna, batizada em
homenagem à lagunense Anita Garibaldi, a
heroína de dois mundos (América Latina e
Europa), faz parte da obra de duplicação dessa
rodovia e substituirá a atual ponte de Laguna, a
Ponte Henrique Lage, inaugurada em 1º de
setembro de 1934. A construção da nova ponte
de Laguna e a conclusão da duplicação da
rodovia BR-101 darão um grande impulso ao
desenvolvimento econômico desta região e,
também, ao turismo.
Disponível em: <www.pontedelaguna.com.br>
[Adaptado] Acesso em: 17 ago. 2014.
a) 1,2; 1,0; 0,7.
O desenho abaixo ilustra o sistema de
guindaste usado para suspender os blocos de
concreto que darão a base para a pista de
Página 8 de 31
rolamento dos veículos. Uma estrutura metálica
fica apoiada sobre dois pilares (A e C), dando
suporte ao guindaste que suspende os blocos
de concreto, para que sejam fixados aos
demais. Vamos admitir que a estrutura metálica
possua uma massa de 200 toneladas
(200  103 kg) cujo centro de massa esteja a
80,0 m do pilar A, que cada bloco possua
uma massa de 10 toneladas e que o guindaste
tenha uma massa de 5 toneladas. Adote
g  10m / s2 .
O centro de massa
(CM) do guindaste sem
carga está localizado na posição
(x  3 m, y  2 m). Na situação mostrada na
figura, a maior carga
pode levantar pesa
a) 7.000 N
P que esse guindaste
b)
50.000 N
75.000 N
d) 100.000 N
e) 150.000 N
10. A Op Art ou “arte óptica” é um segmento
do Cubismo abstrato que valoriza a ideia de
mais visualização e menos expressão. É por
esse motivo que alguns artistas dessa vertente
do Cubismo escolheram o móbile como base de
sua arte.
No móbile representado, considere que os
“passarinhos” tenham a mesma massa e que as
barras horizontais e os fios tenham massas
desprezíveis.
 M  0, assim como a soma das
forças,  F  0.
02) a altura do bloco suspenso pelo guindaste
influencia o seu torque em relação ao pilar
A ou ao pilar C.
04) à medida que o guindaste se desloca em
direção ao pilar B, a força de reação dos
pilares A e C aumenta e diminui,
respectivamente.
08) supondo que o bloco suspenso esteja a
20,0 m do pilar C, as forças de reação
nos pilares
A e C são, respectivamente,
121,5  10 N e 93,5  104 N.
4
16) inserir um novo ponto de sustentação da
estrutura no pilar B não altera as forças de
reação nos pilares A e C.
32) as forças de reação nos pilares A e C se
alteram durante a subida do bloco, em
velocidade constante, pelo guindaste.
9.
50.000 N
sem carga e os pontos de apoio de suas rodas
no solo horizontal estão em x  0 e x  5 m.
c)
Com base nos dados acima, é CORRETO afirmar
que:
01) para que todo o sistema (estrutura,
guindaste e bloco) esteja em equilíbrio, é
necessário que a soma dos momentos seja
zero,
O guindaste da figura acima pesa
Para que o móbile permaneça equilibrado,
conforme a figura, a barra maior que sustenta
todo o conjunto deve receber um fio que a
pendure, atado ao ponto numerado por
a) 1.
b) 2.
c) 3.
d)
e)
4.
5.
11. O tratamento de tração é a aplicação de
uma força de tração sobre uma parte do corpo.
A tração ainda é usada principalmente como
uma prescrição em curto prazo até que outras
modalidades, como a fixação externa ou
interna, sejam possíveis. Isso reduz o risco da
síndrome do desuso. Seja um paciente de
massa 50 kg submetido a um tratamento de
tração como na figura abaixo, que está deitado
em uma cama onde o coeficiente de atrito entre
a mesma e o paciente é μ  0,26.
Página 9 de 31
Sabendo-se que o ângulo entre a força de
tração e a horizontal é 30°, a alternativa
correta que apresenta a máxima massa, em
kg, que deve ser utilizada para produzir tal
força de tração sem que o paciente se desloque
em cima da cama é:
a) 25
b) 13
c) 10
d) 50
12.
b)
c)
d)
A figura acima mostra uma viga em equilíbrio.
Essa viga mede 4 m e seu peso é desprezível.
Sobre ela, há duas cargas concentradas, sendo
uma fixa e outra variável. A carga fixa de
20 kN está posicionada a 1 m do apoio A ,
14. O desenho abaixo mostra uma barra
homogênea e rígida “AB” de peso desprezível,
apoiada no ponto “O” do suporte.
enquanto a carga variável só pode se posicionar
entre a carga fixa e o apoio B. Para que as
reações verticais (de baixo para cima) dos
apoios A e B sejam iguais a 25 kN e
35 kN, respectivamente, a posição da carga
variável, em relação ao apoio B, e o seu
módulo devem ser
a) 1,0 m e 50 kN
b)
1,0 m e 40 kN
c) 1,5 m e 40 kN
d) 1,5 m e 50 kN
e) 2,0 m e 40 kN
13. A figura abaixo ilustra uma ferramenta
utilizada para apertar ou desapertar
determinadas peças metálicas.
A distância da extremidade “B” ao ponto de
apoio “O” é o triplo da distância de “A” a “O”.
No lado esquerdo, um fio ideal isolante e
inextensível, de massa desprezível, prende a
extremidade “A” da barra a uma carga elétrica
puntiforme positiva de módulo “Q”. A carga “Q”
está situada a uma distância “d” de uma outra
carga elétrica fixa puntiforme negativa de
módulo “q”.
No lado direito, um fio ideal inextensível e de
massa desprezível prende a extremidade “B” da
barra ao ponto “C”.
A intensidade da força de tração no fio “BC”,
para que seja mantido o equilíbrio estático da
barra na posição horizontal, é de:
Dados:
sen 30  cos 60  1 2
cos 30  sen 60  3 2
K 0 é a constante eletrostática do meio
Para apertar uma peça, aplicando-se a menor
intensidade de força possível, essa ferramenta
deve ser segurada de acordo com o esquema
indicado em:
a)
b)
c)
a)
d)
K 0Qq
2d2
K 0Qq
4d2
3 K 0 Qq
3d2
3 K 0 Qq
9d2
Página 10 de 31
e)
K 0Qq
15.
d2
Uma barra metálica homogênea, de
2,0 m de comprimento e 10 N de peso, está
presa por um cabo resistente. A barra mantém
dois blocos em equilíbrio, conforme mostra a
figura abaixo. Sendo d  0,5 m e o peso do
e) 600 N e 650 N
17. Em um parque de diversão, Carlos e
Isabela brincam em uma gangorra que dispõe
de dois lugares possíveis de se sentar nas suas
extremidades. As distâncias relativas ao ponto
de apoio (eixo) estão representadas conforme a
figura a seguir.
PA  100 N, é correto afirmar que o
peso do bloco B, em N, é:
bloco A,
a) 45
b) 30
c) 60
d) 6
e) 55
16. Um portão maciço e homogêneo de 1,60
m de largura e 1,80 m de comprimento,
pesando 800 N, está fixado em um muro por
meio das dobradiças “A”, situada a 0,10 m
abaixo do topo do portão, e “B”, situada a 0,10
m de sua parte inferior. A distância entre as
dobradiças é de 160 m, conforme o desenho
abaixo.
Sabendo-se que Carlos tem 70 kg de massa e
que a barra deve permanecer em equilíbrio
horizontal, assinale a alternativa correta que
indica respectivamente o tipo de alavanca da
gangorra e a massa de Isabela comparada com
a de Carlos.
a) Interfixa e maior que 70 kg.
b) Inter-resistente e menor que 70 kg.
c) Interpotente e igual a 70 kg.
d) Inter-resistente e igual a 70 kg.
e) Interfixa e menor que 70 kg.
18.
Um homem de massa igual a
80 kg está
em repouso e em equilíbrio sobre uma prancha
rígida de 2,0 m de comprimento, cuja massa é
muito menor que a do homem.
A prancha está posicionada horizontalmente
sobre dois apoios, A e B, em suas
extremidades, e o homem está a 0,2 m da
extremidade apoiada em A.
A intensidade da força, em newtons, que a
prancha exerce sobre o apoio A equivale a:
a) 200
b) 360
c) 400
d) 720
19. Deseja-se construir um móbile simples,
com fios de sustentação, hastes e pesinhos de
chumbo. Os fios e as hastes têm peso
desprezível. A configuração está demonstrada
na figura abaixo.
Elas têm peso e dimensões desprezíveis, e cada
dobradiça suporta uma força cujo módulo da
componente vertical é metade do peso do
portão.
Considerando que o portão está em equilíbrio, e
que o seu centro de gravidade está localizado
em seu centro geométrico, o módulo da
componente horizontal da força em cada
dobradiça “A” e “B” vale, respectivamente:
a) 130 N e 135 N
b) 135 N e 135 N
c) 400 N e 400 N
d) 450 N e 450 N
O pesinho de chumbo quadrado tem massa 30
g, e os pesinhos triangulares têm massa 10 g.
Para que a haste maior possa ficar horizontal,
qual deve ser a distância horizontal x, em
centímetros?
Página 11 de 31
a) 45
b) 15
c) 20
d) 10
e) 30
20.
mola deve se contrair de um valor máximo
d,
quando o elevador cai, a partir do repouso, de
uma altura h, como ilustrado na figura abaixo.
Uma barra homogênea de peso igual a
Para que a exigência do projetista seja
satisfeita, a mola a ser empregada deve ter
constante elástica dada por
50 N está em repouso na horizontal. Ela está
apoiada em seus extremos nos pontos A e B,
que estão distanciados de 2 m. Uma esfera Q
de peso
80 N é colocada sobre a barra, a uma
40 cm do ponto A, conforme
distância de
representado no desenho abaixo:
Note e adote:
- forças dissipativas devem ser ignoradas;
- a aceleração local da gravidade é g.
A intensidade da força de reação do apoio sobre
a barra no ponto B é de
a) 32 N
b) 41 N
c) 75 N
d) 82 N
e) 130 N
Conservação de
energia
1. (Fuvest) Uma criança de
a)
2 m g  h  d / d2
b)
2 m g  h  d  / d2
2 m g h / d2
d) m g h / d
c)
e)
m g/d
3. (Fuvest) A figura abaixo mostra o gráfico da
energia potencial gravitacional U de uma
esfera em uma pista, em função da
componente horizontal x da posição da esfera
na pista.
30 kg está em
repouso no topo de um escorregador plano de
2,5 m 2,5 m de altura, inclinado 30 em
relação ao chão horizontal. Num certo instante,
ela começa a deslizar e percorre todo o
escorregador.
Determine
a) a energia cinética E e o módulo Q da
quantidade de movimento da criança, na
metade do percurso;
b) o módulo F da força de contato entre a
criança e o escorregador;
c) o módulo a da aceleração da criança.
Note e adote:
Forças dissipativas devem ser ignoradas.
A aceleração local da gravidade é
10 m / s2 .
sen 30  cos 60  0,5
sen 60  cos 30  0,9
2. (Fuvest) No desenvolvimento do sistema
amortecedor de queda de um elevador de
massa m, o engenheiro projetista impõe que a
A esfera é colocada em repouso na pista, na
posição de abscissa x  x1, tendo energia
mecânica E  0. A partir dessa condição, sua
energia cinética tem valor
Note e adote:
- desconsidere efeitos dissipativos.
a) máximo igual a
b) igual a
E
U0 .
quando
x  x3 .
x  x2 .
d) máximo quando x  x3 .
e) máximo quando x  x 2 .
c) mínimo quando
Página 12 de 31
4. (Unifesp) Uma pista de esqui para
treinamento de principiantes foi projetada de
modo que, durante o trajeto, os esquiadores
não ficassem sujeitos a grandes acelerações
nem perdessem contato com nenhum ponto da
pista. A figura representa o perfil de um trecho
dessa pista, no qual o ponto C é o ponto mais
alto de um pequeno trecho circular de raio de
curvatura igual a 10 m.
e)
v0 
g
m
6. (Ufpr) Considere um edifício em construção,
constituído pelo andar térreo e mais dez
andares. Um servente de pedreiro deixou cair
um martelo cuja massa é 0,5 kg a partir de
uma altura do piso do décimo andar. Suponha
que cada andar tem uma altura de 2,5 m e que
o martelo caiu verticalmente em queda livre
partindo do repouso. Considere a aceleração da
gravidade igual a 10 m/s2 e o martelo como
uma partícula. Despreze a resistência do ar, a
ação do vento e a espessura de cada piso.
Levando em conta as informações dadas,
analise as seguintes afirmativas:
Os esquiadores partem do repouso no ponto A
e percorrem a pista sem receber nenhum
empurrão, nem usam os bastões para alterar
2
sua velocidade. Adote g  10 m / s e
despreze o atrito e a resistência do ar.
a) Se um esquiador passar pelo ponto
pista com velocidade
10 2 m s,
B da
com que
velocidade ele passará pelo ponto
C?
b) Qual a maior altura hA do ponto A,
indicada na figura, para que um esquiador
não perca contato com a pista em nenhum
ponto de seu percurso?
5. (G1 - ifsc) A figura desta questão mostra
uma bola de gude, de massa m, presa por uma
barra rígida de massa desprezível, de
comprimento , a uma haste engastada na
parede.
1. A velocidade do martelo ao passar pelo teto
do 1° andar era 20 m/s.
2. A energia cinética do martelo ao passar pelo
piso do 5° andar era maior que 100 J.
3. Se a massa do martelo fosse o dobro, o
tempo de queda até o chão diminuiria pela
metade.
Assinale a alternativa correta.
a) Somente a afirmativa 1 é verdadeira.
b) Somente a afirmativa 2 é verdadeira.
c) Somente as afirmativas 1 e 2 são
verdadeiras.
d) Somente as afirmativas 2 e 3 são
verdadeiras.
e) As afirmativas 1, 2 e 3 são verdadeiras.
7. (Uece) Uma pessoa, do alto de um prédio de
altura H, joga uma bola verticalmente para
baixo, com uma certa velocidade de
lançamento. A bola atinge o solo com
velocidade cujo módulo é VI. Em um segundo
experimento, essa mesma bola é jogada do
mesmo ponto no alto do prédio, verticalmente
para cima e com mesmo módulo da velocidade
de lançamento que no primeiro caso. A bola
sobe até uma altura H acima do ponto de
lançamento e chega ao solo com velocidade
cujo módulo é VII. Desprezando todos os atritos
e considerando as trajetórias retilíneas, é
correto afirmar-se que
a) VI  2VII.
VI  VII.
c) VI  VII / 2.
d) VI  VII / 4.
b)
Considerando a aceleração da gravidade
constante e igual g, e desprezando a
resistência do ar, é CORRETO afirmar que a
menor velocidade v 0 para que a bola de gude
8. (Espcex (Aman)) Uma esfera é lançada com
velocidade horizontal constante de módulo v=5
m/s da borda de uma mesa horizontal. Ela
atinge o solo num ponto situado a 5 m do pé da
mesa conforme o desenho abaixo.
consiga chegar ao topo é:
a)
v0  g
b)
v0  5g
c)
v0  2 g
d)
v0  g m
Página 13 de 31
a) a velocidade do volume de água ΔV ao
chegar à turbina na base da barragem;
b) a potência útil da usina, se sua eficiência em
todo o processo de produção de energia
elétrica for de 30%, para uma vazão de água
6
3
de 120  10 cm / s
11. (Uerj) Duas gotas de orvalho caem de uma
mesma folha de árvore, estando ambas a uma
altura h do solo. As gotas possuem massas m1
e
Desprezando a resistência do ar, o módulo da
velocidade com que a esfera atinge o solo é de:
Dado: Aceleração da gravidade: g=10 m/s
a) 4 m / s
b)
5m/s
c)
5 2 m/ s
d)
6 2 m/ s
e)
5 5 m/ s
2
m2 , sendo m2  2m1. Ao atingirem o solo,
suas velocidades e energias cinéticas são,
respectivamente, v1, E1 e v 2 , E2 .
Desprezando o atrito e o empuxo, determine as
razões
v1
E
e 1.
v2
E2
12. (Upe) Duas partículas de massas M e 2M
foram fixadas em uma estrutura com formato
de roda, de raio R e massa desprezível. A
configuração inicial desse sistema está
ilustrada na figura a seguir:
9. (Unifor) A figura a seguir mostra uma das
cenas vistas durante a Copa das Confederações
no Brasil. Os policiais militares responderam às
ações dos manifestantes com bombas de gás
lacrimogêneo e balas de borracha em uma
região totalmente plana onde era possível
avistar a todos.
Suponha que o projétil disparado pela arma do
PM tenha uma velocidade inicial de
200,00 m / s ao sair da arma e sob um ângulo
de 30,00º com a horizontal. Calcule a altura
máxima do projétil em relação ao solo,
sabendo-se que ao deixar o cano da arma o
projétil estava a 1,70 m do solo.
Despreze as forças dissipativas e adote
2
g  10,00 m / s .
a) 401,70 m
b) 501,70 m
c) 601,70 m
d) 701,70 m
e) 801,70 m
10. (Ufg) Para fazer um projeto da barragem
de uma usina hidrelétrica de 19,8 m de altura,
o projetista considerou um pequeno volume de
água ΔV caindo do topo da barragem a uma
velocidade inicial de 2 m/s sobre as turbinas na
base da barragem. Considerando o exposto,
calcule:
Dados:
Densidade da água:
g = 10m/s2
ρ  1 g / cm3
Sabendo-se que o conjunto é abandonado do
repouso, obtenha uma expressão para a
velocidade da partícula 2M, quando a partícula
de massa M passar pela posição o mais alto
possível pela primeira vez.
1/2
a) v  2gR / 3


b)
v  2gR / 3
c)
v 2  gR
d)
v   2gR 
e)
v  2gR
1/2
Eletrodinâmica Lâmpadas
1. Uma vez que a produção de energia
elétrica, em qualquer de suas modalidades, tem
impactos ambientais, inovações que levem à
diminuição do consumo de energia são
necessárias. Assim, as antigas lâmpadas
incandescentes vêm sendo substituídas por
alternativas energeticamente mais eficientes.
Naquele tipo de lâmpada, a emissão de luz
ocorre quando a temperatura de um filamento
de tungstênio é elevada a valores entre 2.700
e
3.300K. Esse aquecimento ocorre como
Página 14 de 31
resultado da dissipação da energia dos elétrons
ao serem transportados através do condutor.
Aquecimento e emissão de radiação
infravermelha consomem cerca de 90% da
energia elétrica fornecida para a lâmpada. Com
base nesse conhecimento, considere a situação
representada na tira a seguir.
mesmo material, mesmo comprimento, mas é
mais grosso que o filamento da lâmpada 1.
Por que uma lâmpada incandescente de
100 W a 110 V, como a usada pelo
Nessas condições, a alternativa correta é:
a) Desligando a lâmpada L1, a lâmpada L2
diminui o seu brilho.
b) A lâmpada L1 brilha mais que a lâmpada L2.
c) As lâmpadas L1 e L2 tem o mesmo brilho.
d) A lâmpada L2 brilha mais que a lâmpada L1.
personagem da tira, queima quando ligada em
uma rede de 220 V ?
4.
a) Ao dobrar a tensão, a lâmpada dissipa
energia a uma taxa quatro vezes maior.
b) Ao dobrar a tensão, a lâmpada dissipa
energia a uma taxa duas vezes maior.
c) Ao dobrar a corrente, a lâmpada dissipa
energia a uma taxa duas vezes maior.
d) Ao dobrar a corrente, a resistência da
lâmpada cai à metade.
e) Ao dobrar a corrente, a potência da lâmpada
cai à metade.
2. Para responder à questão, considere o
texto e a figura abaixo.
No circuito abaixo, estão representadas três
lâmpadas idênticas, L1 L 2 e L3 , associadas
por fios condutores ideais a uma bateria ideal
B. Cada uma das lâmpadas dissipa,
respectivamente, uma potência P1, P2 e P3 .
Duas lâmpadas,
L1 e L2 , estão conectadas
em paralelo a uma bateria de automóvel. A
corrente em
L1 é igual a
1
da corrente em
3
L2 .
Admita que
P1 e P2 sejam as potências
dissipadas, respectivamente, por L1 e L2 .
A razão
P1
corresponde a:
P2
1
9
1
b)
3
a)
c) 1
d) 3
5. Têm-se duas lâmpadas com os seguintes
dados nominais: L1 (40 W e 220 V) e L 2
(60 W e 220 V).
Sobre elas, afirma-se que:
I. Ao ligá-las em série, na rede de
lâmpada
220 V, a
L1 brilha mais intensamente;
Sobre a potência elétrica dissipada pelas
lâmpadas, é correto afirmar que:
a) P1  P2  P3
P1  P2  P3
P1  P2  P3
d) P1  P2  P3
e) P1  P2  P3
b)
c)
II. Ao ligá-las em paralelo, na rede de
a lâmpada
220 V,
L 2 brilha mais intensamente;
3. Em uma situação cotidiana, uma pessoa
liga duas lâmpadas incandescentes em paralelo
em uma rede de 220V. As lâmpadas
apresentam certa intensidade luminosa (brilho),
sendo que a lâmpada 2 tem um filamento de
Página 15 de 31
III. Ao ligar a lâmpada
L 2 na rede de 110 V,
seu brilho é menor que quando ligada em
220 V.
Considerando essa associação entre as
lâmpadas, é correto afirmar que
a) a intensidade da corrente elétrica é diferente
nas lâmpadas 1 e 2.
b) a diferença de potencial é diferente nas
lâmpadas 1 e 2.
c) a intensidade de corrente elétrica na
lâmpada 2 é maior do que na 3.
d) cada uma das lâmpadas 1 e 2 está sujeita à
diferença de potencial de 6,0 V.
e) cada uma das lâmpadas 3 e 4 está sujeita à
diferença de potencial de 12 V.
8. O circuito elétrico seguinte é constituído por
três lâmpadas L1 , L2 e L3, que são idênticas, e
ligadas a uma bateria ε.
Dessas afirmativas:
a) apenas I está correta.
b) apenas II está correta.
c) apenas I e II estão corretas.
d) apenas I e III estão corretas.
e) I, II e III estão corretas.
6. As três lâmpadas, L1, L2 e L3, ilustradas na
figura a seguir, são idênticas e apresentam as
seguintes informações nominais: 0,5 W — 6,0
V. Se a diferença de potencial elétrico entre os
terminais A e B for 12 V, para que essas
lâmpadas possam ser associadas de acordo
com a figura e “operando” segundo suas
especificações de fábrica, pode-se associar a
elas o resistor de resistência elétrica R igual a
a) 6 Ù
b) 12 Ù
c) 18 Ù
d) 24 Ù
e) 30 Ù
7. O circuito alimentado com uma diferença de
potencial de 12 V, representado na figura a
seguir, mostra quatro lâmpadas associadas,
cada uma com a inscrição 12 V / 15 W.
Se a lâmpada L3 repentinamente se queimar, é
correto afirmar que
a) L2 diminuirá o seu brilho.
b) L1 dissipará mais energia.
c) L2 dissipará menos energia.
d) L1 terá o mesmo brilho de L2.
9. Considere o circuito formado por três
lâmpadas idênticas ligadas em paralelo à
bateria, conforme representa a figura (1).
Como a chave C foi aberta na figura (2),
considere as afirmações abaixo sobre a figura
(2), em comparação à situação descrita na
figura (1).
I. A potência fornecida pela bateria é a mesma.
Página 16 de 31
II. A diferença de potencial aplicada a cada
lâmpada acesa é a mesma.
III. As correntes elétricas que percorrem as
lâmpadas acesas são menores.
Quais estão corretas?
a) Apenas II.
b) Apenas III.
c) Apenas I e II.
d) Apenas I e III.
e) I, II e III.
10. Em uma experiência, três lâmpadas
idênticas {L1, L2, L3} foram inicialmente
associadas em série e conectadas a uma
bateria E de resistência interna nula. Cada uma
dessas lâmpadas pode ser individualmente
ligada à bateria E sem se queimar.
Observe o esquema desse circuito, quando as
três lâmpadas encontram-se acesas:
II. a grandeza que é chamada de pressão é a
energia que as moléculas do gás transferem
às paredes do recipiente que contém esse
gás.
III. a energia interna do gás é igual à soma das
energias cinéticas das moléculas desse gás.
Está(ão) correta(s)
a) apenas I.
b) apenas II.
c) apenas III.
d) apenas I e III.
e) I, II e III.
2. Na figura seguinte, é indicado um sistema
termodinâmico com processo cíclico. O ciclo é
constituído por duas curvas fechadas, a malha I
e a malha II.
Em seguida, os extremos não comuns de L1 e L2
foram conectados por um fio metálico,
conforme ilustrado abaixo:
A afirmativa que descreve o estado de
funcionamento das lâmpadas nessa nova
condição é:
a) As três lâmpadas se apagam.
b) As três lâmpadas permanecem acesas.
c) L1 e L2 se apagam e L3 permanece acesa.
d) L3 se apaga e L1 e L2 permanecem acesas.
Energia interna
É correto afirmar:
a) Durante um ciclo completo, o sistema não
realiza trabalho.
b) O sistema realiza trabalho positivo na malha
I.
c) O sistema libera calor na malha II.
d) Durante um ciclo completo, a variação da
energia interna é nula.
1. A respeito dos gases que se encontram em
condições nas quais seu comportamento pode
ser considerado ideal, afirma-se que
I. a grandeza que é chamada de temperatura é
proporcional à energia cinética média das
moléculas.
3. Ao realizar um trabalho de 80 mil calorias,
um sistema termodinâmico recebeu 60 mil
calorias.
Pode-se afirmar que, nesse processo, a energia
interna desse sistema
Página 17 de 31
a) aumentou 20 mil calorias.
b) diminuiu 20 mil calorias.
c) aumentou 60 mil calorias.
d) diminuiu 80 mil calorias.
e) se conservou.
4. O diagrama PV mostrado a seguir ilustra
dois processos termodinâmicos: 1 ABC e 2
ADC, em que um gás ideal é levado de um
estado A para outro C. considerando V2 = 2V1 e
P2 = 4P1, é CORRETO afirmar:
Em relação a essa transformação, é
INCORRETO afirmar:
a) O trabalho realizado pelo gás no ciclo U
E

G

O

I

A

S


Ué
igual à quantidade de calor recebida.
b) A variação da energia interna do gás no ciclo
U  E  G  O  I  A  S 
U é não nula.
c) O trabalho realizado pelo gás, no trecho S
 U, é negativo.
d) A quantidade de calor recebida pelo gás no
ciclo U  E  G  O  I  A  S

U é o valor negativo da área hachurada
na figura.
a) O trabalho realizado pelo gás ao longo do
processo ADC é maior do que o trabalho
realizado ao longo do processo ABC.
b) A energia interna do gás é maior no estado
B.
c) O trabalho realizado pelo gás ao longo do
processo ABC é 4 P1V1.
d) A razão TA/TB, em que TA e TB representam
as temperaturas do gás nos estados A e B, é
1/8.
5. Pode-se afirmar corretamente que a energia
interna de um sistema constituído por um gás
ideal
a) diminui em uma expansão isotérmica.
b) aumenta em uma expansão adiabática.
c) diminui em uma expansão livre.
d) aumenta em uma expansão isobárica.
7. Cotidianamente são usados recipientes de
barro (potes, quartinhas, filtros etc.) para
esfriar um pouco a água neles contida.
Considere um sistema constituído por uma
quartinha cheia d'água. Parte da água que
chega à superfície externa da quartinha,
através de seus poros, evapora, retirando calor
do barro e da água que o permeia. Isso implica
que também a temperatura da água que está
em seu interior diminui nesse processo.
Tal processo se explica porque, na água que
evapora, são as moléculas de água
a) com menor energia cinética média que
escapam do líquido, aumentando, assim, a
energia cinética média desse sistema.
b) que, ao escaparem do líquido, aumentam a
pressão atmosférica, diminuindo, assim, a
pressão no interior da quartinha.
c) com maior energia cinética média que
escapam do líquido, diminuindo, assim, a
energia cinética média desse sistema.
d) que, ao escaparem do líquido, diminuem a
pressão atmosférica, aumentando, assim, a
pressão no interior da quartinha.
6. O gráfico a seguir representa um processo
termodinâmico hipotético, no qual certa massa
de gás sofre a transformação cíclica, U  E
 G  O  I  A  S  U,
Página 18 de 31
Máquinas
térmicas
1. Um técnico de manutenção de máquinas pôs
para funcionar um motor térmico que executa
20 ciclos por segundo. Considerando-se que,
em cada ciclo, o motor retira uma quantidade
de calor de 1200 J de uma fonte quente e cede
800 J a uma fonte fria, é correto afirmar que o
rendimento de cada ciclo é
reversível, o ciclo termodinâmico realizado
pela substância de trabalho é formado por
duas isotermas e duas adiabáticas.
III. Como o reservatório de temperatura mais
alta perde energia e o reservatório de
temperatura mais baixa ganha energia, T2
diminui e T1 aumenta; por isso o rendimento
diminui com o tempo.
Está(ão) correta(s)
a) apenas I.
a) 13,3%
b) apenas II.
b) 23,3%
c) apenas III.
c) 33,3%
d) apenas I e II.
d) 43,3%
e) apenas II e III.
e) 53,3%
3. Assinale o que for correto.
2. Na primeira fase da revolução industrial, o
processo de exploração do carvão, na
Inglaterra, foi melhorado com a utilização de
máquinas a vapor, para retirar a água
acumulada nas minas. Considere uma máquina
a vapor representada pelo esquema seguinte:
01) Condução térmica e radiação térmica são
os únicos processos de transferência de
calor.
02) 1 caloria é a quantidade de calor necessária
para elevar a temperatura de 1 g de água
em
1º C , no intervalo de 14,5º C a
15,5º C a 1 atm.
04) Nenhuma máquina térmica, operando em
ciclos, pode retirar calor de uma fonte e
transformá-lo integralmente em trabalho.
08) O ciclo de Carnot descreve o rendimento
máximo de uma máquina térmica.
16) O princípio de funcionamento de um
refrigerador é baseado nos processos de
compressão e expansão de um gás.
Q2 é a energia retirada do reservatório de maior
temperatura (T2) a cada ciclo. Q1 é a energia
cedida ao reservatório de menor temperatura
(T1). W é a energia associada ao trabalho da
máquina sobre a vizinhança. Então, analise as
afirmativas:
I. Pela primeira lei da Termodinâmica, em
valores absolutos, Q1+Q2 = W.
II. Se o esquema representa uma máquina
TEXTO PARA A PRÓXIMA QUESTÃO:
Equipe de cientistas descobre o primeiro
exoplaneta habitável
O primeiro exoplaneta habitável foi
encontrado depois de observações que duraram
11 anos, utilizando uma mistura de técnicas
avançadas e telescópios convencionais. A
equipe descobriu mais dois exoplanetas
orbitando em volta da estrela Gliese 581.
O mais interessante dos dois
exoplanetas descobertos é o Gliese 581g, com
uma massa três vezes superior à da Terra e um
período orbital (tempo que o planeta leva para
Página 19 de 31
dar uma volta completa em torno de sua
estrela) inferior a 37 dias. O raio da órbita do
Gliese 581g é igual à 20% do raio da órbita da
Terra, enquanto sua velocidade orbital é 50%
maior que a velocidade orbital da Terra. O
Gliese 581g está "preso" à estrela, o que
significa que um lado do planeta recebe luz
constantemente, enquanto o outro é de
perpétua escuridão. A zona mais habitável na
superfície do exoplaneta seria a linha entre a
sombra e a luz, com temperaturas caindo em
direção à sombra e subindo em direção à luz. A
temperatura média varia entre -31ºC e -12ºC,
mas as temperaturas reais podem ser muito
maiores na região de frente para a estrela (até
70 ºC) e muito menores na região contrária
(até -40ºC). A gravidade no Gleise 581g é
semelhante à da Terra, o que significa que um
ser humano conseguiria andar sem dificuldades.
Os cientistas acreditam que o número
de exoplanetas potencialmente habitáveis na
Via Láctea pode chegar a 20%, dada a
facilidade com que Gliese 581g foi descoberto.
Se fossem raros, dizem os astrônomos, eles
não teriam encontrado um tão rápido e tão
próximo. No entanto, ainda vai demorar muito
até que o homem consiga sair da Terra e
comece a colonizar outros planetas fora do
sistema solar.
Texto adaptado de artigo da Revista VEJA,
Edição 2185, ano 43, n 40 de 06 de outubro de
2010.
d) III e IV são verdadeiras.
e) II e IV são verdadeiras.
TEXTO PARA A PRÓXIMA QUESTÃO:
Nesta prova, quando necessário, adote os
seguintes valores:
Aceleração da gravidade: g = 10 m/s2 .
Constante da gravitação universal: G = 6 x
10−11 N m2 / kg2 .
Velocidade do som no ar: v = 340 m/s .
Massa da Terra: M = 6 x 1024 kg.
Constante π = 3.
5. Uma máquina térmica opera usando um gás
ideal monoatômico, de acordo com o ciclo
representado na figura abaixo.
4. Suponha que uma máquina de Carnot seja
construída utilizando como fonte fria o lado do
planeta Gliese 581g que nunca recebe luz e
como fonte quente o lado que sempre recebe
luz. A temperatura da fonte fria Tf = -40ºC e da
fonte quente Tq = 70ºC. A cada ciclo a máquina
retira da fonte quente 1000J de calor.
Considerando que a máquina trabalha com um
gás ideal, leia os itens abaixo:
I. A máquina pode ser representada por um
ciclo com duas transformações adiabáticas
reversíveis e duas transformações
isotérmicas reversíveis.
II. Se o ciclo desta máquina consiste de uma
expansão isotérmica, uma expansão
adiabática, uma compressão isotérmica e
uma compressão adiabática,
respectivamente, então ocorre
transformação de calor em trabalho útil.
III. O rendimento da máquina é maior do que
40%.
IV. A cada ciclo uma quantidade de calor maior
que 700J é rejeitada para a fonte fria.
Marque a opção correta:
a) I e III são verdadeiras.
b) I e II são verdadeiras.
c) I e IV são verdadeiras.
Sabendo que a temperatura de operação da
máquina no ponto B é de 500 K, identifique as
afirmativas corretas:
(
) O trabalho realizado pela máquina
térmica em um ciclo é de 4 x 105 J.
(
) A eficiência dessa máquina é igual à
eficiência de uma máquina operando
segundo o ciclo de Carnot.
(
) A menor temperatura atingida durante o
ciclo de operação da máquina é de 100 K.
(
) Para uma máquina térmica ideal que
trabalhe entre as temperaturas de
operação do ciclo representado na figura,
a maior eficiência possível é de 0,7.
Página 20 de 31
(
) A variação de energia interna em um
ciclo completo é nula.
6. No diagrama p x V a seguir, está
representado o ciclo termodinâmico da máquina
de Carnot, considerada ideal porque tem o
maior rendimento entre as máquinas térmicas.
O sistema recebe calor da fonte quente à
temperatura T1 e transfere calor para a fonte
fria à temperatura T2.
04) A 2a lei da termodinâmica afirma que é
indiferente transformar integralmente calor
em trabalho ou trabalho em calor.
08) Parcela da energia envolvida em um
processo irreversível torna-se indisponível
para a realização de trabalho.
16) Em um processo cíclico a energia interna do
sistema apresenta variação nula.
8. Para responder a questão, considere o
texto e o gráfico, o qual relaciona o rendimento
de uma máquina de Carnot e a razão T2/T1 das
temperaturas em que opera a máquina.
O ciclo de Carnot é um ciclo termodinâmico
especial, pois uma máquina térmica que opera
de acordo com este ciclo entre duas
temperaturas T1 e T2, com T1 maior do que T2,
obtém o máximo rendimento possível. O
rendimento r de uma máquina térmica é
definido como a razão entre o trabalho líquido
que o fluido da máquina executa e o calor que
absorve do reservatório à temperatura T1.
Com relação às transformações termodinâmicas
que constituem esse ciclo, é correto afirmar que
o sistema passa por uma:
a) expansão adiabática entre os estados b e d
(b → d).
b) expansão isovolumética entre os estados b e
c (b → c).
c) compressão isobárica entre os estados c e d
(c → d).
d) expansão isotérmica entre os estados a e b
(a → b).
e) compressão isotérmica entre os estados d e
a (d → a).
Pode-se concluir, pelo gráfico e pelas leis da
termodinâmica, que o rendimento da máquina
de Carnot aumenta quando a razão T2/T1
diminui,
a) alcançando 100% quando T2 vale 0ºC.
b) alcançando 100% quando T1 é muito maior
do que T2.
7. A termodinâmica pode ser definida como
uma ciência experimental baseada em um
pequeno número de princípios (leis da
termodinâmica), que são generalizações feitas
a partir da experiência. Sobre as leis da
termodinâmica, assinale o que for correto.
01) Nenhuma máquina térmica pode apresentar
um rendimento superior ao de uma
máquina de Carnot operando entre as
mesmas temperaturas.
02) A 1a lei da termodinâmica é uma afirmação
do princípio geral da conservação da
energia.
c) alcançando 100% quando a diferença entre
T1 e T2 é muito pequena.
d) mas só alcança 100% porque representa o
ciclo ideal.
e) mas nunca alcança 100%.
9. Um processo cíclico de Carnot possui um
rendimento de 50%.
Uma máquina real, que opera sob as mesmas
condições térmicas desse ciclo, apresentará um
rendimento térmico r, tal que
Página 21 de 31
a) r

50%.
b) r = 50%.
c) r > 50%.
d) r < 50%.
10. A cada ciclo de funcionamento, o motor de
um certo automóvel retira 40 kJ do
compartimento da fonte quente, onde se dá a
queima do combustível, e realiza 10 kJ de
trabalho. Sabendo que parte do calor retirado
da fonte quente é dispensado para o ambiente
(fonte fria) a uma temperatura de 27 ºC, qual
seria a temperatura no compartimento da fonte
quente se esse motor operasse segundo o ciclo
de Carnot?
12. Um aluno, estudando física térmica, fez as
seguintes afirmações:
(
Dado: considere que as temperaturas em graus
centígrados, TC, e Kelvin, TK, se relacionam
através da expressão TC = TK − 273.
a) 127 ºC
b) 177 ºC
c) 227 ºC
d) 277 ºC
) A variação da energia interna de um
sistema em um processo termodinâmico
é a diferença entre o trabalho realizado
e o calor trocado com o meio.
(
) O rendimento máximo de uma máquina
térmica é 1.
(
) A energia do universo sempre se mantém
constante.
(
) O calor sempre flui espontaneamente de
um corpo quente para um corpo frio.
e) 377 ºC
11. Leia o texto a seguir.
"Por trás de toda cerveja gelada, há sempre um
bom freezer. E por trás de todo bom freezer, há
sempre um bom compressor - a peça mais
importante para que qualquer sistema de
refrigeração funcione bem. Popularmente
conhecido como 'motor', o compressor
hermético é considerado a alma de um sistema
de refrigeração. A fabricação desses aparelhos
requer tecnologia de ponta, e o Brasil é
destaque mundial nesse segmento".
Classifique as afirmações anteriores como
verdadeiras (V) ou falsas (F), baseando-se,
somente, no enunciado da Segunda Lei da
Termodinâmica, e assinale a opção que contém
a sequência correta, de cima para baixo.
a) V, F, V, F
b) V, F, V, V
c) F, V, V, F
d) F, F, F, V
(KUGLER, H. Eficiência gelada. "Ciência
Hoje". v. 42, n. 252. set. 2008. p. 46.)
Assinale a alternativa que representa
corretamente o diagrama de fluxo do
refrigerador.
13. Uma máquina térmica percorre o ciclo
descrito pelo gráfico a seguir. A máquina
absorve 6,0 x 105 J de energia térmica por
ciclo.
Página 22 de 31
refrigerante.
III - O gás refrigerante é uma substância com
baixo calor latente de vaporização.
IV - O processo de refrigeração realiza trabalho
ao retirar calor da fonte fria e transferi-lo para
a fonte quente.
Assinale a alternativa CORRETA.
a) Somente as afirmativas I e II são corretas.
b) Somente as afirmativas I e III são corretas.
Responda ao que se pede.
a) Qual é a variação na energia interna no ciclo
ABCA? Justifique.
b) Calcule o trabalho realizado pelo motor em
um ciclo.
c) Calcule a quantidade de energia térmica
transmitida à fonte fria.
d) Calcule o rendimento dessa máquina
térmica.
14. Um automóvel com motor 1.0 (volume de
1,0 litro), conhecido pelo seu menor consumo
de combustível, opera com pressão média de 8
atm e 3300 rpm (rotações por minuto), quando
movido a gasolina. O rendimento desse motor,
que consome, nestas condições, 4,0 g/s
(gramas por segundo) de combustível, é de
aproximadamente
c) Somente as afirmativas III e IV são corretas.
d) Somente as afirmativas I, II e IV são
corretas.
e) Somente as afirmativas II, III e IV são
corretas.
Calorimetria
1. Analise o gráfico a seguir, que indica a
variação da capacidade térmica de um corpo
(C) em função da temperatura (θ).
Considere:
- Calor de combustão da gasolina = 11.100
cal/g
- 1atm = 105 N/m2
- 1cal = 4 J
- 1L = 10-3 m3
- 1 rotação corresponde a 1 ciclo
a) 18%
A quantidade de calor absorvida pelo material
até a temperatura de 50 C, em calorias, é
b) 21%
igual a:
a) 500
c) 25%
b)
d) 27%
e) 30%
15. A conservação de alimentos pelo frio é
uma das técnicas mais utilizadas no dia a dia,
podendo ocorrer pelos processos de
refrigeração ou de congelamento, conforme o
tipo de alimento e o tempo de conservação
desejado.
1500
c) 2000
d) 2200
2. É muito comum o amplo uso de aparelhos
de ar-condicionado durante o verão intenso do
Recife. Nessa cidade, uma residência possui
2
uma parede de área 40 m e espessura
20 cm, separando o ambiente interior do
exterior. Se a temperatura externa é de 33 C
e deseja-se manter a interna igual a 23 C,
Sobre os refrigeradores, considere as
afirmativas.
qual será o gasto por hora de aparelho ligado,
considerando-se, apenas, essa parede
separadora?
I - O refrigerador é uma máquina que transfere
calor.
Dados: A condutividade térmica da parede é
3
igual a 1,25  10
kW (mK), e o custo da
II - O funcionamento do refrigerador envolve os
ciclos de evaporação e de condensação do gás
energia elétrica em
kWh é de R$ 0,60.
Página 23 de 31
a)
b)
c)
d)
e)
3.
e)
R$ 0,30.
R$ 0,90.
R$ 1,20.
R$ 1,50.
R$ 2,50.
Uma forma de gelo com água a
25 C é
colocada num freezer de uma geladeira para
formar gelo. O freezer está no nível de
congelamento mínimo, cuja temperatura
corresponde a 18 C.
As etapas do processo de trocas de calor e de
mudança de estado da substância água podem
ser identificadas num gráfico da temperatura X
quantidade de calor cedida.
Qual dos gráficos a seguir mostra,
corretamente (sem considerar a escala), as
etapas de mudança de fase da água e de seu
resfriamento para uma atmosfera?
a)
4. No preparo de uma xícara de café com
leite, são utilizados 150 mL (150g) de café, a
80 C, e 50 mL (50g) de leite, a 20  C.
Qual será a temperatura do café com leite?
(Utilize o calor específico do café = calor
específico do leite  1,0 cal/ g  C)
a)
b)
c)
d)
e)
65 C
50 C
75 C
80 C
90 C
5. Em um experimento que recebeu seu
nome, James Joule determinou o equivalente
mecânico do calor: 1cal  4,2 J. Para isso, ele
b)
utilizou um dispositivo em que um conjunto de
paletas giram imersas em água no interior de
um recipiente.
Considere um dispositivo igual a esse, no qual a
energia cinética das paletas em movimento,
totalmente convertida em calor, provoque uma
variação de 2 C em 100 g de água. Essa
quantidade de calor corresponde à variação da
energia cinética de um corpo de massa igual a
10 kg ao cair em queda livre de uma
c)
determinada altura.
Essa altura, em metros, corresponde a:
a) 2,1
b)
c)
d)
4,2
8,4
16,8
6. A perspectiva de uma pessoa que usa uma
garrafa térmica é que esta não permita a troca
de calor entre o meio ambiente e o conteúdo da
garrafa. Porém, em geral, a própria garrafa já
provoca uma pequena redução de temperatura
quando nela colocamos um líquido quente,
como o café, uma vez que a capacidade térmica
da garrafa não é nula.
Numa garrafa térmica que está a 24 C
colocam-se
500 g de água (c  1cal g C) a
90 C e, após algum tempo, nota- se que a
d)
temperatura estabiliza em
84 C. Pode-se
afirmar que a capacidade térmica desta garrafa
é, em cal C,
a)
b)
5.
6.
Página 24 de 31
c)
50.
60.
e) 100.
9. Uma chapa de alumínio retangular tem
massa de 200 g e uma temperatura inicial de
d)
15 C. Sendo o coeficiente de dilatação linear
7. Analise cada uma das afirmativas abaixo,
indicando, nos parênteses, se é verdadeira ou
falsa, de acordo com o estudo da Calorimetria.
(
) A temperatura de
104 F corresponde a
40 C.
(
(
(
(
) A dilatação real de um líquido, quando
aquecido, representa a dilatação do
frasco mais a dilatação aparente do
líquido.
) A transmissão de calor por convecção
promove o movimento das camadas de
um líquido ou de ar, sendo que as
camadas frias sobem e as camadas
quentes descem, devido à diferença de
densidade entre elas.
) A mudança de fase ocorre sempre
que,sob pressão constante, uma
substância pura receba ou ceda calor,
sem que ocorra variação de temperatura.
) A dilatação de uma certa massa de gás
perfeito, que sofre uma transformação
isobárica, faz com que um aumento de
temperatura sobre esse gás provoque um
aumento em seu volume.
22  106 C1, calor
específico do alumínio igual a 0,217 cal g C,
largura da chapa 50 cm e altura de 20 cm; se
do alumínio igual a
essa barra for aquecida até a temperatura de
60 C, a sua superfície final e a quantidade de
calor necessário para que esse aumento ocorra
serão, respectivamente,
2
a) 1.001,980 cm e 19.500 cal
b)
1.002,640 cm2 e 2.640 cal
c)
1.001,980 cm2 e 1.950 cal
d)
1.002,640 cm2 e 26.400 cal
10. Analise as afirmações a seguir e assinale
(V) para as verdadeiras ou (F) para as falsas.
(
(
A sequência correta, de cima para baixo, é
a) V - V - F - F - V.
b) V - V - F - V - V.
c) V - F - F - V - V.
d) V - F - V - F - V.
(
8. Um estudante de física, durante seu
intervalo de aula, preparou um café. Durante o
processo, ele utilizou uma vasilha com 1 litro
de água cuja temperatura inicial era de
21,0 C. Ele lembrou ter ouvido, em suas aulas
(
de Laboratório de Física II, que a água em Juiz
de Fora entra em ebulição a 98,3 C. Sabendo
que os processos ocorreram à pressão
constante, o estudante chega às seguintes
conclusões:
I. Levando-se em conta que o calor especifico
da água é aproximadamente 1,0 cal g C, a
energia gasta para aquecer a água até a
ebulição foi de 77.300,0 cal;
II. Após a água entrar em ebulição, a
temperatura da água aumentou até
118,3 C;
III. Durante o processo de aquecimento, o
volume de água não se alterou;
IV. A quantidade de calor fornecida para água,
após ela entrar em ebulição, é gasta na
transformação de fase líquido/gás.
Marque a alternativa CORRETA.
a) I e IV estão corretas.
b) IV e II estão incorretas.
c) II e III estão corretas.
d) III e IV estão corretas.
e) Todas as afirmativas estão corretas.
) Ao segurar um corrimão de madeira e
outro de metal, ambos à mesma
temperatura, tem-se a sensação de que a
madeira está mais quente porque ela
conduz melhor o calor.
) Uma geladeira funcionando dentro de
uma cozinha, sempre causará o
aquecimento do ambiente.
) Considere dois materiais diferentes, de
mesma massa e à mesma temperatura.
Para que eles sejam aquecidos até
atingirem uma mesma temperatura final,
a quantidade de calor necessária será a
mesma.
) Considere dois materiais iguais, de
volumes diferentes e à mesma
temperatura. Para que eles sejam
aquecidos até atingirem uma mesma
temperatura final, a quantidade de calor
necessária será a mesma.
A sequência correta encontrada é
a) F, F, V, V.
b) V, V, F, F.
c) F, V, F, F.
d) V, F, F, V.
Dilatação
1.
Por que os lagos congelam só na superfície?
Porque a camada de gelo funciona como uma
espécie de cobertor, impedindo que a água
mais profunda congele. "A capa gelada faz o
papel de isolante térmico. Como o gelo é um
mau condutor, ele evita que o resto da água
perca calor para a atmosfera", afirma o
glaciologista Jefferson Cardia Simões, da
Universidade Federal do Rio Grande do Sul
(UFRGS).
Disponível em:
Página 25 de 31
http://mundoestranho.abril.com.br/materia/por
-que-os-lagos-congelam-so-na-superficie,
acessado em:
O comportamento diferenciado da densidade da
água em baixas temperaturas, quando
comparada com outras substâncias, permite
que o fundo dos lagos não congele,
preservando a vida nesses ecossistemas, nos
períodos de inverno. Sobre isso, o gráfico que
melhor descreve a variação da densidade da
água, d, com a temperatura, T, está indicado
na alternativa
a)
doméstico que consiste em um líquido como o
mercúrio colocado dentro de um tubo de vidro
graduado, fechado em uma das extremidades e
com uma escala indicando os valores de
temperatura. Em seguida, coloca-se o
termômetro debaixo da axila e aguardam-se
alguns minutos para fazer a leitura.
As afirmativas a seguir referem-se ao
funcionamento do termômetro.
I. A temperatura marcada no termômetro
coincidirá com a temperatura de ebulição do
mercúrio do dispositivo.
II. A temperatura marcada na escala do
termômetro está relacionada com a dilatação
térmica do mercúrio.
III. O tempo de espera citado acima refere-se
ao tempo necessário para que se atinja o
equilíbrio térmico entre o paciente e o
termômetro.
IV. Se a substância do mesmo termômetro for
trocada por álcool, a temperatura indicada
será a mesma.
As afirmativas corretas são
a) I e II.
b) I e IV.
c) II e III.
d) III e IV.
b)
4. Dois copos de vidro iguais, em equilíbrio
térmico com a temperatura ambiente, foram
guardados, um dentro do outro, conforme
mostra a figura. Uma pessoa, ao tentar
desencaixá-los, não obteve sucesso. Para
separá-los, resolveu colocar em prática seus
conhecimentos da física térmica.
c)
d)
e)
2. Com base nos conhecimentos acerca da
expansão térmica dos sólidos, sabe-se que, ao
aquecer uma esfera feita de alumínio, em
100C, o maior aumento percentual vai
ocorrer na (no)
a) sua área de superfície.
b) seu volume.
c) seu diâmetro.
d) sua densidade.
e) sua massa.
3. Para verificar se uma pessoa está febril,
pode-se usar um termômetro clínico de uso
De acordo com a física térmica, o único
procedimento capaz de separá-los é:
a) mergulhar o copo B em água em equilíbrio
térmico com cubos de gelo e encher o copo
A com água à temperatura ambiente.
b) colocar água quente (superior à temperatura
ambiente) no copo A.
c) mergulhar o copo B em água gelada
(inferior à temperatura ambiente) e deixar o
copo A sem líquido.
d) encher o copo A com água quente (superior
à temperatura ambiente) e mergulhar o copo
B em água gelada (inferior à temperatura
ambiente).
Página 26 de 31
e) encher o copo A com água gelada (inferior
à temperatura ambiente) e mergulhar o copo
B em água quente (superior à temperatura
ambiente).
5. Com relação à dilatação dos sólidos e
líquidos isotrópicos, analise as proposições a
seguir e dê como resposta a soma dos números
associados às afirmações corretas.
(01) Um recipiente com dilatação desprezível
contém certa massa de água na
temperatura de 1C, quando é, então,
aquecido lentamente, sofrendo uma
variação de temperatura de 6C. Nesse
caso, o volume da água primeiro aumenta
e depois diminui.
(02) Quando se aquece uma placa metálica que
apresenta um orifício, verifica-se que, com
a dilatação da placa, a área do orifício
aumenta.
(03) Quando um frasco completamente cheio
de líquido é aquecido, este transborda um
pouco. O volume de líquido transbordado
mede a dilatação absoluta do líquido.
(04) O vidro pirex apresenta maior resistência
ao choque térmico do que o vidro comum
porque tem menor coeficiente de dilatação
térmica do que o vidro comum.
(05) Sob pressão normal, quando uma massa
de água é aquecida de 0 C até 100C
sua densidade sempre aumenta.
(06) Ao se elevar a temperatura de um sistema
constituído por três barras retas e
idênticas de ferro interligadas de modo a
formarem um triângulo isósceles, os
ângulos internos desse triângulo não se
alteram.
a) 07.
b) 10.
c) 11.
d) 12.
6.
Duas barras metálicas,
α Y  2α X , assinale a alternativa
que indica a reta que melhor representa o
acréscimo  / no comprimento da barra Y,
Sabendo que
em função da variação da temperatura.
a) 1
b) 2
c) 3
d)
e)
4
5
7. Num laboratório, um grupo de alunos
registrou o comprimento L de uma barra
metálica, à medida que sua temperatura T
aumentava, obtendo o gráfico abaixo:
X e Y, mesmo
comprimento (I) em temperatura ambiente
T0 , são aquecidas uniformemente até uma
temperatura T. Os materiais das barras têm
coeficientes de dilatação linear,
respectivamente α X e a Y , que são positivos e
Pela análise do gráfico, o valor do coeficiente de
dilatação do metal é
5 1
a) 1,05  10 C
podem ser considerados constantes no intervalo
de temperatura T  T  T0 .
b)
1,14  105 C1
Na figura abaixo, a reta tracejada X
representa o acréscimo relativo  / no
comprimento da barra X, em função da
c)
1,18  105 C1
d)
1,22  105 C1
e)
1,25  105 C1
variação da temperatura.
8. A tabela a seguir apresenta os coeficientes
de dilatação linear de alguns metais:
Metais
Coeficiente de dilatação linear
1
ferro
12  10 6
cobre
17  10 6
alumínio
22  106
(C )
Página 27 de 31
26  106
zinco
Uma placa de metal de área
aquecida até atingir
variação de
1m2 a 20C é
100C apresentando uma
35,2cm2 em sua área. O metal
que constitui essa placa é o
a) ferro.
b) cobre.
c) zinco.
d) alumínio.
9. Ao lavar pratos e copos, um cozinheiro
verifica que dois copos estão encaixados
firmemente, um dentro do outro. Sendo o copo
externo feito de alumínio e o interno, de vidro,
sobre as formas de separá-los, utilizando os
princípios básicos de dilatação térmica, analise
os itens a seguir:
I. Aquecendo apenas o copo de vidro.
II. Esfriando apenas o copo de alumínio.
III. Aquecendo ambos.
IV. Esfriando ambos.
Dados: os coeficientes de dilatação térmica do
alumínio e do vidro são iguais a
aAl  24  106 C1 e
avidro  0,5  106 C1, respectivamente.
Está(ão) CORRETO(S) apenas
a) I e II.
b) I.
c) II.
d) III.
e) IV.
10. Uma longa ponte foi construída e instalada
com blocos de concreto de 5 m de comprimento
a uma temperatura de 20°C em uma região na
qual a temperatura varia ao longo do ano entre
10°C e 40°C. O concreto destes blocos tem
coeficiente de dilatação linear de 10-5°C-1.
Nessas condições, qual distância em cm deve
ser resguardada entre os blocos na instalação
para que, no dia mais quente do verão, a
separação entre eles seja de 1 cm?
a) 1,01
b) 1,10
c) 1,20
d) 2,00
e) 2,02
Dinâmica
O sistema representado na figura acima
corresponde a um corpo 1, com massa 20 kg,
apoiado sobre uma superfície plana horizontal,
e um corpo 2, com massa de 6 kg, o qual está
apoiado em um plano inclinado que faz 60
com a horizontal. O coeficiente de atrito
cinético entre cada um dos corpos e a superfície
de apoio é 0,1 Uma força F de 200 N, aplicada
sobre o corpo 1, movimenta o sistema, e um
sistema que não aparece na figura faz com que
a direção da força F seja mantida constante e
igual a 30 em relação à horizontal. Uma
corda inextensível e de massa desprezível une
os dois corpos por meio de uma polia.
Considere que a massa e todas as formas de
atrito na polia são desprezíveis. Também
considere, para esta questão, a aceleração
2
gravitacional como sendo de 10 m s e o
cos 30 igual a 0,87. Com base nessas
informações, assinale a alternativa que
apresenta a tensão na corda que une os dois
corpos.
a) 12,4 N.
b)
48,4 N.
c) 62,5 N.
d) 80,3 N.
e) 120,6 N.
2.
120 kg, atua
uma força horizontal constante F de
intensidade 600 N. A caixa encontra-se sobre
uma superfície horizontal em um local no qual a
2
aceleração gravitacional é 10 m s . Para que
a aceleração da caixa seja constante, com
2
módulo igual a 2 m s . e tenha a mesma
orientação da força
F,
o coeficiente de atrito
cinético entre a superfície e a caixa deve ser de
a) 0,1
b)
1.
Sobre uma caixa de massa
c)
d)
e)
0,2
0,3
0,4
0,5
3. Uma caixa encontra-se em repouso em
relação a uma superfície horizontal. Pretendese colocar essa caixa em movimento em
relação a essa superfície. Para tal, será aplicada
Página 28 de 31
uma força de módulo F que forma 53 acima
da direção horizontal. Considerando que o
coeficiente de atrito estático entre a superfície
da caixa e a superfície horizontal é igual a
0,25, que o coeficiente de atrito dinâmico
entre a superfície da caixa e a superfície
horizontal é igual a 0,10, que a massa do
objeto é igual
2 kg e que a aceleração da
gravidade no local é igual a
10 m s2 , o menor
módulo da força F que deverá ser aplicado
para mover a caixa é um valor mais próximo de
Utilize:
sen 53  0,8 e cos 53  0,6
a)
6,25 N
b) 8,33 N
c) 12,50 N
d) 20,00 N
4. Para se calcular o coeficiente de atrito
dinâmico entre uma moeda e uma chapa de
fórmica, a moeda foi colocada para deslizar pela
chapa, colocada em um ângulo de 37 com a
horizontal.
Foi possível medir que a moeda, partindo do
repouso, deslizou 2,0 m em um intervalo de
tempo de
b) Mesmo sem ser realizada uma medida para o
atrito estático, o valor do coeficiente desse
atrito será menor do que o encontrado para
o atrito cinético em cada caso.
c) O tênis B possui maior coeficiente de atrito
cinético do que o tênis A.
d) Foi determinado um valor de 0,6 para o
coeficiente de atrito cinético para o tênis B.
e) Em nenhuma das medidas foi determinado
um valor maior ou igual a 0,7.
6. Em um filme de ficção científica, uma nave
espacial possui um sistema de cabines girantes
que permite ao astronauta dentro de uma
cabine ter percepção de uma aceleração similar
à gravidade terrestre. Uma representação
esquemática desse sistema de gravidade
artificial é mostrada na figura a seguir. Se, no
espaço vazio, o sistema de cabines gira com
uma velocidade angular ω, e o astronauta
dentro de uma delas tem massa
m, determine
o valor da força normal exercida sobre o
astronauta quando a distância do eixo de
rotação vale R. Considere que R é muito
maior que a altura do astronauta e que existe
atrito entre o solo e seus pés.
1,0 s, em movimento uniformemente
variado.
g  10 m s2 , sen 37  0,60 e
cos 37  0,80.
Adote
Nessas condições, o coeficiente de atrito
dinâmico entre as superfícies vale
a) 0,15.
b)
c)
d)
e)
0,20.
0,25.
0,30.
0,40.
5. Um professor de ensino médio deseja
determinar o coeficiente de atrito cinético entre
dois tênis e o chão dos corredores da escola,
supostamente horizontais. Para tanto, ele mede
inicialmente a massa dos dois tênis, A e B,
encontrando um valor de 400 g e 500 g,
respectivamente. Após, solicita que um aluno
puxe horizontalmente os tênis com um
dinamômetro, verificando a sua marcação
quando o tênis está se movendo com
velocidade constante, sendo que são
registrados os valores de 2,8 N para o tênis A
e
a)
mRω2
b)
2mRω2
c)
mRω2 2
d)
mω2 R
e)
8mRω2
7. Um satélite esférico, homogêneo e de
massa m, gira com velocidade angular
constante em torno de um planeta esférico,
homogêneo e de massa M, em uma órbita
circular de raio
R e período T, conforme
figura abaixo. Considerando G a constante de
gravitação universal, a massa do planeta em
função de R, T e G é:
3,0 N para o tênis B.
Com base nessas informações e considerando a
2
aceleração da gravidade igual a 10 m / s , é
correto afirmar que:
a) O coeficiente de atrito cinético determinado
para o tênis A é um valor entre 0,4 e 0,6.
Página 29 de 31
d)
e)
16 m
20 m
9.
Considere que um satélite de massa
m  5,0 kg seja colocado em órbita circular ao
redor da Terra, a uma altitude h  650 km.
Sendo o raio da Terra igual a 6.350 km, sua
5,98  1024 kg e a constante de
massa igual a
gravitação universal
11
G  6,67  10
quantidade de movimento do satélite, em
kg  m s, é, aproximadamente, igual a
4 π 2 R3
a)
TG
b)
c)
2
2
2
2
4π R
TG
4π R
2
T G
2
d)
e)
8.
4π R
4 π 2 R3
Um corpo de massa
300 kg é abandonado,
a partir do repouso, sobre uma rampa no ponto
A, que está a 40 m de altura, e desliza sobre
percorre
7,6  103
b)
3,8  104
c)
8,0  104
d)
2,8  1011
e)
5,6  1011
objeto pontual O está submetido a uma força
de módulo 16,0N, resultando em uma
T2 G
a rampa
a)
10. No instante mostrado na figura a seguir, o
cabo elástico está tensionado com uma tração
de módulo igual a 36,0N, ao passo que o
T2 G
a rampa até o ponto
N  m2 kg2 , o módulo da
B,
aceleração de módulo
2,0 m / s2 que aponta
para a direita.
sem atrito. Ao terminar
AB, ele continua o seu movimento e
40 m de um trecho plano e horizontal
BC com coeficiente de atrito dinâmico de
0,25 e, em seguida, percorre uma pista de
formato circular de raio R, sem atrito,
conforme o desenho abaixo. O maior raio R
que a pista pode ter, para que o corpo faça
todo trajeto, sem perder o contato com ela é de
Dado: intensidade da aceleração da gravidade
2
g  10 m / s
Sabendo que a massa do objeto
O é igual a
m  2,0kg e desprezando efeitos
gravitacionais, é CORRETO afirmar que o valor
do ângulo θ
a) está entre
10 e 20
b) é exatamente igual a
c) está entre
30
30 e 60
d) é exatamente igual a
e) está entre
11.
60
60 e 90
Um bloco metálico de massa
2,0 kg é
lançado com velocidade de 4,0 m / s a partir
da borda de um trilho horizontal de
comprimento 1,5 m e passa a deslizar sobre
a)
b)
8m
10 m
c) 12 m
esse trilho. O coeficiente de atrito cinético entre
as superfícies vale 0,2. Cada vez que colide
com as bordas, o disco inverte seu movimento,
Página 30 de 31
mantendo instantaneamente o módulo de sua
velocidade.
entre blocos, nas situações I e II, é,
respectivamente,
a) F / 4 e F / 4.
b) F / 4 e 3F / 4.
c)
d)
Quantas vezes o disco cruza totalmente o
trilho, antes de parar?
Considere:
a)
b)
c)
d)
e)
F / 2 e F / 2.
3F / 4 e F / 4.
e) F e F.
g  10 m / s2
0
1
2
3
4
12.
Um bloco
B de massa 400g está
A de massa 800g, o
apoiado sobre um bloco
qual está sobre uma superfície horizontal. Os
dois blocos estão unidos por uma corda
inextensível e sem massa, que passa por uma
polia presa na parede, conforme ilustra abaixo.
O coeficiente de atrito cinético entre os dois
blocos e entre o bloco A e a superfície
horizontal é o mesmo e vale 0,35.
Considerando a aceleração da gravidade igual a
10m / s2 e desprezando a massa da polia,
assinale a alternativa correta para o módulo da
força F necessária para que os dois blocos se
movam com velocidade constante.
a)
b)
c)
d)
e)
1,4N.
4,2N.
7,0N.
8,5N.
9,3N.
13. Dois blocos, 1 e 2, são arranjados de duas
maneiras distintas e empurrados sobre uma
superfície sem atrito, por uma mesma força
horizontal F. As situações estão representadas
nas figuras I e II abaixo.
Considerando que a massa do bloco 1 é
que a massa do bloco 2 é
m1 e
m2  3m1, a opção
que indica a intensidade da força que atua
Página 31 de 31