Aula 5 Ótica geométrica

Aula 5
Ótica geométrica
Referência: E. Hecht, óptica, Fundação Calouste Gulbekian, segunda edição portuguesa (2002);
objeto
P
S
imagem
Sistema ótico
Fonte pontual
Sempre que a cada feixe de raios que diverge a partir de S, corresponde a um
feixe de raios que converge para P, o sistema ótica diz-se estigmático para os
pontos S e P.
S e P constituem um par de pontos conjugados
Na prática, ocorre sempre um desvio inevitável da direção de propagação
retilínea (difração). Num sistema ótico real o grau máximo de perfeição possível
de atingir na formação de imagens é limitado por difração.
No limite teórico de λ→0, é possível recuperar a propagação retilínea da luz: é o
domínio da ótica geométrica
LENTES
n2 > n1
REFRAÇÃO EM SUPERFÍCIES ESFÉRICAS
s
P
n2
n1
Qual é a forma da interface, de modo que a onda no segundo meio, convirja para
P, formando uma imagem perfeita de S ?
O tempo que cada parte da frente de onda leva de S até P deve ser sempre o
mesmo (Huygens, 1678)
Principio de Fermat: o percurso ótico medido sobe raios luminosos entre S e P
defletidos em pontos A da interface é o mesmo para todos os raios.
vértice
A
li
lo
eixo ótico
V
P
S
so
n1
distância objeto
si
distância imagem
n2
lon1 +lin2 = son1 + sin2 = constante
(equação oval de Descartes)
Para além da focalização de ondas esférica, as interfaces refrigentes (dioptros),
permitem efetuar outros tipos de manipulações a forma das frentes de onda.
n1
n
1
n2
n2
elipsóides
Todas estas considerações foram desenvolvidas por Descartes. Foi
Kepler quem sugeriu em 1611 a utilização de seções cônicas para
constituição de lentes e espelhos
n2 > n1
Elementos óticos com dioptros que não são esféricos nem planos, são
conhecidos como asféricos. Embora o seu funcionamento seja fácil de
compreender e realizem muito bem certas funções, as lentes asféricas são
bastante difíceis de produzir com precisão; todavia sempre que os custos o
justificam as lentes asféricas são utilizadas.
Lentes esféricas
Vantagens:
Mais fáceis de fabricar do que as lentes asféricas
Custo!
Desvantagens:
As aberrações estão sempre presentes, mas já se consegue fabricar
Lentes com aberrações controladas ao limite da difração.
Refração num dioptro esférico
θr
θi
lo
n2
A
h
R
V
li
θt
ϕ
C
S
so
si
n2 > n1
n1
P
θt < θi
Convenção de sinais para dióptricos esféricos e lentes delgadas
so , fo
+ à esquerda de V
xo
+ à esquerda de Fo
s i , fi
+ à direita de V
xi
+ à direita de Fo
R
+ se C estiver à direita de V
yo , yi
+ acima do eixo ótico
(inclui grandezas ainda não referidas)
Lei dos co-senos aplicada aos triângulos SAC e ACP e na relação cosϕ = cos(π -ϕ)
lo = R 2 + ( so + R ) 2 − 2 R ( so + R ) cos ϕ
li = R 2 + ( si − R ) 2 − 2 R( si − R ) cos ϕ
θi
lo
θr
A
h
V
n2
li
R θt
ϕ
C
S
so
si
P
O percurso ótico (PO) é dado por:
PO = n1lo + n2 li
PO = n1 R 2 + ( so + R ) 2 − 2 R( so + R ) cos ϕ + n2 R 2 + ( si − R ) 2 + 2 R ( si − R ) cos ϕ
Quando o ponto A se desloca sobre o dióptrico (com R=cte), o ângulo ϕ pode
ser utilizado para parametrizar a posição de A, logo, fazendo d(PO)/dϕ = 0
(principio de Fermat):
n1 R( so + R ) senϕ n2 R( si − R ) senϕ
−
=0
2l o
2l i
E após rearranjo...
n1 n2 1  n2 si n1 so 

+
= 
−
lo
li
R  li
lo 
Variando ϕ, o novo raio não intercepta o eixo ótico em P – aberração esférica
n1 n2 1  n2 si n1 so 

+
= 
−
lo
li
R  li
lo 
Quando ϕ é pequeno, cosϕ ≅1 e senϕ≅ϕ, logo
lo = R 2 + ( so + R ) 2 − 2 R( so + R ) cos ϕ ≈ so
li = R 2 + ( si − R ) 2 − 2 R ( si − R ) cos ϕ ≈ si
n1 n2 1  n2 si n1 so 

+
= 
−
lo
li
R  li
lo 
Simplifica como:
n1 n2  n2 − n1 
+
=

so si  R 
Esta aproximação de primeira ordem (senϕ ≅ ϕ) delimita o domínio da ótica
geométrica de primeira ordem ou paraxial.
Os raios que se propagam muito próximos ao eixo ótico são designados de
raios paraxiais.
A frente de onda emergente associada a estes raios paraxiais é
essencialmente esférica e dá origem a uma imagem “perfeita” em P.
Em 1841,Gauss contruiu uma análise da formação de imagens nesta
aproximação , e que é conhecida por ótica Gaussiana, paraxial ou de
primeira ordem.
Se a imagem do ponto Fo se formar no infinito (si = ∞) então:
n1 n2  n2 − n1 
+
=

so ∞  R 
Fo
so = fo
n1
fo =
R
n2 − n1
Distância focal objeto
Se a imagem do ponto Fi se formar no infinito (so = ∞) então:
n1 n2  n2 − n1 
+
=

∞ si  R 
si = fi
n2
fi =
R
n2 − n1
Distância focal imagem
f i ≠ fo
Fi
Lentes delgadas
Índice da lente
Índice do meio
n m n l  nl − n m 

+
= 
so1 si1  R1 
Posição do objeto
Posição da imagem
Se so < fo si torna-s negativo (virtual)
Primeiro dióptro
Segundo dióptro
n m n l  nl − n m 

+
= 
so1 si1  R1 
n m nl  n m − n l
+
= 
si 2 s02  R2
P
P’
S
C2
V1
V2
R1
R2
so1
si1
C1
d
si2
so2



| so2 | = | si1 | + d
Pela convenção de sinais:
so2 = - si1 + d
P
P’
S
C2
V1
V2
R1
R2
so1
si1
C1
d
si2
so2
Somando as equações para o primeiro e segundo dióptro:
 1
nm nm
nl d
1 
 +
+
= ( nl − nm ) −
so1 si 2
 R1 R2  (si1 − d )si1
Para lentes delgadas d→0 e o último termo do segundo membro se anula.
No ar, nm ≈ 1:
 1
1 1
1 

+ = ( nl − 1) −
so si
 R1 R2 
Equação das lentes delgadas!
 1
1 1
1 

+ = ( nl − 1) −
so si
 R1 R2 
lim so →∞ si = f i ↔ lim si→∞ so = f o
fi = fo
 1
1
1 

= ( nl − 1) −
f
 R1 R2 
1
1 1
= +
f
so si
Fórmula de Gauss
Associação de lentes delgadas
...
f1
f2
f3
fn
Distância focal efetiva para lentes em contacto ou coladas
1/f = 1/f1 +1/f2 + 1/f3 + ... + 1/fn
Potência dióptrica
D = 1/f→ D = D1 +D2 + D3 + ...+ Dn
Quando fazemos um feixe de luz atravessar duas lentes consecutivas,
temos uma associação de lentes que possui um foco efetivo dado por:
1
1
1
d
=
+
−
f
f1 f 2 f1 f 2
d
O olho humano
A zona de junção do nervo ótico com o olho é insensível à luz pois não
contém qualquer célula receptora; tem o nome de ponto cego.
SIMAS, Maria Lúcia de Bustamante;
SANTOS, Natanael Antonio dos. O
fenômeno de muitas-faces: investigações
preliminares. Psicol. Reflex. Crit., Porto
Alegre, v. 18, n. 1, Apr. 2005 .
O ponto mais afastado para o qual é possível a visão distinta é chamado ponto
remoto
A distância mínima de visão distinta é dada pelo ponto próximo.
Idade (anos)
Ponto próximo (cm)
10
7
20
10
30
14
40
22
50
40
60
200
A lupa, microscópio simples ou lente de aumento
O tamanho aparente de um objeto é determinado pelo tamanho de sua
imagem na retina, o qual, por sua vez, a olho nú, depende do ângulo
subtendido pelo objeto.
y
θ
P≈ 25 cm
Ponto próximo
Quando se quer examinar detalhadamente um objeto diminuto, coloca-se
o mesmo próximo ao ôlho, afim de que o ângulo subtendido seja o maior
possível.
Imagem virtual
θ’
y
so
≈ 25 cm
Colocando uma lente convergente em frente à vista, a acomodação pode ser
aumentada; o objeto fica, então, situado aquém do ponto próximo, e
subtende,portanto, um ângulo maior.
O aumento M da lupa (que não deve ser confundido com amplificação) é
definido como a relação entre os ângulos θ’ e θ:
θ≈ y/25
Usando 1/so + 1/si = 1/f
si = -25 cm
so = 25f/(25 + f)
θ’ ≈ y/so
M = θ’/ θ = (25/f) + 1
Se a imagem é formada no infinito (si = ∞), so = f
M = 25/f
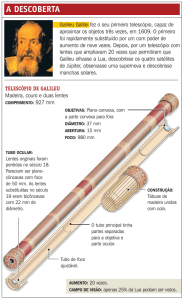
O telescópio
Não se sabe ao certo a quem se deve a invenção do telescópio- foi
provavelmente inventado e reinventado várias vezes.
O telescópio (luneta astronômica)
A luneta astronômica é usada na observação de objetos distantes, que são
grandes mas nos parecem pequenos por estarem muito distantes de nós. Na
sua forma mais simples é, como o microscópio, constituída por um tubo com
uma lente em cada extremidade.
objetiva
Imagem real
ocular
F’2 ,F1
θ
θ’
θ
y’
f
F’1
f’
Imagem virtual no infinito
tgθ≈θ=y´/f
tgθ’≈θ’=y´/f’
MA = θ’/θ =f/f’
Na prática a posição da imagem intermediária é fixa e a focagem se faz por
deslocamento da ocular