(UFRGS) O gráfico abaixo apresenta a evolução da emissão de

b)
c)
d)
e)
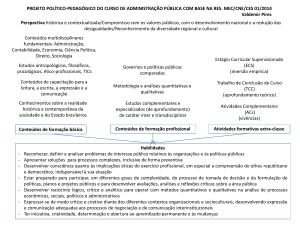
01. (UFRGS) O gráfico abaixo apresenta a evolução da
emissão de Dióxido de carbono ao longo dos anos.
a)
b)
c)
d)
e)
Com base nos dados do gráfico, assinale a alternativa
correta.
Ao longo do período, a emissão de dióxido de carbono
apresentou crescimento constante.
Em relação aos anos 80, os anos 90 apresentaram
emissão de dióxido de carbono 30% maior.
O ano de 2009 apresentou menor valor de emissão de
dióxido de carbono da primeira década do século XXI.
De 2000 a 2013, houve crescimento percentual de
11,7% na emissão de dióxido de carbono.
Em relação a 2000, o ano de 2013 apresentou emissão
de dióxido de carbono aproximadamente 50% maior.
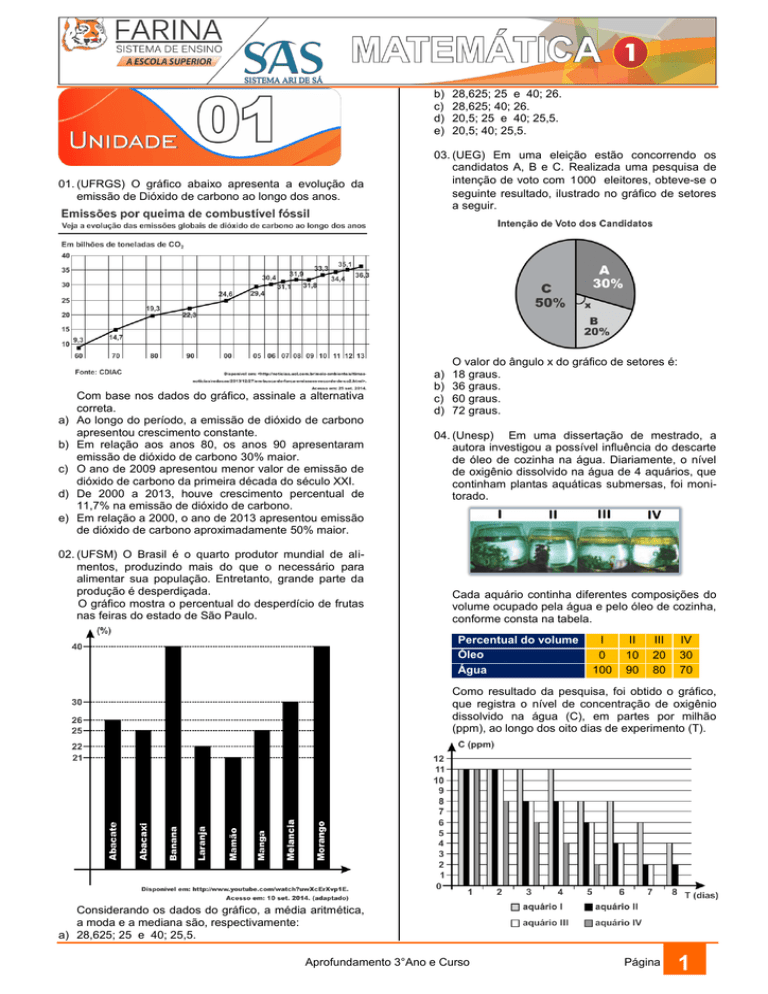
02. (UFSM) O Brasil é o quarto produtor mundial de alimentos, produzindo mais do que o necessário para
alimentar sua população. Entretanto, grande parte da
produção é desperdiçada.
O gráfico mostra o percentual do desperdício de frutas
nas feiras do estado de São Paulo.
28,625; 25 e 40; 26.
28,625; 40; 26.
20,5; 25 e 40; 25,5.
20,5; 40; 25,5.
03. (UEG) Em uma eleição estão concorrendo os
candidatos A, B e C. Realizada uma pesquisa de
intenção de voto com 1 000 eleitores, obteve-se o
seguinte resultado, ilustrado no gráfico de setores
a seguir.
a)
b)
c)
d)
O valor do ângulo x do gráfico de setores é:
18 graus.
36 graus.
60 graus.
72 graus.
04. (Unesp) Em uma dissertação de mestrado, a
autora investigou a possível influência do descarte
de óleo de cozinha na água. Diariamente, o nível
de oxigênio dissolvido na água de 4 aquários, que
continham plantas aquáticas submersas, foi monitorado.
Cada aquário continha diferentes composições do
volume ocupado pela água e pelo óleo de cozinha,
conforme consta na tabela.
Percentual do volume
Óleo
Água
I
0
100
II
10
90
III
20
80
IV
30
70
Como resultado da pesquisa, foi obtido o gráfico,
que registra o nível de concentração de oxigênio
dissolvido na água (C), em partes por milhão
(ppm), ao longo dos oito dias de experimento (T).
Considerando os dados do gráfico, a média aritmética,
a moda e a mediana são, respectivamente:
a) 28,625; 25 e 40; 25,5.
Aprofundamento 3°Ano e Curso
Página
1
a)
b)
c)
d)
e)
Tomando por base os dados e resultados apresentados, é correto afirmar que, no período e nas condições
do experimento:
Não há dados suficientes para se estabelecer o nível
de influência da quantidade de óleo na água sobre o
nível de concentração de oxigênio nela dissolvido.
Quanto maior a quantidade de óleo na água, maior a
sua influência sobre o nível de concentração de oxigênio nela dissolvido.
Quanto menor a quantidade de óleo na água, maior a
sua influência sobre o nível de concentração de oxigênio nela dissolvido.
Quanto maior a quantidade de óleo na água, menor a
sua influência sobre o nível de concentração de oxigênio nela dissolvido.
Não houve influência da quantidade de óleo na água
sobre o nível de concentração de oxigênio nela dissolvido.
07. (Fuvest) Cada uma das cinco listas dadas é a
relação de notas obtidas por seis alunos de uma
turma em uma certa prova.
Assinale a única lista na qual a média das notas é
maior do que a mediana.
a) 5; 5; 7; 8; 9; 10.
b) 4; 5; 6; 7; 8; 8.
c) 4; 5; 6; 7; 8; 9.
d) 5; 5; 5; 7; 7; ; 9.
e) 5; 5; 10; 10; 10; 10.
08. (Unifor) O diretor de um curso de Inglês resolve
montar as turmas fazendo uma distribuição por
idade dos alunos do curso. O gráfico abaixo representa a quantidade de alunos por idade.
05. (UPE) O quadro abaixo mostra o número de gols marcados em cada uma das partidas do grupo do Brasil na
primeira fase da Copa do Mundo de 2014.
Partida
Brasil x Croácia
México x Camarões
Brasil x México
Croácia x Camarões
Camarões x Brasil
Croácia x México
a)
b)
c)
d)
e)
Gols Marcados
4
1
0
4
5
4
O desvio médio de gols marcados por partida nos jogos
desse grupo foi de, aproximadamente:
3,0.
2,0.
1,7.
1,5.
1,2.
06. (UFPR) O gráfico abaixo representa a quantidade
aproximada de animais adotados ao longo de cinco
anos em uma determinada cidade.
a)
b)
c)
d)
e)
Qual a porcentagem de alunos que irá formar uma
turma com idade de 16 e 17 anos?
20%.
30%.
45%.
55%.
65%.
09. (UPE) Numa competição esportiva, cinco atletas
estão disputando as três primeiras colocações da
prova de salto em distância. A classificação será
pela ordem decrescente da média aritmética de
pontos obtidos por eles, após três saltos consecutivos na prova. Em caso de empate, o critério adotado será a ordem crescente do valor da variância.
A pontuação de cada atleta está apresentada na
tabela a seguir:
Atleta
A
B
C
D
E
a)
b)
c)
d)
e)
Qual foi a média anual de animais adotados, ao longo
dos cinco anos nessa cidade?
350.
380.
390.
410.
440.
a)
b)
c)
d)
e)
Pontuação
1º Salto
6
7
5
4
5
Pontuação
2º Salto
6
3
7
6
8
Pontuação
3º Salto
6
8
6
8
5
Com base nas informações apresentadas, o primeiro, o segundo e o terceiro lugares dessa prova
foram ocupados, respectivamente, pelos atletas
A; C; E.
B; D; E.
E; D; B.
B; D; C.
A; B; D.
Aprofundamento 3°Ano e Curso
Página
2
10. (ENEM) Os candidatos K, L, M, N e P estão disputando
uma única vaga de emprego em uma empresa e fizeram provas de português, matemática, direito e informática. A tabela apresenta as notas obtidas pelos cinco
candidatos.
Candidato
K
L
M
N
P
a)
b)
c)
d)
e)
Português
33
32
35
24
36
Matemática
33
39
35
37
16
Direito
33
33
36
40
26
Informática
34
34
34
35
41
01. (UEMG) Observe a tirinha abaixo:
Segundo o edital de seleção, o candidato aprovado será aquele para o qual a mediana das notas obtidas por
ele nas quatro disciplinas for a maior.
O candidato aprovado será
K.
L.
M.
N.
P.
a)
b)
c)
d)
Passando por uma sorveteria, Magali resolve parar
e pedir uma casquinha. Na sorveteria, há 6 sabores diferentes de sorvete e 3 é o número máximo
de bolas por casquinha, sendo sempre uma de cada sabor.
O número de formas diferentes com que Magali
poderá pedir essa casquinha é igual a
20.
41.
120.
35.
02. (UECE) A turma K do Curso de Administração da
UECE é formada por 36 alunos, sendo 22 mulheres e 14 homens. O número de comissões que podem ser formadas com alunos desta turma, tendo
cada comissão três componentes e sendo assegurada a participação de representantes dos dois sexos em cada comissão, é:
a) 5 236 .
b) 6 532 .
c) 3 562 .
d) 2 635 .
GABARITO
01. E
02. A
03. D
04. B
05. C
06. D
07. D
08. C
09. A
10. D
03. (PUC-RS) Um fotógrafo foi contratado para tirar
fotos de uma família composta por pai, mãe e quatro filhos. Organizou as pessoas lado a lado e colocou os filhos entre os pais. Mantida essa configuração, o número de formas em que poderão se
posicionar para a foto é:
a) 4.
b) 6.
c) 24.
d) 36.
e) 48.
Aprofundamento 3°Ano e Curso
Página
3
04. (UPE) A vendedora de roupas está arrumando os cabides da vitrine de uma loja. Ela deve pendurar 5 camisas, 3 bermudas e 2 casacos na vitrine, de modo que
cada peça fique uma do lado da outra sem sobreposição.
Quantas são as disposições possíveis nessa arrumação, de modo que as peças de um mesmo tipo fiquem
sempre juntas, lado a lado na vitrine?
a) 30.
b) 120.
c) 1 440.
d) 4 320.
e) 8 640.
05. (UERJ) Uma criança ganhou seis picolés de três sabores diferentes: baunilha, morango e chocolate, representados, respectivamente, pelas letras B, M e C. De
segunda a sábado, a criança consome um único picolé
por dia, formando uma sequência de consumo dos sabores. Observe estas sequências, que correspondem a
diferentes modos de consumo:
a)
b)
c)
d)
O número total de modos distintos de consumir os picolés equivale a:
6.
90.
180.
720.
06. (Unicamp) O número mínimo de pessoas que deve
haver em um grupo para que possamos garantir que
nele há pelo menos três pessoas nascidas no mesmo
dia da semana é igual a:
a) 21.
b) 20.
c) 15.
d) 14.
07. (UERJ) Considere o código abaixo, que identifica
determinado produto.
a)
b)
c)
d)
Esse código corresponde ao seguinte número:
6 835.
5 724.
8 645.
9 768.
08. (UEMG) Na Copa das Confederações de 2013, no
Brasil, onde a seleção brasileira foi campeã, o técnico Luiz Felipe Scolari tinha à sua disposição 23
jogadores de várias posições, sendo: 3 goleiros, 8
defensores, 6 meio-campistas e 6 atacantes. Para
formar seu time, com 11 jogadores, o técnico utiliza 1 goleiro , 4 defensores , 3 meio-campistas e 3
atacantes. Tendo sempre Júlio César como goleiro
e Fred como atacante, o número de times distintos
que o técnico poderá formar é:
a) 14 000.
b) 480.
c) 8! + 4!
d) 72 000.
09. (Unesp) Um professor, ao elaborar uma prova
composta de 10 questões de múltipla escolha, com
5 alternativas cada e apenas uma correta, deseja
que haja um equilíbrio no número de alternativas
corretas, a serem assinaladas com X na folha de
respostas. Isto é, ele deseja que duas questões
sejam assinaladas com a alternativa A, duas com
a B, e assim por diante, como mostra o modelo.
Modelo de folha de resposta (gabarito)
A
01
B
X
04
05
X
X
07
X
08
10
Observe um exemplo de código e de seu número correspondente:
X
06
09
a)
b)
c)
d)
e)
E
X
03
Uma loja identifica seus produtos com um código que
utiliza 16 barras, finas ou grossas. Nesse sistema de codificação, a barra fina representa o zero e a grossa o 1. A
conversão do código em algarismos do número correspondente a cada produto deve ser feita de acordo com esta
tabela:
D
X
02
Texto Para a Questão 07
C
X
X
X
Nessas condições, a quantidade de folha de respostas diferentes, com a letra X disposta nas alternativas corretas, será:
302 400.
113 400.
226 800.
181 440.
604 800.
Aprofundamento 3°Ano e Curso
Página
4
10. (Enem) Um cliente de uma videolocadora tem o hábito
de alugar dois filmes por vez. Quando os devolve,
sempre pega outros dois filmes e assim sucessivamente. Ele soube que a videolocadora recebeu alguns lançamentos, sendo 8 filmes de ação, 5 de comédia e 3
de drama e, por isso, estabeleceu uma estratégia para
ver todos esses 16 lançamentos. Inicialmente alugará,
em cada vez, um filme de ação e um de comédia.
Quando se esgotarem as possibilidades de comédia, o
cliente alugará um filme de ação e um de drama, até
que todos os lançamentos sejam vistos e sem que nenhum filme seja repetido.
De quantas formas distintas a estratégia desse cliente
poderá ser posta em prática?
a) 20  8!(3! )2 .
b) 8!5!3! .
8!5!3!
c)
.
28
8!5!3!
d)
.
22
16!
e)
.
28
01. (Unesp) Uma loja de departamentos fez uma pesquisa de opinião com 1 000 consumidores, para
monitorar a qualidade de atendimento de seus
serviços. Um dos consumidores que opinaram foi
sorteado para receber um prêmio pela participação
na pesquisa.
A tabela mostra os resultados percentuais registrados na pesquisa, de acordo com as diferentes
categorias tabuladas.
Categorias
Ótimo
Regular
Péssimo
Não Opinaram
a)
b)
c)
d)
e)
GABARITO
01. B
02. A
03. E
04. E
05. B
06. C
07. A
08. A
09. B
10. B
Percentuais
25
43
17
15
Se cada consumidor votou uma única vez, a probabilidade de o consumidor sorteado estar entre
os que opinaram e ter votado na categoria péssimo é, aproximadamente:
20%.
30%.
26%.
29%.
23%.
02. (PUC-PR) Um agricultor adquiriu 60 sementes de
milho para fazer o plantio, com a garantia de que a
probabilidade de germinação é de 0,8 (independentes das outras). Ao utilizar a plantadeira manual, não percebeu que havia uma semente utilizada
na safra anterior com probabilidade de germinação
de 0,5 e esta se misturou às novas sementes. Assim, o agricultor plantou as 61 sementes e destas,
60 germinaram. Dado que a probabilidade de uma
97
semente germinar (velha ou nova) é de
, qual
122
é a probabilidade de que a semente que não germinou tenha sido uma das sementes novas?
24
a)
.
25
71
b)
.
122
60
c)
.
61
1
d)
.
51
1
e)
.
122
03. (UEMG) Em uma empresa, foi feita uma préseleção para sorteio de uma viagem. Esta préseleção se iniciou com a distribuição, entre os funcionários, de fichas numeradas de 1 a 23. Em seguida, foram selecionados os funcionários com as
fichas numeradas, com as seguintes regras:
Fichas com um algarismo: o algarismo tem que ser
primo;
Aprofundamento 3°Ano e Curso
Página
5
a)
b)
c)
d)
Fichas com dois algarismos: a soma dos algarismos
deverá ser um número primo.
Após essa pré-seleção, Glorinha foi classificada para o
sorteio.
A probabilidade de Glorinha ganhar essa viagem no
sorteio é de, aproximadamente:
7%.
8%.
9%.
10%.
07. (UFSM) A tabela a seguir mostra o número de
internações hospitalares da população idosa (60
ou mais anos de idade), numa determinada região,
de acordo com as causas da internação.
Causas
Doenças Cardíacas
Doenças Cerebrovasculares
Doenças Pulmonares
Doenças Renais
Diabetes Melito
Fraturas de Fêmur e
Ossos dos Membros
Hipertensão Arterial
Infecção de Pele e
Tecido Subcutâneo
Pneumonia Bacteriana
Úlcera
04. (UEG) A tabela a seguir apresenta a preferência de
homens e mulheres em relação a um prato, que pode
ser doce ou salgado, típico de certa região do Estado
de Goiás.
Sexo
Masculino
Feminino
a)
b)
c)
d)
Preferências
Doce Salgados
80
20
60
40
Considerando-se os dados apresentados na tabela, a
probabilidade de um desses indivíduos preferir o prato
típico doce, sabendo-se que ele é do sexo feminino, é
de:
0,43.
0,50.
0,60.
0,70.
05. (PUC-RJ) Em uma urna existem 10 bolinhas de cores
diferentes, das quais sete têm massa de 300 gramas
as cada e as outras três têm massa de 200 gramas
cada. Serão retiradas 3 bolinhas, sem reposição.
A probabilidade de que as 3 bolinhas retiradas sejam
as mais leves é de:
1
a)
.
120
3
b)
.
10
3
c)
.
5
1
d)
.
30
3
e)
.
50
06. (Fuvest) De um baralho de 28 cartas, sete de cada
naipe, Luís recebe cinco cartas: duas de ouros, uma de
espadas, uma de copas e uma de paus. Ele mantém
consigo as duas cartas de ouros e troca as demais por
três cartas escolhidas ao acaso dentre as 23 cartas
que tinham ficado no baralho. A probabilidade de, ao
final, Luís conseguir cinco cartas de ouros é:
1
a)
.
130
1
b)
.
420
10
c)
.
1 771
25
d)
.
7 117
52
e)
.
8 117
a)
b)
c)
d)
e)
Número de
Internações
80
49
43
42
35
26
24
11
77
13
Considere que hipertensão arterial, doenças renais, doenças cardíacas e osteoporose estão associadas ao consumo excessivo de sódio e que as
fraturas de fêmur e ossos dos membros são causadas pela osteoporose.
Assim, a probabilidade de um idoso internado, escolhido ao acaso, ter como diagnóstico principal
uma doença associada ao consumo excessivo de
sódio, de acordo com a tabela, é igual a:
0,430.
0,370.
0,365.
0,325.
0,230.
08. (UPE) Dentre os esportes oferecidos aos estudantes de uma escola com 3 000 alunos, temos o futebol como preferência, sendo praticado por 600
estudantes. 300 estudantes dessa mesma escola
praticam natação, e 100 praticam ambos os esportes. Selecionando-se um estudante praticante de
futebol para uma entrevista, qual a probabilidade
de ele também praticar natação?
1
a)
.
3
2
b)
.
3
4
c)
.
3
1
d)
.
6
5
e)
.
6
09. (UDESC) Em uma associação serão eleitos um
presidente, um tesoureiro e dois revisores. Cada
membro vota em um candidato para presidente,
um para tesoureiro e um para revisor. Supondo
que haja 4 candidatos para presidente, 3 para tesoureiro e 6 para revisor, então a probabilidade de
todos os candidatos de um eleitor qualquer, que
não anulou nem votou em branco, serem eleitos é
de:
Aprofundamento 3°Ano e Curso
Página
6
a)
b)
c)
d)
e)
1
.
36
1
.
360
1
.
180
1
.
90
1
.
72
10. (Fuvest) Francisco deve elaborar uma pesquisa sobre
dois artrópodes distintos. Eles serão selecionados, ao
acaso, da seguinte relação: aranha, besouro, barata,
lagosta, camarão, formiga, ácaro, caranguejo, abelha,
carrapato, escorpião e gafanhoto.
Qual é a probabilidade de que ambos os artrópodes
escolhidos para a pesquisa de Francisco não sejam insetos?
49
a)
.
144
14
b)
.
33
7
c)
.
22
5
d)
.
22
15
e)
.
144
01. (PUC-RJ) A quantidade de anagramas da palavra
CONCURSO é:
a) 2 520.
b) 5 040.
c) 10 080.
d) 20 160.
e) 40 320.
02. (UEG) Érika resolve passear com a cachorrinha
Kika e, antes de sair do apartamento, escolhe colocar uma roupa e uma coleira na cachorrinha. Se
Kika tem 7 roupas e 3 coleiras, todas distintas, de
quantas maneiras Érika pode escolher uma roupa
e uma coleira para passear com a Kika?
a) 10.
b) 21.
c) 35.
d) 42.
03. (Insper) Um dirigente sugeriu a criação de um
torneio de futebol chamado Copa dos Campeões,
disputado apenas pelos oito países que já foram
campeões mundiais: os três sul-americanos (Uruguai, Brasil e Argentina) e os cinco europeus (Itália, Alemanha, Inglaterra, França e Espanha). As
oito seleções seriam divididas em dois grupos de
quatro, sendo os jogos do grupo A disputados no
Rio de Janeiro e os do grupo B em São Paulo.
Considerando os integrantes de cada grupo e as
cidades onde serão realizados os jogos, o número
de maneiras diferentes de dividir as oito seleções
de modo que as três sul-americanas não fiquem
no mesmo grupo é:
a) 140.
b) 120.
c) 70.
d) 60.
e) 40.
04. (FGV) Uma senha de internet é constituída de seis
letras e quatro algarismos em que a ordem é levada em consideração. Eis uma senha possível:
(a; a; b; 7; 7; b; a; 7; a; 7)
a)
b)
c)
d)
GABARITO
01. A
02. A
03. C
04. C
05. A
06. C
07. A
08. D
09. A
10. C
e)
Quantas senhas diferentes podem ser formadas
com quatro letras " a", duas letras "b" e quatro algarismos iguais a 7?
10!.
2 520.
3 150.
6 300.
10!
.
4! 6!

Aprofundamento 3°Ano e Curso
Página
7
05. (UFRGS) Considere o padrão de construção representado pelos desenhos abaixo.
a)
b)
c)
d)
e)
Na etapa 1, há um único triângulo equilátero. Na etapa
2, é traçado um segmento a partir dos pontos médios
de dois lados do triângulo da etapa 1, formando dois
triângulos equiláteros. Na etapa 3, é traçado um segmento a partir dos pontos médios de dois lados do triângulo menor da etapa 2, formando três triângulos
equiláteros. Na etapa 4 e nas etapas seguintes, o
mesmo processo é repetido em cada um dos triângulos
menores da etapa anterior.
O número de trapézios na 6ª etapa de construção é:
14.
15.
16.
17.
18.
06. (UEPA) Com as cidades imobilizadas por congestionamentos, os governos locais tomam medidas para
evitar o colapso do sistema viário. Por exemplo, em
Pequim, na China, serão sorteadas mensalmente 20
mil novas licenças de emplacamento para os 900 mil
interessados. Para o sorteio, os 900 mil interessados
foram divididos em 20 mil grupos com o mesmo número de integrantes.
Texto adaptado da revista National Geographic Brasil, edição 159-A.
a)
b)
c)
d)
e)
Se num desses grupos estão presentes 3 membros de
uma mesma família, a probabilidade de essa família
adquirir uma licença para emplacamento:
É inferior a 3%.
Está compreendida entre 3% e 4%.
Está compreendida entre 4% e 5%.
Está compreendida entre 5% e 6%.
É superior a 6%.
07. (Enem) O psicólogo de uma empresa aplica um teste
para analisar a aptidão de um candidato a determinado
cargo. O teste consiste em uma série de perguntas cujas respostas devem ser verdadeiro ou falso e termina
quando o psicólogo fizer a décima pergunta ou quando
o candidato der a segunda resposta errada. Com base
em testes anteriores, o psicólogo sabe que a probabilidade de o candidato errar uma resposta é 0,20.
A probabilidade de o teste terminar na quinta pergunta
é:
a) 0,02048.
b) 0,08192.
c) 0,24000.
d) 0,40960.
e) 0,49152.
08. (UPF) Duas bolsas de estudo serão sorteadas entre 9
pessoas, sendo 7 mulheres e 2 homens. Considerando-se que uma pessoa desse grupo não pode ganhar
as duas bolsas, qual a probabilidade de duas mulheres
serem sorteadas?
7
a)
.
12
7
.
9
2
c)
.
7
1
d)
.
21
7
e)
.
36
b)
09. (Unicamp) Um caixa eletrônico de certo banco
dispõe apenas de cédulas de 20 e 50 reais. No caso de um saque de 400 reais, a probabilidade do
número de cédulas entregues ser ímpar é igual a:
1
a)
.
4
2
b)
.
5
2
c)
.
3
3
d)
.
5
10. (Fuvest) O gamão é um jogo de tabuleiro muito
antigo, para dois oponentes, que combina a sorte,
em lances de dados, com estratégia, no movimento das peças. Pelas regras adotadas, atualmente,
no Brasil, o número total de casas que as peças de
um jogador podem avançar, numa dada jogada, é
determinado pelo resultado do lançamento de dois
dados. Esse número é igual à soma dos valores
obtidos nos dois dados, se esses valores forem diferentes entre si; e é igual ao dobro da soma, se
os valores obtidos nos dois dados forem iguais.
Supondo que os dados não sejam viciados, a probabilidade de um jogador poder fazer suas peças
andarem pelo menos oito casas em uma jogada é:
1
a)
.
3
5
b)
.
12
17
c)
.
36
1
d)
.
2
19
e)
.
36
GABARITO
01. C
02. B
03. D
04. C
05. B
06. E
07. B
08. A
09. B
10. C
Aprofundamento 3°Ano e Curso
Página
8
05. (Unioeste) O valor da expressão
153 4 – 4 153 3 3  6 153 2 32 – 4 153 33  34
é igual a:
a) 153 (153 – 3)3  3 .







4
b) 147 .
01. (Espcex/Aman) O termo independente d x no desen10
a)
b)
c)
d)
e)

1 
volvimento de  x3 –

x2 

110.
210.
310.
410.
510.
é igual a:
c) 15 4 3 4 .

d) 153 4 .
e) 15 4 10 4 .

06. (UDESC) Seja x a solução real da equação
4x  2
x
1
2

de m  x –
02. (UFRGS) Considere a configuração dos números dispostos nas colunas e linhas abaixo.
3
. Localizando na reta real os valores
2
1
1
1

, n  3 x 
 e p  2x  , torna4
8
10 


a)
b)
c)
d)
e)
...
Coluna 7
Coluna 6
Coluna 5
Coluna 4
1
2
3
4
5
6
7
Coluna 3
1
1
1
1
1
1
1
1
Coluna 2
Coluna 1
Linha 0
Linha 1
Linha 2
Linha 3
Linha 4
Linha 5
Linha 6
Linha 7
...
Coluna 0
se correto afirmar que:
a) m e n são equidistantes de p.
c) n está situado entre m e p.
d) p está situado entre n e m.
1
3
6
10
20
35
e) m, n e p estão todos situados à direita de x.
1
4
10
20
35
1
5
15
35
07. (CFT-MG)
1
6
21
1
7
64x2  16x
1
O número localizado na linha 15 e na coluna 13 é:
15.
91.
105.
120.
455.
03. (ESC. Naval) O coeficiente de x 5 no desenvolvimento
7
a)
b)
c)
d)
e)
b) m está situado entre n e p.
2

de   x3  é:
x


30.
90.
120.
270.
560.
O
2
conjunto
2x – 2
solução
da
equação
é o conjunto:
a) S  {2} .
b) S  {4} .
c) S  {– 2; 2} .
d) S  {2; 4} .
08. (UEPB) Sendo
10 – x 0,00115
, o valor de x 2 é

0,2
2,3
igual a:
a) 25.
b) 4.
c) 9.
d) 1.
04. (FGV-SP) Desenvolvendo-se o binômio P( x )  ( x  1)5 ,
podemos dizer que a soma de seus coeficientes é:
a) 16.
b) 24.
c) 32.
d) 40.
e) 48.
e) 16.
2
09. (ESPM) Se ( 4 x )2  16 2x , o valor de x x é:

a) 27.
b) 4.
c)
1
.
4
d) 1.
e) –
1
.
27
Aprofundamento 3°Ano e Curso
Página
9
10. (Espcex-Aman) Um jogo pedagógico foi desenvolvido
com as seguintes regras:
— Os alunos iniciam a primeira rodada com 256 pontos.
— Faz-se uma pergunta a um aluno. Se acertar, ele
ganha a metade dos pontos que tem. Se errar, perde
metade dos pontos que tem.
— Ao final de 8 rodadas, cada aluno subtrai dos pontos
que tem os 256 iniciais, para ver se "lucrou" ou "ficou
devendo".
O desempenho de um aluno que, ao final dessas oito
rodadas, ficou devendo 13 pontos foi de:
a) 6 acertos e 2 erros.
b) 5 acertos e 3 erros.
c) 4 acertos e 4 erros.
d) 3 acertos e 5 erros.
e) 2 acertos e 6 erros.
01. (UERJ) Observe a matriz A, quadrada e de ordem
três.
 0,3 0,47 0,6 


A  0,47 0,6
x 
 0,6
x
0,77 
Considere que cada elemento aij dessa matriz é o
a)
b)
c)
d)
valor do logaritmo decimal de (i  j) . O valor de x é
igual a:
0,50.
0,70.
0,77.
0,87.
02. (UFSM) Quando um elemento radioativo, como o
Césio 137, entra em contato com o meio ambiente,
pode afetar o solo, os rios, as plantas e as pessoas. A radiação não torna o solo infértil, porém tudo
que nele crescer estará contaminado.
A expressão Q(t )  Q0 e– 0,023 t , representa a
quantidade, em gramas, de átomos radioativos de
Césio 137 presentes no instante t, em dias, onde
Q0 é a quantidade inicial.
O tempo, em dias, para que a quantidade de Césio
137 seja a metade da quantidade inicial é igual a:
(Use l n 2  0,69 ).
60.
30.
15.
5.
3.


a)
b)
c)
d)
e)
03. (PUC-RJ) Se log 0,5 x  – 3 , então
a)
b)
c)
d)
e)
3
x  x 2 vale:
3
.
4
6.
28.
50.
66.
04. (PUC-PR) O número de bactérias N em um meio
de cultura que cresce exponencialmente pode ser
determinado pela equação N  N0 ek t em que


N0 é a quantidade inicial, isto é, N0  N(0) e k é a
GABARITO
01. B
02. C
03. E
04. C
05. E
06. D
07. A
08. E
09. B
10. B
a)
b)
c)
d)
e)
constante de proporcionalidade. Se inicialmente
havia 5 000 bactérias na cultura e 8 000 bactérias 10 minutos depois, quanto tempo será necessário para que o número de bactérias se torne
duas vezes maior que o inicial? (Dados:
l n 2  0,69 e l n 5  1,61 ).
11 minutos e 25 segundos.
11 minutos e 15 segundos.
15 minutos.
25 minutos.
25 minutos e 30 segundos.
Aprofundamento 3°Ano e Curso
Página
10
05. (UFRGS) Atribuindo para log 2 o valor 0,3, então o
a)
b)
c)
d)
e)
valor de 100
3.
4.
8.
10.
33.
0,3
10. (Unicamp)
zi
2014
é:
O
módulo
1987
é igual a:
–i
do
número
complexo
a)
2.
b) 0 .
3.
c)
d) 1 .
06. (Unicamp) Sejam x e y números reais tais que
x  yi  3  4i , onde i é a unidade imaginária. O valor
de x y é igual a:
–2.
– 1.
1.
2.

a)
b)
c)
d)
07. (UEL) Leia o texto a seguir.
Na virada do século XVIII para o século XIX, um agrimensor norueguês, Wessel (1798), e um desconhecido
matemático suíço, Argand (1806), foram, aparentemente, os primeiros a compreender que os números complexos não têm nada de "irreal". São apenas os pontos
(ou vetores) do plano que se somam através da composição de translações e que se multiplicam através da
composição de rotações e dilatações (na nomenclatura
atual). Mas essas iniciativas não tiveram repercussão
enquanto não foram redescobertas e apadrinhadas,
quase simultaneamente, por Gauss, grande autoridade
daquele tempo que, já em vida, era reconhecido como
um dos maiores matemáticos de todos os tempos.
Adaptado de: CARNEIRO, J. P. “A Geometria e o Ensino dos Números
Complexos”. Revista do Professor de Matemática. 2004. v.55. p.18.
a)
b)
c)
d)
e)
Assinale a alternativa que apresenta, corretamente,
uma composição de rotação dos pontos P  ( – 3; 4) e
Q  (2; – 3) representados pelos números complexos
z  – 3  4i e w  2 – 3i .
18  17i .
– 6 – 12i .
– 1 i .
5  7i .
6  17i .
08. (UECE) Se x e y são números reais não nulos, pode-se
afirmar corretamente que o módulo do número complex – iy
xo z 
é igual a:
x  iy
a) 1 .
b) 2 .
c) x 2  y 2 .
d)
xy .
09. (UEPB) O produto dos números complexos
(3 – i)(x  2yi) é um número real quando o ponto
P  (x; y) está sobre a reta de equação:
a) 6x  y  0 .
b) 6x – y  0 .
c) x  6y  0 .
d) 6y – x  0 .
e) 3y – x  0 .
GABARITO
01. B
02. B
03. E
04. C
05. B
06. D
07. E
08. A
09. D
10. A
Aprofundamento 3°Ano e Curso
Página
11
01. (PUC-PR) Se
3
a)
b)
c)
d)
e)
(x – 2)
é um fator do polinômio
2
x  kx  12 x – 8 , então, o valor de k é igual a:
–3.
2.
3.
6.
–6.
08. (Unesp) Sabe-se que 1 é uma raiz de multiplicida-
02. (UECE) Se a expressão algébrica x 2  9 se escreve
a)
b)
c)
d)
identicamente como a( x  1)2  b( x  1)  c onde a, b e
c são números reais, então o valor de a – b  c é:
9.
10.
12.
13.
03. (Espcex/Aman) O polinômio
f ( x )  x 5 – x 3  x 2  1 , quando dividido por
a)
b)
c)
d)
e)
q( x )  x 3 – 3x  2 deixa resto r(x).
Sabendo disso, o valor numérico de r( – 1) é:
– 10 .
–4.
0.
4.
10 .
04. (ESPM) O trinômio x 2  ax  b é divisível por x  2 e
por x – 1 . O valor de a – b é:
a) 0.
b) 1.
c) 2.
d) 3.
e) 4.
05. (UFRGS)
a)
b)
c)
d)
e)
Considere
os
polinômios
p( x )  x 3
07. (UFRGS) Considere o polinômio
p( x )  x 4  2x 3 – 7x 2 – 8x  12 .
Se p(2)  0 e p(– 2)  0 , então as raízes do polinômio p(x) são:
a) – 2; 0;1 e 2 .
b) – 2; – 1; 2 e 3 .
c) – 2; – 1;1 e 2 .
d) – 2; – 1; 0 e 2 .
e) – 3; – 2;1 e 2 .
e
de 3 da equação x5 – 3x 4  4x 3 – 4x 2  3x – 1  0 .
As outras raízes dessa equação, no Conjunto Numérico dos Complexos, são:
a) (–1– i) e (1 i) .
b)
c)
d)
e)
(1 – i)2 .
(– i) e ( i) .
(– 1) e ( 1) .
(1 – i) e (1 i) .
09. (PUCRS) Algumas das raízes do polinômio, com
coeficientes reais e não nulos,
p( x )  ax 5  bx 4  cx3  dx 2  ex ,
em C, são: 2  3i, – 1 7i e ______:
a) – i .
b) – 1 – 7i .
c) – 2  3i .
d) – 3i .
e) – 7i .
10. (Insper) A equação x3 – 3x 2  7x – 5  0 possui
uma raiz real r e duas raízes complexas e não reais z1 e z 2 . O módulo do número complexo z1 é
igual a:
a)
2.
b)
5.
c) 2 2 .
d)
10 .
e)
13 .
q( x )  x 2  x . O número de soluções da equação
p(x)  q(x) , no conjunto dos números reais, é:
0.
1.
2.
3.
4.
06. (Unicamp) Considere o polinômio
p( x )  x 3 – x 2  ax – a , onde a é um número real. Se
x  1 é a única raiz real de p(x), então podemos afirmar
que:
a) a  0 .
b) a  1 .
c) a  0 .
d) a  1 .
GABARITO
01. E
02. D
03. A
04. D
05. D
06. C
07. E
08. C
09. B
10. B
Aprofundamento 3°Ano e Curso
Página
12