exp03MLC21 02 2006 - Ivan H. Bechtold

EXPERIÊNCIA 03
MEDIDAS DE RESISTÊNCIAS COM A PONTE DE WHEATSTONE
1. OBJETIVOS
a) Medir as resistências de resistores e de associações de resistores.
b) Estabelecer experimentalmente a relação entre a resistência de fios metálicos com seu comprimento e com
sua área de seção reta.
c) Calcular a resistência por unidade de comprimento e a resistividade de um fio de nicromo.
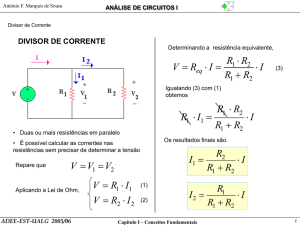
2. TEORIA BÁSICA
A Ponte de Wheatstone é um circuito muito utilizado em medidas elétricas, para obter o valor de
uma resistência desconhecida, a partir de um conjunto de outras já conhecidas e tomadas como padrão
(figura 1). Geralmente duas resistências são fixas, uma é ajustável e a quarta é a incógnita que se pretende
determinar. Com este propósito, entre A e B se estabelece a alimentação da fonte de tensão, e entre C e D é
conectado um galvanômetro como um indicador de corrente.
A resistência Rp é ligada em série com a fonte de tensão para limitar a corrente total da associação
e não faz parte da ponte.
Quando houver uma diferença de potencial entre os pontos C e D, o galvanômetro acusará a
passagem de corrente. Essa diferença de potencial poderá ser anulada através de um ajuste conveniente do
valor da resistência ajustável. Quando esta situação for obtida, tem-se VC = VD e, consequentemente, a
diferença de potencial entre os pontos A e C deve ser a mesma que entre A e D, e então
i1 R1 = i3 R3
(1)
i2 R2 = i4 R4
(2)
e, de maneira idêntica:
R1
R2
C
i1
i2
G
A
B
i4
i3
i
D
R3
R4
Rp
+
-
Figura 1 - Circuito elétrico da Ponte de Wheatstone
medidas de resistências com a ponte de Wheatstone – pág. 1
Dividindo a equação (1) pela equação (2), tem-se:
i1R1 i3R3
=
i2 R2 i4 R4
(3)
Como não passa corrente pelo galvanômetro, situação denominada de equilíbrio da ponte, i1 = i2 e
i3 = i4, resultando
R1 R3
=
R2 R4
(4)
Uma maneira prática de memorizar a condição de equilíbrio de uma ponte de Wheatstone é
observar que os produtos das resistências de resistores alternados são iguais: R1 x R4 = R2 x R3.
Se R1 for uma resistência desconhecida, agora denominada RX, e R2 uma resistência padrão
(standard) RS, então basta variar R3 e/ou R4 até equilibrar a ponte e obter
Rx = R S
R3
R4
(5)
Há duas formas comuns de pontes de Wheatstone: 1. - de caixas de resistências e
2. - de fio
deslizante. A ponte de caixa de resistências é uma forma compacta arranjada de tal maneira que a razão R3 / R4
possa ser variada em etapas decimais, por exemplo, de 0,001 até 1000 através da rotação de um dial. A
resistência padrão RS está incluída na caixa e pode ser variada de 1 a 9999 Ω. Nestas condições, o alcance
teórico de medidas de resistências está compreendido entre 0,001 e 9.999.000 Ω.
No nosso caso, a Ponte de Wheatstone utilizada é a de fio deslizante,constituída de um fio metálico
estendido sobre uma escala uniformemente dividida entre os pontos A e B e o contato pode ser feito em
qualquer ponto D por meio de um cursor deslizante, que se move ao longo do fio AB, conforme o esquema da
experiência, mostrado no item 4. A resistência padrão Rs é um conjunto de resistências em série cujos valores
variam de 1Ω a 1.111.110 Ω . As resistências R3 e R4 são substituídas por um fio metálico de raio uniforme “r”
e comprimentos parcelados em “a” e “ b”. Considerando que, se um dado resistor tiver o formato de um
cilindro uniforme de comprimento L e área de seção reta A, sua resistência pode ser calculada por:
R=ρ
l
A
(6)
onde ρ é a resistividade, que é uma propriedade específica de cada material. As resistências R3 e R4 serão
dadas por:
R3 = ρ
a
πr 2
e
R4 = ρ
b
πr 2
que, substituídas na equação (5) fornecem
RX = RS
a
b
(7)
medidas de resistências com a ponte de Wheatstone – pág. 2
A Tabela 1 fornece a resistividade ρ de alguns materiais a 20 oC.
Tabela 1 - Resistividade de alguns materiais a 20 oC ( x 10-8 Ω.m )
prata
1,6
cobre
1,7
aço
18,0
nicromo ( kanthal )
143,0
3. REFERÊNCIAS BIBLIOGRÁFICAS
1. D. Halliday,R.Resnick e J.Walker; Fundamentos de Física; Vol.3; Ed. LTC
2. Sears; Zemansky;Young e R.Fredman; Física III; Ed. Pearson,Addison Wesley.
3. P A.Tipler; Física-Eletricidade e Magnetismo,Ótica; Vol.2;4°Edição;Ed.LTC
4. Introdução ao Laboratório de Física; J.J.Piacentini, B.C.S.Grandi, M.P.Hofmann, F.R.R.de Lima,
E. Zimmermann; Ed. da UFSC.
4. ESQUEMA
+
Fonte de tensão
i
RX
Rp
RS
G
A
0
a
b
D
B
50
medidas de resistências com a ponte de Wheatstone – pág. 3
5. PROCEDIMENTO EXPERIMENTAL
PRIMEIRA PARTE - Resistências e associações
1. Monte o circuito conforme o esquema, colocando como resistência RX o resistor número 1. Antes de ligar a
fonte de tensão, verifique se os dois reguladores de tensão estão em seus valores mínimos, girados à esquerda.
Arbitre um valor inicial para a resistência RS na ordem de centenas de ohms. No decorrer das medidas este
valor poderá ser modificado. Chame o professor para verificar as conexões elétricas.
2. Ligue a fonte de tensão que aplicará automaticamente um valor pequeno de tensão. Observe que o ponteiro
do galvanômetro saiu de sua posição de equilíbrio. Desloque o cursor do potenciômetro de fio de modo a
restaurar o equilíbrio da ponte. O ponteiro deve retornar à posição zero. Os valores de a / b estão marcados na
escala superior da régua. Se o cursor ocupar posição acima do valor 2,0 ou abaixo do valor 0,5 para a/b, você
deverá procurar outro valor para RS e tentar novo equilíbrio.
3. Uma vez encontrado o ponto de equilíbrio da ponte, você pode aumentar a tensão da fonte até seu valor
máximo ( na ordem de 30 V ), e fazer o ajuste fino do cursor, de maneira que o galvanômetro acuse corrente
zero. Anote na Tabela I do relatório os valores de RS e a / b. Concluída a medida, antes de colocar outra
resistência para ser medida, você deve BAIXAR A TENSÃO DA FONTE AO MÍNIMO.
4. Meça as resistências dos resistores 2 e 3.
5. Meça as resistências das associações dos resistores 2 e 3, primeiro em série, depois em paralelo.
SEGUNDA PARTE - Resistência por unidade de comprimento
1. Meça as resistências dos fios de nicromo ( liga de níquel e cromo ) estendidos e de comprimento L, 2L, 3L,
4L e 5L utilizando o mesmo procedimento anterior. Meça o comprimento L do primeiro fio com uma régua
milimetrada. Os demais valores são múltiplos deste comprimento inicial. Anote na tabela II.
TERCEIRA PARTE - Resistividade
1. Meça as resistências dos fios de nicromo com áreas de seção reta de A, 2A, 3A, 4A e 5A seguindo o mesmo
procedimento . O diâmetro do fio de área A é 0,226 mm. Calcule a área A. As demais são múltiplas da área
inicial. Anote na tabela III.
medidas de resistências com a ponte de Wheatstone – pág. 4
6. RELAÇÃO DO MATERIAL
01 fonte de tensão/corrente(VCC), variáveis, 0 - 30 V /0-3A.
01 caixa de resistências padrão .
01 galvanômetro.
01 potenciômetro de fio deslizante.
01 tábua com 5 fios de nicromo em série.
01 tábua com 6 fios de nicromo em paralelo.
01 resistor de proteção.
01 resistor de 200 Ω (número 1).
01 resistor de 56 Ω - 10 % - 10 W , metálico (número 2).
01 resistor de 150 Ω - 10 % - 10 W , metálico (número 3)
10 cabos para conexões elétricas.
01 régua milimetrada.
7. QUESTIONÁRIO
1.a. Calcule o erro percentual entre os valores medidos da resistência dos três resistores e seus valores
nominais (Tabela I).
1.b. Calcule o erro percentual entre os valores medidos para as associações série e paralelo e seus valores
nominais calculados.
2. Faça o gráfico de RX em função do comprimento com os dados da tabela II. Calcule o coeficiente angular e
obtenha o valor da resistência por unidade de comprimento do fio de nicromo.
3. Faça o gráfico de RX em função de 1 / Área (tabela III) . Calcule o coeficiente angular. Calcule a
resistividade deste material e determine o erro percentual em relação ao valor tabelado.
4.a. Admitindo-se que a ponte esteja equilibrada com o cursor em a = 1 mm e com a menor resistência padrão
disponível no equipamento, calcule o valor da menor resistência que poderá ser medida com este.
4.b. Se a ponte estiver equilibrada com a = 499 mm e com a máxima resistência padrão disponível no
equipamento, calcule o valor da maior resistência que poderá ser medida com o mesmo.
5. Admitindo-se uma imprecisão de 0,5 mm na leitura da escala milimetrada do cursor deslizante, qual é o erro
esperado na medida de uma resistência de 100 Ω, caso o cursor esteja equilibrado em a = 250,0 mm? Este erro
depende da posição do cursor na régua milimetrada? Justifique sua resposta.
medidas de resistências com a ponte de Wheatstone – pág. 5
GRUPO:
,
TURMA:
. ALUNOS:
EXPERIÊNCIA 03
MEDIDAS DE RESISTÊNCIAS COM A PONTE DE WHEATSTONE
PRIMEIRA PARTE - Resistências e associações
Tabela I
Resistores
RS ( Ω )
RX ( Ω )
a/b
Rnom ( Ω )
erro %
1
2
3
série 2 e 3
paralelo 2 e 3
SEGUNDA PARTE - Resistência por unidade de comprimento
Tabela II
Resistores
comprimento ( m )
RS ( Ω )
RX ( Ω )
a/b
1L
2L
3L
4L
5L
6L
TERCEIRA PARTE - Resistividade
Tabela III
Resistores
Área
( 10 -8 m2 )
1 / Área
( 107 m-2 )
RS ( Ω )
a/b
RX ( Ω )
1A
2A
3A
4A
5A
medidas de resistências com a ponte de Wheatstone – pág. 6