A.4 Harmônicas Espaciais e Fatores de Enrolamento

Fundamentado no Livro: Principles of Eletric Power and Machines
Autor: P.C. Sen
TEORIA DOS ENROLAMENTOS TRIFÁSICOS DE MÁQUINAS SÍNCRONAS e ASSÍNCRONAS
O layout do enrolamento da máquina elétrica afeta a distribuição da Força Magneto-Motriz e o
seu desempenho. Todas as bobinas de um enrolamento podem ser colocadas em duas ranhuras ou
canais, esse tipo de enrolamento é conhecido como enrolamento concentrado. O enrolamento
concentrado requer grande espaço nos ranhuras e também, uma grande porção do estator ou rotor não
é utilizado. Excetuando-se as máquinas de menores potências, o enrolamento concentrado é muito
pouco usado. Nas máquinas de maiores potências as bobinas do enrolamento são geralmente
distribuídas ao longo de algumas ranhuras, e este enrolamento é denominado enrolamento distribuído.
Os enrolamentos distribuídos utilizam melhor a estrutura do estator, ou rotor, reduzindo também o
conteúdo de harmônicos nas tensões geradas. Neste apêndice serão discutidos as propriedades e os
efeitos dos diversos tipos de enrolamentos.
Notas: Os enrolamentos distribuídos reduzem as respectivas reatâncias, reduzem a amplitude
das harmônicas de campo magnético e melhoram a dissipação térmica devido as perdas por efeito
Joule.
A.1 Distribuição FMM
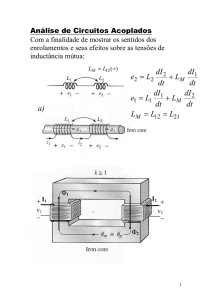
Considerando um enrolamento com N espiras colocadas em dois polos do estator de uma
máquina, como mostra a FIG. A.1.a. Se a corrente i fluir no enrolamento, a Fmm é definida pelo ângulo
Ѳ, e determinada pelo número de espiras pela expressão:
(A.1)
A distribuição da Força Magneto-motriz no espaço do entreferro é mostrado na Fig. A.1b.
Considerando que o espaço de ar é uniforme de comprimento g e a relutância magnética dos núcleos
do estator e do rotor desprezíveis, a distribuição de densidade do fluxo no espaço de ar é similar a
distribuição de FMM e determinada pela expressão:
(A.2)
A distribuição da densidade do fluxo da forma de onda quadrada, isto é, não senoidal, é
constituída pela soma das ondas senoidais da fundamental e de seus componentes harmônicos de
densidade de fluxo, ou seja:
1
(A.3)
(A.4)
Por se tratar de uma onda simétrica em relação ao eixo x, todas as harmônicas ímpares estão
presentes e os harmônicos pares são nulos. Na Fig. A.1c é mostrada as formas de onda da fundamental,
terceira harmônica e quinta harmônica. Cada uma das componentes das densidades de fluxos
harmônicos também induzem tensões harmônicas no enrolamento.
Fig A.1 Enrolamento concentrado. (a) Enrolamento de 2 pólos do estator. (b) Distribuição FMM
no espaço de ar. (c) Distribuição da densidade de fluxo no espaço de ar.
2
O conteúdo das harmônicas é reduzido se o enrolamento é distribuído em muitas ranhuras. Na
Fig. A.2a, é mostrado um enrolamento distribuído em 12 ranhuras. A distribuição FMM resultante do
enrolamento distribuído é mostrada na Fig A.2b. A componente fundamental é mostrada também nesta
figura. Constata-se que esta distribuição está mais próxima de ser senoidal pois é o resultado da
distribuição de um enrolamento com muitas ranhuras.
Para uma máquina ideal o enrolamento poderia ser constituído por uma infinidade de ranhuras
ou mesmo de condutores nas ranhuras e distribuídos senoidalmente (em vez de colocar o mesmo
número de condutores em cada ranhura) e a distribuição da FMM no espaço de ar seria senoidal. Essa
máquina ideal é impossível de ser construída. No entanto, é conveniente construir todas as bobinas
idênticas e colocá-los nas ranhuras. A Fig. A.3a mostra três bobinas idênticas. A distribuição FMM no
entreferro contém alguns componentes harmônicos, principalmente os de menor ordem. A figura A.3b
mostra o enrolamento do estator de uma máquina elétrica trifásica. Em uma máquina elétrica usual, o
enrolamento distribuído é distribuído em número de ranhuras finitas e com todas as bobinas idênticas.
Fig. A.2 –
3
Enrolamento Distribuído
Figura A.3 Bobina e enrolamento de uma máquina elétrica polifásica. (a) Bobinas. (b) Enrolamento de
um estator polifásico.
A.2 Tensões Induzidas
Para um enrolamento concentrado com N espiras por fase, a tensão rms induzida em cada fase
é determinada por:
E  4,44 * f * N * 
f = frequência
Ø = fluxo fundamental por polo.
Entretanto, se o enrolamento é distribuído em muitas ranhuras, a tensão induzida é determinada por:
E  4,44 * f * N *  * Ke
Ke é o fator de enrolamento.
Observe que este valor é menor que 1 e depende do tipo do
enrolamento.
4
5
A.3 Montagem do Enrolamento
Figura A.4a mostra um exemplo do enrolamento distribuído de 2 polos, trifásico, dupla camada
no estator. O enrolamento de dupla camada é utilizado principalmente em máquinas de grandes
potências. Nas máquinas de pequena potência, por uma questão de praticidade, utilizam-se
enrolamentos de camada única, ou simples que possuem a vantagem de conexões mais simplificadas no
e são mais econômicos para a fabricação. Os lados de bobinas da mesma fase são alocadas em ranhuras
adjacentes e denominadas de a1, a2, a3 e a4, constituindo o ângulo de fase sob um determinado polo.
Analogamente os lados de bobina alocados no polo oposto são denominados respectivamente por -a1, a2, -a3 e -a4 Em uma máquina trifásica o ângulo de fase é sempre 60º. Em um enrolamento de dupla
camada, um lado da bobina, como a 1, é colocado no meio do enrolamento e o outro lado de -a1 é
colocado no início da ranhura. A figura A.4a mostra-se um passo de bobina pleno ou 180 graus elétricos,
ou seja, o lado de bobina a1 está deslocado de 180 graus elétricos do lado de bobina -a1.
Figura A.4b mostra um enrolamento distribuído em que as bobinas são menores que um passo
pleno. Este enrolamento é chamado de passo encurtado ou passo fracionado. A figura A.4b mostra uma
bobina com deslocamento entre os lados a1 e -a1 de 5/6 do passo pleno, ou seja, 150º elétricos.
Enrolamentos de passo encurtado são geralmente usados em máquinas polifásicas A.C., pois
reduzem o comprimento das cabeças de bobinas e reduzem significantemente, a amplitude de
determinadas harmônicas da distribuição da FMM, e, portanto da tensão induzida no enrolamento.
FIGURA A.4 – Enrolamento de Dupla Camada (estator).
A.3.1 Fatores de Enrolamento
A distribuição e a amplitude do passo das bobinas afetam a tensão induzida. Dois fatores serão
discutidos: (a) Fator de Distribuição Kd e (b) Fator de Passo Kp.
Fator de Distribuição Kd
Se todas as bobinas das fases dos enrolamentos estão localizadas em apenas duas ranhuras
(por exemplo, um enrolamento concentrado), as tensões induzidas na bobina estão na fase e por isso a
tensão do enrolamento é a soma aritmética da tensão individual nas bobinas. Caso, entretanto, as
bobinas estão distribuídas por várias ranhuras no espaço (enrolamento distribuído), as tensões induzida
6
nas bobinas não estão em fase, mas deslocadas uma da outra pelo ângulo  . A tensão no
enrolamento é a soma fasorial das tensões das bobinas. O fator de distribuição Kd é definido por:
 somafasori aldastensõesdasbobinas 
Kd  

 somaaritméticadastensõedasbobinas 
(A.7)
Onde:

= ângulo entre duas ranhuras adjacentes
q = número de ranhuras por polo e por fase,
ENROLAMENTO DISTRIBUIDO
Figura A.5 Tensão das bobinas em um enrolamento distribuído
7
O fator de distribuição pode ser determinado por um diagrama fasorial construído pela a
tensão das bobinas. Figura A.5 mostra um exemplo de q= 3. A tensão da bobina é definida pelos fasores
de módulos constantes RS, ST, e TU, cada qual é uma corda de um círculo com centro em 0 e
subentendido um ângulo  em 0. O fasor RU representa a resultante da soma das tensões RS, ST, e TU
do enrolamento. Da equação A.7 e Fig A.5,
 RU 
Kd  

 q(RS ) 
 2 Rx 
Kd  

 q(2 Ry ) 
 OR.sen(n / 2) 
Kd  

 qOR.sen( / 2) 
 Rx 
Kd  

 q(Ry ) 
 sen(n / 2) 
Kd  

 qsen( / 2) 
(A.8)
Fator de Passo Kp
ENROLAMENTO TRIFÁSICO – PASSO INTEIRO OU PASSO PLENO
8
ENROLAMENTO TRIFÁSICO – PASSO ENCURTADO OU PASSO CURTO
ENROLAMENTO TRIFÁSICO – A PASSO INTEIRO B PASSO ENCURTADO
9
Para o enrolamento de passo encurtado, onde o passo da bobina é menor que um passo polar,
ou seja, menor que 180º elétricos, a tensão induzida é menor que a tensão que poderia ser induzida no
passo pleno da bobina. O fator de passo é definido como:
 tensaoinduzidanabobi nadecurtopasso 
Kd  

 tensaoinduzidanabobi nadepolocheio 
(A.9)
Figura A.6 mostra a tensão induzida em uma bobina de passo-completo e uma bobina de passo
encurtado. O passo da bobina para a bobina de encurtado é [180º - ϒº]; que é, encurtada em relação a
uma bobina de passo completo pelo ângulo de ϒº. A tensão da bobina é:
et  e1  e2
(A.10)
Figura A.6 Tensão das bobinas em passo completo e bobinas de encurtado
Para a bobina de passo pleno as tensões e1 e e2 são iguais no mesmo instante. Entretanto, para
a bobina de passo curto, quando e1 é máxima, e2 não é máxima. Esse fenômeno pode ser representado
no diagrama fasorial destas tensões, como mostra a Fig. A.6b. Para a bobina de encurtado, o fasor E2
para a tensão e2 é fase-deslocada pelo ângulo ϒº do fasor E1 para a tensão e1. Da Eq. A.9 e Fig. A.6b e
assumindo E1=E2=Er.
 2 E cos y / 2 
Kp  

2E


Kp  cos y / 2
(A.11)
Fator de Enrolamento Ke
Caso as bobinas de um enrolamento estão distribuídas em várias ranhuras e as bobinas são de
encurtado, a tensão induzida no enrolamento será afetada por ambos os fatores
enrolamento Ke para tal enrolamento é:
Ke  Kp  Kd
Kd e Kp. O fator de
(A.12)
10
Exemplo A.1
O estator de uma máquina trifásica possui 9 ranhuras por polo e o enrolamento de camada
dupla. As bobinas possuem passo encurtado de 7/9. Determine o fator de enrolamento.
Solução
180 º 
Ângulo da ranhura   
  20 º
 9 
7
Bobina encurtada=    180 º  140 º
9
A bobina possui passo encurtado de
Número de ranhura por polo
  180º 140º  40º
9 
q 3
3
Da Eq. A.8
 sen(3  20 º / 2) 
Kd  
  0,9598
 3 sen(20 º / 2) 
Da Eq. A.12
Ke  0,9598  0,9397  0,9019
Da Eq. A.11
 cos(40 º ) 
Kp  
 0,9397
2


Devido a da distribuição e encurtamento a tensão do enrolamento é reduzida para um fator de 0,9019
11
A.4 Harmônicas Espaciais e Fatores de Enrolamento
Nas Equações A.5 e A.6 são assumidas que a tensão induzida é senoidal. Entretanto, se a
distribuição de densidade de fluxo não é senoidal, a tensão induzida também não será senoidal. O fator
de distribuição, o fator de passo, e fator de enrolamento será diferente para cada tensão harmônica.
A diferença de fase entre as tensões harmônicas de ordem h de bobinas adjacentes é
h*  .
Por isso, o fator de distribuição para a ordem h harmônica é determinada por:
 sen(qh / 2) 
Kdh  

 qsen(h / 2) 
(A.13)
O efeito de distribuir o enrolamento ao longo de várias ranhuras é ilustrado na Tabela A.1. Para
valores de q (por exemplo, número de ranhuras por pólo por fase) variando de 1 para 6 (q=1 representa
um enrolamento concentrado), O fator de distribuição da fundamental varia de 1 para 0,9561. Deste
modo, a tensão fundamental será reduzida se o enrolamento é distribuído ao longo de várias ranhuras.
Entretanto, a Tabela A.1 mostra que distribuindo o enrolamento resultará na redução significativa no
conteúdo harmônico da tensão induzida no enrolamento.
Na bobina de encurtado a diferença de fase entre as tensões harmônicas de ordem h de
bobinas de dois lados é h*  . Por isso, o fator de passo para a ordem h harmônica é
Kph  cos( h / 2)
(A.14)
Tabela A.1 Fator de Distribuição na Máquina Trifásica
Fator de Distribuição para Harmônicos
q
h=1
3
5
7
9
11
1
1.000
1.000
1.000
1.000
1.000
1.000
2
0,966
0,707
0,259
0,259
0,707
0,966
3
0,960
0,667
0,218
0,177
0,333
0,177
4
0,958
0,653
0,205
0,158
0,271
0,126
5
0,957
0,647
0,200
0,149
0,247
0,110
6
0,956
0,644
0,197
0,145
0,236
0,102
infinito
0,955
0,637
0,191
0,136
0,212
0,087
q = 1, enrolamento concentrado; q > 1, enrolamento distribuído.
A variação dos fatores de passo harmônicos para diferentes valores do passo da bobina é
mostrada na Tabela A.2. A tensão harmônica diminui no passo encurtado da bobina, melhorando a
forma de onda da tensão induzida no enrolamento. É possível impor que certa harmônica seja
12
completamente eliminada da tensão de enrolamento, optando por um passo para a bobina que faça o
fator de passo zerar para aquela harmônica. Para eliminar a ordem h da tensão harmônica,
cos(h / 2)  0
Ou
 h 
   90 º
 2 
Ou
 180 º 


 h 
(A.15)
(A.16)
Deste modo, para eliminar a terceira harmônica, as bobinas devem possuir passo encurtado por:
  180 º / 3  60 º
Tabela A.2 Fator de Passo na Máquina Trifásica
Fator de Passo para Harmônicos
Bobina
(180º -

º)
h=1
3
5
7
9
11
120º ou 2/3
0,866
0,000
0,866
0,866
0,866
0,866
144º ou 4/5
0,951
0,588
0,000
0,588
0,951
0,951
150º ou 5/6
0,966
0,707
0,259
0,259
0,707
0,966
154º ou 6/7
0,975
0,782
0,434
0,000
0,434
0,782
160º ou 8/9
0,985
0,866
0,643
0,342
0,000
0,342
180º ou 1
1.000
1.000
1.000
1.000
1.000
1.000

= 0º para bobina de passo pleno
O fator de enrolamento correspondente para a ordem h da tensão harmônica é
Keh  Kdh  Kph
(A.17)
Onde Kdh e Kph são dadas pelas Equações A.13 e A.14, respectivamente.
13
A.5 Tensões Harmônicas no Tempo
A forma de onda da tensão induzida no enrolamento depende da distribuição no entreferro da
densidade de fluxo. Esta distribuição de densidade de fluxo não é puramente senoidal. Por exemplo, nas
máquinas síncronas o espaço de distribuição de densidade de fluxo do pólo do rotor não é senoidal. Nas
máquinas indutivas, motores assíncronos, o fluxo magnético no entreferro é produzido pelas correntes
do enrolamento e a distribuição de densidade de fluxo espacial também não é senoidal. A distribuição
das bobinas do enrolamento pode melhorar em muito a distribuição de densidade de fluxo espacial (Fig.
A.2) mas não torná-lo puramente senoidal.
Devido da distribuição de densidade de fluxo espacial não senoidal, a tensão induzida no
enrolamento irá conter harmônicos. Com a distribuição do enrolamento das bobinas, as tensões
harmônicas podem ser sensivelmente reduzidas. Certamente a fundamental também será reduzida,
embora, felizmente, por uma pequena quantia. Os fatores de enrolamento, discutido anteriormente,
representa a redução por unidade da fundamental e cada harmônica resultando da distribuição do
enrolamento das bobinas.
A Figura A.7 mostra uma típica distribuição espacial de densidade de fluxo, que pode ser expressa por:
B( )  B
sen( )  B
sen(3 )  B
sen(5 )  B
sen(7 )... (A.18)
1(max)
5(max)
7(max)
3(max)
Assim, a tensão induzida no tempo possui a expressão:
E ( wt )  E1(max) sen(wt )  E (max) sen(3wt )  E5(max) sen(5wt )  E 7(max) sen(7wt )...
3
14
Figura A.7 Distribuição espacial de densidade de fluxo
A fundamental e as densidades de fluxo da terceira harmônica são também mostradas. Se a
fundamental corresponde para uma máquina de “2p=pólo”, então a terceira harmônica pode ser
considerada para corresponder para uma máquina de “2*3p-pólo”. Cada componente da distribuição de
densidade de fluxo induzirá uma tensão no enrolamento.
Para um enrolamento concentrado de N espiras por fase, a tensão induzida rms em cada fase
pela componente fundamental da densidade de fluxo é
E1  4,44  f  N  1
(A.19)
Onde o subescrito 1 denota a fundamental, f a freqüência, e 1 o fluxo fundamental por pólo.
Devido um enrolamento distribuído em corda, a tensão fundamental é
E1  4,44  f  N  1  Ke1
(A.20)
onde Ke1  Kd1 Kp1 é o fator de enrolamento fundamental, o que é ligeiramente inferior a unidade
de uma máquina trifásica.
O espaço harmônico na onda de densidade de fluxo induz um tempo nas tensões harmônicas
no enrolamento. Para a ordem h do fluxo harmônico, a tensão induzida é
Eh  4,44  h  f  N   ph  K eh
onde
 ph é o fluxo por pólo correspondente para a ordem h harmônica da densidade de fluxo.
Seja D= diâmetro do entreferro
Então
(A.21)
L= comprimento do polo 2p= número de polos p = pares de polos
 ph  Ah  Bh
(A.22)
15
 * D* L 

Ah  
h
*
2
*
p


Ah na área de ordem h pólo harmônico,
Bh é a média densidade de fluxo para a ordem h harmônica,
(A.23)
 2B

Bh   h(max) 



(A.24)
Bh(max) é a amplitude da ordem h onda de densidade de fluxo harmônico.
Das Equações A.22, A.23, e A.24,
 DL  Bh(max) 


p
h



 ph  
(A.25)
B

 K  h(max) 
h


(A.26)
Das Equações A.21 e A.26,
Eh  K * B
h (max)
* Keh
(A.27)
4,44 * D * L * N * f
p
K
A tensão induzida total rms no enrolamento é
2
2
2
1/ 2
E  ( E 2  E  E  E  ...)
1
E(
3
(A.28)
1/ 2
Eh )
.
2
h  1,3,5...
7
5
(A.29)
É possível demonstrar que na máquina trifásica a tripla tensão harmônica (por exemplo,
terceira e múltiplos) não ocorre na tensão de linha. A tensão de linha portanto é mais senoidal que a
tensão de fase (por exemplo, enrolamento). A tensão de linha rms é
2
2
1/ 2
EL  3 ( E 2  E  E  E 2...)
1
7
5
11
(A.30)
16
RESUMO DA TEORIA DOS ENROLAMENTOS E HARMÔNICAS:
Eh  4,44  h  f  N   ph  K eh
ou
Eh  K * B
h (max)
K
* K eh
Tensão induzida para a harmônica h
4,44 * D * L * N * f
p
Constante da Máquina
q = Número de ranhuras / polo e fase
 sen(qh / 2) 
Kdh  

 qsen(h / 2) 
fator de distribuição para a harmônica h
Kph  cos(h / 2)
Keh  Kph  Kdh
fator de passo para a harmônica h
fator de enrolamento para a harmônica h
E  ( E12  E 32  E 52  E 72  ...)1 / 2
2
2
1/ 2
EL  3 ( E 2  E  E  E 2...)
1
7
5
11
tensão de fase
tensão de linha para ligação Y
17
Exemplo A.2
Um gerador síncrono possui um enrolamento de armadura de estator 3  , 60 Hz, oito polos, 96
ranhuras e está conectado estrela. O passo de bobina é de 9/12. A densidade de fluxo no entreferro
B (ϴ) apresenta conteúdo de terceira e de amplitudes respectivamente de 30% e 15% da fundamental.
Determine a razão entre a tensão de linha e tensão de fase.
 96 
q
  4 ranhuras /pólo fase
 83
Solução
 180 º 
  15 º
 3 4 
 
  315º  45º
Os fatores de distribuição são
 sen(4 15 º / 2) 
Kd1  
  0,9577
 4  sen(15 º / 2) 
 sen(4  3 15 º / 2) 
Kd 3  
  0,6533
 4  sen(3 15 º / 2) 
 sen(4  5 15 º / 2) 
Kd 5  
  0,2053
 4  sen(5 15 º / 2) 
Os fatores de passo são
Kp1  cos(45º / 2)  0,9239
Kp3  cos(3  45º / 2)  0,3827
Kp5  cos(5  45º / 2)  0,3827
Os fatores de enrolamento são
Ke1  Kd1 Kp1  0,9577  0,9239  0,8848
Ke3  Kd 3  Kp3  0,6533  0,3827  0,2500
Ke5  Kd 5  Kp5  0,2053  (0,3827 )  0,0786
Da Equação A.27, a tensão fundamental rms é
E1  KB1(max)Ke1
 K  1 0,8848  0,8848 K
18
A terceira e quinta tensões harmônicas são
E3  KB3(max)Ke3
 K  0,3  0,25  0,075 K
E5  KB (max)Ke5  K  0,15  0,0786  0,0118 K
5
A tensão de fase é
2
2
2
1/ 2
E  ( E 2  E  E  E  ...)
1
3
5
7
E  K (0,88482  0,0752  0,01182  ... )1/ 2
E  0,8881 K
A tensão de linha é
2
1/ 2
EL  3 ( E 2  E  ...)
ou EL 
1
5
2
1/ 2
EL  3 0,8848K
3 (0,88482  0,0118  ...)
A proporção da tensão de linha para a tensão de fase é
 EL   3  0,8848 
 3  0,9963


 E   0,8881 
Note que a tensão de linha é ligeiramente mais baixa
3 vezes a tensão de fase devido a
ausência de tensões de terceira harmônica na tensão de linha.
19
Problemas
A.1- Um gerador síncrono de 4 polos possui um enrolamento de armadura, 3  , ligação
estrela, com 36 ranhuras, camada dupla e passo de bobina de 140º e conectado-estrela. A distribuição
de densidade de fluxo no espaço é determinada pela expressão:
B( )  1,00 sen( )  0,4 sen(3 )  0,2 sen(5 )
. Determine em termos da tensão fundamental E1 rms.
a) Os valores rms da tensão de fase EF.
b) Os valores rms da tensão de linha EL.
A.2- Um gerador síncrono 3  , 60 Hz, 6 polos, conectado-Y possui um enrolamento de armadura de
camada-dupla com 108 ranhuras. O passo da bobina é 150º e cada bobina possui 30 espiras. O fluxo no
entreferro devido ao campo magnético dos polos contém componentes harmônicas de terceira e quinta
ordem nas magnitudes de 30 e 20%, respectivamente, relativa para a fundamental. O fluxo fundamental
por pólo é 0,01 webers.
a)
Determine os valores eficazes (rms) da tensão fundamental e das tensões harmônicas induzidas
no enrolamento do estator.
b) Determine o valor eficaz ( rms) da tensão de fase do estator.
c) Determine o valor eficaz ( rms) da tensão de linha do estator.
A.3- O enrolamento 3  , de um gerador síncrono de oito polos, 750rpm, conectado-Y possui as
seguintes características:
Total de ranhuras no estator = 96
Condutores em cada ranhura = 20
A configuração do enrolamento do estator é camada dupla e o passo é encurtado para eliminar a tensão
induzida de terceira harmônica O Fluxo fundamental por polo = 0,12 Wb
A análise do fluxo magnético no entreferro contem componentes de quinta e sétima harmônica de
amplitudes de 25 e 15%, respectivamente da fundamental. Assim, determinar:
a) O número de espiras por fase do enrolamento do estator.
b) O passo da bobina em graus elétricos e em número de ranhuras.
c) A frequência da tensão fundamental.
d) Os valores rms das tensões de fase e linha.
A.4- Um gerador síncrono, 3  , 60 Hz, oito polos possui 96 ranhuras no estator. O passo da bobina do
enrolamento é 135º. A tensão de fase (linha neutro) contém fundamental, terceira, e quinta harmônicas
nas amplitudes de 100, 25, e 5%, respectivamente. O valor medido rms da tensão de fase é 12KV.
a) Determine os valores rms de cada componente harmônicos de tensão na fase.
b) Determine o valor total rms da tensão de linha.
c) Determine as amplitudes de densidade de fluxo harmônico no entreferro em relação a densidade
de fluxo da fundamental.
20
As características dos geradores síncronos WEG são explicitadas abaixo. Explique o significado dos itens
referentes a tensões disponíveis, distorção harmônica total e passo encurtado.
21
22