topografiapoli

TOPOGRAFIA
AULA 11
ALTIMETRIA
1. Introdução
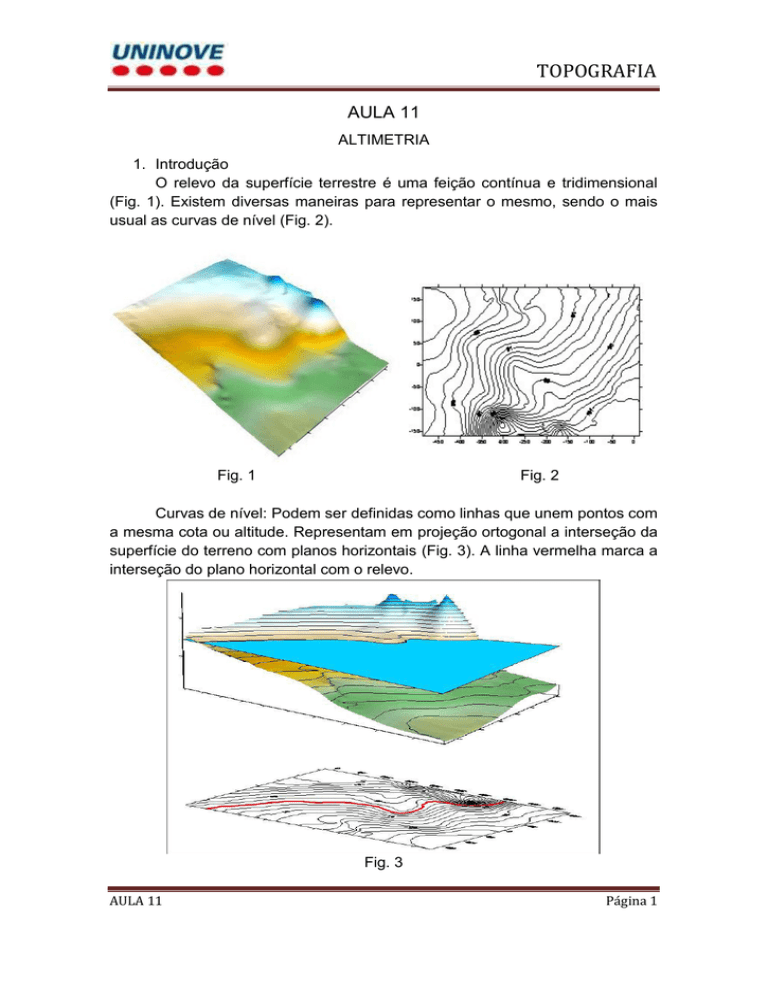
O relevo da superfície terrestre é uma feição contínua e tridimensional
(Fig. 1). Existem diversas maneiras para representar o mesmo, sendo o mais
usual as curvas de nível (Fig. 2).
Fig. 1
Fig. 2
Curvas de nível: Podem ser definidas como linhas que unem pontos com
a mesma cota ou altitude. Representam em projeção ortogonal a interseção da
superfície do terreno com planos horizontais (Fig. 3). A linha vermelha marca a
interseção do plano horizontal com o relevo.
Fig. 3
AULA 11
Página 1
TOPOGRAFIA
Perfis transversais: são cortes verticais do terreno ao longo de uma
determinada linha. Um perfil transversal (Fig. 4) é obtido a partir da interseção
de um plano vertical com o terreno (Fig. 5).
Fig. 4
Fig. 5
Durante a representação de um perfil, costuma-se empregar escalas
diferentes para os eixos X e Y, buscando enfatizar o desnível entre os pontos,
uma vez que a variação em Y (cota ou altitude) é menor. Por exemplo, pode-se
utilizar uma escala de 1:500 em X e 1:50 em Y.
As curvas de nível podem ser classificadas em curvas mestras ou
principais e secundárias. As mestras são representadas com traços diferentes
das demais (mais espessos, por exemplo), sendo todas numeradas. As curvas
secundárias complementam as informações (Fig. 6).
Fig. 6
AULA 11
Página 2
TOPOGRAFIA
Algumas regras básicas a serem observadas no traçado das curvas de
nível:
a) As curvas de nível são "lisas", ou seja, não apresentam cantos.
b) Duas curvas de nível nunca se cruzam.
c) Duas curvas de nível nunca se encontram e continuam em uma só
d) Quanto mais próximas entre si, mais inclinado é o terreno que
representam
AULA 11
Página 3
TOPOGRAFIA
2. Métodos para a interpolação e traçado das curvas de nível
Com o levantamento topográfico altimétrico são obtidos diversos pontos
com cotas conhecidas. A partir destes é que as curvas serão desenhadas (Fig.
7). Cabe salientar a necessidade das coordenadas planas dos pontos para
plotá-los sobre a carta. O número de pontos e sua posição no terreno
influenciarão no desenho final das curvas de nível.
Fig. 7
O que se faz na prática é, a partir de dois pontos com cotas conhecidas,
interpolar a posição referente a um ponto com cota igual a cota da curva de
nível que será representada (Fig. 8). A curva de nível será representada a partir
destes pontos.
Fig. 8
Utiliza-se uma regra de três para a interpolação das curvas de nível.
Devem ser conhecidas as cotas dos pontos, a distância entre eles e a
eqüidistância das curvas de nível. Tomando-se como exemplo os dados
apresentados na Fig. 9, sabe-se que a distância entre os pontos A e B no
AULA 11
Página 4
TOPOGRAFIA
desenho é de 7,5 cm e que o desnível entre eles é de 12,9m. Deseja-se
interpolar a posição por onde passaria a curva com cota 75m.
Fig. 9
É possível calcular o desnível entre o ponto A e a curva de nível com
cota 75m (75m - 73,2 = 1,8m). Sabendo-se que em 7,5 cm o desnível entre os
pontos é de 12,9 m, em "x" metros este desnível será de 1,8 m.
Neste caso, a curva de nível com cota 75m estará passando a 1,05cm
do ponto A. Da mesma forma, é possível calcular os valores para as curvas 80
e 85m (respectivamente 3,9 e 6,9cm). A Fig. 10 apresenta estes resultados.
Fig. 10
Adaptado de Fundamentos de Topografia – Veiga, Zanetti & Faggion
AULA 11
Página 5
TOPOGRAFIA
Exercício 1 – Calcule as cotas dos pontos 1 e 2.
751
752
1
753
2
Exercício 2 – Dadas as curvas de nível e os pontos A e B, pede-se para traçar
o perfil da estrada entre os pontos A e B.
AULA 11
Página 6
TOPOGRAFIA
Exercício 3 – Dados os pontos cotados, desenhar as curvas de nível. Desenhar
as curvas com eqüidistância de 1,0 m. As cotas estão em metros.
AULA 11
Página 7