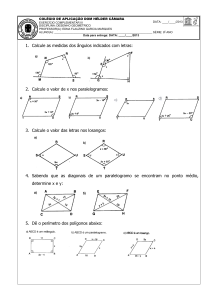
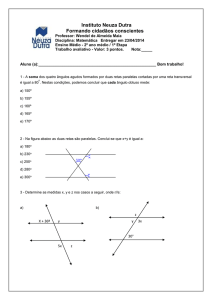
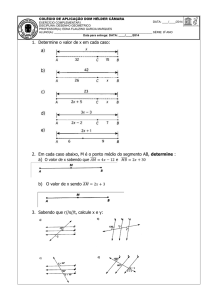
MATEMÁTICA II
2a LISTA DE REVISÃO
PROF. LUIZ PAULO
POLÍGONOS / QUADRILÁTEROS
01 – Se, em um polígono convexo, o número de diagonais é quatro vezes o número de lados, então, a soma de
seus ângulos internos, medida em retos, é
a)
b)
c)
d)
e)
9
11
12
16
18
02 – De um dos vértices de um polígono convexo podemos conduzir, no máximo, 9 diagonais. A soma de
seus ângulos internos, em graus, é
a)
b)
c)
d)
e)
720o
1 080o
1 440o
1 800o
2 160o
03 – O número de lados de dois polígonos convexos são números pares consecutivos e um deles possui 11
diagonais a mais que o outro. A soma do número de lados desse polígonos é
a)
b)
c)
d)
e)
12
14
16
18
20
04 – (PUC-MG) – Qual polígono regular possui ângulo interno de 108 o ?
a)
b)
c)
d)
e)
Pentágono
Hexágono
Heptágono
Octógono
Dodecágono
05 – (PUC) – O ângulo formado pelas bissetrizes internas de dois ângulos consecutivos de um polígono
regular de 20 lados, em graus, é
a)
b)
c)
d)
e)
80
72
36
20
18
06 – (FUVEST) – A, B, C e D são vértices consecutivos de um hexágono regular. A medida, em graus, de um
dos ângulos formados pelos diagonais AC e BD é
a)
b)
c)
d)
e)
90
100
110
120
150
07 – (FUVEST/SP) - Na figura, ABCDE é um pentágono regular. A medida, em graus, do ângulo é
a)
b)
c)
d)
e)
320
340
360
380
400
A
B
C
E
D
08 – As bissetrizes de dois vértices não opostos de um paralelogramo cortam-se formando um ângulo de
a)
b)
c)
d)
e)
30o
45o
60o
90o
120o
09 - (FUVEST) Dois ângulos internos de um polígono convexo medem 130º cada um e os demais ângulos
internos medem 128º cada um. O número de lados do polígono é:
a) 6
b) 7
c) 13
d) 16
10 – No paralelogramo ABCD da figura, AB̂C é o dobro de AM̂D e AM = MB. Se o perímetro de ABCD é
24 cm, então, o lado BC, em centímetros, é
a)
b)
c)
d)
e)
4 cm
5 cm
6 cm
8 cm
9 cm
11 – (UNESP) – Considere as seguintes preposições:
todo quadrado é um losango;
todo retângulo é um paralelogramo;
todo quadrado é um retângulo;
todo triângulo eqüilátero é isósceles.
Pode-se afirmar que
a)
b)
c)
d)
e)
só uma é verdadeira.
todas são verdadeiras.
só uma é falsa.
duas são verdadeiras.
todas são falsas.
12 – (UFMG) – Seja P o conjunto de todos os paralelogramos.
Seja R o conjunto de todos os retângulos.
Seja L o conjunto de todos os losangos.
Seja Q o conjunto de todos de quadrados.
Marque a alternativa errada.
a)
b)
c)
d)
e)
RP
LP
RL=Q
Q–R=
RL=P
13 – (FUVEST) – No retângulo a seguir, o valor em graus, de + é
a)
b)
c)
d)
e)
50
90
120
130
220
14 – (UFMG-adaptação) – O retângulo de lados a e b se decompõe em quatro quadrados, conforme figura.
a
Calcule .
b
a)
b)
5
3
2
3
c)
d)
4
5
2
5
15 – (UMC-SP) - Um tapete retangular de 136 cm de largura tem, na sua composição, retângulos e losangos,
conforme figura abaixo.
A
136
B
Os losangos têm seus vértices nos pontos médios dos lados do retângulo que os contém e os retângulos têm
seus vértices nos pontos médios dos lados do losango.
A medida do lado AB, em centímetros, é
a)
b)
c)
d)
e)
17
34
42
51
68
16 – (UFMG) – Num triângulo eqüilátero ABC, de 8 cm de lado, traça-se MN paralelo ao lado BC, de modo
que ele se decomponha num trapézio e num novo triângulo. O valor de MN para o qual o perímetro do
trapézio é igual ao do triângulo AMN é
a)
b)
c)
d)
3 cm
4 cm
5 cm
6 cm
17 – Observe a figura. Nela, ABCD é um retângulo e o triângulo CED é eqüilátero.
Se AB = 12 cm, então, o segmento EF, em centímetros, mede
a)
b)
c)
d)
2
3
4
5
18 – Num quadrilátero convexo ABCD, as diagonais AC e BC medem, respectivamente, 12 cm e 8 cm.
Unindo-se os pontos médios dos lados do quadrilátero ABCD, obtemos um novo quadrilátero cujo perímetro,
em centímetros, é
a)
b)
c)
d)
10
15
20
24
19 – Na figura, M e N são os pontos médios de AB e AC, respectivamente. Assinale a afirmativa falsa.
a)
b)
c)
d)
e)
MN // BC
AC + BC = 2 . CM
BC = 2 . MN
PC = 2 . PM
PB = 2 . PN
20 – Na figura abaixo, o ponto Q é médio de AB, e o segmento PQ é paralelo ao lado BC. Sendo AC = 30, a
medida do segmento PM é
a)
b)
c)
d)
e)
5
10
15
20
25
21 – Observe a figura. Nela,
AB = 3 cm, AC = 9 cm, BÂD = CÂD, BD̂A = 1 reto e M é ponto médio
de BC. O valor do segmento DM, em centímetros, é
a)
b)
c)
d)
e)
2
3
4
5
6
22 – Na figura, ABCD é um
graus, mede
paralelogramo, EF AD e AE = ED. Se BÂF = 40o , então, BĈD , em
a)
b)
c)
d)
100o
110o
120o
130o
23 – No trapézio isósceles da figura, DB é bissetriz de D̂ e é perpendicular a BC. O ângulo x mede
a)
b)
c)
d)
e)
30o
35o
40o
45o
50o
24 – (FUVEST) – No trapézio ARTP da figura, RB e AB estão contidos nas bissetrizes de R e A. Se B = 70 o ,
o valor de P + T é
a)
b)
c)
d)
e)
140o
130o
120o
110o
100o
25 – (UFMG) – O trapézio ABCD é isósceles, com AB // DC, AD = BC. A diagonal AC é perpendicular ao
lado BC. Os ângulos agudos do trapézio são a metade os seus ângulos obtusos. A base menor mede 2 cm. A
medida de AD, em cm, é
a)
b)
c)
d)
e)
1
2
3
4
5
26 – Na figura, M e P são, respectivamente, pontos médios de AB e MB. Se MN = 8, PQ mede
a)
b)
c)
d)
e)
10
12
16
18
24
27 – (FAAP) – No trapézio abaixo, o segmento MN que une os pontos médios M e N das diagonais e a base
AB têm ambos 7 cm de comprimento. Calcular o comprimento da base DC.
a)
b)
c)
d)
e)
7
10
12
21
14
28-Queremos desenhar no interior de um retângulo ABCD um losango AICJ, com o vértice I sobre o lado AB
e o vértice J sobre o lado CD. Sendo AB= 25cm e BC= 15cm,calcule o perímetro desse losango.
a)
b)
c)
d)
65cm
68cm
70cm
72cm
MATEMÁTICA I
2a LISTA DE REVISÃO
PROF. LUIZ PAULO
1) Duas torneiras A e B, com vazão constante, enchem um tanque em 6h, quando abertas simultaneamente.A
torneira A, sozinha, leva 5h a menos que a torneira B para encher o tanque. O tempo que a torneira B,
sozinha, gasta para encher o tanque, em horas, é:
a) 10
b) 12
c) 15
d) 2
2) Valéria saiu de casa com certa quantia.Gastou 3/7 na padaria e logo em seguida gastou 9/16 do que sobrou
na farmácia.Do que restou, Valéria ainda gasta 1/5 no armazém do Paulo.Se ela ainda volta para casa com
vinte e cinco reais e vinte centavos, calcule:
a) Qual a quantia que Valéria saiu de casa?
b) Quanto gastou na padaria?
c) Quanto gastou na farmácia?
d) E no armazém do Paulo?
3) Calculando o valor da expressão abaixo, encontramos para M o valor de:
M=
1 2 12
64 2
0,56
25 3
8 3 19
5
3
3
b)
5
2
c)
3
4
d)
3
a)
66
4) O valor exato do número P = 0,777... 0,2828...
7
a) 1
b) 10
c) 2
d) 20
5) Simplificando a expressão
2
3
, obtém-se:
3
2
1
é:
a)
5 6
5 6
6
13
c)
6
b)
d)
5
6
6) Uma fração é acrescida de seu quadrado, e o resultado desta soma, é uma outra fração que equivale a
82
27
da fração original. Podemos afirmar que
da fração original vale
27
5
a) 10
b) 11
c) 12
d) 13
7) Sabe-se que a média aritmética de 6 números inteiros, estritamente positivos, é 25. Qual é o maior valor
que um desses inteiros pode assumir?
a) 140
b) 143
c) 146
d) 150
8) O conjunto 5,6,
2
,0,15555..., 7 possui exatamente
5
a) 1 número natural, 1 número inteiro, 2 números racionais e 1 número real.
b) 1 número natural, 2 números inteiros, 4 números racionais e 5 números reais
c) 1 número natural, 1 número inteiro, 1 número racional e 2 números reais
d) 1 número natural, 2 números inteiros, 3 números racionais e 5 números reais
9) Encontre o valor de R, onde
R6
215 212
38 3 6
.
7
10
a) 4
b) 27
c) 31
d) 35
10) Uma empresa realiza um serviço em 6 horas enquanto outra empresa realiza o mesmo serviço em 4 horas.
Ao contratar as duas empresas para realizar esse serviço, um empresário deverá esperar que esse serviço seja
realizado em :
a) 120 minutos
b) 144 minutos
c) 154 minutos
d) 180 minutos
39 13 26 19 3 é igual a:
11) O valor exato da expressão
12
143 11
2
a) 1
b) 2
c) 3
d) 4
12) Na seqüência ao lado, 1,1,2,3,5,8,13,21,34,55,a,144,b,...conhecida como a sequência de fibonacci, qual é
o valor de a + b.?
a) 339
b) 336
c) 322
d) 330
3
13) O valor exato da expressão
64
8
4
3
1
16 1
é um número:
27 3
a) 4
b) 3
c) 2
d) 1
14) Os 50 primeiros colocados no vestibular da UFMG para o curso de Matemática, todos com pontuações
diferentes, foram colocados em duas salas, A e B. Na sala A ficaram os alunos com as 25 melhores notas e na
sala B os 25 alunos restantes. Ao trocarmos o último aluno da sala B com o primeiro da sala A, podemos
afirmar que:
a) A média da sala A aumentou.
b) A média da sala B diminuiu.
c) A média da sala A ficou menor que a da sala B.
d) A média da sala B aumentou.
a1 , a2 , a3 , a4 é igual a 12 e que a média aritmética dos
números a5 , a6 , a7 , a8 , a9 , a10 é igual a 17. Qual é a média aritmética dos números a1 ,......a10 ?
15) Sabe-se que a média aritmética dos números
a) 15
b) 14
c) 13
d) 16
16) Raíssa, Arthur e Teresa possuem juntos 86 anos. Sabendo que Raíssa é mais velha que Arthur 5 anos e a
que a idade de Raíssa somada com a idade de Teresa é igual a 83 anos, então podemos afirmar que Teresa
possui :
a) 75 anos
b) 70 anos
c) 65 anos
d) 60 anos
17) Valéria, Sônia, Edcarlos e Edvaldo com, 24, 47, 19 e 26 anos respectivamente, viajaram para Mariana
para voltar no mesmo dia para Ponte Nova. Ao chegar em Mariana, Edvaldo e Edcarlos resolveram ficar e
para aproveitar a carona, Patrícia, Solange e Raíssa, de 24, 47 e 8 anos, resolveram voltar para Ponte Nova.
Sabendo disso, podemos afirmar que a diferença das médias de idade na volta e na ida, respectivamente, dessa
viagem, é igual a:
a) 1 ano
b) 2 anos
c) 3 anos
d) 4 anos
18) Sabendo que
2 x 3 então x x 1 x 4 x 5 é igual a:
a) 4x-10
b) 10-4x
c) 8
d) 9
19) Renato tem hoje, 32 anos, idade que é o quádruplo da idade que Raíssa tinha quando Renato tinha o triplo
da idade que Raíssa tem hoje. Qual é a idade de Raíssa hoje?
a) 9 anos
b) 10 anos
c) 11 anos
d) 12 anos
20) Sabendo que o ângulo externo de um polígono regular de n lados é dado por
e
360
, então quantos
n
polígonos regulares tem a medida do seu ângulo interno dado por um número inteiro?
a) 24
b) 23
c) 22
d) 21
GABARITO MATEMÁTICA I:
1) A, 2) -, 3) A, 4) B, 5) B, 6) B, 7) C, 8) B, 9) C, 10) B, 11) B, 12) C, 13) D, 14) D
15) A, 16) A, 17) A, 18) C, 19) B, 20) C.
GABARITO MATEMÁTICA II:
1) E, 2) D, 3) B, 4) A, 5) E, 6) D, 7) C, 8) D, 9) B, 10) A, 11) B, 12) E, 13) D,
14) A, 15) B, 16) D, 17) C, 18) C, 19) B, 20) A, 21)B, 22) B, 23) A, 24) A, 25) B, 26) B, 27) D, 28) B.