LeisDeNewton_AtividadeComplementar

Plano de Estudos - Dinâmica - Leis de Newton
1. (Pucpr 1997)
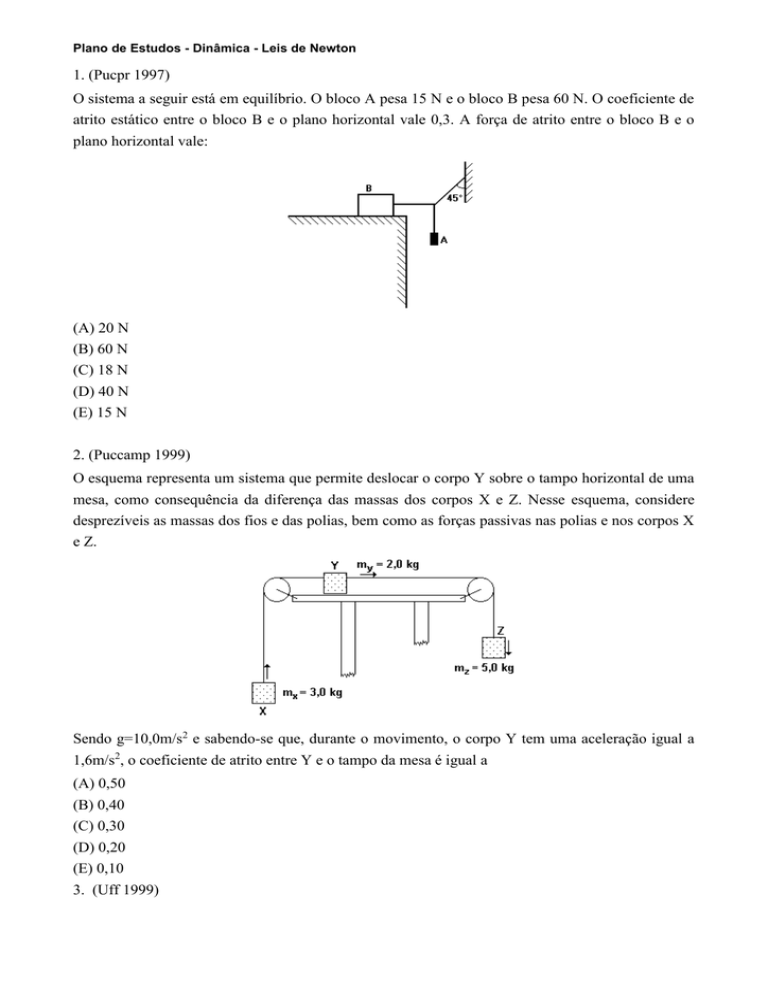
O sistema a seguir está em equilíbrio. O bloco A pesa 15 N e o bloco B pesa 60 N. O coeficiente de
atrito estático entre o bloco B e o plano horizontal vale 0,3. A força de atrito entre o bloco B e o
plano horizontal vale:
(A) 20 N
(B) 60 N
(C) 18 N
(D) 40 N
(E) 15 N
2. (Puccamp 1999)
O esquema representa um sistema que permite deslocar o corpo Y sobre o tampo horizontal de uma
mesa, como consequência da diferença das massas dos corpos X e Z. Nesse esquema, considere
desprezíveis as massas dos fios e das polias, bem como as forças passivas nas polias e nos corpos X
e Z.
Sendo g=10,0m/s2 e sabendo-se que, durante o movimento, o corpo Y tem uma aceleração igual a
1,6m/s2, o coeficiente de atrito entre Y e o tampo da mesa é igual a
(A) 0,50
(B) 0,40
(C) 0,30
(D) 0,20
(E) 0,10
3. (Uff 1999)
Plano de Estudos - Dinâmica - Leis de Newton
Uma caixa é puxada sobre um piso horizontal por uma força ( ), paralela ao piso, cujo módulo é
igual ao da força de atrito entre as superfícies em contato, com direção e sentido mostrados na
figura.
O gráfico velocidade (v) x tempo (t) que melhor descreve o movimento da caixa é:
4. (Fatec 2000)
Na figura a seguir, fios e polias são ideais. O objeto A de massa 10kg desce com aceleração
constante de 2,5m/s2, passando pelo ponto P com velocidade de 2m/s.
Adotando g = 10m/s2 e desprezando todas as forças de resistência, a massa do objeto B e a
velocidade com que o corpo A passa pelo ponto S são, respectivamente:
(A) 2,0 kg e 1,5 m/s
(B) 3,0 kg e 14 m/s
(C) 4,0 kg e 13 m/s
(D) 5,0 kg e 13 m/s.
(E) 6,0 kg e 12 m/s.
5. (Pucpr 2004)
Os corpos A e B de massas mA e mB, respectivamente, estão interligados por um fio que passa pela
Plano de Estudos - Dinâmica - Leis de Newton
polia, conforme a figura. A polia pode girar livremente em torno de seu eixo. A massa do fio e da
polia são considerados desprezíveis.
Se o sistema está em repouso é correto afirmar:
I. Se mA = mB, necessariamente existe atrito entre o corpo B e o plano inclinado.
II. Independente de existir ou não atrito entre o plano e o corpo B, deve-se ter mA = mB.
III. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente mA > mB.
IV. Se não existir atrito entre o corpo B e o plano inclinado, necessariamente mB > mA.
Está correta ou estão corretas:
(A) Somente I.
(B) Somente II .
(C) I e III.
(D) I e IV.
(E) Somente III.
6. (Fuvest 2006)
Uma esfera de massa m0 está pendurada por um fio, ligado em sua outra extremidade a um caixote,
de massa M=3 m0, sobre uma mesa horizontal. Quando o fio entre eles permanece não esticado e a
esfera é largada, após percorrer uma distância H0, ela atingirá uma velocidade V0, sem que o caixote
Plano de Estudos - Dinâmica - Leis de Newton
se mova. Na situação em que o fio entre eles estiver esticado, a esfera, puxando o caixote, após
percorrer a mesma distância H0, atingirá uma velocidade V igual a
(A)
V0
(B)
V0
(C) V0
(D) 2 V0
(E) 3 V0
7. (Unifesp 2006)
A figura representa um bloco B de massa mB apoiado sobre um plano horizontal e um bloco A de
massa mA a ele pendurado. O conjunto não se movimenta por causa do atrito entre o bloco B e o
plano, cujo coeficiente de atrito estático é μB.
Plano de Estudos - Dinâmica - Leis de Newton
Não leve em conta a massa do fio, considerado inextensível, nem o atrito no eixo da roldana. Sendo
g o módulo da aceleração da gravidade local, pode-se afirmar que o módulo da força de atrito
estático entre o bloco B e o plano
(A) é igual ao módulo do peso do bloco A.
(B) não tem relação alguma com o módulo do peso do bloco A.
(C) é igual ao produto mB . g . μB, mesmo que esse valor seja maior que o módulo do peso de A.
(D) é igual ao produto mB . g . μB, desde que esse valor seja menor que o módulo do peso de A.
(E) é igual ao módulo do peso do bloco B.
8. (Mackenzie 2008)
No sistema a seguir, o fio e a polia são considerados ideais e o atrito entre as superfícies em contato
é desprezível. Abandonando-se o corpo B a partir do repouso, no ponto M, verifica-se que, após 2 s,
ele passa pelo ponto N com velocidade de 8 m/s. Sabendo-se que a massa do corpo A é de 5 kg, a
massa do corpo B é
Plano de Estudos - Dinâmica - Leis de Newton
(A) 1 kg
(B) 2 kg
(C) 3 kg
(D) 4 kg
(E) 5 kg
Dados:
g = 10 m/s2
cos 37° = 0,8
sen 37° = 0,6
9. (Ufpb 2007)
Dois blocos A e B de massas mA = 6 kg e mB = 4 kg, respectivamente, estão apoiados sobre uma
mesa horizontal e movem-se sob a ação de uma força
F de módulo 60N, conforme representação na figura a
seguir.
Considere que o coeficiente de atrito dinâmico entre o
corpo A e a mesa é μA = 0,2 e que o coeficiente entre
Plano de Estudos - Dinâmica - Leis de Newton
o corpo B e a mesa é μB = 0,3. Com base nesses dados, o módulo da força exercida pelo bloco A
sobre o bloco B é:
(A) 26,4N
(B) 28,5N
(C) 32,4N
(D) 39,2N
(E) 48,4N
10. (Mackenzie 2009)
Um bloco A, de massa 6 kg, está preso a outro B, de massa 4 kg, por meio de uma mola ideal de
constante elástica 800 N/m. Os blocos estão apoiados sobre uma superfície horizontal e se
movimentam devido à ação da força
horizontal, de intensidade 60 N. Sendo o coeficiente de
atrito cinético entre as superfícies em contato igual a 0,4, a distensão da mola é de:
Dado: g = 10m/s2
(A) 3 cm
(B) 4 cm
(C) 5 cm
(D) 6 cm
(E) 7 cm
Gabarito:
Resposta da questao 1:
[E]
Resposta da questao 2:
[D]
Plano de Estudos - Dinâmica - Leis de Newton
Resposta da questao 3:
[A]
Resposta da questao 4:
[E]
Resposta da questao 5:
[D]
Resposta da questao 6:
[C]
Resposta da questao 7:
[A]
Resposta da questao 8:
[C]
Resposta da questao 9:
[A]
Resposta da questao 10:
[A]
Resolução
No Bloco A na direção horizontal e sentido da força F é verdadeiro escrever:
F(resultant(E) = m.a
F – F(elástic(A) – F(atrito) = m.a
F – k.x - μ.m.g = m.a
60 – 800.x – 0,4.6.10 = 6.a
60 – 800.x – 24 = 6.a
36 – 800.x = 6.a
No Bloco B nas mesmas condições já citadas
F(resultant(E) = m.a
F(elástic(A) – F(atrito) = m.a
k.x - μ.m.g = m.a
800.x – 0,4.4.10 = 4.a
800.x – 16 = 4.a
Resolvido, por adição, o sistema formado pelas duas equações
Plano de Estudos - Dinâmica - Leis de Newton
36 – 800.x = 6.a
800.x – 16 = 4.a
36 – 16 = 10.a
10.a = 20
E ainda: 800.x – 16 = 4.a
a=
= 2 m/s2
800.x = 16 + 4.2 = 16 + 8 = 24
x=
= 0,03 m = 3 cm